Structural health monitoring (SHM) is a rapidly evolving field, and there is a vast literature covering several topics that are related to this field. This entry is focused on the analysis of the state of the art of sensors for guided ultrasonic waves for the detection and localization of impacts for structural health monitoring (SHM).
- structural health monitoring (SHM)
- acoustic emission
- guided waves
- Lamb waves
- sensors
- ultrasound
- piezoelectric
- composites
- piezopolymers
- PVDF
- interdigital transducer (IDT)
- PWAS
- CMUT
- mems
- analog electronic front end
- analog signal processing
- impact localizati
1. Introduction
Structural health monitoring (SHM) is a rapidly evolving field, and there is a vast literature covering several topics that are related to this field, including several excellent reviews. The motivations of this paper are to report the recent developments on technologies, especially sensors and mixed signal electronic interfaces, which enable integration into a sensor node. The sensor node concept is analyzed in this review and the perspective for integrating with monitored facilities is examined. In the introduction the main concepts behind the design of a SHM system for impact monitoring and main review papers are reported. Later in the introduction, the main system components are defined and, in the following sections, they will be discussed more deeply.
Ultrasonic non-destructive investigation (NDI) methods that are based on the principle of acoustic emission (AE) have evolved over the past two decades towards structural monitoring systems with guided ultrasonic waves [1,2], driven by applications in the aerospace, civil engineering, energy conversion, and transportation systems automotive (e.g., wind turbines, pipelines, and liquid natural gas cylinders). The safety of the structure and the prediction of in-service period are the key elements that must be provided by SHM and the underlying theory about these topics were explained in a comprehensive work by Farrar and Worden [3] and in a related book [4]. Structure damaging can occur for different causes (e.g., breakages due to fatigue, mechanical and thermal stresses, impacts with objects, etc.), and their consequences often are not optically visible or detectable. The damage is sometimes not visible, because it is internal to the structure or small but not without importance from the point of view of the safety and reliability of the operation of the system. To avoid catastrophic accidents, the damage prognosis is an essential task that is connected to the impact events; a framework for the damage prognosis was described in chapter 14 of the book that was published by Farrar and Worden [5].
Non-Destructive Testing (NDT) is a wide group of analysis techniques used in science and technology industry to evaluate the properties of a material, component, or system without causing damage, and it is often carried out in laboratory or on site on a scheduled program. SHM, unlike NDT, requires the installation of sensors/transducers operating in the environment in which the structure operates under remote control and for this reason the realization of such systems requires a considerable effort of integration of several disciplines:
-
(1)
-
modelling of damage physical phenomena and their influence on the physical sensed quantities,
-
(2)
-
sensors, including calibration and self-diagnostics,
-
(3)
-
front-end electronics including embedded processing,
-
(4)
-
data transmission (wired, wireless),
-
(5)
-
online (or real time) or offline signal/image processing,
-
(6)
-
impact event detection and localization
-
(7)
-
damage detection and classification techniques that are based on database processing,
-
(8)
-
prognostics,
-
(9)
-
artificial intelligence (AI)/machine learning (ML) for automatic damage detection and progression evaluation.
Figure 1 illustrates the different components of an SHM system and their interaction: the environmental conditions, the on-site hardware, and the off-site hardware and software resources. The different characteristics of the structures (dimensions, materials, and environmental conditions) and their structural monitoring systems (cost, footprint, weight, power consumption, safety and reliability criteria, and response/update times) often require the design of ad hoc systems by exploiting multidisciplinary knowledge in electronics, informatics, telecommunications, and, finally, material technology and mechanical properties.
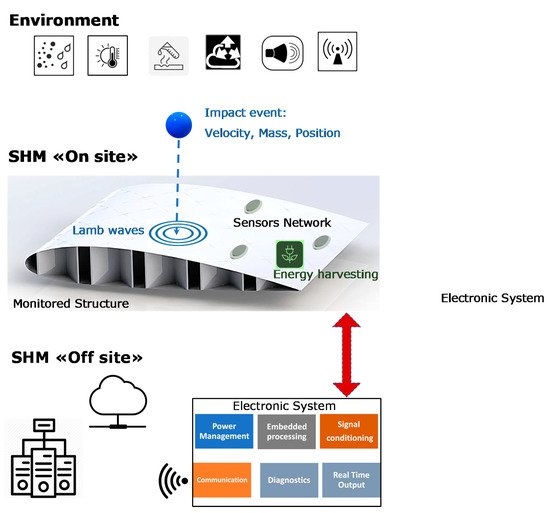
Figure 1. Graphical representation of an advanced structural health monitoring (SHM) system for impact monitoring. (Top) Environmental conditions (dust, moisture, temperature, pressure, vibrations, electromagnetic interference) and impact events characterized by the object mass, velocity, shape and dimensions. (Centre) On-site components of the SHM system subjected to environment conditions installed on the monitored structure (e.g., a section of a composite airplane wing). (Bottom) Off-site components installed remotely and connected to the sensors network; the Electronic System can operate in a protected environment (e.g., inside airplane fuselage) with real-time processing capability. Off-line signal/data processing based on big data archive with workstations connected to the web for software applications of Artificial Intelligence/Machine Learning (AI/ML) and prognostics.
For a general understanding of the state of the art, the reader can refer to the review paper of Mitra et al. [6], where several publications relating to the various components of an SHM system are discussed (see Figure 1); in the paper of Mitra et al. [6], various monitoring techniques based on ultrasonic guided waves (UGW) piezoelectric and fiber optic sensors, laser vibrometry (SLDV) techniques are examined. In addition, indications are given of what research and development lines may be for advanced SHM systems. As already introduced in this paragraph, monitoring techniques that are based on UGW by piezoelectric transducers are among the most common and most developed, since they have a longer history [7] than SHM systems based on optical sensors, in particular Fiber Bragg Grating (FBG) sensors; for completeness, the evolution of state of the art for optoelectronic sensors is reported in [8,9,10,11,12], but it is not discussed further in this paper. Similarly, the evolution of piezoelectric materials for the construction of UGW sensors and transducers, the development of low-power consumption integrated electronic components and systems requires a continuous updating of research to provide new design methodologies and technologies to bring in the field the SHM systems. Although many published papers report the outcomes that were obtained with laboratory set-up of guided ultrasonic wave SHM systems, their demonstration in the field is still limited. For the latter problem, there are various reasons, but certainly one of these is the complexity of the installation of the sensors on a target structure, the real time signal acquisition and processing, and the replication of the real-life environmental conditions. An interesting reference for the testing of SHM systems in the aerospace industry is provided in a report that was presented by Dennis Roach of Sandia National Labs [13]: this report shows the objectives and implementations of SHM systems for airplanes and includes several examples with piezoelectric and fiber optic sensor applications for monitoring impacts, deformations, debonding, delamination, and damage progression.
Finally, it is useful to point out the effort made to create standards for the development of systems and methods for SHM and NDT based on acoustic emission, especially for the rapidly evolving SHM sector; a comprehensive reference is the British Standard for Acoustic Emission and Condition Monitoring that was published in The Official Yearbook of the British Institute of Non-Destructive Testing [14]. Some main book references on SHM based on UGW can be found in [15,16,17,18,19]. After this introduction of the background of SHM systems that are based on UGW in active and passive modes, the present paper focusses the elements of the system that is shown in Figure 1 for the implementation of impact monitoring advanced systems on metal and composite materials with UGW piezoelectric sensors. In this paper, we primarily consider piezoelectric sensors used for impact detection in passive (“listening”) mode, but also in combination with the transducers operating in active mode for the investigation of damage and its progression over time. The trend of integrating different sensor types (UGW, FBG, accelerometer, strain, temperature, etc.) into a node increases the information regarding the impact and the operational conditions of the sensors that are influenced by the environment, leading to the concept of a “multifunctional sensor node”.
The evolution from the common AE monitoring configuration with a layout of sparse single element sensors with off-the shelf electronics to the recent design of sensors networks with “smart-sensor nodes” requires a continuous analysis and evaluation of the progresses in several fields.
2. Characteristics of Signals Generated by Impacts on Planar Structures Relevant to the Design of SHM Systems
2.1. Dispersion and Attenuation of Lamb Waves
In this section, the implication of the attenuation and dispersion characteristics of UGW relevant for the design and implementation of a SHM system are discussed. The interested reader can find main references for the theory and modelling of ultrasonic guided waves [1,20]. In brief, we point out that ultrasonic waves that are guided for SHM are mechanical waves that propagate within a material delimited by an interface with a different medium. Propagation within the space-limited structure simultaneously produces dispersive modes of propagation in frequency. In the case of structures with thicknesses comparable to wavelength, such as thin planar structures, propagation modes have symmetrical and antisymmetric characteristics with respect to the axis of symmetry of the structure and they are determined by the theory behind Lamb waves, as explained in [21]. For an isotropic and homogeneous laminate material (e.g., aluminum), we illustrate the dispersion characteristics in Figure 2 (top) by the calculated phase velocities for the different guided modes versus the frequency x thickness product (fxd). Another difference between these two UGW modes is the dependence on frequency attenuation, as shown in Figure 2 (bottom): the S0 mode is remarkably attenuated in the low frequency range and for the reception of this mode is necessary a high pass filtering and amplifier gain to be separated from the slower and higher amplitude components of the A0 mode.
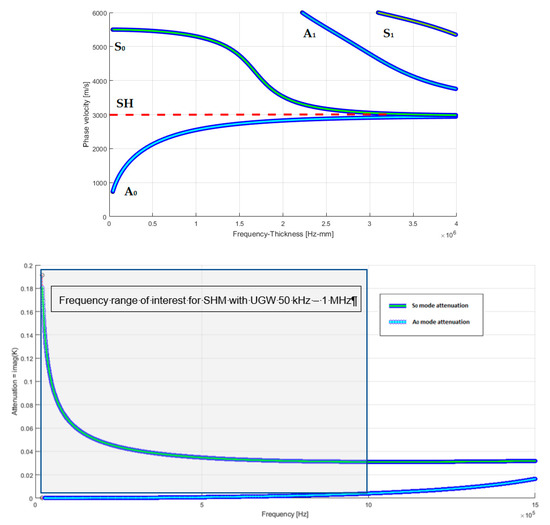
Therefore, the propagation of symmetrical modes within a planar structure is a two-dimensional phenomenon; the propagation of the various modes is subjected to attenuation that mainly follows the law of geometric decay inversely at the root of the distance. The authors in [20] proposed a deep and comprehensive analysis of the attenuation phenomena that are basic in differentiating the design of SHM systems according to the characteristics of the different materials (composite or metallic) and the size of the structure; thus, attenuation analysis is essential in defining the distance and area coverage with a certain type of transducer/sensor without exceeding the attenuation limit (50–70 dB), which results in being difficult to deal with analog-front-end (AFE) electronics based on COTS, unless it has an acceptably expensive and complex electronic customized design. Indicatively, the operating frequencies for Lamb’s guided ultrasonic waves range from 100 kHz to 1 MHz and, in this wide range, a compromise must be found between attenuation, wavelength, minimum detectable impact energy, and for the transducers/sensors, the size, type, sensitivity, and bandwidth. To solve these problems, methods for optimizing the position of transducers have recently been proposed by Mallardo et al. [22] based on the background of UGW propagation theory; in this work, a method is developed to define the optimal positions considering the characteristics of the material and sensors, thus also optimizing the number of sensors transducers, while concluding that there is no general solution to the problem, since each application has different constraints and, therefore, requires a series of a priori choices.
2.2. Ultrasonic Guided Waves Generated by Different Velocity of Impacts on Isotropic Elastic Plates
Impact monitoring systems can be designed for different applications, where impacts with different objects hitting the structure have different energy, mass, and velocity. It is of interest to explain the different effects on UGWs that were generated by impacts at different velocity. There are several categories of impact loading: low velocity (large mass), intermediate velocity, high/ballistic velocity (small mass), and hyper velocity impacts. These categories of impact loading are important because there are remarkable differences in energy transfer between the object and target, energy dissipation, and damage propagation mechanisms as the velocity of the object varies. Low velocity impacts occur typically at a velocity below 10 m/s, intermediate impacts occur between 10 m/s and 50 m/s, high velocity (ballistic) impacts have a range of velocity from 50 m/s to 1000 m/s, and hyper velocity impacts have the range of 2 km/s to 5 km/s, according to the literature [23].
In several studies [19,20,21], the signals generated by non-destructive impacts have been treated, which is impacts that do not cause any damage to the laminate under examination. These papers consider single and multiple impacts, but detailed information on the energy characteristics is not provided regarding the impacts analyzed. Furthermore, in [22], the impacts are distinguished based on the potential energy of the impacting bodies, with values ranging from 500 mJ to 3.5 mJ. In other early studies on this subject [23,24], the impacts are instead distinguished based on the impact velocity. In several studies [24,25,26], signals that are generated by non-destructive impacts have been treated, which is, they do not cause any damage to the laminate under examination, neither with single impact nor with multiple impacts, however no information is given on the extent of impact. Furthermore, in [27], the impacts are distinguished based on the potential energy of the impacting bodies, with values ranging from 500 mJ to 3.5 mJ. In other early studies on this subject [28,29], the impacts are instead distinguished based on the impact velocity.
The study of impacts that occur in an isotropic elastic flat plate is based on following assumptions:
According to the above assumptions, we can remark that the main feature of the signals generated by impacts is the impact velocity that also determines the amplitude of the Lamb waves. From the physics laws for a falling body from a certain height, the potential energy is converted to kinetic energy; the impact velocity vi can be calculated by knowing the kinetic energy Ek and the mass m of the impacting object, as reported in the following formula:
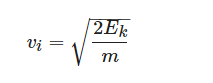
The study reported in [28] shows that two fundamental propagation modes can be distinguished in impact phenomena: a slow propagation mode (flexural mode or A0 mode) and a fast propagation mode (extensional mode or S0 mode).
The amplitude of the signal in A0 mode is dominant as compared to the S0 mode, but the amplitude of the latter is strongly linked to the speed of the impact: the greater the speed of the impact the greater the amplitude of the signal relative to the S0 mode. The authors in [28] also reported an acquired signal from a high-speed impact (700 m/s), where they demonstrate, when that applying a low-pass filter with (with a cut-off frequency of 800 kHz), it is possible to only extract the two fundamental propagation modes (A0 and S0) and, in this case, the amplitude of the S0 mode becomes comparable to that of the A0 mode. According to the authors experience, we investigated the possibility to also extract the S0 mode signal in low velocity impacts by applying a low-pass filter in the analogic front-end electronic board with proper cut-off frequency. Figure 3 shows ultrasonic signals that are generated by a low-velocity impact (about 3 m/s) on an aluminum plate with thickness 1.5 mm.
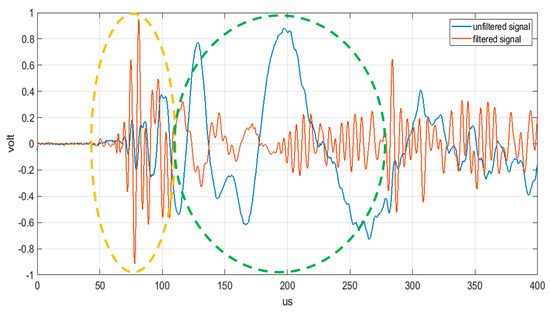
Figure 3. Ultrasonic signals generated by a low-velocity impact (about 3 m/s) in blue color, and the same signal filtered by an analogic low-pass filter with a cut-off frequency of 400 kHz in red color. The dotted green circle represents the portion of the signal relative to the A0 mode; the dotted yellow circle represents the portion of the signal relative to the S0 mode.
From the analysis of Figure 3, it is apparent that the fast propagation mode S0 becomes comparable in amplitude with the A0 mode only after filtering the ultrasonic propagating signal that is generated by the impact. The possibility of processing the fast S0 mode instead of the slower A0 mode, is often the best signal processing design strategy, because this early arrival time signal is less affected by overlapping of the multiple reflections from the structure edges [33]; moreover, the impact signal detection and positioning is even more complicated in large structures for the higher attenuation and the mode conversions after the propagation on areas with different thicknesses. The topics briefly reviewed in this section remark the importance of the understanding the physical background for designing sensors and the analog front-end to simplify and make the information extraction from the signal reliable.
2.3. Signal Processing Techniques for Dispersion and Environmental Factors Compensation
From the preliminary considerations in the Introduction, we can remark that the rapid evolution towards integrated-SHM (ISHM) systems operating in different environmental conditions follows a different path than the common AE and NDT techniques, which use volumetric longitudinal or transverse ultrasonic waves with piezoelectric transducers that are connected to portable instruments and the region of interest (ROI) manually scanned of by a trained operator [34]; main differences are found for the signal processing adopted for both passive and active mode operation of the SHM system. The analysis of information gathered by a sensors layout due to the interaction between the UGW dispersive modes and the various types of structures is certainly a challenging aspect from the point of view of signal processing techniques that are based on the Continuous Wavelet Transform (CWT) or the Short Time Fourier transform (STFT). CWT decomposes a time domain signal into components that correspond to a frequency band. Each of these components contains a further temporal discretization. The resolution of the temporal discretization varies with each frequency component, resulting in a multi-resolution temporal frequency analysis. Because the modes S0 and A0 propagate with different amplitudes in the useful band and with different propagation speeds (see Figure 2), the CWT allows for a representation capable of separating the two contributions in different instants of time. One of the limitations of the CWT is the compromise between resolution in frequency and in time and, moreover, the calculation algorithm requires considerable computational resources, not always available within a sensor node. Alternatively, the simplest form is represented by the STFT, but, differently from CWT, does not have the possibility to be implemented with the multi-resolution functionality in the time/frequency domain. For example, the separation of the two modes S0 and A0 by CWT o STFT is relevant for the evaluation of the DToAs for low and high velocity impacts, as we will describe in Section 2.2. However, simple analysis with CWT or STFT may still be too restrictive in the presence of structures with inserts, reinforcement elements, and therefore several methods have recently been proposed to overcome this problem, such as those reported in [30,31,32,35,36,37]. The well-known time-reversal approachis another important method introduced in [38] to compensate for the dispersion and alleviate the complexity of Lamb wave signal interpretation; this approach was adopted by Zeng et al. [39]. The dispersion of the generated modes by impacts influences the spatial resolution of the adopted localization algorithm, because the propagation on long distances (e.g., meters) [40] on the plate elongates the initial wavelet. The mitigation of this problem can be done using algorithms that can process the received signals by compensating the phase delay according to the theory of UGW [1]. There are available efficient algorithms for this task, such as multiple signal classification (MUSIC) and RAPID [41]. New developments that are based on the MUSIC algorithm have been proposed for impact energy estimation [42] and for the direction of arrival of a Lamb wave [43]. The computational efficiency is also important for real-time systems and Zhong et al. proposed an improvement in the processing scheme [44].
The UGWs used in active mode for damage assessment have a great sensitivity to detect internal damage into the structure, and this is one of the main reasons of successful application of this NDT technique. The detection is often implemented on a data driven approach, where the received UGWs from a sensor layout are compared with a baseline of data acquired with a pristine structure. This approach is also rather simple to implement in sensors with on board embedded processing, but it suffers from the sensitivity to environmental and operational conditions, mainly temperature variations. Recently, Mariani et al. [45,46] have proposed a method for the compensation of this detrimental phenomenon. For the electro-mechanical-impedance (EMI) method, the temperature compensation was achieved with some benefits by using artificial neural network (ANN) as reported by Sepehry et al. [47].
2.4. Advanced Methods for Impact Detection and Localization
In general, impacts on a thin planar structure generate guided waves modes that can propagate away from the impact point. The localization of the impact point is commonly achieved by adopting a triangulation algorithm with at least three passive ultrasonic sensors being deployed on the planar structure. The accuracy of the impact point estimation depends on the estimates of the guided modes velocity and the measured differential time of arrival (DToA) among the sensors [48]. Recently, several papers have been published to improve the reliability and accuracy of impacts on complex structures other than from the simple panels often used by researchers in laboratory for calibration and performance assessment of a SHM system. The Akaike Information Criterion (AIC) criterion for the accurate estimation of DToA has been demonstrated by De Simone et al. [49]. Further research work has consolidated the investigation of the advantages of AIC, and a modified version for impact monitoring has been recently proposed by Seno et al. [50]. In the latter work, an ANN was trained for automatic classification of defects in composite materials that were tested in laboratory and simulated operational conditions. As already reported in the Introduction, Ono reports an extensive review of AE physical parameters for SHM systems in [20]. The characteristic of UGW generated by impacts has been outlined in Section 2.1 and Section 2.2. Such guided wave modes propagating into the planar structure mix-up due to the phase velocity dispersion and, in addition, the reflection phenomenon from the edge or from inserts or stiffening material or defects [51]. Moreover, mode conversion can occur when the ultrasonic guided waves travel across a discontinuity of acoustic properties in the planar structure, for example, a change in thickness or material composition. In general, the wave shape of the impact generated UGW is complex, but a list of features supported by theoretical modelling developed by Hakoda et al. [52] based on the phase velocity analysis can be derived. It is worth noticing that the propagation velocity analysis, in general, is more complex for a composite three-dimensional structure than the simpler case shown in Figure 2; even the example of time domain signals generated on an aluminum plate reported in Figure 3 is a simplified scenario with respect to real-life cases. In the following, we report two main considerations that are starting guidelines for the impact signals processing:
- (1)
-
the early part of the signal consists of the fast phase velocity modes, typically the S0 mode in the low frequency range below the cut off frequency × thickness product (e.g., equal to 1.5 MHz × mm in Figure 2).
-
(2)
-
in the later part of the signal the contribution comes from slower modes that show also dispersion effect as for the A0 mode [53] or signals that travelled along longer paths or multiple reflections.
We can observe that the S0 mode being faster than A0 it is less prone to being overlapped by delayed signals, but, due to the greater attenuation at low frequencies, the S0 mode has a lower amplitude than the A0 mode; the higher velocity of this mode also implies that the error on its DToA estimation causes higher spatial errors in the triangulation algorithms or any other positioning method based on DToA [54,55,56]. The theory of UGW in a plate like structure also considers other types of waves than Symmetrical and Antisymmetrical Lamb wave modes: the shear horizontal (SH) mode. This is a non-dispersive mode and piezoelectric sensors/transducers can be designed to convert this wave type into voltage signals. Ren and Lisseden [57] have demonstrated the capability of also sensing Lamb waves that are of interest for impact detection in passive mode. Altammar et al. [58] studied the actuation and reception of shear modes by exploiting the d35 piezoelectric coefficient of lead zirconate titanate (PZT) sensors that were embedded in a laminate structure. d35 PZT is a class of PZT piezoelectric transducers that, when polarized along their thickness, they induce shear strain in the piezoelectric material. It is interesting to observe that the shear deformation has a stronger coupling coefficient (d35) than the common d33 or d31, indicating that d35 PZTs have stronger electromechanical coupling for sensing and actuation.
In the final part of this section, we review the advancements on signal processing techniques for anisotropic plate-like material. Anisotropic characteristics of composite structure require the adaption of impact positioning algorithms that were developed for isotropic plate like materials. The early research on signal processing techniques for isotropic metallic plates and anisotropic composites can be found in [26,56,59,60]. More recently, the signal processing techniques have been progressed to account for the UGW dispersion (see Section 2.1) and anisotropy of different type of composites, like unidirectional, quasi-isotropic composite fiber reinforce polymer (CFRP), and honeycomb, which are of interest for aerospace industry [39,49,56,61,62]. An early work of Scholey and Wilcox in 2010 [63] addressed the problem of impact detection on 3D structures and, recently, Moron et al. in 2015 [64]. Lanza di Scalea et al. published a work [65] for impact monitoring in complex composite material structure with an algorithm that is based on the rosette sensor configuration; this model-based approach could solve the problem of variation of phase velocity along different direction of a composite material.
3. Hardware Developments of Wired and Wireless Sensor Networks (WSNs) for SHM and Validation Tests
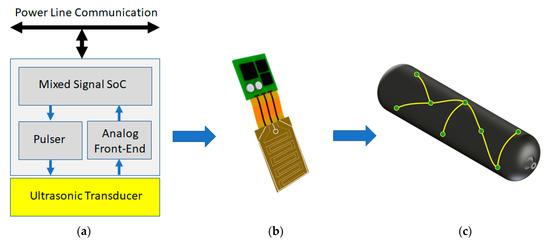
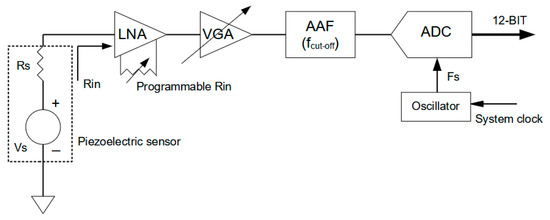
3.1. Nodes and Modules with Low Power Electronics Solutions with Energy Harvesting

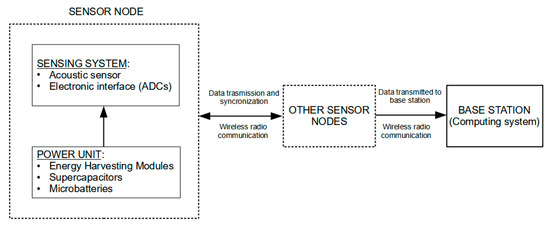
3.2. Toward SHM Sensor Networks with Smart Nodes
3.3. WSN and IoT for SHM
-
Sensing and data Acquisition Subsystem.
-
Data Management Subsystem: preprocessing methods used to organize raw data that were acquired from sensors and remove the noise before processing; novelty detection, classification, and regression approaches. Among them, novelty detection based on artificial neural networks.
-
Data Access and Retrieval Subsystem.
This entry is adapted from the peer-reviewed paper 10.3390/s21092929
