Packaging Materials: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Materials Science, Ceramics
Contributor:
Qingshan Duan

The entry packaging materials is intended to summarize the recent progress in the work of fractal theory in packaging material to provide important insights into applied research on fractal in packaging materials. The fractal analysis methods employed for inorganic materials such as metal alloys and ceramics, polymers, and their composites are reviewed from the aspects of fractal feature extraction and fractal dimension calculation methods. Through the fractal dimension of packaging materials and the fractal in their preparation process, the relationship between the fractal characteristic parameters and the properties of packaging materials is discussed. The fractal analysis method can qualitatively and quantitatively characterize the fractal characteristics, microstructure, and properties of a large number of various types of packaging materials. 

  • fractal theory
  • fractal dimension
  • packaging materials

1. Introduction

Mandelbrot proposed the concept of fractal in 1975, which refers to the graph, phenomenon, or process with self-similarity [1]. Fractal objects generally exist in nature, such as curved coastline, rough surface, and so on [2][3]. At present, fractal theory has been extensively used in natural science, engineering technology, social culture, and other fields [4][5][6][7]. In the packaging industry, the surface morphologies of all kinds of packaging materials are complex and irregular, but they have features of self-similarity, which is highly appropriate for analysis by fractal theory. Many scholars have been using fractal theory to compute the fractal dimension of packaging materials and build the relationship between the properties of packaging materials and fractal dimension. As is known to all, a lot of materials can be availed in the packaging industry, so packaging materials involve a wide range of materials. In order to ensure people have a comprehensive and in-depth understanding of the fractal in a variety of packaging materials, it is necessary to summarize and sort out the application progress of fractal theory in the research of packaging materials, to promote the development of fractal theory in the research of packaging materials.

2. Properties and Fractal of Polymers and Their Composites in the Packaging Field

Polymers and their composites are widely used in the field of packaging materials, including plant fiber, petroleum-based, and bio-based polymer materials, and composite materials with the above components. In this section, the research statuses of fractal characteristics, material preparation and properties, and fractal dimension models of various types of materials are reviewed.

2.1. Fractal in the Preparation of Polymers and Their Composites in the Packaging Field

In the preparation process of polymers and their composites, the preparation environment, and the formation of crystals and aggregates have fractal characteristics. For obtaining the relationship between gas-liquid interfacial tension and its fractal dimension, Wang et al. [8] put forward a method to calculate the fractal dimension of gas-liquid interface. In the suspension, the fractal dimension of different systems is different; under shear, the suspension structure may be more inclined to reaction limited cluster-cluster aggregation(RLCA), and a more flocculated structure or particle rearrangement may exist in the suspension, which can result in a dense filler structure in the shear suspension structure [9]. As for the nanoparticles doped in polymer materials, the diffusion of nanoparticles in fractal interior and surface determines the shape of islands left on the surface after fractal fragmentation [10]. Santillán et al. [11] reported the self-assembled fractal structure of spherical Ag nanoparticles (NPS) prepared in water, such as Figure 1. In the prepared colloidal suspension, the fractal aggregates with size of about 31 nm were observed, as shown in Figure 2. In order to understand the growth mechanism of nano agglomerates and reveal the correlation between microstructure and macroscopic properties, Liu et al. [12] tested and analyzed the multifractal structures of pure polyimide (PI) film and inorganic nano hybrid PI film, and studied the spatial distribution and mass uniformity of the scatterers.

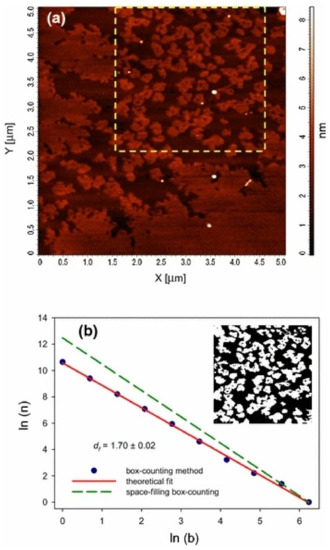
Materials 14 00860 g006 550

Figure 1. An AFM image (a) and its fractal dimension (b) of a rosette-shaped fractal structure limited by a plain region.

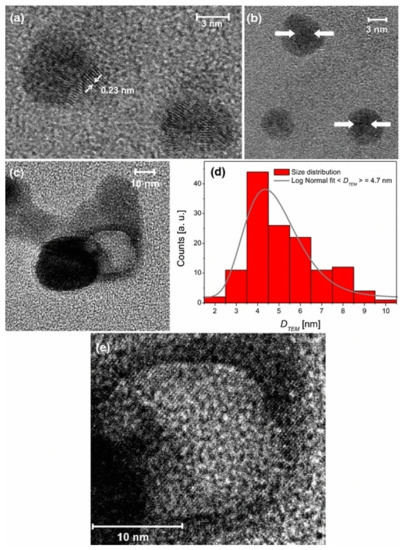
Materials 14 00860 g007 550

Figure 2. TEM images of Nps present in the colloidal suspension generated by femtosecond laser ablation: (a) isolated silver bare core Nps, (b) isolated silver core–shell Nps, (c) hollow metal Np together with a bare core Np, (d) size histogram obtained by measuring 140 particles within the sample and log-normal fit curve, and (e) enlargement of panel c where Bragg planes in the central zone of the hollow Np can be seen.

The materials prepared by self-assembly technology have fractal characteristics. In the process of preparing layer-by-layer self-assembled antibacterial films of hyaluronic acid (HA) and chitosan (CHI) biopolymers at two pH values (5 and 3), the fractal dimension of the pH 5 series was about 2.2, and the irregularity of the initial random adsorption process was the least. When the pH value was reduced to 3, the fractal dimension increased to 2.5, indicating that the random adsorption process was in the transition of diffusion limited aggregation [12]. In the electrospinning process, the length of the electrospinning needle is controlled to realize the structural control of materials at the molecular scale, which shows that the hierarchical structure of macromolecules in the self-assembly process has fractal characteristics [13]. Fractal patterns can be formed in the process of chemical deposition; the main factors affecting the formation rate and final geometry of aggregation fractal patterns are the molecular weight of polymers, the selection of reaction electrodes, and air exposure [14].

To sum up, in the preparation of polymers and their composites in the packaging field, we can analyze and predict the properties of materials via the fractal characteristics of diffusion of nano-particles in polymer materials, the growth mechanism of nano aggregates in solution systems, and the fractal characteristics of self-assembly technology, so as to obtain ideal polymer materials and their composites for packaging. At the same time, the self-assembly technology forming fractal pattern can be applied to obtain an ideal material surface.

2.2. Fractal Characteristics and Fractal Dimension of Polymers and Their Composites in the Packaging Field

Searching for the characteristics and laws of polymer and their composites surface and component dispersion, numerous studies use different methods to characterize fractal characteristics and fractal dimensions. Using a microscope, Ritter et al. [15] discovered that the growth of cyclic fatigue crack in the epoxy resin/glass interface region presented viscosity and fractal. Nie et al. [16] calculated the fractal dimension of TEM images of SiO2/acrylate composites, and found that the closer the fractal dimension is to 2, the better the dispersion uniformity of the dispersed phase is. Zhang et al. [17] found that the longitudinal shear strength of wood has a positive correlation with the fractal dimension of fracture surface, while transverse shear strength has a linear positive correlation with it. For studying the relationship between interfacial adhesion and preparation technology, Nano calcium carbonate impregnation modification (IM) is employed as an effective way to improve the interface interaction of the bamboo fiber reinforced HDPE composites. Fractal theory and dynamic mechanics were used to analyze the composites produced by three processes: extrusion (EMP), injection molding (IMP), and hot pressing (HPMP). The binary pictures of composites fracture surface for EMP, IMP, and HPMP were diverse (Figure 3), and the surface fractal dimension of the three types were different; EMP composites needed the least potential energy to change the structure, the interfacial adhesion of EMP composites was the best, while the HPMP composite was the worst [18].

Materials 14 00860 g008 550

Figure 3. Binary pictures of composites fracture surface for EMP (a), IMP (b), and HPMP (c).

The fractal dimension of AFM images describing the characteristic structure of z-scale factors can reflect the fractal characteristics of materials more comprehensively than the fractal dimension obtained by roughness [19]. Gabibov et al. [20] found that the composite structure composed of styrene butadiene rubber (SBR) and epoxy resin ED-20 filled with nanoparticles is a combination of two fractals. The “disturbance” of polymer matrix structure caused by filler particles depends on the concentration and size of the initial filler particles; they found that the fractal dimension of the aggregate surface of the initial filler particles affects the fractal dimension and size of the filler particles; the particle size and aggregation parameters grow; and the fractal dimension of particle aggregates increases.

In summary, the application of the fractal dimension of the z-scale factor characteristic structure in the AFM image can more fully reflect the fractal characteristics of the material surface. This parameter may help better analyze the material properties, which may be a direction that subsequent researchers need to pay attention to.

2.3. Relationship between Fractal Dimension and Properties of Polymers and Their Composites in the Packaging Industry

With the development of fractal theory and material properties, people are more inclined to figure out the relationship between the fractal dimension and properties of polymers and their composites. In recent years, research on the fractal dimension and properties of packaging paper, natural plant fiber, petroleum-based polymer and their composites, nano materials, and porous materials in the packaging industry mainly comprise the following aspects:

With regard to packaging paper and natural plant fiber, SEM and TEM are usually used to acquire surface morphology, and fractal theory can also be applied for analysis. The surface of food packaging paper was scanned by SEM, and surface porosity was analyzed according to fractal theory [21]. Campano et al. [22] investigated the bulk morphology of CNCs and CNFs by TEM, and quantified the aggregation/dispersion degree and fibrillation degree of CNFs by fractal dimension and porosity, as shown in Figure 4.

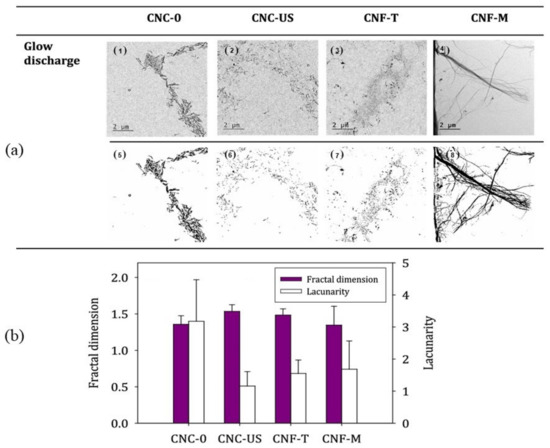
Materials 14 00860 g009 550

Figure 4. TEM images (a) (pretreated through glow discharge (subfigures 1–4) and processed images (subfigures 5–8)) and fractal dimension (b) of CNCs and CNFs samples.

The properties of other polymers and their complex materials in the packaging industry was researched by the fractal dimension. Dispersion of reduced graphene oxide within thermoplastic starch/poly (lactic acid) blends was investigated by small-angle X-ray scattering; the formation of a fractal structure led to the significant enhancement of macroscopic properties [23]. In sustainable biocomposites from Nylon 6 and polypropylene blends and biocarbon, angular particles having a high polydispersity and porosity were shown to form pendular and funicular morphologies when compounded in immiscible blends, and their morphology could be distinguished by fractal dimension; the mechanical properties of the composite are better than that of the original [24]. The fractal characteristics of impact fracture surface of bamboo plastic composite with core shell structure were analyzed by the box counting dimension method, the surface fractal dimension was in the range of 2.2075–2.2204, the relationship between the impact strength and the fractal dimension of fracture surface was an approximate power exponent, indicating that the surface fractal dimension of fracture could reflect the impact strength of core-shell structure bamboo plastic composite [25]. Fractal characteristics of the impact strength of polypropylene/polypropylene grafted maleic anhydride/potassium hexatitanate whisker (PP/PP-g-MAH/SPTW) composite packaging materials were studied by box counting method using FractalFox software, the fractal dimension of cross-section was in the range of 1.4165–1.8832, and the impact strength of PP/PP-g-MAH/SPTW was positively correlated with the power exponent of fractal dimension [26]. The fractal dimension of tensile section of polypropylene/fly ash composite filled with the silicon carbide whiskers was computed by the differential box counting method from 1.24 to 1.90, and the logarithm of tensile strength has a linear function relationship with its fractal dimension [27]. Lu et al. [28] found that with the increase of nano AlN content, the microcrack fractal dimension of nano AlN/PTFE composite increases. The larger the fractal dimension of microcracks, the more disordered the distribution of microcracks on the material surface, which is conducive to the formation of a transfer film on the dual surface of the composite material, and helps to improve wear resistance; the greater the fractal dimension of microcracks, the more disordered the distribution of microcracks on the surface of materials, the tensile fracture of materials gradually changes from ductile fracture to brittle fracture, resulting in the decrease of tensile properties of materials. The effect of fractal dimension and branch number on thermal conductivity of Si/Ge nanocomposites with fractal tree network was studied by the molecular dynamics simulation method, the Si/Ge nanocomposites with fractal tree network had greater length and width, fractal dimension and more branch layers than other Si/Ge nanocomposites; the sub interface scattering is stronger, and the fractal tree network is better than the traditional rectangular core structure in reducing the thermal conductivity of nanocomposites [29]. The structural stability and properties of the dispersed filled polymer were analyzed by using the macro structure image processing results based on the texture method and multifractal method [30]. Wu et al. [31] prepared glass bead/polypropylene (GB/PP) composite by the melt blending method, observed the dispersion morphology of GB in the cross-section of the composite by SEM, and calculated the dispersion fractal dimension (Dd) of GB by fractal model. The results demonstrated that Dd can quantitatively characterize the dispersion effect of GB; the larger the Dd, the more uniform the dispersion of GB, the higher the impact strength and toughness of the composites.

For the fractal structure, the second moment of particles in composites is expressed as < r 2 t > ∝ t 2 α , where α is Hurst index, which can reflect the diffusion law of particles. When Hurst index is greater than 0.5, it is part of accelerated diffusion; when it is 0.5, it is free diffusion; when it is less than 0.5, it pertains to secondary diffusion, and diffusion is slow. Qu et al. [32] obtained the diffusion law of particles in fractal structure by numerical simulation and comparison of Hurst index and its influencing factors in the condition that particles cannot enter the matrix and can move in the matrix and gap at the same time. Jelcic et al. [33] found that the average fractal index of the fracture surface of the binary elastomer of impact resistant polystyrene (HIPS) and polystyrene-b-polybutadiene-b-polystyrene block copolymer (SBS) is less than 2, and the fractal results are related to the mechanical properties of the blends and the Hurst index obtained from the time series of processing parameters (e.g., torque and melt pressure). Moreover, for the heterogeneous polymer blends, the processing and mechanical results agree with the fractal characteristics of the fracture surface [34].

Apart from the earlier calculation method of fractal dimension of graphics, the signal fractal dimension calculation method is also applied to the performance analysis of composite materials. Based on the non-stationary AE signals in tensile and bending tests of glass fiber reinforced polymer matrix composites, the Hurst index, the scaling index of DFA analysis method, the minimum covering dimension and the box counting dimension of the AE signal were calculated when matrix cracking, fiber/matrix peeling, delamination, and fiber fracture were occurred; the foregoing indicators can distinguish different failure mechanisms; the AE signal of the product has multifractal behavior [35].

Porous materials with low relative density, large specific strength, and specific surface area have been widely concerned in the field of packaging material. The preparation and properties of porous materials are one of the key focuses in the field of packaging materials. Compared with other packaging materials, the fractal research of porous polymer materials for packaging is more in-depth and detailed, including fractal dimension, mechanical properties of porous materials, adsorption and seepage process, and property relationship. Zhang et al. [36] obtained the pressure (p) and mercury injection (V) of Aramid paper-based materials by MIP, and then calculate the slope of ln(dV/dp)-lnp curve, namely, the fractal dimension. The fractal dimension was positively correlated with the average pore diameter, porosity, and specific surface area of Aramid paper-based materials, but negatively correlated with its tensile index, tear index, and compressive strength. Fractal dimension can be available to study the pore structure, and the advantages and disadvantages of the mechanical and insulation properties of Aramid paper-based materials. Liu et al. [37] established the fractal structure of wetting line by using the internal growth mode of half hole circular arc, and included the accumulation effect of inertial force on the circular arc into Bosanquet’s inertial force imbibition mechanism. The fractal dimension and pore size range of paper coating materials were measured by the FHH model of multi-layer adsorption of gas molecules in porous media. The fractal dimension and pore size range are reasonable and normal, and the fluid inertia force has a positive effect on the rapid imbibition in mesoporous and nano channels. Not only the structural parameters of paper coating materials have fractal characteristics, but also the bending properties of capillary tubes in the process of imbibition [38], and the wetting angle of rough surfaces [39]. According to the fractal characteristics of pores in porous media, considering the capillary pressure, gravity, and fracture from spontaneous absorption of wetting liquid into saturated porous media of gas (especially the mechanism of fracture enhanced spontaneous imbibition), a fractal model of fracture index for single-sided fracture is established, which could study the relationship between the cumulative mass and the contact area, pore fractal dimension, curvature, maximum pore size, porosity, liquid density and viscosity, surface tension, contact angle, crack height and inclination angle of wetting liquid [40]. The probability model of the Kozeny-Carman constant of fibrous porous media is erected by the fractal Monte Carlo technique, as seen in Figure 5. The model is a function of structural parameters of fibrous porous media, including porosity, pore size, fiber diameter, curvature, and area fractal dimension, which can represent other transmission features of fluid in fibrous porous media [41]. The improved fractal structure of Sierpiński carpet can reconstruct the porous media model, which is applied to simulate the fluid seepage process under the potential difference through the random walk process of particles with certain directivity in the pore channel. The quantitative characterization of the complex pore structure of porous media is realized by the directional random walk fractal spectrum dimension; the larger the fractal dimension of random walk in the direction, the greater the seepage performance in this direction, namely, the better the connectivity of pore channels; nevertheless, there is a huge gap between the simulation results and the actual three-dimensional flow process of porous media [42].

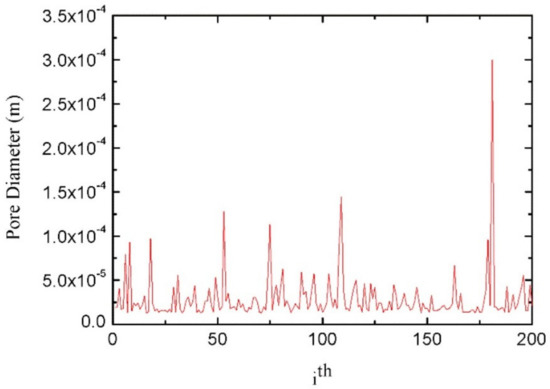
Materials 14 00860 g010 550

Figure 5. The capillary sizes simulated by Xiao’s Fractal-Monte Carlo simulations with poroity of 70%.

The above research on porous materials is based on the classical mechanical theory. The continuity assumption is applicative in many practical applications, such as space, air flow and water flow. Even so, if molecules diffuse in water, the water will become intermittent; in the framework of a continuum hypothesis, the movement of molecules will become completely unpredictable [43]. Fractal dynamics takes place on a very small-time scale, which is a discontinuous system. Fractal calculus [44][45] can be used to describe the molecular motion in this term. Fractal calculus is a comparatively new concept, which is able to productively handle fractal dynamics by replacing continuous time with fractal time [46][47]. Fractal calculus can effectively simulate various phenomena in porous media or hierarchical structure, and reveal the hidden mechanism that cannot be found in continuum mechanics [48][49].

In summary, for many packaging materials’ preparation and performance analysis process, a new processing could be first using SEM, TEM, SAXS, and other imaging technologies to obtain object images, or utilizing mercury intrusion method to extract the fractal features of porous materials, and then employing fractal dimension calculation methods, such as box counting dimension, multifractal method, Hurst index, and signal fractal dimension calculation method, finally, establishing the relationship between fractal dimension and material properties. This method may be a reference for other materials that have not been analyzed by fractal theory, and may become a new and better performance analysis method. With the deepening of fractal dynamics research, the establishment of the relationship between fractal dimension and material properties is expected to provide a new method for predicting material properties on a small scale.

This entry is adapted from the peer-reviewed paper 10.3390/ma14040860

References

  1. Mandelbrot, B.B. Stochastic Models for the Earth’s Relief, the Shape and the Fractal Dimension of the Coastlines, and the Number-area Rule for Islands. Proc. Natl. Acad. Sci. USA 1975, 72, 3825–3828.
  2. Sun, J.; Ji, Z.; Zhang, Y.; Yu, Q.; Ma, C. A Contact Mechanics Model for Rough Surfaces Based on a New Fractal Characterization Method. Int. J. Appl. Mech. 2018, 10, 1850069.
  3. Ma, J.; Liu, D.; Chen, Y. Random Fractal Characters and Length Uncertainty of the Continental Coastline of China. J. Earth Syst. Sci. 2016, 125, 1615–1621.
  4. Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal Analysis of Financial Markets: A Review. Rep. Prog. Phys. 2019, 82.
  5. Dimri, V.P.; Ganguli, S.S. Fractal Theory and Its Implication for Acquisition, Processing and Interpretation (API) of Geophysical Investigation: A Review. J. Geol. Soc. India 2019, 93, 142–152.
  6. Tang, S.W.; He, Q.; Xiao, S.Y.; Huang, X.Q.; Zhou, L. Fractal Plasmonic Metamaterials: Physics and Applications. Nanotechnol. Rev. 2015, 4, 277–288.
  7. Jeldres, R.I.; Fawell, P.D.; Florio, B.J. Population Balance Modelling to Describe the Particle Aggregation Process: A review. Powder Technol. 2018, 326, 190–207.
  8. Dan-Ling, W.D.; Juan-Fang, L.I. A Study on the Characteristics of Liquid-vapor Interface by Using Fractal Theory. In Proceedings of the International Symposium on Heat Transfer & Energy Conservation, Guangzhou, China, 11–15 January 2004.
  9. Zhou, J.; Sancaktar, E. Yield Behavior of Moderately Filled Epoxy/Ni Suspensions. J. Adhes. Sci. Technol. 2010, 24, 1929–1948.
  10. Solov’Yov, I.A.; Solov’Yov, A.V. Simulation of nanofractal dynamics with MBN Explorer. J. Phys. Conf. Ser. 2013, 438, 012006.
  11. Santillán, J.M.J.; Van Raap, M.F.; Zélis, P.M.; Coral, D.F.; Muraca, D.; Schinca, D.C.; Scaffardi, L.B. Ag nanoparticles formed by femtosecond pulse laser ablation in water: Self-assembled fractal structures. J. Nanoparticle Res. 2015, 17, 17.
  12. Xiao-Xu, L.; Jing-Hua, Y.; Dao-Bin, S.; Wen-Bin, B.; Wei-Dong, C.; Zhong-Hua, W. Small-Angle X-Ray Scattering Study on Nanostructures of Polyimide Films. Chin. Phys. Lett. 2010, 27, 27.
  13. Tian, D.; Li, X.; He, J.-H. Self-assembly of macromolecules in a long and narrow tube. Therm. Sci. 2018, 22, 1659–1664.
  14. Pandey, I.; Chandra, A. Factors affecting fractal patterns obtained by electroless deposition in polymer. Mater. Res. Express 2019, 6, 105307.
  15. Ritter, J.E.; Huseinovic, A. Adhesion and Reliability of Epoxy/Glass Interfaces. J. Electron. Packag. 2000, 123, 401–404.
  16. Ji, N.P.; Kaifeng, Z. Fractal Characterization of Uniformity of Discrete Phase in Nanocomposites. J. B. Univ. Aeronaut. Astronaut. 2009, 35, 852–855.
  17. Shaoqun, Z.; Jun, H.; Wei, X.; Guangwei, C.; Yangjun, L.; Wei, S.; Jiaxiong, Y. Fracture Features and the Relationship between Wood Shear Strength and Fractal Dimension. Sci. Silvae Sin. 2015, 51, 127–134.
  18. Wang, C.; Smith, L.M.; Wang, G.; Shi, S.Q.; Cheng, H.; Zhang, S. Characterization of interfacial interactions in bamboo pulp fiber/high-density polyethylene composites treated by nano CaCO3 impregnation modification using fractal theory and dynamic mechanical analysis. Ind. Crop. Prod. 2019, 141, 111712.
  19. Starodubtseva, M.; Starodubtsev, I.E.; Starodubtsev, E.G. Novel fractal characteristic of atomic force microscopy images. Micron 2017, 96, 96–102.
  20. Gabibov, I.A.; Dyshin, O.A.; Rustamova, K.B. Formation of the properties of the structure of disperse-filled polymer composites. Plast. Massy 2019, 23–26.
  21. Xue, M.G.; Wang, S.F. The Analysis of Relationships between Surface Porosity and Air Permeability of Paper (board). Adv. Mater. Res. 2011, 396–398, 1426–1429.
  22. Campano, C.; Balea, A.; Ángeles, B.; Negro, C. A reproducible method to characterize the bulk morphology of cellulose nanocrystals and nanofibers by transmission electron microscopy. Cellulose 2020, 27, 4871–4887.
  23. Ferreira, W.H.; Dahmouche, K.; Andrade, C.T. Dispersion of reduced graphene oxide within thermoplastic starch/poly(lactic acid) blends investigated by small-angle X-ray scattering. Carbohydr. Polym. 2019, 208, 124–132.
  24. Codou, A.; Misra, M.; Andrzejewski, J. Sustainable biocomposites from Nylon 6 and polypropylene blends and biocarbon—Studies on tailored morphologies and complex composite structures. Compos. Part. A Appl. Sci. Manuf. 2020, 129, 105680.
  25. Xian, Y.; Wang, C.; Wang, G.; Smith, L.; Cheng, H. Fractal dimension analysis of interface and impact strength in core–shell structural bamboo plastic composites. Iran. Polym. J. 2017, 26, 169–178.
  26. Wei, F.; Wang, W.; Zhang, J. Fractal Characterization of Section Impact Strength of Polypropylene Compound Packaging Materials. Packag. Eng. 2016, 37, 61–65.
  27. Zhang, C. Tensile Strength and Fractal Characteristics of SiC Filled PP/FA Composites. Packag. Eng. 2017.
  28. Lu, D.R.; He, C.X. Quantitative Analysis of Microcracks in Nano-ALN /PTFE Composites Based on Fractal Theory. In Proceedings of the 10th Sino-Japanese Composite Materials Academic Conference, Chengdu, China, 8 September 2012; pp. 136–139.
  29. Chen, Y.; Deng, Z.; Cheng, Q. Thermal conductivity of Si/Ge nanocomposites with fractal tree-shaped networks by considering the phonon interface scattering. Int. J. Heat Mass Transf. 2015, 88, 572–578.
  30. Minakova, N.N.; Ushakov, V.Y. Application of Texture Analysis to Assess the Operability of Filled Polymers at High Temperatures. Russ. Phys. J. 2016, 58, 1627–1634.
  31. Wu, C.; Liu, C.; Chen, Z.; Liang, J. Fractal Quantitative Characterization of Disperse Effect of Glass Beads in Filled Polypropylene Composites. Eng. Plast. Appl. 2016, 44, 92–97.
  32. Zhu, Q.; Zhang, C.; Yang, W. The Influence of permeability on the ablation process for an ablative material. Fractals 2019, 27, 27.
  33. Jelčič, Ž.; Holjevac-Grguric, T.; Rek, V. Mechanical properties and fractal morphology of high-impact polystyrene/poly(styrene-b-butadiene-b-styrene) blends. Polym. Degrad. Stab. 2005, 90, 295–302.
  34. Devakul, T.; You, Y.; Burnell, F.J.; Sondhi, S. Fractal Symmetric Phases of Matter. SciPost Phys. 2019, 6, 007.
  35. Silva, F.; Gonçalves, L.; Fereira, D.; Rebello, J. Characterization of failure mechanism in composite materials through fractal analysis of acoustic emission signals. Chaos Solitons Fractals 2005, 26, 481–494.
  36. Zhang, M.; Jiang, M.; Lu, Z.; Liu, G.; Song, S.; Yang, B. Characterization of Structure and Properties of Para-Phenylene Terephthalamide Paper-Based Composites by Fractal Dimension. Polym. Mater. Sci. Eng. 2015, 31, 96–101.
  37. Liu, G.; Zhang, M.; Ridgway, C.J.; Gane, P.A.C. Spontaneous Inertial Imbibition in Porous Media Using a Fractal Representation of Pore Wall Rugosity. Transp. Porous Media 2014, 104, 231–251.
  38. Jian-Chao, C.; Yu, B.; Mao-Fei, M.; Liang, L. Capillary Rise in a Single Tortuous Capillary. Chin. Phys. Lett. 2010, 27, 054701.
  39. Onda, T.; Shibuichi, S.; Satoh, A.N.; Tsujii, K. Super-Water-Repellent Fractal Surfaces. Langmuir 1996, 12, 2125–2127.
  40. Cai, J.; Sun, S. Fractal Analysis of Fracture Increasing Spontaneous Imbibition in Porous Media with Gas-Saturated. Int. J. Mod. Phys. C 2013, 24.
  41. Xiao, B.; Zhang, X.; Jiang, G.; Long, G.; Wang, W.; Zhang, Y.; Liu, G. Kozeny–Carman constant for gas flow through fibrous porous media by fractal-monte carlo simulations. Fractals 2019, 27, 1950062.
  42. Li, X. Research on Porous Media Seepage Based on Directional Random Walking Method. Master’s Thesis, Yangzhou University, Yangzhou, China, 2018.
  43. Kosmidis, K.; Macheras, P. On the Dilemma of Fractal or Fractional Kinetics in Drug Release Studies: A Comparison Between Weibull and Mittag-Leffler Functions. Int. J. Pharm. 2018, 543, 269–273.
  44. Su, W. Construction of Fractal Calculus. Sci. Sin. Math. 2015, 45, 1587–1598.
  45. Aln, Q.T.; He, J.H. On Two-Scale Dimension and Its Applications. Therm Sci. 2019, 23, 1707–1712.
  46. Coronel-Escamilla, A.; Gomez-Aguilar, J.F.; Torres, L.; Escobar-Jimenez, R.F. A Numerical Solution for a Variable-Order Reaction-Diffusion Model by Using Fractional Derivatives with Non-Local and Non-Singular Kernel. Phys. A 2018, 491, 406–424.
  47. Gomez-Aguilar, J.F. Chaos in a nonlinear Bloch System with Atangana-Baleanu Fractional Derivatives. Numer Meth. Part. D E 2018, 34, 1716–1738.
  48. Coronel-Escamilla, A.; Gomez-Aguilar, J.F.; Baleanu, D.; Cordova-Fraga, T.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H.; Al Qurashi, M.M. Bateman-Feshbach Tikochinsky and Caldirola-Kanai Oscillators with New Fractional Differentiation. Entropy 2017, 19, 55.
  49. Aguilar, J.F.G.; Cordova-Fraga, T.; Torres-Jimenez, J.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H.; Guerrero-Ramirez, G.V. Nonlocal Transport Processes and the Fractional Cattaneo-Vernotte Equation. Math. Probl. Eng. 2016, 2016.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback