A watershed is defined by natural topographic boundaries as an ecosystem of integrated terrestrial and aquatic systems, rather than the political boundaries, in which all of the incoming precipitation and snowmelt are collected into the stream reaches while a river basin is an area of land drained by a river, its tributaries and watersheds.
- watershed modeling
- cold climate
- climate change
- modeling of river basins
1. Introduction
A watershed is defined by natural topographic boundaries as an ecosystem of integrated terrestrial and aquatic systems, rather than the political boundaries, in which all of the incoming precipitation and snowmelt are collected into the stream reaches while a river basin is an area of land drained by a river, its tributaries and watersheds. The watershed function is generally defined as its response to the water entering its control volume [1][2]. The river shape, land topology, wetlands and riparian zones regulate the overland and subsurface flows as well as groundwater. Water budget in a watershed is balanced by precipitation, evapotranspiration, infiltration, and runoff. For a cold region, glacier, snowpack, permafrost, etc. (frozen water components) are also important parts of water budget. Some of the models discussed in this paper may not have a good process to capture those budgets. Watershed ecosystems are controlled by a suite of hierarchically nested physical, chemical, and biological processes operating over space and time.
A watershed consists of terrestrial or aquatic sub-ecosystems, including forest, grasslands, arable, urban, and wetlands. Water, energy, air, vegetation and land interact within the watershed. Some main watershed processes can be broken down into specific functions and characteristics, including hydrological processes (i.e., overland flow, evaporation, infiltration, groundwater recharge, and erosion), biogeochemical processes (i.e., nutrient cycling, pollution transport and fate, mineralization and organic matter decomposition), and land-surface interaction (i.e., plant growth, photosynthesis, and evapotranspiration). In cold regions, there are four special elements, including snow, permafrost, freeze-thaw cycle and glaciers as well as lake and river ices (Figure 1) [3]. The biogeochemical processes, such as nitrification, denitrification and decomposition, can be affected by soil water, temperature and pH, depending on various hydrological processes. Human activities, such as land use changes, mining and water policy can also affect water balance and biogeochemical processes. Intensive agricultural practices, such as grazing, irrigation and fertilization, can affect hydrological and biogeochemical processes, and cause land degradation, such as salinization and desertification [4].
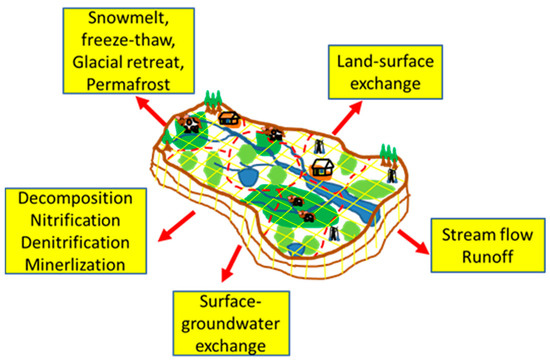
Figure 1. Watershed ecosystem processes at larger spatial scales (heavy arrows).
2. Principles of Watershed Modelling
Watershed modeling is to quantify hydrology and biogeochemistry with associated ecosystem functions, such as plant dynamics, in the watershed. An ideal basin-oriented strategy is to simulate the integration of watershed hydrology, nutrient, and sediment reactive transport below and above ground [5]. However, in reality, we cannot include all detailed watershed processes. Hence, abstraction through parameterization and simplification is necessary in representing complexity level of watershed system and processes. The parameterization and simplification are a compromise between reality, feasibility, and simplicity in a watershed model and are to use some replacement of watershed processes using a model of similar but simpler, more empirical conceptual structure. The point is not a perfect solution but a replacement to reflect the physical reality as good as possible. Thus, a watershed model is an approximation of its reality to describe the watershed processes and system which can retain most of its important characteristics [6][7].
Conceptually, it is quite natural to use a symbolic watershed model to represent some of the natural hydrological and biogeochemical processes of the real system according to the first principle. A set of equations of mass, momentum, and energy conservation along with initial and boundary conditions can be established to describe the streamflow, infiltration, subsurface flow, and baseflow in a watershed system driven by the weather conditions, such as precipitation and solar radiation, soil and plants. Unfortunately, these equations cannot be solved analytically and can be solved only for very simple geometries or boundary conditions. Therefore, a watershed domain is usually distributed on discrete grids and the partial differential equations are replaced by their discrete equations. For example, the Richards equation of water transport in soil are solved by using finite difference method [8][9][10][11][12]. However, such models require extensive data and physical parameter, which may not be efficient to set up the model. Furthermore, a watershed model needs to consider readily available data with sufficient efficiency of computer power and memory while simulating large river basins. This will allow realistic simulation of some medium complexity, which generally includes relatively detailed data inputs such as topography, land use, soil, weather, and water quality. Thus, many distributed models delineate a watershed into a multi-level hierarchically distributed drainage system using reasonable spatial discrete elements, such as sub-basins and hydrological response units (HRUs) in SWAT [13], CRHM [14] and HSPF [15], and a grid of large (>>1 km), flat, uniform cells in the VIC (Table 1). These watershed models not only represent the fundamental water and sediment transport processes, but also combine the empirical and statistical equations such as nitrification, denitrification and decomposition. The use of the lumped parameters and HRUs or similar units are to reduce the grid number because the computational cost depends on the numbers of grid cells and parameters [16].
Table 1. Characteristics of watershed models in cold regions.
| Model Name | Spatial Resolution | Time Step | Snowpack Model | Snowpack Layer | Water Quality | GHGs | References |
|---|---|---|---|---|---|---|---|
| HSPF | HRUs | Sub-daily | Snowmelt/sublimation/ compaction/albedo/blowing/radiation/interception | Two layers | Yes | ||
| CRHM | HRUs | Daily | Snowmelt/sublimation/ compaction/albedo/blowing/radiation/interception | Two layers | [14] | ||
| CRHM+ WINTRA | HRUs | Daily | Snowmelt/sublimation/ compaction/albedo/blowing/radiation/interception | Two layers | Yes | ||
| SWAT | HRUs | Daily | Snowmelt/sublimation | One layer | Yes | ||
| VIC | Grid cell (>>1 km2) |
Daily | Snowmelt/sublimation/ compaction/albedo/blowing/radiation/interception | Two layers | Yes | ||
| SWAT-DayCent | HRUs | Daily | Snowmelt/sublimation | One layer | Yes | N2O/CO2 | |
| SWAT-MKT | HRUs | Daily | Snowmelt/sublimation | One layer | Yes | N2O/CO2/NEE | |
| VIC-CropSyst | Grid cell (>>1 km2) |
Daily | Snowmelt/sublimation/ compaction/albedo/blowing/radiation/interception | Two layers | Yes |
In every HRU unit, the parameters of a watershed model represent a volume-average of their variability over the unit that consists of homogeneous land use, management and soil properties, slopes and weather conditions. In the HRUs, only percentages of the land uses are represented, and parameters, such as soil properties and land uses are not identified spatially in these models. For example, in the VIC model, the sub-grid variability is handled in terms of statistical properties. Therefore, land-atmosphere fluxes, and the water and energy balances are calculated at a daily or sub-daily time step but horizontal flow between HRUs is not considered. The water balance is calculated among rainfall, runoff, infiltration, evapotranspiration, storage, snowmelt water, lateral subsurface flow from the soil layers and baseflow at each HRU. Flows are aggregated from all HRUs to the sub-basin level, and then directed to stream reaches along the directions of element slopes using either the variable-rate storage method or the Muskingum method. Sediment, nutrient, pollutants, and bacteria loading from each HRU are also collected at the subbasin outlets, and are directed to channels, ponds, wetlands, and lakes. Contributions from point sources and urban areas can be inputted from HRUs and be exported from each sub-basin.
This entry is adapted from the peer-reviewed paper 10.3390/w13040518
References
- Chen, X.; Lee, R.M.; Dwivedi, D.; Son, K.; Fang, Y.; Zhang, X.; Graham, E.; Stegen, J.; Fisher, J.B.; Moulton, D.; et al. Integrating field observations and process-based modeling to predict watershed water quality under environmental perturbations. J. Hydrol. 2020, 125762, 125762.
- Wagener, T.; Sivapalan, M.; Troch, P.; Woods, R. Catchment classification and hydrologic similarity. Geogr. Compass 2007, 1, 901–931.
- Hock, R.; Rasul, G.; Adler, C.; Cáceres, B.; Gruber, S.; Hirabayashi, Y.; Jackson, M.; Kääb, A.; Kang, S.; Kutuzov, S.; et al. High mountain areas. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate. Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; IPCC: Geneva, Switzerland, 2019; in press.
- Wang, J.; Li, Y.; Bork, E.W.; Richter, G.M.; Eum, H.-I.; Chen, C.; Shah, S.H.H.; Mezbahuddin, S. Modelling spatio-temporal patterns of soil carbon and greenhouse gas emissions in grazing lands: Current status and prospects. Sci. Total. Environ. 2020, 739, 139092.
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290.
- Singh, V.P.; Woolhiser, D.A. Mathematical modeling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292.
- Woolhiser, D.A. Hydrologic and Watershed Modeling-State of the Art. Trans. ASAE 1973, 16, 553–559.
- Yeh, G.-T.; Shih, D.-S.; Cheng, J.-R.C. An integrated media, integrated processes watershed model. Comput. Fluids 2011, 45, 2–13.
- Ma, L.; He, C.; Bian, H.; Sheng, L. MIKE SHE modeling of ecohydrological processes: Merits, applications, and challenges. Ecol. Eng. 2016, 96, 137–149.
- Deng, B.; Wang, J. Saturated-unsaturated groundwater modeling using 3D Richards equation with a coordinate transform of nonorthogonal grids. Appl. Math. Model. 2017, 50, 39–52.
- Langevin, C.D.; Hughes, J.D.; Banta, E.R.; Niswonger, R.G.; Sorab, P.; Provost, A.M. Documentation for the MODFLOW 6 Groundwater Flow Model. In U.S. Geological Survey Techniques and Methods; Book 6; U.S. Geological Survey: Reston, VA, USA, 2017.
- Orgogozo, L.; Renon, N.; Soulaine, C.; Hénon, F.; Tomer, S.; Labat, D.; Pokrovsky, O.; Sekhar, M.; Ababou, R.; Quintard, M. An open source massively parallel solver for Richards equation: Mechanistic modelling of water fluxes at the watershed scale. Comput. Phys. Commun. 2014, 185, 3358–3371.
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250.
- Pomeroy, J.W.; Gray, D.M.; Brown, T.; Hedstrom, N.R.; Quinton, W.L.; Granger, R.J.; Carey, S.K. The cold regions hydrological model: A platform for basing process representation and model structure on physical evidence. Hydrol. Process. 2007, 21, 2650–2667.
- Skahill, B.E. Use of the Hydrological Simulation Program—FORTRAN (HSPF) Model for Watershed Studies; ERDC/TN SMART-04-1; Army Engineer Research and Development Center: Vicksburg, MS, USA, 2004.
- Wang, J.; Zhang, X.; Bengough, A.G.; Crawford, J.W. Domain-decomposition method for parallel lattice Boltzmann simulation of incompressible flow in porous media. Phys. Rev. E 2005, 72, 016706.
