Introduction^[1]

Since the introduction of the CCR model by professors Abraham Charnes, William Cooper and Edwardo Rhodes in 1978^[2], the way scholars investigate the efficiency and productivity of organizations shifted drastically. The so-called Data Envelopment Analysis (DEA) was different from statistical procedures comparing measures of performance based on an average observation.  Based on Farrell's seminal work ^[3] on the measurement of productive efficiency, the problem of measuring the technical efficiency of Decision Making Units (DMUs) became a matter of how far production is expanded without using additional resources. Measuring the technical efficiency is made by comparing the DMU performance with a hypothetical unit constructed as a weighted average of other observed firms. The interpretation behind Farrell concepts is that if a decision unit can transform input resources into output production in a Pareto-efficient way (i.e. in such a way that there is no other configuration with more production at the same level of resources, or fewer resources resulting in the same level of production) then another unit with similar scale must be capable of producing similar results.

Data Envelopment Analysis is a very dynamic field, which importance has increased more and more over the past decades. Back in the 80s, the first decade of the DEA expansion was timid, restricted to basically two options: the constant ^[2] and (later) variable return to scale ^[4] models. Today, thousands of important models and empirical applications can be traced over several repositories. Daraio et al. (2020) ^[5] offer an interesting review on the many surveys of DEA empirical applications based on the UN standard classification for all the economic activities combined with the economic literature relevant concepts. According to the authors, the topics Banking, Investment, Financial Institutions, Health, Transportation and Agriculture are some of the fields having the greatest coverage by surveys of empirical assessments. In addition, computational developments are in continuous expansion. In addition, Daraio et al (2019) ^[6] investigate the 53 most used packages, software, solvers, web programs, libraries and language-based routines used to perform frontier models (DEA and SFA – Stochastic Frontier Analysis) of the productivity and efficiency analysis. This systematic survey highlights an increasing availability of open-source toolboxes and software for the implementation of many alternative DEA models. Other motivating and recent bibliometric reviews in the field can be found in Cook & Seiford (2009) ^[7],Lampe & Hilgers (2015) ^[8], Zhou & Xu (2020) ^[9] and Peykani et al. (2020) ^[10].

Methodology^[1][7][11]

The Data Envelopment Analysis (DEA) methodology introduced by Abraham Charnes and colleagues estimates an efficiency frontier by considering the best performance observations (extreme points) which “envelop” the remaining observations using mathematical programming techniques. The concept of efficiency can be defined as a ratio of produced outputs to the used inputs:

   (1)

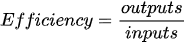
So that an inefficient unit can become efficient by expanding products (output) keeping the same level of used resources, or by reducing the used resources keep the same production level, or by a combination of both ^[11][12][13]

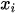
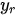
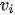
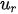
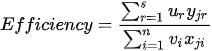
Considering j = 1, 2, 3, . m Decision Making Units (DMUs) using | i = 1, 2, 3, ., n inputs to produce | r = 1, 2, 3, ., outputs and prices (multipliers) and  associated with those inputs and outputs, we can also formalize the efficiency expression in (1) as the ratio of weighted outputs to weighted inputs:

     (2)

In Charnes et al. (1978) ^[2] DEA methodology the multipliers, and a measure for the technical efficiency for a specific DMU can be estimated by solving the fractional programming problem ^[7]:

     (3)

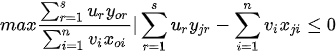
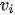
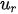
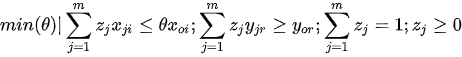
For all j, r and i, and strict positive and  . This problem is denominated the CCR constant return to scale input-oriented model, which by duality is equivalent to solving the following linear programming ^[7]:

     (4)

As a result, we have an efficiency score θ which varies from 0 to 1 designating the efficiency for each decision making unit. We can obtain the marginal contribution of each input and output in the multiplier model of (3), the peers of efficiency and respective weights in the primal (or envelopment) form of (4), and also the potential for improvements and slacks in an extension form of (4).

This entry refers to 10.1504/ijor.2020.10035180.