Outlier Detection | Encyclopedia MDPI

Outlier Detection: History

Please note this is an old version of this entry, which may differ significantly from the current revision.

Subjects: Others

Contributor:

Outlier detection is a statistical procedure that aims to find suspicious events or items that are different from the normal form of a dataset.

Outlier Detection
Anomaly Detection
Local Outlier Detection
Stream Data Mining
Data Cleaning

1. Introduction

Outlier detection is the term used for anomaly detection, fraud detection, and novelty detection. The purpose of outlier detection is to detect rare events or unusual activities that differ from the majority of data points in a dataset [1]. Recently, outlier detection has become an important problem in many applications such as in health care, fraud transaction detection for credit cards, and intrusion detection in computer networks. Therefore, many algorithms have been proposed and developed to detect outliers. However, most of these algorithms are designed for a static data environment and are difficult to apply to streams of data, which represent a significant number of important application areas.

Outlier detection can be viewed as a specific application of generalized data mining. The process of data mining involves two steps: data processing and data mining. The aim of data processing is to create data in good form, i.e., the outliers are removed. Data mining is the next step, which involves the discovery and understanding of the behavior of the data and extracting this information by machine learning [2]. Outlier detection (or data cleaning) is an important step in data processing because, if an outlier data point is used during data mining, it is likely to lead to inaccurate outputs [3]. For example, a traffic pattern of outliers in the network might mean the data has been sent out by a hacked computer to an unauthorized device [4]; if the outliers cannot be detected and removed, a machine learning technique applied to the data is likely to be misled. Additionally, in many cases, the goal of data mining is to find the outliers. For example, an outlier image in magnetic resonance imaging could mean the presence of malignant tumors [5]. An outlier reading from an aircraft sensor may indicate a fault in some components of the aircraft [6].

Outlier detection (also known as anomaly detection) is split into two types, global and local detection. For a global outlier, outlier detection considers all data points, and the data point pt is considered an outlier if it is far away from all other data points [7]. The local outlier detection covers a small subset of data points at a time (Figure 1). A local outlier is based on the probability of data point pt being an outlier as compared to its local neighborhood, which is measured by the k-Nearest Neighbors (kNN) algorithm [8].

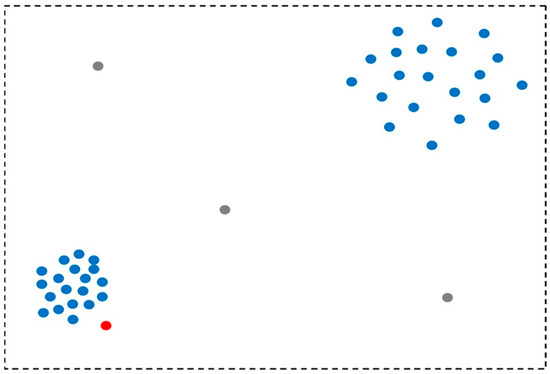
Figure 1. The types of outliers, where grey points are global outliers, and the red point is a local outlier.

Recently, many studies have been published in the area of outlier detection, and there is a need for these studies to be reviewed to understand the depth of the field and the most promising areas for additional research. This review is focused on local outlier detection algorithms in data stream environments. This review is distinguished from previous reviews as it specifically covers the Local Outlier Factor (LOF) algorithms in data stream environments and reviews the most recent, state-of-the-art techniques. In this paper, different methods and algorithms for local outlier detection are summarized. The limitations and challenges of the LOF and other local outlier detection algorithms in a stream environment are analyzed. Moreover, new methods for the detection of an LOF score in a data stream are proposed. This literature review will greatly benefit researchers in the field of local outlier detection because it provides a comprehensive explanation of the features of each algorithm and shows their strengths and weaknesses, particularly in a data stream environment. The paper has five remaining parts: the second section is Related Works and Background; the third section is Literature Review Methodology; the fourth section is Literature Review Results; the fifth section is Analysis and Discussion; and the sixth section is the Conclusion.

2. Literature Review Methodology

The aim of this literature review is to report on current works using the LOF with a focus on local outlier detection in data streams. It also proposes a new methodology for a more efficient LOF in data streams. This paper focuses on the research that was conducted from May 2000 to April 2020. The search took place through research papers in electronic databases published in English. These databases were Google Scholar, IEEE Xplore, ACM, Springer, Science Direct, and MDPI. Keywords including outlier detection, local outlier detection, local outlier detection in data streams, Local Outlier Factor in data streams, and data stream mining were used. In the initial search, a total of 528 papers were reviewed by title and abstract. The selected papers were then categorized into two sections: the static environment and the stream environment. After that, the selected papers were filtered by the full text. The total number of selected papers was 47 (Figure 2). In the static environment subsection, the local outlier detection papers with the most citations were selected to be reviewed in greater detail, while the remaining papers were reviewed more briefly. In the stream environment subsection, the recent state-of-the-art papers on the LOF in data streams were reviewed in detail, while the remaining papers were reviewed briefly.

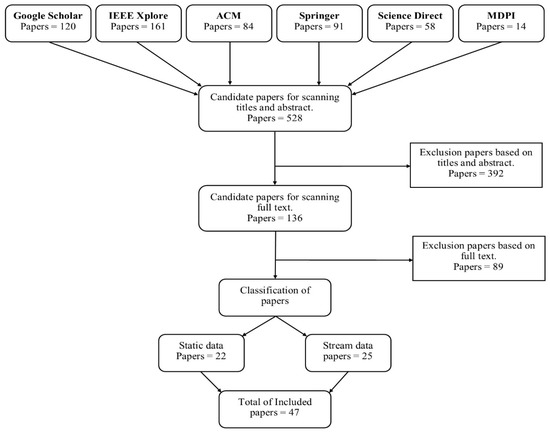
Figure 2. The search strategy flowchart for selecting articles.

The criteria for inclusion in this literature review were the following: (1) the article contained a new density—based local outlier detection algorithm in a static environment, (2) the local outlier detection algorithm was an unsupervised algorithm, (3) the article contained a new LOF algorithm for a stream environment, or (4) it included a local outlier detection algorithm in a stream environment. The research questions that have been answered in this literature review are the following: (1) what are the LOF algorithm problems and challenges in stream environments, (2) what are the existing methods and techniques that have been applied to the LOF in a stream environment, (3) what are the existing local outlier detection algorithms that need to be developed in order to work in a stream environment, and (4) how does the new methodology execute the LOF efficiently in a stream environment?

3. Analysis and Discussion

We are now in the era of big data that is mined and analyzed to extract information. Data science, statistics, and machine learning are the fields where researchers are most interested in methods of extracting information from big data. Outlier detection is a major operation in these fields. Outlier detection is a task in data mining that has gained a lot of attention in this era of big data and an important type of big data is data streams. With the growing necessity of mining and analyzing data streams, it has become hard to use traditional outlier detection algorithms efficiently [108]. The LOF is an efficient and powerful algorithm for detecting local outliers. The main problem of the LOF is that it requires storage in computer memory of the whole dataset and the distance values [109]. A different issue with the LOF is that it requires recalculation from the beginning if any modification occurs in the dataset, such as the insertion of a new data point. The ILOF is a modified version of the LOF that can work in stream environments. Nevertheless, the ILOF also needs to keep all the data points in the computer memory in order to calculate the LOF score for every data point insertion that arrives at different times. Therefore, ILOF requires a large use of memory and computational time.

3.1. Computational Complexity

The LOF and the related local outlier detection algorithms are nearest neighbor-based algorithms. The computational complexity of these algorithms is O(n²), except for LOCI. Therefore, the execution times of these algorithms are similar. The computational complexity of the LOCI algorithm is O(n³), which requires more execution time because of the repetition required for the radius expansion. Another version of the LOCI algorithm is the aLOCI, which is faster than the LOCI because the execution time is based on the number of quad trees. The nearest neighbor-based algorithms have better accuracy of outlier detection than cluster-based algorithms [110]. However, long computation times are the cost of these methods because of the long time spent calculating pairwise distances.

When comparing the cluster-based algorithms with nearest neighbor-based algorithms, the cluster-based algorithms are more efficient; for example, the k-means computational complexity is O(nki), where n is the data point, k is the center of the cluster, and i is repetitions. By contrast, the nearest neighbor-base algorithms usually lead to quadratic computational complexity because they calculate the distances of all data points. The computational complexity of cluster-based algorithms, such as CBLOF, depends on the cluster algorithm, which is faster than O(n²) when using k-means. Therefore, the clustering algorithm is the essential reason for the computational complexity.

The most important issue for the LOF and its extensions is application in a stream environment. Few works exist in this domain, but some of them show better execution times. The ILOF algorithm addresses the issue of the LOF in a stream environment by updating and calculating the score of the LOF when a new data point arrives by using a landmark window. The computational complexity of the ILOF is O(N log N) and the memory usage complexity is O(Nk). The MILOF algorithm solved the issue of unlimited memory in the ILOF by summarizing the data points using k-means clustering and sliding windows, which limits the memory requirement. The computational complexity of the MILOF is O(N log Ws) and the memory usage complexity is O(Ws k), where N is the size of the data stream and Ws is the window size. The DILOF algorithm overcomes the issue of unbounded memory requirements by summarizing the data points using gradient-descent and sliding windows. The computational complexity of the DILOF is O(N Ws) and the memory usage complexity is O(Ws k). Finally, the MILOF and the DILOF solve the issue of the ILOF by summarizing and keeping only a small portion of the data points, which leads to reduced execution time.

3.2. Strengths and Weaknesses of Existing Methods

3.2.1. Nearest Neighbor-Based Techniques

Distance and similarity metrics can be determined by different approaches in the nearest neighbor-based outlier detection methods. The advantage of this approach is that it does not need an assumption for the data distribution and can be applied to different data types. However, it requires an appropriate distance calculation for the data. The Euclidean distance is the optimal approach for serving the outlier detection in continuous characteristics such as data streams [111]. The methods depend on two approaches:

The use of techniques to measure the distance of the data point as for the outlier score.
To identify the outlier score, the calculation of the relative density of each data point.

However, nearest neighbor-based techniques require a long computational time for big data.

3.2.2. Clustering-Based Techniques

In data mining, the clustering technique is a common alternative for clustering data with similar features [112,113]. Clustering is also an effective method for the study of outliers. In most of the clustering approaches, the primary assumption is that the normal data is often bound to density and significant clusters, where outliers can be separated into other classes [114]. The advantages of cluster approaches include the following:

With the incremental model, it is simple to adjust.
No oversight is required.
Suitable for temporal data to detect outliers.
Requires only a quick test step since the number of clusters needing comparison is typically small.

The disadvantages in the clustering-based techniques are the following:

They depend strongly on the efficiency of the clustering algorithm for normal data points.
The majority of approaches that identify outliers are cluster by-products and thus are not designed to perform well for detecting outliers.
Several cluster approaches process each point to be distributed in some clusters. This could contribute to abnormalities in a large cluster, and techniques that work under the presumption that anomalies are included in each cluster may be viewed as normal data points.
Some algorithms demand that each data point is allocated on a cluster. A wide cluster may be used for outliers and handled by methods that often conclude that outliers are isolated.
Various approaches to the cluster are only applicable where outliers are not part of the main clusters.
The measurement of the clustering algorithm is complicated.

3.3. New Methods to Be Explored

To address the limitation of the LOF in data streams, new methods should be developed. The primary purpose of any new method would be to measure the LOF score in all of the following circumstances: (1) keeping only a small part of the dataset in the computer memory; (2) the algorithm has no prior knowledge about the data distribution; (3) for an incoming data point pt, the algorithm should verify whether it is an outlier or inlier at the current time T; and (4) when the algorithm detects the current outlier, it has no prior knowledge about future data points.

To overcome the problems of the LOF in stream environments, we have designed a new methodology to detect local outliers. This methodology contains two phases: (1) the detection phase and (2) the summarization phase. For the detection phase, the ILOF is used with a skipping scheme [75,77]. For the summarization phase, the Genetic Density Summarization algorithm (GDS), based on the genetic algorithm (GA), is used to summarize the dataset. The framework of our methodology, named Genetic-based Incremental Local Outlier Factor (GILOF) [115], works as follows: First, the maximum size of the window (W) is determined as W-size. After that, the threshold of the LOF is applied to detect the local outliers, relying on the threshold θ, then using the GDS to summarize the data points. Thereafter, the GILOF uses the ILOF together with a skipping scheme to detect the local outlier when an incoming data point arrives. It is worth noting that the skipping scheme is used in order to detect the sequence of outliers, when the sequence of outliers is outlier data points that are trying to build a new class. The GILOF continues to detect the outlier data points and to compute the LOF values for every new data point until the window reaches the W-size. When the window becomes full, the GDS algorithm is applied to the window in order to summarize 50%W of the older data points in the window; it does so by choosing 25%W of the fittest data points to represent the 50%W of the older data points. After this, the GILOF deletes the older 50%W of the data points from the window and the selected 25%W of data points is transferred to the window and merges with the remaining 50%W. These 75%W of data points joins with the newly incoming data points in the window. When the window reaches the W-size again, the GDS repeats the same process. The video in [116] displays a simulation of the GILOF system process. Figure 7 shows the overall design and workflow for the methodology.

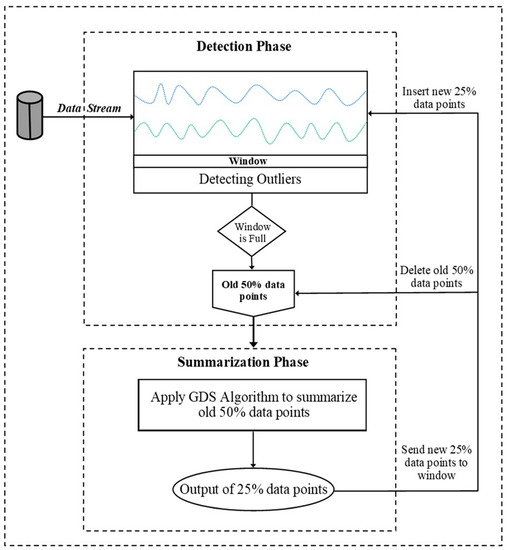
Figure 7. Diagram of the overall design and workflow for the methodology.

Local Outlier Factor by Reachability Distance (LOFR) is similar to the LOF, but the LOFR has a different calculation method, in which it does not need to apply the local reachability density [117]. To calculate the score of outlierness, the LOFR uses k-distance, k-nearest neighbor, and Reachability distance Rd. Subsequently, the Reachability distance Rd of data point p will be divided by the average Rd of the data point p neighbors. This new calculation method for local outlier detection can produce a lower “outlierness” score than the LOF. The LOFR can produce a more accurate outlierness score in various datasets. The LOFR score is calculated by using Equation (6).

(6)

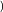
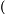
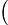
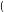
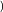
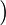
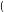
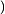
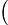
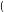
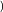
The GILOF algorithm is discussed extensively in [115]. By trying to enhance the effectiveness of the GILOF algorithm, we propose another calculation method for the LOF, which is named LOFR. The newly adapted algorithm in the data stream is named Genetic-based Incremental Local Outlier Factor by Reachability Distance (GILOFR). The GILOFR algorithm is also extensively discussed in [117]. For future work, the other traditional local outlier detection algorithms, such as the COF, LoOP, LOCI, and the INFLO, etc., can be adapted to work in a data stream. To execute these traditional algorithms in a data stream, the mechanisms of the above-mentioned methods, such as the GILOF and DILOF algorithms, should be applied.

This entry is adapted from the peer-reviewed paper 10.3390/bdcc5010001

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.