The water allocation problem is complex and requires a combination of regulations, policies, and mechanisms to support water management to minimize the risk of shortage among competing users. This paper compiles the application of multi-criteria decision-making (MCDM) related to water allocation. In this regard, this paper aims to identify and to discern the pattern, distribution of study regions, water problem classifications, and decision techniques application for a specific water allocation problem. We applied a systematic literature review study from 2000 to 2019 by using four literature databases (Web of Science, Scopus, Science Direct, and Google Scholar). From 109 papers, 49 publications have been identified and information extracted. This study reveals that in the past two decades the application of MCDM in the area of water allocation has increased particularly after 2014. Around 65% and 12% of study papers were conducted in Asia and Europe, respectively. Water shortage, water use management, and water quality were consecutively the most top-ranked discussed water problems. NSGA II (non-dominated sorting genetic algorithm), GA (genetic algorithm), and LP (linear programming) are the more often applied decision methods to solve water allocation problems. The key findings of this study provide guidelines for future research studies.
- database
- MCDM methods
- systematic review
- water allocation
1. Introduction
Water is an essential resource for the existence of every form of life. It is valuable for maintaining a healthy ecosystem and supporting socio-economic development. The availability of water resources varies in physical state, space, and time. Nearly 75% of the earth’s surface is covered by water. However, 97% of the earth’s water is found in oceans and seas and is saline. The remaining 3% of the water on earth is freshwater. A large portion (±68.7%) of freshwater is inaccessible to human beings since it is locked up in glaciers, ice caps, and a permanent snow cover in the polar regions. 30.1% is concentrated as groundwater and 0.9% is surface water (2% rivers, 11% swamps, and 87% lakes) [1,2]. Overall, more than 99% of water is unfit and unavailable for human consumption and only 0.0067% of the total water on earth is fresh and accessible for human water use. The rest requires intensive investment to refine for consumption [1]. This shows freshwater is very important and different water uses should be considered very carefully. At a global level, according to the Cassardo and Jones [1]; FAO [3] report, approximately 70% of water is used for agriculture, mainly in the form of irrigation, 22% for industrial purposes, and 8% for domestic purposes and one percent for recreational use.
Water allocation represents the process of distributing water supplies to fulfill the various requirements of water users. The four questions are: who uses water resources, how, when, and where. Moreover, it determines the allocation of water resources to different purposes in space and time. Water allocation influences the economic, ecological, and socio-cultural aspects of an ecosystem. Water allocation is employed to address various water problems. It is applied in a region (areas) where there are competing demands for water by different users. The demand for water use is determined by quantifying the combining sum of the amount of water required with the amount of water available. To avail water resources continuously in space and time, water infrastructures have been built to store water in various parts of the world. These water storage reservoirs are built either for single or multi-purpose use, for example, for water supply, irrigation, and hydropower production.
At this moment, there is a growing competition for water among different stakeholders. In the past decades, global water demand has increased at a rate of about 1% per year as a function of population growth, economic development, and changing consumption patterns [4]. Further, FAO [3] reported that over the last century, global water withdrawal grew 1.7 times faster than the world population.
Hence, this indicates that the demand for water increases the inter-sectoral competition within the nexus of water, food, and energy. In addition, this drives the concern of sustainable water use. Several studies were conducted to address the multifunctional conflicts with regard to the limited water supply. Some studies established and applied water allocation methods to optimally use water resources in a sustainable manner by considering various socio-economic and environmental factors. Multi-criteria decision-making (MCDM) is the most suitable method adopted to solve multi-objective (criteria) water allocation problems. Different computational multi-criteria decision tools have been designed to support decision-makers. It is substantially important to assess the state of the art regarding MCDM for better understanding and application for future research studies.
2. Classification of MCDM Methods
MCDM is one of the most widely used decision methods to perform mathematical optimization in different fields of applications such as water allocation, land allocation, forest management, energy production, project management and environmental protection, and so on [8,9,10,11]. The application of MCDM has been an active operational research area for many decades [12]. It is an effective tool used to solve complex and conflicting decision problems. It allows the use of both quantitative and qualitative evaluation factors. MCDM is a generic term used for all methods that are useful to solve complex problems. MCDM methods can be classified into two broad classes MADM (multi-attribute decision-making) and MODM (multiple-objective decision-making) [13,14]. MADM is suitable for selection of a limited number of alternatives and preference ranking. The evaluation is based on predetermined decision alternatives with respect to weighted attributes (i.e., the decision space is discrete). Alternatives are the different choices or preferences available for the decision-maker. These alternatives are assumed to be limited in number or finite. They are supposed to be screened, prioritized, and finally ranked or sorted with respect to the stated criteria decisions or objectives.
There are different types of MADM methods (or discrete MCDM) available such as Value/Utility function (e.g., multi-attribute value theory MAVT, multi-attribute utility theory (MAUT), simple additive weighting SAW) [15,16], pairwise comparison (e.g., analytic hierarchy process (AHP),analytic network process ANP) [17,18], distance-based (e.g., technique for order of preference by similarity to ideal solution (TOPSIS)) [19], outranking (e.g., preference ranking organization method for enrichment evaluation (PROMETHEE),and elimination and choice expressing reality (ELECTREE)) [20,21,22]. The MODM method is preferably used for continuous optimization problems where the number of alternatives is infinite, i.e., the decision space is continuous [23]. In general, it is suitable for the design of the best alternative planning decision problems in which alternatives are not predetermined but instead, a set of objective functions is optimized subject to a set of constraints. The MODM methods are further grouped into mathematical programming models and heuristic algorithms based on computational time and solution. For example, mathematical methods include linear programming (LP), non-linear programming, mixed integer linear programming NLP, MILP, goal programming (GP), compromise programming CP, and dynamic programming [24]. Heuristic methods include ones such as simulating annealing (SA), genetic algorithm (GA), non-dominated sorting genetic algorithm (NSGA), and tabu search TS [25,26,27] (Figure 1).
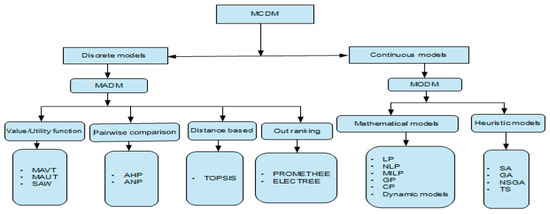
Figure 1. Classification of multi-criteria decision-making (MCDM) methods.
3. Results
3.1. Description of Water Problems and MCDM Methods Application to Solve Water Resource Allocation Problems
3.1.1. MCDM Methods Application to Solve Water Shortage Problems
Water shortage happens when the demand for water use exceeds the supply of water resources in a certain geographical location over a certain time span. The concepts of shortage or scarcity are relative terms. There are quite a number of definitions of water scarcity or shortage. However, there are a few that stand out as robust and well-constructed. In this part, it is not our intention to review all those definitions but to provide an overview of the meaning of what it does refer to. According to FAO [62], it is a concept of describing the relation between demand for water and its availability. It is obvious also that demand and availability are comparative. It varies from place to place, seasons, and local climatic conditions. Water shortage or scarcity is classified into two broad categories i.e., physical scarcity and economic scarcity. Physical scarcity refers to scarcity in availability due to a physical shortage of water resources in a given region. Economic scarcity describes water access due to a lack of adequate infrastructure and institutions to ensure regular water supply [63]. There have been many strategies developed in order to compact water shortage by constructing water resources development structures in different parts of the world. Many researchers have used MCDM in water allocation problems to address the water shortage. Water shortage is the major water allocation problem. Water scarcity is the world’s most challenging problem, Mekonnen and Hoekstra [63] stated about 4 billion people, nearly two-thirds of the world population, experience severe water scarcity at least one month per year. Which is about 66 percent of the world’s population. Almost half of those people reside in India and China. This could increase to some 4.8–5.7 billion in 2050 [48]. The water shortage problem will continue to be a great challenge in the future. Therefore, to address complex multi-objective water shortage problems, it is recommended to use and apply decision-making methods.
In this section, 16 publications used MODM methods, 2 papers applied MADM, and one paper employed both methods to solve water shortage problems. From the heuristic decision methods, NSGA II and GA were predominantly used by 7 publications. The NSGA II decision method was the most frequently used method. The NSGA II method was applied by Uen et al. [64] on the pivotal Shihmen Reservoir, Taiwan, to address the water shortage problem. They reported that short-term reservoir operation outcomes from the NSGA II methods increased hydropower production but only slightly affected water supply to the different stakeholders. Actually, their results were based on a short-term plan. Similarly, Zhang et al. [65] employed the technique on the Dahuofang Reservoir, Hunhe River, China, to optimize the trade-off changes and to minimize water shortage. Chu et al. [66] used NSGA II on the inter-basin connected reservoirs called Dahuofang, Guanyinge, and Shenwo in China. The other type of heuristic method used was GA. This technique is discussed in four publications. For instance, Xu, Q et al. [67] applied GA to the Heihe River Basin, China, to reduce the water shortage for the different stakeholders. Hu et al. [68] implemented GA in the Qujiang River basin China. Lai [69] used GA to solve the water shortage in China. Fowe et al. [70] applied a GA to address irrigation water shortage on the Boura reservoir, Burkina Faso.
Like heuristic methods, a number of different types of mathematical models are used to address water shortage allocation problems. For instance, interactive two-stage fuzzy stochastic programming (ITFSP) is used by Niu et al. [71] in a case study on the Hetao irrigation district, one of the largest irrigation districts for food production in China. They considered irrigation benefits, economic penalty, and irrigation quota as constraints to maximize agricultural system benefits through allocating the limited water to three main crops (i.e., wheat, maize, and oil plant). A dynamic model is implemented by Wang et al. [72] for optimal water distribution on the Heihe River Basin in the northwest of China and by Grafton et al. [73] on the Murray River of Australia. They used optimal quotas, drought status, weather condition, and storage status as criteria to maximize the net present value of water between extractions and in situ uses. Elmahdi and McFarlane [74] tested an integrated decision support system (DSS) on the Gnangara Groundwater System (GGS). That is a large aquifer situated in the southwest region of Western Australia. Their research employed different models together to maximizing recharge, maximizing biodiversity, maximizing short-term economic gains, maximizing food security, maintain zero abstraction for public water supply by considering quantitative indicators namely environment (e.g., climate, land uses, land management, status of river gauge or river reach) and socio-economic factors (e.g., policies). A MILP decision method was used by Roozbahani et al. [75] to solve transboundary water allocation problems to reduce water shortage to different stakeholders in the Sefidrud Basin, Iran. Later, they extended their work by introducing additional constraints that maximize the minimum water allocation ratio to the stakeholders [76]. Other types of mathematical models such as rule-based, inexact quadratic programming (IQP) and multi-objective based sum weighted method were used to solve water shortage problems by Song et al. [77], Cai et al. [78] and Shang [79], respectively.
In this segment, the multi-attribute decision method was rarely used. Alamanos et al. [80] employed four types of methods and compared their results, namely, multi-attribute utility theory (MAUT), analytic hierarchy process (AHP), elimination and choice expressing reality (ELECTRE), and technique for order of preference by similarity to ideal solution (TOPSIS). They optimized the water allocation problem of the Lake on Karla Watershed, located in central Greece. Lee M et al. [81] used a multi-attribute weighted method to minimize sever water shortage from excessive irrigation use of the Choshui river, Taiwan. One publication used both multi-attribute and multi-objective methods for feasible actions (alternatives) that can balance water supply-demand in the semi-arid region of northeast Brazil, i.e., PROMETHEE V and Integer linear programming (ILP) [82].
3.1.2. MCDM Methods Application to Solve Water Use Management Problems
Water use refers to the total amount of use of water by the ecosystem, for domestic purposes and agriculture, for energy production, and by industrial sectors [3,83]. It is essential to measure and evaluate the amount of water used by these different users. This leads to water use management. Water use management is defined as a process of planning, developing, distributing, allocating, and managing the optimum use of water resources [84]. Water use management endures the idea of optimum allocation of water resources by taking into account ecological, economic (including water price), and social functions [83]. In summary, water use allocation consists of a combination of policies, laws, and mechanisms to manage the distribution of water resources among competing uses. Modern water use management strategies should be robust by performing well under both average and extreme conditions. Moreover, it should be flexible and adjust to changing conditions over a time span [85]. At present, the issues of water resources management are addressed by considerations of any sectoral interference and trade-off [86]. This paradigm shift in water resources management is precisely the requirement of equitable distribution of water among users, the need for adequate governance, efficient and effective economic measures, and environmental performance. Optimal water use management is one of the fundamental objectives of water allocation research studies.
In this topic, 10 reviewed publications fall under multi-objective and one paper is categorized under a multi-attribute decision-making method, and one paper uses both methods. From the MODM class, the heuristic method NSGA II is the most predominantly employed decision method. Five publications use NSGA II to solve water use management problems. Hurford, Huskova, and Harou [87] applied the NSGA II method to generate optimal water management options that consider the benefits of all stakeholders on a multi-reservoir water system located on the Jaguaribe River, Brazil. They suggest optimum water use policies that incorporate economic, ecological, and livelihood dimensions. The results show an increase in allocated water to different downstream users. A similar decision technique method is used by Dai et al. [88]. They propose an optimal reservoir operation on the Three Gorges-Gezhouba cascade reservoirs in China. The proposed water management option will enable decision-makers to establish suitable reservoir operation rules. They come to the conclusion that NSGA II is an effective and recommendable method to optimize especially reservoir operations. The procedure is fast, flexible, and easy to accelerate sorting processes and compares individuals in a population [89]. The NGSA II method has an improved computational complexity convergence efficiency and model robustness [89]. Lewis and Randall [90] applied the technique to manage water for crop production at the Murrumbidgee irrigation area in Australia. They consider different constraints (i.e., available water, cultivated area, environmental flow, and groundwater pumping rate) to maximize net revenue, minimize groundwater pumping, and minimize variable costs. The result presented optimal water use for different crops under different scenarios that allocate land for each crop to maintain sustainability. Martin et al. [91] implemented NGSA II on the Goulburn-Broken River catchment, Victoria, Australia, to manage water distribution to different users. Yan et al. [92] employed the same method to identify and assess a robust water allocation plan for future water use of the Pearl River basin. Furthermore, different types of mathematical models are implemented to solve water use management problems, e.g., a multi-stage fuzzy stochastic programming (MFSP) is applied by Li C et al. [93] to solve complex water resource management problems in the northwest of China. Goal programming is applied by Li Yet al. [94] on the South-to-North Water Diversion Project in China; LP [95] is employed to analyze the trade-offs in the water–energy–-food nexus in Nepal and compound cloud model (CCM) to solve a water allocation problem in Nanjing [96]. In addition, a hybrid of TLFWM (mathematical model) and STLFCWM (mathematical model) is applied by Li M et al. [97] to allocate the limited water resources to different water users in the Northwest of China. Moreover, the STLFCWM model has a unique advantage over a TLFWM model since it addresses random uncertainty in the form of a membership function. The model can provide optimal water allocation plans under different flow levels. Another paper by Rousta and Araghinejad [98] used both MODM (Ideal point distance-based methods _TOPSIS) and MADM (SAW) methods to address water resources management of the Gorganrud River Basin in the north of Iran. In this part, only a single paper used the multi-attribute AHP technique to select the best reservoir to achieve sustainable water use for aquaculture development in Sri Lanka [99].
3.1.3. MCDM Method Applications to Solve Water Quality Problems
Water quality is defined as the condition of the water content with reference to the physical, chemical, and biological characteristics. It is expressed as the suitability of water for particular purposes like drinking, swimming, agriculture, and industrial demands [100]. The water quality is measured by analyzing many factors such as the concentration of dissolved oxygen (DO), salinity (TDS), heavy metals, nutrients, phosphorus, nitrate, ammonia, microorganisms, PH, water temperature, and the amount of suspended materials in the water (turbidity), etc. [101].Water quality level is determined by measuring the chemical and physical contents and then it has to be compared with the global standard. The water quality level ranges vary depending on the intended water use. The quality of water required for municipality purposes is different than the water quality level needed for industrial or agricultural activities. Good quality of water is crucial and required for humans, animals, and the environment. On the other hand, poor quality of water creates health risks and negatively affects the ecosystems. Water quality is significantly affected by wide ranges of natural and human influences. Natural factors that arise from geological, hydrological, and climatic conditions affect the quality of water. The amount and degree of influence are largely visible in the case of arid and coastal areas. Negative humans’ activities on top of environmental pollution enact a considerable role in deteriorating the water quality [102]. Wastes (pollution) from human activities (e.g., domestic, agricultural, industrial inputs) are the key reason for water quality decline in various parts of the world. Currently, human activity pollution constitutes a critical threat to water quality. For instance, when wastes from human activities are dumped into water sources (e.g., lakes, rivers), then water sources are polluted. This means it is contaminated by foreign substances so-called pollutants. These pollutants change the water use suitability, and it is harmful to organisms and the environment [103,104,105]. In general, the water quality status of a given water resource is assessed by thoroughly measuring and summarizing the data, then it is reported in the form of a water quality index (WQI). The water quality index represents a summary tool for reporting evaluated water quality conditions in numeric expression in an understandable manner to the public and decision-makers [106]. Many studies have implemented MCDM methods to minimize water quality problems in water allocation planning by considering conflicting multi-criteria.
With regard to water quality problems, 2 papers applied the MADM and 6 publications applied the MODM methods. From the MADM method class, both papers used AHP decision techniques. The AHP used by Martin-Ortega and Berbel [52] had as a target to find the best criteria (attribute) from the trade-offs between the attributes involved by a number of respondents. This would help to identify the best environmental benefits in the context of EU Water Framework Directives to improve the water quality of the Guadalquivir River which is located in the southern part of Spain. The other study by Li Y et al. [107] adapted AHP to select the optimum site for industrial wastewater discharge at the Luoyuan Bay coastal area in Fujian of China. The study aimed to provide alternative sites to minimize the threats of pollutants coming from industry discharges. With respect to the MODM method classification, 3 publications employed a heuristic type of decision methods like (e.g., NSGA II and bee colony) and 3 papers used mathematical models such as LP, inexact two-stage stochastic programming (ITSP), and a Fuzzy approach. Raei et al. [108] applied NSGA II on a hypothetical area to design an optimal in situ groundwater bioremediation system. NSGA was also used by Zmijewski and Wörman [55] to optimize the tradeoff between hydropower production and reduction of the transport of phosphorus in the reservoir network of the Dalälven River, Sweden. Another form of heuristic algorithm method called Multi-Objective Artificial Bee Colony-based optimization approach (MOABC) was applied to allocate water quality monitoring stations in the Great Fish River, South Africa [109]. They reported, the method performed well under the considered criteria for building water quality networks along the river basin. In their report, they suggested the MOBAC algorithm for further use in the field of water quality. This is because, MOABC is based on the principle of swarm-intelligence, searching the global optimal by escaping from local optima. It is a very useful method for the exploitation and exploration of these types of problems. One publication by Karterakis et al. [110] utilized a hybrid method by combining a mathematical LP and a heuristic method called differential evolution (DE). The aim of the paper was to develop an optimal groundwater pumping scheme that supplies adequate freshwater demand in coastal areas of the karstic aquifer in Crere, Greece, without deteriorating the quality of freshwater due to the seawater intrusion. Regneri et al. [111] applied fuzzy programming to solve the combined sewer overflow problem to the Haute-Sûre storage lake in Luxembourg. Furthermore, mathematical models like ITSP (inexact two-stage stochastic programming) were employed on the Yinema River basin in northeast China [112]. They reported that optimal water allocation strategies to the four water sectors would improve the water use and water quality in the Yinema River basin. The study suggested the ITSP approach as applicable and effective for the management of water resources and limiting water pollutants. However, this model did not consider decision risk uncertainties, different water sources, climate change influence on water availability, and wastewater treatment efficiency.
3.1.4. MCDM Methods Application to Solve Water Ecosystem Problems
Ecosystems consist of four primary components namely water, land (soil and rock), air, and biological organisms (plants and animals including humans). An ecosystem is interrelated and the interaction is complex. Forests, wetlands, and grasslands ecosystems play a role in the global hydrological cycle. The normal functioning of the ecosystem components is immensely important for the water cycle and essential for achieving sustainable water management. Water is a notable part of an ecosystem. The aquatic/water ecosystem refers to the water-based environment in which plants and animals interact with the non-living features of the water-based environment system [113]. A water ecosystem serves to replenish and purify water resources. It is very important for human and environmental well-being. However, the sustainability of the water ecosystem has been affected by human activities like agricultural expansion, deforestation, degrading wetland, marsh areas, and effluent discharges from industries and households to water bodies [114]. This has a negative impact on the natural hydrological (water) cycle and can pollute surface and groundwater resources. To overcome such embedded problems, an ecosystem management approach has been introduced. The ecosystem management approach has received strong attention at the international level after the concept of natural resources management came into the agenda of the United Nation Environmental Program. Ecosystem management represents an integrated approach to managing the healthy functioning of the diversified natural system to ensure the sustainability of ecosystem goods and services to human beings′ needs [115]. Ecosystem services and goods include necessary benefits for societal interest, i.e., allocation of energy production, clean air, and maintaining the nutrient cycle, and operational of the water cycle. Some studies estimated that 64% of the world′s wetlands have disappeared since 1990 and the percentage of loss is higher in Asia [116]. According to Reference [113], on a global scale, ecosystem services from wetlands are in decline in terms of the services they provide. From 1997–2011, between 4.3 USD and 20.2 USD, trillion per year worth of ecosystem services were lost due to land-use change [113]. Currently, a paradigm shift has taken place in recognizing ecosystem management as an integral part of integrated water resources management to more sustainable aquatic development [117]. Multi-criteria decision-making methods have been used to allocate water resources to maintain and sustain ecosystem services.
In this regard, all 5 publications adapted the multi-objective decision-making (MODM) method. Three papers used a heuristic algorithm (GA, GA, and NSGA II), and the other two employed mathematical models (dynamic programming and MOGM).Yang [118] developed a genetic algorithm to optimize water allocation from the Yellow River Delta, China, to meet the environmental flow requirement of the restored wetlands. The model result of water release coincides better with the ideal value plant community needs. The GA model is best suited and effective to optimize water distribution for ecosystem/ecological problems. GA was used by Akhbari and Grigg [119] to optimize water allocation from the San Joaquin River, California, USA, to satisfy the environmental needs of the surrounding region. They reported the GA model performed well in producing an optimal solution. The sensitive results are appreciated and accepted. Cioffi and Gallerano [120] studied the Pieve di Cadore reservoir (Piave River, Italy), using two different optimization methods to optimize water release for power production and fish habitat protection (aquatic ecosystem). They compared and analyzed the performance of the two models′ observational results, i.e., e-constraint and NSGA. The e-constraint method was first introduced by Haimes et al. [121].It keeps one of the objective functions to be optimized while the other objective functions are converted into constraints by setting an upper bound to each of them [121]. The e-constraint method is faster computationally and allows a direct sensitivity analysis of the solutions under constraints. On the other hand, the NSGA method is by far more informative than an e-constraint method (traditional method). Besides, it provides an option to examine the intermediate results of the optimization solution space.
Mathematical models are also often used to address the water problem with regard to ecological/ecosystem management. Lee [122] studied how to optimize the environmental and economic demands on the Tseng-Wen reservoir, Taiwan. He used the multi-objective game-theory model (MOGM) and e-constraint methods to analyze the conflicting interaction between economic development and environmental protection. They reported that MOGM is preferably used for environmental problems because it supports and permits a more realistic simulation of stakeholders’ preferences. Moreover, the model is suitable for providing a general planning and policy insight. Whereas, the e-constraint method focuses on either minimization or maximization of a specific environmental factor/objective of an optimization problem. Furthermore, sometimes the results of the traditional multi-objective optimization may not be feasible or socially acceptable. This leads to a failure to implement the strategy or policy. On the contrary, MOGM is flexible to find politically and socially acceptable compromises [123]. In general, with MOGM it is easier to incorporate socially sound choices for policymakers to realize into practice. The other type of mathematical models, called Feasible search discrete differential dynamic programming (FS-DDDP), was used to optimize reoperation of multi reservoirs for integrated water management to address the conflict interaction between water use and environmental deterioration of Nanpan River, China [124]. The results of the study showed that the model performs well in the optimal reservoir reoperation problem compared to routine reservoir operations. They suggested the model can be readily extended and applied to multi-reservoir water management systems.
3.1.5. MCDM Methods Application to Solve Flood Risk Problems
Flood is defined as an overflow of water that submerges land areas that are usually dry [125]. Flood originates from various sources like oceans, seas or rivers, and lakes. Flood is normally triggered by extreme rainfall events or heavy precipitation, e.g., by monsoon rains in Asia and the Indian peninsula, and snow melts due to rapid temperature increases (example in Northern hemisphere during spring season after strong winter snowfall, this occurs when the season changes from winter to spring, it results in a slight temperature change) which causes an increase in river flows and elevation. Further, a flood also occurs when intensive long-duration rainfall happens during autumn that is when summer ends. A flood occurs when manmade dams fail due to many unpredictable causes like landslides, technical errors, or volcanic eruptions and earthquakes. Recently, flooding has remained a recurrent phenomenon in coastal and estuarine sea areas of the world due to extreme atmospheric depressions (e.g., cyclones, typhoons, and hurricanes). Flooding results also from sea level rise and natural events of an earthquake volcanic eruption (e.g., tsunami tidal waves) which causes massive volume of water displacement from oceans or sea to land areas [125]. Flood has a negative impact on infrastructures, damaging homes, community and agricultural production, and natural biodiversity. Moreover, it might risk human health if the water is exposed to pollutants. The extent and the magnitude of the impact depend on the nature and occurrence of the flood in a given region. Flood management includes both operational and administrative activities that have been taken before, during, or after the occurrence of flood events to mitigate or prevent flood impacts on the socio-economic and environmental resources. As part of flood operational management, reservoir water allocation is considered a flood controlling mechanism. Flood is one of the worst natural hazards affecting the life of people. For example, between 2000–2014, more than 85,000 human fatalities occurred and affected about 1.4 billion people around the globe [5]. Therefore, flood risk management is important and it requires the use of multi-criteria decision-making methods that consider multiple objectives, constraints, trade-offs, and feasible alternatives.
This section point out the evaluation of an MCDM application specifically aimed at flood release control of reservoirs. Extreme events of river flow and high reservoir storage result in an overflow of water and have negative consequences on wealth and human beings if a flood disaster occurs. It is important to minimize and mitigate the impacts of the flood by controlling reservoir operations and regulating the river flow. However, reservoir flood operations, especially cascade reservoirs, are complex and challenging for water resources planners and decision-makers. Hence, the objectives of flood operation in the case of multi-reservoir systems are complex, due to conflicting interests among different objectives. For example, water releases from a reservoir may be required to maximize hydropower generation, at the same time as releases need to be restricted to minimize flooding at downstream river reaches. Jia et al. [126] adapted and implemented the multi-objective best compromise decision model called (MoBCDM) on the Shiguan River basin (consists of two reservoirs, three flood control points, and two flood routing river reaches) to improve the optimal flood operation practices of frequently changing the opening of flood gates in central China. The model is composed of a utility function for a quantitative preference comparison, fuzzy analytic hierarchy process (FAHP) for assigning weights, DE for an optimization algorithm, and segmentation and averaging Seg/Ave for a feasible floodgate operation. They considered four historical flood operations scenarios to test the model. The results prove, the MoBCDM outperforms well in all reservoir operation scenarios in reducing peak flow at flood control points when validated to the observed reservoir rule operation. Moreover, this model has interacting features in considering decision-makers′ preference information. However, the flexibility and efficiency of the model have not been tested when the system dimensions size increases like when a number of reservoir and control points increases. The detailed criteria and objectives list used in the model analysis are presented in Supplementary Material Table S1.
3.1.6. MCDM Methods Application to Solve Combined Water Problems
Water Shortage and Water Quality Problems
MCDM has been extensively applied to support decision-making processes for issues related to water quantity and quality. Multi-criteria decision tools are preferably applied to address combined water problems. It is an effective tool and especially after mid-20th century, MCDM has been successfully used to select optimal strategies to reduce water shortage and water quality problems, supporting to optimize the allocation of water resources [127]. In recent decades, water quantity and quality problems represent a hot topic agenda. WHO [128] reported that more wastewater is generated and dispersed today than ever in the history of our planet. Around 1.1 billion people lack access to safe drinking water and 1.8 million people die from diarrheal disease each year. Water allocation to solve water shortage and water quality problems is essential for decision-makers because combined water problems have a significant impact on the environment and socio-economic development of society.
This part underlines and discusses a combination of water shortage and water quality problems. In some cases, water is allocated to address both water problems. The degradation of water quality has a significant consequence, water becomes unfit for use and the water quantity availability is reduced. Often, the MCDM method is applied to tackle combined water problems of water quantity and quality. In this case, both multi-attribute decision-making and multi-objective decisions-making tools were used namely ELECTRE II, Fuzzy, and LP, respectively. Yang et al. [129] employed the ELECTRE II and AVF (Additive value function) methods to prioritize water management alternatives based on the DPSIR framework (Driving force-Pressure-State-Impact-Response). The research was applied to the Anyangcheon watershed in South Korea to examine the water allocation problem of the watershed, which has already suffered from potential streamflow depletion and possible water quality deterioration [130]. Their research improved and modified the set of criteria used earlier by Reference [131]. The criteria selected have mainly focused on satisfying the demands on water quality and quantity need. The result report shows that AVF is easy and convenient to be used. However, ELECTRE II is more effective and it shows the outranking priorities of the alternatives. This indicates that the ELECTRE method is an ideal tool for prioritizing alternatives with respect to water quality and quantity problems. However, they did not consider the impact of water price on the decision-making process and also used only limited water pollutant materials for determining the characteristics of the mining sites. Hence, in the future, these components ought to be underlined for optimal water management strategies. The other form of multi-attribute decision making used is modified fuzzy social choice (MFSC). This method was applied by Pourmand and Mahjouri [132]. The objective of the study was to find a socially optimal scenario for water allocation and reuse in Tehran, Iran. There has been a growing concern about the increase of water demand and pollution by wastewater from the agricultural and industrial sectors. To address the existing water allocation problems, they proposed scenarios for the water quantity and quality management by considering multi-stakeholders’ conflicting utilities, negotiation power, degree of importance, and uncertainties. Eventually using the MFSC method, socially acceptable scenarios were prioritized to address water allocation problems of Tehran city. In their result analysis, the MFSC method has some advantages like its flexibility in defining preferences and incorporating imprecise input information using fuzzy membership functions. The method requires less mathematical calculations. However, they did not include uncertainties associated with water availability and reclaimed wastewater.
From the MODM class, LP was applied by Ke et al. [133] to optimize water allocation in Ordos city, China, by considering water quantity and water quality aspects of the Ordos river. The quality had been affected by mining industries. The LP method is used to address water allocation with reference to water quantity and to reclaim polluted water. They discussed that the dynamic linear optimization model can elaborate and simultaneously address problems related to water shortage and water quality.
In summary, mathematical programming (LP) was predominantly employed to address combined water problems. ELECTRE II and MFSC were preferably used to prioritize multi-attribute water management alternatives.
Water Shortage and Flood Problems
As discussed in the intergovernmental panel on climate change IPCC [134] assessment report, arid and semi-arid areas are particularly exposed to the impacts of climate change on water resource availability. This creates temporal and spatial variability in water resource distribution particularly in, e.g., Mediterranean Basin, western United States, and major parts of Africa, northeast Brazil, southern and eastern Australia. There is a discrepancy in water uses and users. Therefore, water resource management is crucial to satisfy the demand–supply relationship. Since the flow of a river is highly dependent on the seasonal climatic variation, it drives water managers to harvest water during the wet season to minimize water shortage during the dry season. One of the water resources management strategies is building water resources structures along a river basin such as dykes and reservoirs to store water [135]. However, it has been very challenging to optimally control reservoir water operations for water resource planners and managers. When the reservoirs get sufficient water supply in a wet period, then it is possible to control the water level to minimize flood risk to downstream areas. In normal periods of reservoir operation, all planned demands are met, the reservoir storage level is kept at or above the intended level. While during dry periods, when the reservoir storage level falls, the reservoir release is reduced to maintain a sufficient amount of water remaining in the reservoir for future water supply. This kind of situation seeks appropriate multi-criteria decision-making methods to optimally solve the existing conflicting trade-offs objectives, meeting ongoing water users′ demand, minimizing flood risks, and ensuring adequate reservoir storage when inflow is insufficient [136]. The MCDM methods are useful in situations where there is a decision-making that must meet multiple objectives in an integrated manner [135].
More often optimization is applied in reservoir water resource allocation to address a combined water shortage and flooding problem. Veintimilla-Reyes et al. [137] developed a generic linear programming model to optimize water allocation from a networked reservoir system to meet multiple spatially and temporally distributed water demands, reducing flood from maximum capacity and minimizing costs associated with unmet demand and flood events. The report shows that the LP model effectively optimizes the spatiotemporal allocation of water on a connected reservoir system. They suggested the model can be extended by considering other additional parameters like identifying new optimal locations for additional reservoirs.
This entry is adapted from the peer-reviewed paper 10.3390/w13020125
