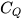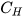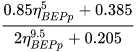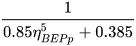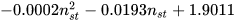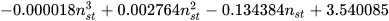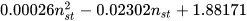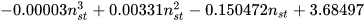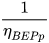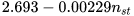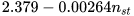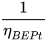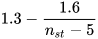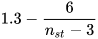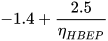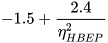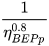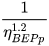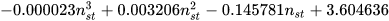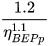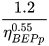Pumps As Turbines (PATs) are reverse-running pumps and their use can be the best solution for exploiting small hydraulic resources. Pump manufacturers do not provide the performances of their machines running in reverse mode, thus several authors developed appropriate prediction models. Some of them can only correlate the pump Best Efficiency Point (BEP) to the PAT corresponding one; other ones are able to obtain the characteristic curves. In this paper, a review of these methodologies is presented with the aim to find the best strategy that allows a designer of a small hydropower plant to select the PAT to be used and to predict its characteristic curves. The study also highlights the possibility of disassembling some models in order to merge the best parts in a more reliable strategy.
- pump as turbine
- PAT
- hydropower
- characteristic curves
1. Introduction
Pumps running in reverse mode, Pumps As Turbines (PATs), can be effectively used for exploiting small hydraulic resources, with the main advantage of being cheaper than traditional hydraulic turbines [1]. Other favourable aspects can be found in the wide presence of pump manufacturers all around the world, with spare parts easily available. Moreover, pumps are technologically simpler than hydraulic turbines, thanks to the lack of a flow control system [1].
PATs can be found in different plants with the aim of producing electrical energy, for example reverse-running pumps can substitute Pressure Reducing Valves (PRVs) in Water Distribution Networks (WDNs) and in irrigation systems, as reported by various authors [2,3,4,5,6,7,8,9]. Pumps running as turbines can also be used in industrial plants such as oil refineries [10] or to recover energy from rainwater [11]. Furthermore, it is possible to use PATs in Pumped-Hydro Energy Storage (PHES) systems, not only in high power plants, but also in micro-hydropower ones [12,13].
Renewable energy sources can be the best solution in order to meet the need for electricity in developing countries and hydraulic energy is the one characterized by the lowest cost [14]. In this regard, Arriaga [15] and Motwani et al. [16] analysed the possibility of using PATs, respectively in Laos and India, reporting favourable aspects.
The main hindrance of using PATs is the lack of information related to their performances, which is not provided by pump manufacturers [1]. For this purpose, several authors developed models that belong to two main macro-approaches: Basic model that can correlate pump Best Efficiency Point (BEP) to the PAT one and models that can predict the characteristic curves of a PAT.
For exploiting small hydraulic resources using a PAT, two main problems arise: The selection of the PAT to be used and the prediction of the PAT characteristic curves. Concerning the first problem, basic models can be effectively used, starting from the hydraulic resource information [7,8]. The calculation of PAT characteristic curves requires more complex models and allows the identification of the operating point, necessary to estimate the producibility of the hydropower plant [7,8].
In this paper a review of the most important and recent methods used for predicting PAT performance is displayed, with the main objective of aiding the designer of hydroelectric plants suitable for the use of PAT. First, the various methods are briefly described focusing on the key points, then the study analyses their advantages and drawbacks. A global methodology has the aim of selecting the PAT, reconstruct the geometry and obtaining the characteristic curves. Even if various authors provided original contributions regarding these three modules, models could usually obtain good accuracy for a PAT, but are not able to work properly on another one. Therefore, in this paper the authors analysed the possibility of disassembling the methods in modules and merge the best ones to create a new strategy with better reliability.
2. PAT Modeling Approaches
In order to obtain information about the performances of a PAT, appropriate methods have been developed by various researchers and can be found in the literature.
Several authors, listed in the following, proposed basic models that allow the most suitable PAT to be identified for a given site: Alatorre–Frenk [17], Algieri et al. [9], Barbarelli et al. [11], Childs [18], Derakhshan and Nourbakhsh [19], Grover [20], Hancock [21], Hergt [20], Sharma [20], Schmiedl [20], Stefanizzi [22], Stepanoff [20] and Yang et al. [23]. These methods are based on the calculation of two conversion factors CQ and CH expressed by Equations (1) and (2) [1].
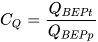 (1)
(1)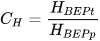 (2)
(2)From the above equations, it is easy to observe that CQ is the ratio between PAT and pump flow rate at BEP, as well as CH is the ratio between PAT and pump head at BEP [1].
These two conversion factors can be used for the preliminary selection of the machine to be installed. In fact, knowing site flow rate Qsite = QBEPt and site head Hsite = HBEPt and calculating the conversion factors it is possible, by means of inverse formulas, to obtain QBEPp and HBEPp related to the pump and necessary to use the manufacturers’ catalogues [7,8].
Obtaining the characteristic curves of a PAT, is highly important to identify the operating point of the machine coupled with a given hydropower site. Methodologies that can predict the characteristic curves of a PAT can be classified as follows:
- Empirical models
- 1D models that recreate the unknown geometry of the machine
- 1D models that use a known geometry
- 2D models
- 3D-CFD (Computational Fluid Dynamics) models
2D models are rare because the flow field is not characterized by particular symmetries and they are only cited in this paper. In fact, the hypothesis of a two-dimensional flux can be considered valid only for low specific speed turbomachines with radial flow [24]. Nevertheless, 2D models can be used for obtaining correlations that allow the slip factor to be calculated [25].
3. Basic models
As discussed in the previous section, these models are based on the calculation of two conversion factors CQ and CH, usually expressed as a simple function of pump parameters (pump efficiency at BEP, ηBEPp and pump hydraulic efficiency at BEP, ηHBEP) or PAT parameters (PAT efficiency at BEP, ηBEPt and PAT specific speed, nst) [20,21]. These kinds of correlations are reported in Table 1.
Table 1. Basic models correlations for the calculation of the conversion factors [9,11,17,18,20,21,22,23]
|
Model |
|
|
|
Alatorre–Frenk |
|
|
|
Algieri et al. |
|
|
|
Barbarelli et al. |
|
|
|
Childs |
|
|
|
Grover |
|
|
|
Hancock |
|
|
|
Hergt |
|
|
|
Schmiedl |
|
|
|
Sharma |
|
|
|
Stefanizzi |
- |
|
|
Stepanoff |
|
|
|
Yang et al. |
|
|
4. Model that Predict the Characteristic Curves of a PAT
This chapter regards the description of some of the most important methods of the following categories: empircal models, 1D models and 3D-CFD models.
4.1 Empirical Models
Empirical models allow the characteristic curves of a reverse-running pump to be obtained using polynomials derived from a statistic analysis of experimental data, with the aim to have a universally valid method. In this study, the authors considered the method proposed by Derakhshan and Nourbakhsh [19] as representative of empirical models because, even if several authors [11,26] developed models of this typology, they are similar to each other. In particular, the methodology proposed by Derakhshan and Nourbakhsh [19] is based on experimental data obtained by the same authors testing four centrifugal pumps, using a purpose-made test rig. In particular, the specific speed of the machines selected is included in the range 14–56. The authors referred to dimensionless parameters for flow rate, head and power defined by Equation (3) [19].
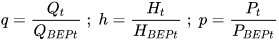
The correlations proposed by Derakhshan and Nourbakhsh [19] to obtain the characteristic curves of a PAT are reported in the following equations:
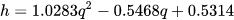
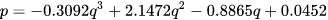
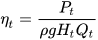
4.2 1D Models That Recreate the Goemetry of the Machine
Several authors such as Barbarelli et al. [27] and Manservigi et al. [28] proposed one-dimensional models able to recreate the unspecified geometry of the machine, starting from data that can be found in the catalogues provided by pump manufacturers. In a such way, it is possible to obtain a better prediction accuracy in comparison with empirical models, without restricting the scope of the method.
The first step of the model proposed by Barbarelli et al. [27] includes defining a simplified geometry, starting from the following data, which can be found in the manufacturer’s catalogues:
- Pump head at BEP
- Pump flow rate at BEP
- Maximum power
- Head at zero flow
- Impeller diameter
- Size of the pump
Geometry is reconstructed using standard rules usually followed by pump manufacturers, but, if it is known, the real geometry of the machine can be used [27]. The second part of the model consists of an iterative procedure necessary to identify the value of the volumetric efficiency and involves the calculation of hydraulic losses divided into friction losses Zf and dynamic losses Zd expressed by the authors by means of Equations (7) and (8) [27].
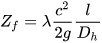
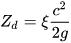
Compared to the study previously proposed by Amelio and Barbarelli [29], the main difference is the addition of a loss related to low flow rates. By means of this iterative procedure the head curve is obtained:
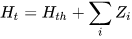
Barbarelli et al. [27] also proposed the calculation of the other performance curves. To obtain the efficiency curve, in parallel to volumetric efficiency, hydraulic efficiency ηH and disc efficiency ηD are needed, as reported in the following equation:
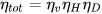
Finally, Equation (11) can be used to calculate the power curve.
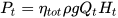
Manservigi et al. [28] proposed a model capable of calculating the characteristic curves of a PAT, starting from the ones related to the pump. This model is based on an iterative procedure with the aim of optimizing the value of 24 parameters, 14 of them related to the pump, the other 10 related to the PAT. These parameters refer not only to the geometry of the machine, but also to hydraulic and power losses and some of them relate the BEP of the PAT to the pump corresponding one.
In particular, regarding the PAT physical modelling, proposed by Manservigi et al. [28], starting from the theoretical head, the real head of the PAT is known adding the hydraulic losses, as expressed by Equation (9). The power curve can be obtained considering hydraulic efficiency ηH, flow rate Qt, leakage flow rate Ql and power losses L using the following equation:
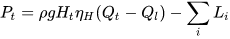
The efficiency curve can be easily obtained by means of Equation (6). Pump performance curve obtained using the model are compared to the ones provided by pump manufacturers through the parameter Root Mean Square Relative Error (RMSE), defined by the authors as:
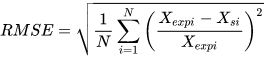
where Xexp and Xs refer to experimental and simulated values, respectively, and N is the number of values available. The optimization procedure minimizes the sum of RMSEs for the performance curves to find the optimal values of the 24 parameters, thus, to reconstruct pump and PAT performance curves. Moreover, the optimization procedure can regard direct and reverse running mode separately or simultaneously [28].
4.3 1D Models That Use a Known Geometry
One-dimensional models based on a known geometry are developed with the aim of obtaining more accurate predictions related to methods that recreate a simplified geometry of the machine. Stefanizzi et al. [30] proposed a method belonging to this typology, that can be, as the authors suggest, a reliable tool for pump manufacturers that want to better know the reverse running behaviour of their machines. In fact, the complexity of this method is too high to consider it intended for a designer of a small hydropower plant. The first step of this methodology consists of collecting detailed geometrical information of the machine, and then establish the flow rate Qt and the rotational speed nt related to the PAT. This is required to obtain the velocity triangles, in particular the circumferential components of the absolute velocities c2u and c1u. Thanks to the previous step, it is possible to calculate the theoretical head using Equation (14) and, subsequently, to obtain the real head of the PAT, taking into account hydraulic losses in the volute Zv and in the impeller (runner) Zr, using Equation (15).
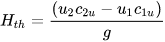
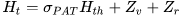
Moreover, Stefanizzi et al. [30] also considered a correlation for a slip factor σPAT, obtained by Capurso et al. [31] by means of a CFD analysis and reported in Equation (16).
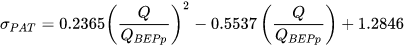
4.4 3D-CFD Models
Three-dimensional models based on computational fluid dynamics concerning PATs are being used in different ways, as discussed in the following. Frosina et al. [32] developed a model to analyse the behaviour of three commercial pumps with different specific speeds running in direct and reverse mode. Perez–Sanchez et al. [33] proposed a 3D-CFD model to study the behaviour of a reverse-running pump used to reduce pressure in a WDN. Moreover, several authors like Yang et al. [23], Rossi et al. [34] and Stefanizzi et al. [30] used computational fluid dynamics for validating models of the typologies previously described. Finally, Li [35] used computational fluid dynamics to analyse the behaviour of PAT characteristic curves considering water and four different types of viscous oils, thus considering fluids with different kinematic viscosity.
5. Discussion
PATs can be effectively used for exploiting small hydraulic resources, but it is important to have information on their performances to properly select the machine to be used and to obtain the operating point. To this end, basic models and methods able to predict PAT characteristic curves are needed.
Basic models which correlate the conversion factors CQ and CH to PAT specific speed, can be immediately used for the selection of the machine. In fact, by knowing head Hsite = HBEPt and flow rate Qsite = QBEPt related to the hydraulic resource, as well as the PAT rotational speed, it is possible to calculate the required PAT specific speed nst. Using the conversion factors is possible to calculate the pump corresponding parameters (QBEPp and HBEPp), thus the machine is selected from manufacturer’s catalogue. From this point of view, it is easy to use the models proposed by Algieri et al. [9], Barbarelli et al. [11], Derakhshan and Nourbakhsh [19], Grover [20], Hergt [20] and Stefanizzi [22]. This aspect is underlined in Table 2, in which the possibility to apply the model starting from site data is remarked with the symbol ∗. Moreover, Table 2 highlights the output of basic models as well as the kind of analysis from which the correlations derive, namely theoretical considerations or experimental data.
Table 2. Basic models characterization [9,11,17,18,19,20,21,22,23].
|
Model |
Use of Site Data |
Output |
Based on |
|||
|
CQ |
CH |
ηt |
Theoretical Considerations |
Experimental Data |
||
|
Alatorre–Frenk [17] |
- |
∗ |
∗ |
∗ |
- |
∗ |
|
Algieri et al. [9] |
∗ |
∗ |
∗ |
- |
- |
∗ |
|
Barbarelli et al. [11] |
∗ |
∗ |
∗ |
∗ |
- |
∗ |
|
Childs [18] |
- |
∗ |
∗ |
- |
∗ |
- |
|
Derakhshan and Nourbakhsh [19] |
∗ |
- |
|
- |
- |
∗ |
|
Grover [20] |
∗ |
∗ |
∗ |
- |
- |
∗ |
|
Hancock [21] |
- |
∗ |
∗ |
- |
∗ |
- |
|
Hergt [20] |
∗ |
∗ |
∗ |
- |
- |
- |
|
Schmiedl [20] |
- |
∗ |
∗ |
- |
- |
- |
|
Sharma [20] |
- |
∗ |
∗ |
- |
∗ |
- |
|
Stefanizzi [22] |
∗ |
- |
∗ |
- |
- |
∗ |
|
Stepanoff [20] |
- |
∗ |
∗ |
- |
∗ |
- |
|
Yang et al. [23] |
- |
∗ |
∗ |
- |
∗ |
∗ |
To identify the operating point of a PAT it is necessary to use methods able to predict its characteristic curves. This study highlighted the possibility of a model that predicts PAT characteristic curves to be based on experimental data, theoretical considerations or CFD. This aspect, in parallel to input and output of the methods reviewed, is reported in Table 3, where the symbol ∗ means, once again, the presence of a factor for the considered model.
Table 3. Characterization of models that predict the characteristic curves of a PAT [19,27,28,30,32,33].
|
Model |
Input |
Output |
Based on |
|||||
|
Pump BEP |
Catalogue Information |
Machine Geometry |
Characteristic Curves |
Flux Lines |
Experimental Data |
Theoretical Considerations |
CFD |
|
|
Derakhshan and Nourbakhsh [19] |
∗ |
- |
- |
∗ |
- |
∗ |
- |
- |
|
Barbarelli et al. [27] |
∗ |
∗ |
- |
∗ |
- |
- |
∗ |
- |
|
Manservigi et al. [28] |
∗ |
∗ |
- |
∗ |
- |
- |
∗ |
- |
|
Stefanizzi [30] |
- |
- |
∗ |
∗ |
- |
- |
∗ |
- |
|
Frosina et al. [32] |
- |
- |
∗ |
∗ |
∗ |
- |
- |
∗ |
|
Perez–Sanchez et al. [33] |
- |
- |
∗ |
∗ |
∗ |
- |
- |
∗ |
Methods able to predict PAT performance curves starting from data found in pump catalogues are the ones useful for a small hydropower plant designer. Thus, the focus of this discussion regards empirical models and 1D models that recreate the PAT geometry.
These models can obtain good results for a machine, but cannot be properly applied to other PATs. This is a common problem in PAT performance predicting models, but it is possible to consider the advantages of the various methods and to unite them obtaining a more reliable strategy.
Empirical models, as the one proposed by Derakhshan and Nourbakhsh [19], are simple to apply, but they are seldom robust and are valid in a limited range of the specific speed of the machine.
The one-dimensional model developed by Barbarelli et al. [27] presents a detailed modelling of dynamic losses and a wide range of application. Its main drawback is the improvable geometry reconstruction.
The advantage of the model proposed by Manservigi et al. [28] is the geometry reconstruction by means of an optimization procedure but the result is dependent on hydraulic losses modelling, considered by the authors in a simplified way.
Future developments may involve disassembling these methods to consider the best parts of each, with the aim of combining them and creating a new tool, more reliable but not more complex. In this regard, it seems possible to combine the optimization procedure for the geometry reconstruction proposed by Manservigi et al. [28] with the detailed model of hydraulic losses proposed by Barbarelli et al. [27].
6. Conclusions
In this paper a review of methods used for selecting PATs and predicting their characteristic curves has been presented. The models developed by several researchers have been described and, after that, advantages and drawbacks have been analysed. The aim of the study was to provide information useful for a designer of a small hydropower plant, who wants to use a PAT, in selecting the proper machine and obtaining the operating point.
Basic models, able to correlate pump BEP to the PAT corresponding one, can be used for a preliminary selection of the machine. In particular, models which calculate the conversion factors CQ and CH as a function of the PAT specific speed seem to be the most suitable in this regard.
Obtaining the PAT operating point is crucial in the estimation of the produced energy, thus models able to predict PAT performance curves are required. Various approaches have been used to this purpose, namely empirical model, 1D models (with known geometry or able to reconstruct it), 2D models and 3D-CFD models. 2D models are considered as a valid tool to calculate correlations for the slip factor of turbomachinery and were not analysed in this study.
1D models that require a known geometry and 3D-CFD models were considered prohibitive for a small hydropower plant designer due to the complexity and computational expense. The methods able to predict PAT performance curves starting from data found in pump catalogues are the empirical models and 1D models able to reconstruct the machine geometry. Empirical models are simple but usually not robust, thus the study focused on the models proposed by Barbarelli et al. [27] and Manservigi et al. [28] as a sample of one-dimensional models that reconstruct PAT geometry. The study highlighted the possibility to disassemble these two models and to merge their best parts with the aim to obtain a more reliable strategy.
This entry is adapted from the peer-reviewed paper 10.3390/en13236341