You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Archard’s wear law is among the first and foremost wear models derived from contact mechanics that relates key operating conditions and material hardness to sliding wear through a multifaceted wear coefficient. This entry explores the development, generalization, and critique of the Archard model—a foundational model in wear prediction. It outlines the historical origins of the model, its basis in contact plasticity, and its use of a constant wear coefficient. The discussion highlights modern efforts to extend the model through variable exponents and empirical calibration. Key limitations such as the oversimplification of wear behavior, exclusion of factors like sliding velocity, and scale sensitivity are examined through both theoretical arguments and experimental evidence. The critiques reflect the model’s constrained applicability in diverse wear conditions across varied operating conditions and material phenomena.
- wear
- Archard’s wear law
- wear data
- wear modeling
The study of wear modeling has a long and extensive history. In 1995, it was thought that wear modeling was largely unorganized; Professor Ludema and his then graduate student Meng [1] conducted an extensive review covering the work of over 5000 authors who published with Wear and Wear of Materials conferences between 1957 and 1992. They reported that there was nearly no repetition of models yielding 182 distinct equations, which collectively involved over 100 unique variables and constants. Despite the many models stemming from similar theoretical foundations and approaches—including empirical observations, basic contact mechanics and material failure theories—there was no consistent structure among the resultant formulas. Nevertheless, one of the earliest models, known as Archard’s wear law, has remained one of the most prominent approaches to estimating wear [2]. Archard’s model, developed following earlier contributions by Holm [3], proposed that wear volume is proportional to the applied load (L) and the sliding distance (s) and inversely proportional to the material hardness (H), as seen in Equation (1), where V represents the total wear volume.
The above adhesive wear law can be derived following the details stated by Halling [4] and Figure 1. The wear volume per sliding distance 𝑄=𝑉/𝑠 for n spherically shaped asperities approximates from the worn volume as a half sphere, 𝑄=𝑛(2/3𝜋𝑟3)/2𝑟=𝑛𝜋𝑟2/3, which is proportional to contact area A. If p𝑚 is the yield pressure, or hardness, then the normal load is 𝐿=p𝑚𝐴=p𝑚𝑛𝜋𝑟2. Therefore, the wear volume per sliding distance is 𝑄=𝐿/(3p𝑚). Given that not all contacts produce wear, and not all asperities wear at the same rate, the wear coefficient is introduced to yield Equation (1). Originally introduced for adhesive wear, the equation has also been shown to be applicable to simple abrasive wear [4][5][6]. Further applications have extended to fretting and oxidative wear by slightly adjusting the model to include the hardness of the tribologically altered surface layer formed during wear [7]. Given its foundational role and continued relevance, Archard’s equation deserves a reevaluation using modern analysis techniques.
Figure 1. Illustration of asperity contact under applied load L and resulting approximation of wear volume depicted by the red shaded region within the dashed contact radius.
The proportional relationship expressed in Equation (1) relies on a dimensionless factor known as the wear coefficient, symbolized as k. This coefficient carries multiple interpretations. It reflects the following:
-
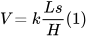
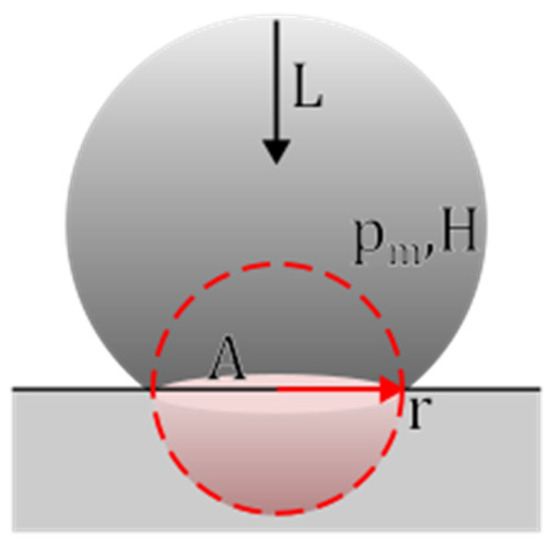
The geometric transformation from original surface asperities to the plastically deformed contact area that generates wear;
-
The relationship between yield strength and hardness;
-
The fraction of plastic deformation that contributes to material loss;
-
The likelihood that material can be removed from the contact interface;
-
The contributions of other factors (e.g., temperature, surface tribochemical activities, lubrication, etc.) not explicitly included by Equation (1) but empirically linked to wear.
While aspects (i) through (iii) can be linked to measurable properties of geometry and materials, they also involve stochasticity that warrants caution when used as a relative metric for wear resistance across materials. Differences in shape or in how a material’s yield strength relates to its hardness can affect the coefficient independently of any actual wear damage. In some instances, such as in point (iii), plastic deformation may occur without apparent material removal, resulting in measurable volume loss that does not constitute true wear. Conversely, purely elastic asperity deformation should not yield any apparent wear volume despite nonzero operating conditions; this case forces 𝑘=0, which may be a special case of Equation (1). Element (iv) touches on a more deterministic aspect of the model in statistical estimation of adhesive wear coefficients by integration of distribution of asperity critical junction sizes [8]. However, most wear models still rely on probabilistic approaches, especially when considering wear mechanisms beyond adhesion. Overall, the wear coefficient serves as a catch-all (v) for various relationships and is therefore highly variable.
Archard and others noted a direct proportionality between the applied load and the real area of contact when the latter is subjected to full yielding. Sliding speed was also considered a tightly controlled condition in many experiments [2]. If the velocity and contact area are assumed to remain constant, Equation (1) can be transformed into a rate-based model, shown in Equation (2), where the load is replaced by interfacial pressure (p) and sliding distance by velocity (u). This form, which effectively is derived via dividing Equation (1) by the contact area and taking a time derivative, expresses the rate at which wear depth (dr/dt) increases. However, this version for instantaneous wear should be applied carefully. In many wear tests, pressure does not remain constant, especially when significant wear has occurred. As a wear track develops, the contact area may increase, which would in turn reduce the pressure under the same applied load.
Following the work by Delaney et al. [9], this entry aims to garner a deeper understanding of Archard’s law via a systematic review on the theoretical foundations, extended forms, and known limitations of the model. In doing so, attention is drawn to the careful considerations one must account for when using Archard’s law for wear characterization or prediction. Modern approaches, such as machine learning, multifield modeling, and energy-based frameworks, are discussed as future directions for improved accuracy. Moreover, this entry discusses Archard’s law and its applications to typical cases of wear.
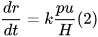
This entry is adapted from the peer-reviewed paper 10.3390/encyclopedia5030124
References
- Meng, H.C.; Ludema, K.C. Wear Models and Predictive Equations: Their Form and Content. Wear 1995, 181, 443–457.
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988.
- Holm, R. Electric Contacts; Almquist and Wiksells: Stockholm, Sweden, 1946.
- Halling, J. Principles of Tribology; The Macmillan Press LTD: London, UK, 1975.
- Timsit, R.S. Course on Performance and Reliability of Power Electrical Connections. In Electrical Contacts: Principles and Applications; Slade, P.G., Ed.; CRC Press: Boca Raton, FL, USA, 2014.
- Wang, Q.J.; Chung, Y.-W. Encyclopedia of Tribology; Springer US: New York, NY, USA, 2013.
- Liu, Y.; Liskiewicz, T.W.; Beake, B.D. Dynamic Changes of Mechanical Properties Induced by Friction in the Archard Wear Model. Wear 2019, 428, 366–375.
- Molinari, J.; Aghababaei, R.; Brink, T.; Frérot, L.; Milanese, E. Adhesive Wear Mechanisms Uncovered by Atomistic Simulations. Friction 2018, 6, 245–259.
- Delaney, B.C.; Wang, Q.J.; Aggarwal, V.; Chen, W.; Evans, R.D. A Contemporary Review and Data-Driven Evaluation of Archard-Type Wear Laws. Appl. Mech. Rev. 2025, 77, 022101 .
This entry is offline, you can click here to edit this entry!