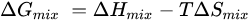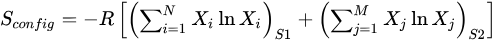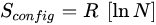Throughout recorded history, individuals have melded metals to enhance various physical attributes in them like strength, durability, ductility, conductivity, and luster. The exploration of alloys can be traced back to ancient times, approximately 2500 BCE, when the fusion of copper and tin gave rise to the creation of bronze. Noteworthy alloys such as bronze, brass, and steel share a common characteristic—they are comprised of a predominant element (copper for bronze and brass, iron for steel) that is blended with trace amounts of other elements like tin in bronze or carbon in steel. The modest proportions of additional elements in most alloys are emblematic of conventional alloying practices and are typically controlled during the synthesis process. Traditionally, during alloying, the added elements substitute an atom of the predominant element at the lattice position. Many contemporary alloys consist of a primary element, with supplementary elements incorporated at lower concentrations. For example, in the case of 6061 aluminums, Al constitutes 98.56%, with Mg and Si as the next highest concentrations. High-entropy alloys (HEAs), in contrast, exhibit a near-equimolar composition, comprising five or more elements, with no single element dominating the composition. This positions the composition toward the center of the phase diagram, departing from the conventional placement at the periphery that is seen for traditional alloys. The absence of any one element as the majority in the composition stands out as a key distinction between traditional alloy systems and high-entropy materials (HEMs).

An alternative method for discerning between traditional and high-entropy systems lies in their crystal structure. In traditional alloys’ unit cell, the predominant element is typically encircled by either similar predominant elements or by single atoms of elements that are present in lower concentrations. Conversely, a high-entropy unit cell with an equimolar composition of five elements in the crystal structure will likely have its closest neighboring atoms be dissimilar atoms. This results from the random and equal distribution of all atoms throughout the structure.

Further, the formation of phase diagrams and crystal structures is influenced by the thermodynamic conditions in a system, as determined by two primary equations: the Gibbs free energy (Equation (1)) and the Boltzmann entropy equation (Equation (2)) [2]. The Gibbs free energy (ΔG_mix) consolidates the enthalpy (ΔH_mix), temperature (T), and entropy (ΔS_mix) into a single parameter, serving as a key indicator for predicting spontaneous reactions and the formation of stable solutions. A reaction is likely to occur spontaneously when the Gibbs free energy is negative, achieved through negative enthalpy (typical for traditional materials) or a sufficiently large entropy term that drives the total Gibbs energy below zero [2]. The Boltzmann equation establishes a connection between the system entropy and the potential microstates. In materials with high entropy, the increases are attributed to the random alignment of atoms. Equation (2) illustrates the configurational entropy for both cation and anion positions, with R presenting the gas constant, S1 being cation sites, S2 being anion sites, and X_i and X_j representing the molar composition of each element [2]. In conventional alloys with a dominant element and several minor elements, the system’s entropy remains low. Conversely, in the creation of HEMs with equimolar compositions, the entropy term can be maximized, facilitating the formation of stable solid solutions.

In the case of an equimolar composition, the Boltzmann equation is simplified to Equation (3), where R represents the gas constant and N is the count of equimolar elements [2]. Defining a specific threshold for high entropy can vary slightly, but is generally considered to be achieved when the entropy attains a minimum value of 1.5R, necessitating the presence of five or more equimolar elements.

The determination of whether a material will attain a state of high entropy is governed by the system’s thermodynamics, as influenced by the Gibbs free energy and the Boltzmann equation. Traditional alloying techniques often fall short in meeting this criterion for high entropy. Consequently, novel synthesis techniques must be developed to enable the attainment of this elevated level of mixing.

High-entropy materials are characterized and defined by four key concepts: the high-entropy effect, lattice distortion effect, sluggish diffusion effect, and the cocktail effect [2,5,6,7]. These fundamental factors collectively contribute to shaping the distinctive features of HEMs.

The primary characteristic and foundational aspect of HEMs is the high-entropy effect. The elevation in entropy is a consequence of the heightened configurational entropy within the system, as previously mentioned. While various types of entropy exist, such as vibrational, electronic, and magnetic, it is the configurational entropy that takes precedence, exerting a dominating influence [5]. This rise in configurational entropy surpasses the enthalpy term in the Gibbs free energy equation (refer to Equation (1)), leading to a reduction in the free energy of the structure and consequently enhancing the system’s stability for HEM formation [2]. The augmented configurational entropy facilitates the creation of stable solid solutions [6].

The second phenomenon is the lattice distortion effect, stemming from the disparate sizes of atoms within the crystal structure [2,5]. In a typical alloy’s crystal arrangement, the introduction of minor atoms induces local strains, resulting in a subtle lattice distortions. In the case of HEMs, a notable degree of strain is evident in the crystal lattice due to the diverse sizes of each element that is distributed randomly throughout the structure. These lattice distortions contribute to a reduced intensity in the X-ray diffraction peaks and can be associated with the lower thermal conductivities observed in HEMs due to increased scattering. Additionally, this heightened strain can contribute to the reinforcement and fortification of HEMs [6].

The third impact is characterized by a delayed diffusion process, arising from the lattice distortions that impeded the motion of atoms within the structure [2]. Each atom within the crystal lattice finds itself encircled by diverse neighboring elements. The central atom, positioned at a specific site, experiences substantial interaction with the surrounding atoms, leading to varied bonding energies between them [7]. Consequently, this variance in bonding energies contributes to an elevation in activation energies within the HEMs, heightening the challenge of facilitating substitutional diffusion.

The phenomenon known as the cocktail effect characterizes the distinctive attributes of HEMs. In conventional alloys, supplementary elements are often introduced to enhance properties, such as corrosion resistance or hardness, typically interacting solely with the primary element. In contrast, the incorporation of additional elements in HEMs results in interactions not only with a primary element but also with multiple neighboring elements. This heightened level of interaction, stemming from the extensive mixing in the structure, gives rise to HEM properties that surpass the cumulative qualities of their individual components. The blending of multiple elements yields unforeseen properties that a single element alone cannot provide [8]. The interplay among diverse elements introduces an element of unpredictability, resulting in HEMs possessing distinctive physical properties.

The specific properties that are found in HEMs are contingent upon the synthesis process employed. Varied synthesis techniques yield different HEMs, including high-entropy alloys, oxides, carbides, etc., each exhibiting diverse characteristics such as strength, conductivity, and thermal and magnetic properties. The development towards high-entropy materials has spanned many years and has been propelled by an overall increase in chemical complexity. The complexity has increased as new elements represented the majority element and additional elements were included in minor concentrations in the compositions, increasing the overall entropy of the system.

Several methods are available to determine whether a high-entropy material has been successfully produced. Phase identification can be achieved through either X-ray diffraction (XRD) or selected area electron diffraction (SAED). Many HEMs that are formed through common HEM synthesis techniques exhibit simple crystal structures, such as rock salt, FCC, BCC, Cubic, and spinel structures. These structures can easily be identified by XRD and SAED patterns [10,11,12]. Basic crystal structures become apparent when a single-phase solution is formed, distinguishing it from a material with different phases, which is not a characteristic of an HEM [4]. However, relying solely on XRD and SAED is insufficient for confirming the successful synthesis of an HEM.

Microscopy techniques, such as scanning electron microscopy (SEM) and transmission electron microscopy (TEM), along with high-resolution TEM (HR-TEM) when nanoparticles are involved, are necessary to study the morphology of a material. In conjunction with the microscopy, energy-dispersive X-ray spectroscopy (EDX) is used to quantify the homogenous distribution of elements within a particle [4,13]. A well-formed HEM particle should exhibit homogeneous distribution of all elements at the atomic scale, which can be observed with EDX mapping techniques.

Some elemental compositions, like those involving lithium, are not easily studied using EDX techniques. The use of lithium in HEMs is common, especially in battery applications. The most precise method for determining material composition is through the use of inductively coupled plasma–optical emission spectroscopy (ICP-OES). This method helps to acquire the exact distribution of elements in the material. When lithium is included in a high-entropy material, performing ICP-OES becomes necessary, as many synthesis techniques involve elevated temperatures, and there is a concern that temperatures exceeding 800 °C during the synthesis can result in lithium evaporation [4].