Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Energy & Fuels
As a typical unconventional energy reservoir, natural gas hydrate is believed to be the most promising alternative for conventional resources in future energy patterns. The exploitation process of natural gas hydrate comprises a hydrate phase state, heat and mass transfer, and multi-phase seepage. Therefore, the study of heat transfer characteristics of gas hydrate is of great significance for an efficient exploitation of gas hydrate.
- gas hydrate
- heat transfer characteristics
- thermal conductivity
- molecular dynamic simulation
1. Introduction
Gas hydrates are compounds formed by the interaction of gas molecules and water molecules under conditions of low temperature and high pressure, resembling a crystalline lattice structure with cage-like formations [1,2]. In this structure, water molecules serve as the “host”, while gas molecules act as the “guest”, and based on the characteristics of the water molecule distribution, gas hydrates can be classified into three types: sI, sII, and sH. In natural gas hydrates, the guest molecules are low molecular weight hydrocarbon gases such as methane. They are widely found in the permafrost regions of continents and deep-sea sediment layers, but also in some ancient mountain ranges [3,4]. Under standard temperature–pressure conditions, 1 m3 of hydrate can release 0.8 m3 of water and about 164 m3 of natural gas. Currently, there is a growing global demand for natural gas resources. By 2040, the world demand for natural gas is projected to grow by a significant 44.0 percent (1.7 percent per annum), reaching a quarter of the primary energy mix (i.e., oil, natural gas, coal, nuclear, and renewables) [5]. Therefore, natural gas hydrates have attracted more and more attention worldwide due to the shortage of conventional resources and the daily increasing expectations for alternative energy [4,6]. And gas hydrates have significant applications in sustainable technologies including gas and energy storage, gas separation, and water desalination [7].
A natural gas hydrate reservoir is a multi-component complex sediment system composed of natural gas, water, hydrate, sediment, and so on. Natural gas exploitation in reservoirs involves a hydrate phase change, multi-phase seepage, heat and mass transfer, and other processes. Thus, the exploitation of natural gas hydrate is a complex and difficult process to control. As we all know, the decomposition of natural gas hydrate is a heat absorption process that can cause a decrease in the local temperature of the reservoir; if the environmental heat exchange efficiency is low, it will lead to the slowing down of hydrate decomposition near the decomposition front, the cessation of hydrate decomposition, or the secondary formation of hydrate, which seriously restricts the efficient development of natural gas hydrate [8]. Thus, the study of heat transfer characteristics of natural gas hydrate is of great significance for efficient exploitation. The current experimental methods of gas hydrate exploitation are depressurization, CO2-CH4 displacement, thermal exploitation, injection of chemical inhibitors, and the solid exploitation method. Considering the features of high yield, low environmental impact, and relatively mature technology of depressurization method, since 2002, some countries such as China, the United States, Canada, and Japan have primarily employed depressurization as the principal means of exploiting hydrate from sandy reservoirs and conducted production trials [6]. When the heat transfer is insufficient, the temperature at and around the hydrate decomposition interface will be lower than the corresponding phase equilibrium temperature, and the hydrate decomposition rate will be significantly reduced or even stopped, thus inhibiting gas hydrate decomposition. Therefore, heat transfer affects hydrate decomposition and even the efficiency of gas hydrate extraction [9]. In this method, temperature control is the key factor, so we need to understand the heat transfer characteristics of natural gas hydrates, make more use of the sensible heat of the reservoir, and enhance the heat transfer to the environment to improve the production efficiency of hydrates [10,11]. On the other hand, natural gas hydrates are stable only in a specific temperature and pressure range, elucidating the danger of climate change. For plausible changes in sea level and temperature over the next few centuries [7], the effect of rising temperatures on the gas hydrate reservoir will likely accelerate the decomposition of gas hydrates by speeding up heat exchange between the external environment and the gas hydrate reservoirs. This will reduce the rigidity of permafrost and cause geological disasters [12,13], such as sediment deformation and landslides, and seafloor slope failures on continental margins. Because of the widespread distribution of permafrost and the uncertainty of its gas hydrate content, CH4 leakage from hydrate decomposition caused by permafrost can seriously pollute the atmosphere and accelerate the global greenhouse effect [7,14].
At present, experimental tests and theoretical simulations have focused on the heat transfer process of natural gas hydrate formation and decomposition, but there are still some deviations between theoretical and experimental data, and there is no unified view on the heat transfer mechanism in the process of hydrate decomposition/formation. This is mainly because the gas hydrate reservoir is relatively complex, and the reservoir sediments are mainly porous media. Its heat transfer is affected by many factors, including pore size distribution, pore size, and heat transfer performance of the media. On the other hand, there are many heat transfer modes such as convective heat transfer, phase change heat transfer, and radiative heat transfer in hydrate formation and decomposition [15].
2. Study of Heat Transfer Characteristics of Gas Hydrate
Natural gas hydrate reservoirs contain a complex system of porous media, hydrates, water, gases, and other multi-phase and multi-component systems. The forms of heat transfer between the components include heat conduction, heat convection, and heat radiation. Therefore, the heat transfer characteristics of natural gas hydrate are affected by porous media, hydrate, water, gas, and other multi-phase structural properties, physical properties, and other factors.
2.1. Effect of Porous Media Material on Heat Transfer Characteristics of Hydrate
Li et al. [34] carried out methane hydrate decomposition experiments by using the depressurization method in porous media with three different thermal conductivities: quartz sand, white corundum, and silicon. The results showed that with the increase in ETC in porous media, the heat transfer rate increased, and the temperature rise rate of methane hydrate also increased. Wang et al. [35] studied the heat transfer effect of porous media materials by using four different porous media with different heat transfer properties: quartz sand, natural sand, corundum, and silicon carbide. The results showed that the porous medium silicon carbide with a larger ETC can improve the ETC of the whole multi-phase sediment to a greater extent, promote heat transfer in the gas production process, and eliminate the hydrate reforming and freezing caused by depressurization effectively. Yang et al. [32] measured the ETC of THF hydrate-bearing sediments using silica sands, natural sands, corundum, and silicon carbide with different ETCs. The study found that porous media with a larger ETC will improve the heat transfer performance of hydrate-bearing sediments. Subsequently, Yang et al. [36] studied the ETC of methane hydrate formation in these four porous media, obtained the same conclusion, and predicted that the ETC of porous media materials has a linear relationship with the ETC of hydrate-bearing sediments. A two-dimensional axisymmetric model developed by Zhao et al. [37] studied the effect of heat transfer on the decomposition of methane hydrate by using the heat shock method. It was found that porous media with high specific heat capacity can provide more sensible heat in a short time in the early stage of hydrate decomposition and can accelerate the rate. However, the decrease in hydrate decomposition caused by high specific heat capacity reduces the gas production rate in this process. Therefore, from the perspective of heat transfer, the reason why the decomposition rate of methane hydrate increases with the increase in ETC in porous media is that the heat of methane hydrate decomposition is provided by the sensible heat of porous media. This heat, as an in situ heat, can be immediately used for hydrate decomposition, so the decomposition rate of methane hydrate is also faster.
2.2. Effect of Porosity of Porous Media on Heat Transfer Characteristics of Hydrate
During the process of hydrate formation in porous media, fluid in the pore space of porous media contributes to heat conduction inside the pores and establishes heat transfer channels between particles for particle–fluid–particle heat transfer [38]. Priest et al. [39,40] and Best et al. [41] considered the change in heat transfer characteristics by changing the pore conditions of porous media and adjusting the distribution of hydrates. Those studies found that if the hydrate is suspended in the pore fluid, which is of the pore-filling type, there are some migration channels between the hydrate and the sediment so that the pores are filled with pore water, dissolved gas, or free gas; when the pore water is too much, it is easy to form the contact type. Tupsakhare et al. [42] studied the decomposition process of methane hydrate in porous media by using the thermal extraction method and found that free water in the pores of porous media played an important role in the process of transferring heat to hydrates far away. Dai et al. [23] emphasized the importance of non-gas phase distribution in the pore space to the thermal conductivity of unsaturated sediments. The increase in thermal conductivity may be caused by the redistribution and migration of water to neighboring contacts. When hydrate formation is associated with volume expansion, the contact area increases and water may extend into the hydrate grains and neighboring contacts, thus reducing porosity and increasing thermal conductivity. Yang et al. [32] found that the effective thermal conductivity of THF hydrate deposits was negatively correlated with porosity through experiments due to the fact that the thermal conductivity of porous media in the pore space is lower than that of hydrate crystals. Wei et al. [43] analyzed the ETC changes in hydrate-bearing sediments and THF hydrates in the South China Sea. Compaction operations reduce porosity and expel air, leading to a significant increase in the ETC of sediment-containing hydrates. The study showed that the ETC of hydrate-bearing sediments is negatively correlated with porosity. It is suggested that pore expansion may lead to a significant decrease in ETC, and pore space reconstruction may lead to heat transfer barriers. The low thermal conductivity of hydrate-bearing sediment samples in the South China Sea is attributed to the high porosity and irregular shape of the sediments. Wu et al. [44] proposed a new model for the ETC rate of gas hydrate-bearing sediments that integrates hydrate saturation and pore morphology evolution. Their findings suggest that when the intensity of pore morphological changes correlates with the pore structure and hydrate formation conditions, the ETC escalates in tandem with the increase in pore change intensity, which is contrary to the results of Yang’s [32] and Wei’s [43] study. As the hydrate pore morphology alters, given a constant water content and pore volume, the correlation between porosity and ETC is predominantly influenced by alterations in pore composition. As hydrate saturation increases, free gas is supplanted, leading to a greater hydration space occupation within the pores. Both an increase in water content within the pores and a decrease in gas content contribute to an elevated ETC in multi-phase samples. Similarly, Li et al. [30,45] evaluated the ETC of quartz sand samples containing methane hydrate formed in quartz sand with different porosities. The study found that porosity has a very obvious effect on thermal conductivity, and the ETC increases with the increase in porosity; they also found that the ETC of hydrate-containing porous media depends on the location of hydrate formation in the pore space, and the pore space also depends on the formation environment.
2.3. Effect of Particle Size of Porous Media on Heat Transfer Characteristics
Farahani et al. [46] in their study on soil thermal conductivity proposed that heat transfer in porous materials is controlled by the following particle-level mechanisms (as shown in Figure 2): (1) conduction within the particle, (2) particle–particle conduction through contact area, (3) particle–fluid–particle conduction, (4) radiation at the contact between particles, (5) conduction in pore fluids, (6) convection in pore fluids, (7) radiation media from the particle surface to the surrounding environment, and (8) radiation into the surrounding medium. Heat transfer in porous media hydrates is similar to that in soil particles, and the main factor determining the overall ETC comes from the porous media particle-level transport processes. Cortes et al. [38] studied the heat transfer characteristics in THF hydrate-bearing sediments. The particle-level heat transfer process in porous media is preferentially conducted through minerals, followed by contact conduction between particles, and finally the adjacent particle–fluid–particle contact conduction in the fluid, as well as conduction through the pore space. Jaeger et al. [47] and Nasirian et al. [48] pointed out that the contact between particles plays a key role in the heat transfer of granular media. The heat transfer between particles is proportional to the particle radius [49]. Midttomme et al. [50] posited that the rate of heat transfer in sediment increases with an increase in the particle size of the porous medium. According to the theory of heat conduction, the law is to preferentially find the path with the smallest thermal resistance. If a large contact thermal resistance exists between the porous media particles, this resistance attenuates the ETC. Li et al. [16] generated hydrates and decomposed them in sediments with four particle sizes of 14–20 mesh, 35–60 mesh, 80–120 mesh, and 400–500 mesh. From the analysis of temperature changes, it is concluded that the heat conduction rate in porous media with smaller particle sizes is also lower, which is consistent with the proportional relationship obtained by Midttomme et al. [50]. In addition, Zhan et al. [51] studied the hydrate dissociation behavior in sediments with different particle sizes, it was shown that the heat transfer of sediments increased with the increase in particle size. However, it is not accurate to judge ETC only according to the particle size. Ahn et al. [52] discovered that when the proportion of fine particles in the mixed particles is high, ETC will also increase. Wang et al. [53] employed the thermal extraction method to decompose hydrates and examined its correlation with sediment particle size. Their findings suggest that both the heat transfer rate and energy efficiency diminish as sediment particle size decreases. Larger particle sizes corresponded to enhanced permeability, potentially leading to a more expansive fluid flow sweep area, which is conducive to the heat supply of hydrate decomposition. However, in the actual hydrate reservoir, the pore and particle size of the sediment may be much larger than the artificial medium simulation used in the laboratory. The particle size distribution is shown in Table 2, and the effect of this difference on hydrate decomposition needs further study.
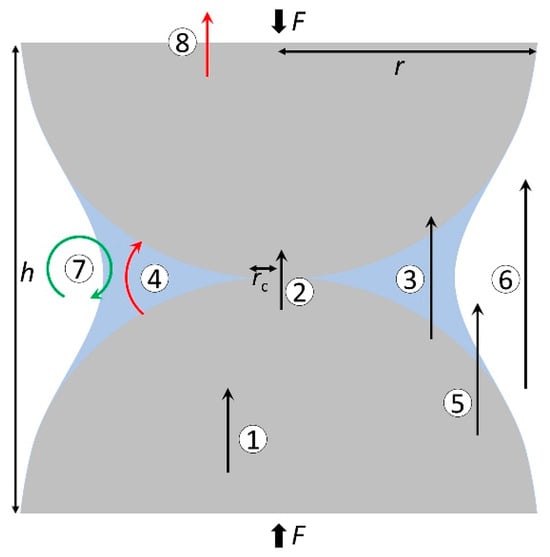
Figure 2. Heat transfer mechanisms in porous media particles ((1) conduction within particles, (2) particle–particle conduction through contact area, (3) particle–fluid–particle conduction, (4) radiation at the contact between particles, (5) conduction in pore fluids, (6) convection in pore fluids, (7) radiation media from the particle surface to the surrounding environment, and (8) radiation into the surrounding medium). The picture is taken from ref. [46]. Copyright (2021) by the American Physical Society.
Table 2. Particle size distribution of porous media.
| Category | Porous Media Materials | Normal Particle Size |
|---|---|---|
| Natural sediments | Silicon dioxide | 25–58 μm |
| Grit | 1.0–2.0 mm | |
| Montmorillonite | 0.5–25 μm | |
| Clay | 0.25–0.425 mm | |
| Artificial sediments | Silica sand | 300–450 μm |
| Activated carbon | 2.19 nm | |
| Quartz sand | 13–27 nm | |
| Glass bead | 0.105–1.397 mm | |
| Silica gel | 0.105–0.150 mm |
2.4. Effect of Hydrate Saturation and Water Saturation on Heat Transfer Characteristics
Yang et al. [32] obtained the THF hydrate ETC at 274 K by using THF and deionized water to form THF hydrates with different saturations in silica sand at different concentrations. When the porosity is constant, the lower the THF hydrate saturation, the higher the water saturation in the pores, and the higher the ETC, which helps to improve the ETC of hydrates. Dai et al. [23] measured the thermal conductivity of samples with different hydrate saturations and found that gas saturation was the dominant saturation component in unsaturated samples. The ETC of unsaturated hydrate-bearing sediments is largely affected by the volume fraction, pore size distribution of the hydrate, and the aqueous phase. When the porosity remains constant, the lower the saturation of the THF hydrate and the higher the water saturation in the pores, resulting in a higher ETC [32]. Dai et al. [23] studied the change in ETC during the formation of methane hydrate and found that ETC increased after hydrate formation when the hydrate saturation was less than 20%, while ETC decreased after hydrate formation when the hydrate saturation was 30~40%. The analysis showed that the increase was due to the increase in contact area caused by volume expansion during hydrate formation, while the decrease was due to the expansion of the sedimentary skeleton or contact separation of particles during hydrate formation, and the contact mode may change from particle–particle to particle–hydrate–particle or even particle–gas. Wang et al. [35] interpreted this relationship as follows: with increasing hydrate saturation, free gas is replaced and more pore space is occupied by the hydrate; the ETC of the hydrate-bearing sediments significantly changes with increasing hydrate volume in pore space. The effect of water saturation is due to the fact that water acts as a relatively large heat transfer bridge to promote heat transfer between particles [54]. Wei et al. [55] attributed this relationship to the correlation of cementation and heat transfer between particles in porous media and the easy phase transition property of the low-saturation sample skeleton. Subsequently, they studied the effect of hydrate distribution on ETC in the process of hydrate formation in quartz sand. With the increase in water saturation, the water distribution gradually expanded, and some heat transfer paths changed from ‘particle–water–particle’ to ‘particle–particle’, making ETC increase [56].
In view of the effect of water/hydrate saturation on ETC in different actual situations, some research has established models based on theory to analyze the causes of the influence. Sun et al. [25] established a model for the ETC of hydrate-bearing sediments. After simulation, it was concluded that the relationship between ETC and methane hydrate saturation is saturated > supersaturated > unsaturated. Therefore, there is a critical saturation of hydrate; when hydrate decomposition makes most of the cementation between porous media disappear, the cementation rate decreases rapidly, which is the critical saturation. Li et al. [57] pointed out that when the saturation of the hydrate decreases to the critical hydration saturation, the decomposition of the hydrate leads to a weakening of cementation between porous media and the heat transfer rate will decrease rapidly. Wu et al. [44] established a model for the ETC of natural gas-containing hydrate sediments. It was found that under the critical saturation of the hydrate, when the pore morphology of the hydrate changed from pore filling to particle coating, ETC decreased significantly but was not obvious. However, in an excess gas environment, ETC was significantly enhanced at critical hydrate saturation. Therefore, the ETC of hydrate-bearing sediments is very sensitive to hydrate saturation near the critical hydrate saturation threshold.
A gas hydrate reservoir is a multi-component complex sediment system, and the thermal conductivity of these components is different by one order of magnitude [38,58]. Therefore, the ETC of the gas hydrate reservoir is more complex, which is not only related to porous media material, pore structure, and particle size distribution, but also related to water content, hydrate saturation, and distribution. In a gas-saturated environment, ETC is mainly affected by hydrate saturation because the thermal conductivity of the hydrate is higher than that of gas. Whereas, in a water-saturated environment, ETC is mainly affected by water saturation [59].
2.5. Effect of the Hydrate Dissociation Process on Heat Transfer
Hydrate decomposition is a solid–gas–liquid phase transition process. In their study on propane hydrate decomposition, Kamath et al. [60] divided the process of hydrate decomposition into three stages, solid stage, liquid stage, and gas stage, emphasized the influence of the phase transition process on heat transfer, and pointed out that the bubble generated by the rapid release of gas from hydrate decomposition dominates the heat transfer process. Later, Kamath et al. [61] further proposed that hydrate decomposition is in turn limited by the heat transfer process in their study on methane hydrate decomposition. The water produced by hydrate decomposition continuously forms a thin liquid film on the surface of the undecomposed hydrate, thereby generating resistance to heat transfer. Zhao et al. [62] divided the decomposition region into three regions, the decomposed region, the decomposing region, and the hydrate region, when analyzing hydrate decomposition in porous media. The heat transfer path between regions is mainly transferred from the decomposing zone containing the hydrate to the decomposing zone containing gas and water. Their study found that the convection caused by the gas produced by the decomposition reduced the ETC and heat capacity of the hydrate. This confirms the conclusion previously mentioned by Pooladi-Darvish et al. [63] that gas convection leads to a decrease in heat capacity and gas production rate. Kou et al. [64] refined the heat transfer effect of the hydrate dissociation stage (as shown in Figure 3): stage 1 is the depressurization stage, where the decomposition heat source is mainly provided by the heat conduction from the environment; stage 2 is the constant pressure stage, where the heat source is mainly provided by the sensible heat, and the partially decomposed hydrate structure provides a new dissipative channel for heat transfer. When the sensible heat of hydrate-bearing sediments is consumed, the heat conduction from the environment becomes the main driving force of decomposition. Zhang et al. [65] established a hydrate dynamic decomposition model to simulate the decomposition process of hydrate particles in flowing water. When hydrate particles move in water, the heat transfer mode is heat conduction inside the particles and heat convection between hydrate particles and water. In the early stages of hydrate particle decomposition, the heat transfer on the surface of hydrate particles is dominant. When the surface temperature of hydrate particles gradually stabilizes, the internal heat transfer of the hydrate plays an important role, and the heat transfer rate of hydrate particles cannot be ignored. When considering the heat transfer of hydrate decomposition, Hao et al. [66] proposed that the two heat transfer modes of heat conduction and heat convection should be considered at the same time, as heat convection is the key factor of natural gas hydrate decomposition. Different from the influence of gas or water disturbance on heat transfer in the process of water and matter decomposition mentioned above, some scholars have analyzed the influence of hydrate heat transfer through the change in hydrate structure in the process of hydrate decomposition. In the work of Kanda et al. [67], they used a high-speed phase-shifting interferometer to observe the interfacial heat transfer phenomenon of methane hydrate and calculated the apparent density difference distribution near the interface. Wei et al. [43] used this idea to observe the changes in hydrate density and density distribution during the phase transition of hydrate decomposition by comparing the ETC changes in the THF hydrate during the decomposition process. It was concluded that the hydrate decomposition process destroyed the heat transfer path in the original hydrate system, which reduced the interface thermal resistance, in turn leading to an increase in the ETC of THF hydrate. He et al. [59] proposed an explanation for the change in the specific heat transfer path in the decomposition stage of methane hydrate. In the early stages of hydrate decomposition, the ETC increased due to the expansion of the water distribution range. In the later stages, the heat transfer path changed from ‘particle–water–particle’ to ‘particle–gas–particle’, and the contact mass between particles decreased, resulting in a downward trend of ETC.
Figure 3. Temperature changes at different temperature measurement points in hydrate decomposition process. The picture is taken from ref. [64]. (Point A is the turning point where the temperature trend of the system changes from decreasing to steady.) Copyright (2019) with permission from Elsevier.
2.6. Effect of Environmental Heat Conduction on Hydrate Dissociation Process
Li et al. [68] observed the evolution of the hydrate temperature gradient and the increase in temperature in the decomposition area of the hydrate boundary area in the experimental and simulation study of the hydrate depressurization decomposition process in sediments. In their study, the energy transferred from the surrounding environment was used as the latent heat in the process of hydrate decomposition equilibrium, and then, it was concluded that the heat transfer around the reservoir has an effect on the depressurization decomposition process. Li et al. [69] further analyzed the heat transfer characteristics of depressurized decomposition of methane hydrate near the freezing point and found that heat conduction from the environment is mainly the sensible heat of the reservoir, the boundary conduction heat, and the transition latent heat of ice. Wan et al. [70] found that under thermal stimulation, heat conduction plays a role in the early stages of hydrate decomposition, while hydrate decomposition mainly transfers heat from the environment under depressurization conditions. Oyama et al. [71] pointed out that the dissociation process of the hydrate is dominated by the heat transfer process around the hydrate core by analyzing the temperature distribution changes in the core center and the wall surface during the hydrate dissociation process. Heat transfer affects the temperature distribution in the hydrate, thereby controlling the hydrate decomposition process. Chen et al. [72] found that the combination of pressure and heat transfer in the hydrate decomposition process is the main driving force. In the early stages of decomposition, the driving force comes from the pressure and sensible heat of the sediment hydrate. When the temperature decreases to the phase equilibrium temperature, the decomposition enters the later stage. The driving force of this process comes from the pressure of the surrounding environment and the external heat transfer. In the process of decomposition, free water will migrate to the upper part of the system and affect the heat transfer. Robert et al. [73] and Mehran et al. [74] used numerical simulation to study the heat transfer process of hydrate depressurization decomposition with phase changes in porous media and proved that heat transfer and temperature gradient distribution inside the reservoir are the main driving forces of the depressurization decomposition process. It can be seen that heat transfer, as the basic control mechanism of the hydrate decomposition process, directly affects and controls the hydrate decomposition rate and decomposition efficiency, and has a crucial impact on the efficiency of natural gas hydrate decomposition.
This entry is adapted from the peer-reviewed paper 10.3390/en17030717
This entry is offline, you can click here to edit this entry!
