Liquid Crystal Lenses | Encyclopedia MDPI

Liquid Crystal Lenses: History

View Latest Version

Please note this is an old version of this entry, which may differ significantly from the current revision.

Subjects: Optics

Contributor:

José M. Otón

Javier Pereiro-García

Liquid crystal (LC) lenses may be used by themselves or as a supplement of glass lenses, e.g., to tune up the power of the glass lens within a certain range, with functionality equivalent to commercial progressive lenses, but with improved performance since the power of the whole lens is modified by a sensor providing autofocus, as in digital cameras.

liquid crystal (LC)

1. Graded Index Lenses

Let us design a flat–convex convergent thin lens (paraxial approximation). A fixed lens can be made with a flat–convex glass whose thickness is determined by the desired power in diopters (the inverse of focal length). A tunable lens can be made with a flat liquid crystal cell (graded index or GRIN lens, Figure 1), achieving a switching profile across the cell that mimics the glass profile in terms of the optical path,

n \cdot L

, the refractive index, and the physical path.

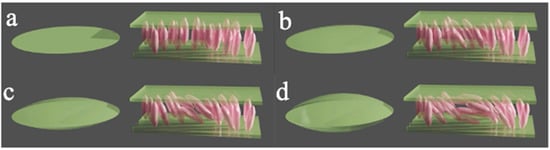
Figure 1. A glass lens and a liquid crystal GRIN lens are optically equivalent. The LC molecules are partially switched, more tilted at the center and less tilted at the edges. This generates a refractive index gradient that modifies the optical path of the light impinging from the bottom plate. The sequence (a–d) shows lenses with increasing power, i.e., thicker glass lenses and more tilted LC lenses.

A lens is formed when the optical path along the lens radius decreases quadratically with distance from the center. Both the refractive index (birefringence,

Δ n

) or length (lens thickness,

Δ L

) can be varied to achieve optical path variation. Glass lenses vary the glass thickness, while liquid crystal lenses vary the refractive index:

Glass : n \cdot Δ L Liquid crystal : Δ n \cdot L

Theoretically, both mechanisms are equivalent; however, this is not the case in working conditions. Assuming to manufacture a 1 cm flat–convex lens with a power

P = 5

diopters (i.e., a focal length F = 20 cm). The curvature R₂ of the glass lens can be calculated to within a thin-lens approximation using the lensmaker formula [26]:

P = \frac{n_{g l a s s} - n_{o u t}}{n_{o u t}} (\frac{1}{R_{1}} - \frac{1}{R_{2}})

Assuming

n_{g l a s s} = 1.5

and

n_{o u t} = 1.0

(air), the curvature

R_{2} = 10

cm. If the lens has a diameter of 1 cm, then the thickness of the lens (strictly, the difference between the thickness at the lens center and its borders) is 0.125 mm, which can be easily fabricated.

2. Designing Liquid Crystal Lenses

In liquid crystal cells, the situation is different. A quadratic index profile is required, as above; moreover, the profile must be variable so that the lens can be tunable. Several solutions have been proposed to achieve this quadratic profile with adaptive focus:

Zonal or pixelated lenses generate the quadratic index profile through independent electrodes. SLMs can be used to make such lenses; however, it is usual to employ pixels shaped as concentric rings [27].
Modal lenses can produce smooth profiles without pixelization, with just one continuous electrode or a few of them at most. The electric field distribution—hence the index profile—is achieved by employing high-resistivity electrodes, usually between 100’s $k Ω /$ □ and some $M Ω /$ □. High-resistivity electrodes can be made of several materials, such as poly(3,4-ethylenedioxythiophene) polystyrene sulfonate (PEDOT-PSS) [28] or ultrathin indium–tin oxide (ITO) [29].
The high-resistivity electrode behaves as a transmission line [30], and the profile can be modified by varying the voltage amplitude and the frequency, therefore making it possible to create radial voltage gradients that follow up the required quadratic index profiles for lenses or other profiles for different optical elements, e.g., axicons. Modal control has also been proposed in the Fresnel lens [31], which will be commented on below.
Some fancy electrode designs have been proposed as well to contribute to the electric field distribution, e.g., serpentine electrodes [32], spiral electrodes [33], or rectangular aperture lenses [34].
A rather different approach is given by Pancharatnam–Berry phase devices (PPD, [35]), specifically Pancharatnam–Berry lenses. PPDs are elements in which electromagnetic waves undergo continuous phase changes due to a continuous change in the material through which they are passing. Typically, liquid crystal PPDs work by smooth variations of the alignment directions on both the confining surfaces of a $λ / 2$ retardation liquid crystal cell, i.e., introducing a fixed linear retardation with variable azimuthal angle.

Such a PPD inverts the handedness of incident circularly polarized light and introduces a relative phase delay depending on the local alignment direction of the

λ / 2

waveplate, as will be discussed below. These devices and lenses have a wide range of applications with a spatial phase variation pitch beyond anything achievable in conventional SLMs or ITO-based devices [36,37].

However, unless special effort is invested, the devices will have opposite behavior for the two-handedness of circularly polarized light, which makes them “unstackable” and typically only provide an ON–OFF switching behavior optimized for a single wavelength. Thus, the main drawbacks of PPDs are their deficient tunability and their strong dependence on the wavelength of impinging light [38].

Nonetheless, the lens power achieved by regular materials (except PPDs) is quite modest. The quadratic index

n_{r}

at a given distance

r

from the center is defined as

n_{r} = \frac{n_{e f f} - n_{o}}{r_{0}^{2}} \cdot r^{2} + n_{o}

where

n_{e f f}

is the refractive index at the lens center

n_{e f f} = \frac{n_{e} n_{o}}{\sqrt{(n_{o}^{2} \sin^{2} θ + n_{e}^{2} \cos^{2} θ)}}

where

θ

is the angle between the LC optic axis and the direction of light propagation [39].

n_{e f f}

can reach the extraordinary index

n_{e}

;

n_{o}

is the ordinary index at the cell edges, and

r_{0}

is the cell radius. It can be easily shown by geometrical considerations [40] that the power

P_{L C}

of a thin LC lens with quadratic index profile is

P_{L C} = \frac{2 \cdot Δ n_{e f f} \cdot L}{r_{0}^{2}} = \frac{1}{f}

where

L

is the LC cell thickness,

Δ n_{e f f} = n_{e f f} - n_{o}

, and

f

is the focal distance. This dependence on the square of the radius is critical for LC lens performance. A typical LC has a birefringence (BR) around

Δ n = n_{e} - n_{o} \approx 0.2

. Using the same 1 cm lens above in an LC cell of standard thickness (e.g., 8 µm) and assuming the maximum BR is achieved, the power yielded by the LC lens is as low as 0.13 diopters.

Clearly, the problem arises from the low phase delay

δ

induced between the center and the edges of the LC lens. According to the delay formula

δ = \frac{2 π}{λ} \cdot Δ n_{e f f} \cdot L

Assuming

Δ n_{e f f}

reaches

Δ n

, the induced delay is 5.82π in the green region (550 nm) and 5.06π in the red region (633 nm). This is more than enough for applications such as displays or phase gratings but too small for lenses or beam steerers.

3. Increasing Liquid Crystal Lens Power

Several solutions have been proposed to overcome this problem [41]:

Use of high-birefringence LCs [42]. This can be helpful, but it is not a solution by itself. At present, high-BR mixtures are in the range of 0.4–0.5, which would double or triple the lens power at most.
Increase of the cell thickness. LC cell thicknesses above 100 µm driven by ultrasounds have been proposed [43]. For electrically driven cells, however, thickness is severely restricted—usually to 20–30 µm—by response-time degradation and poor material orientation in thick cells. Again, alternative solutions, including dual-frequency nematics [44] and polymerization [45], have been proposed so that the spatial orientation of LC molecules is kept and the response time is improved.
Decrease of the cell radius. This would alleviate the strong dependence $r^{2}$ that thwarts the lens power. A $P = 5$ diopters lens of 1 cm diameter, like the above glass lens, would require an LC thickness of 314 µm, which would be impossible to control or orient with standard fabrication procedures. (Unsurprisingly, this is the thickness difference required for the glass lens, where its refractive index is 1.2 rather than 1.5, i.e., $Δ n = 0.2$ ). If the LC lens diameter is set to 2 mm, then the required LC thickness is 12.5 µm, a perfectly feasible value. Many groups work on LC microlens arrays [46,47] to take advantage of small diameters while keeping reasonable apertures.
Creation of Fresnel lenses. Fresnel geometry provides the most powerful solution, capable of producing high-power, high-aperture lenses [48] with outstanding fill factor and excellent time response.

This entry is adapted from the peer-reviewed paper 10.3390/cryst14010016

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.