Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Parallel computing, a significant portion of the problems faced by serial computing are gradually becoming obsolete. In both academic and industrial settings, the technique of parallel computing is often employed by researchers and industry practitioners alike to hasten the simulation-based optimisation processes.
- simulation
- computational cost
- optimisation
- composite
- liquid composite moulding
1. Introduction
Currently, large-scale composite manufacturing is commonly achieved via liquid composite moulding processes [1,2,3,4]. The utilisation of numerical process simulation has greatly facilitated the challenging task of LCM process optimisation, providing ease of solution evaluation at a significantly reduced cost compared to complete reliance on physical prototyping. Nevertheless, the computational cost of performing such composite moulding simulations is still considerably expensive at present, given its complexity [5,6,7]. As a consequence, the overall computational cost of simulation-based optimisation can be enormous, as each solution evaluation is essentially a numerical simulation run that typically requires a long computing time. In fact, within the setting of simulation-based optimisation, the cost of computing the process simulation accounts for a major portion of the total optimisation cost associated. Full-scale numerical simulation of the mould-filling process can become progressively cost-prohibitive to compute as the number of optimisation iterations required increases. Moreover, as more sophisticated and accurate multi-scale coupled textile-flow models are progressively being developed, the cost of simulation will further increase in the future, likely by a significant margin compared to contemporary meso-scale Darcy’s-Law-based flow models [6,8,9]. Therefore, the high cost of process simulation, in terms of both the computational power and computation time required, needs to be addressed promptly as the key bottleneck to the application of simulation-based optimisation. Principally, the high cost of simulation-based optimisation can be effectively addressed by either: (i) reducing the total number of solution evaluations required during the optimisation process, and/or, (ii) reducing the computational cost of the process simulation [7,10,11,12].
As highlighted in [6,8], the felicitous selection of optimisation algorithms with respect to the problem context (i.e., mould-filling scenario) can greatly reduce the number of solution evaluations required during the optimisation process. Aside from the appropriate selection of optimisation algorithms, how one can effectively utilise problem-specific knowledge and information to streamline the optimisation framework also receives massive attention in the research community [13]. The inclusion and exploitation of known problem structures and characteristics, process constraints, and insights of the mould-filling process during algorithm development and implementation can significantly lessen the resultant optimisation cost.
2. Parallel Computing
In the recent past, computer algorithms have conventionally been developed for serial computing [14,15,16,17]. Consequently, when solving a problem, only a single task (or instruction) is executed at any moment in time. As a result, there is an inefficient utilisation of the hardware resources available, where only a part of the potential computing capability is employed at any particular instance. Nowadays, these superannuated approaches to algorithm design are being progressively phased out as developments in parallel hardware architecture progress steadily [14,17,18]. Thanks to the rapid advancements in the field of parallel computing, a significant portion of the problems faced by serial computing are gradually becoming obsolete. In both academic and industrial settings, the technique of parallel computing is often employed by researchers and industry practitioners alike to hasten the simulation-based optimisation processes [7,10,19,20]. The streamlining of the simulation-based optimisation process via parallel computing for LCM process optimisation is no exception [7,20,21]. Parallel computing can be understood as the act of breaking down a larger, complex problem into numerous smaller, independent sub-tasks and computing them simultaneously across multiple processing units. The individual outputs of these parallel sub-tasks can then be remerged, upon their completion, back into the original problem framework for completion or further analysis. The schematic framework of parallel computing is depicted in Figure 1.
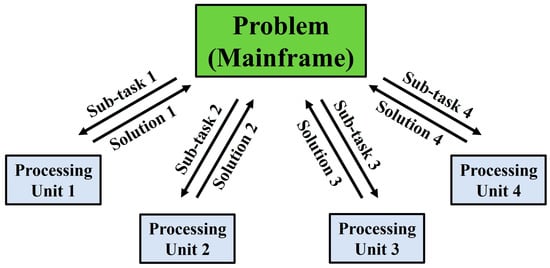
Figure 1. The schematic framework of the application of parallel computing to solve a problem.
Parallel computing offers several advantages over conventional serial computing. The apportion of a complex problem into multiple independent sub-tasks allows the total computational load to be distributed (either evenly or unevenly) across all available processing units to be computed in parallel simultaneously. Therefore, the undesirable wastage of unutilised or underutilised (idle) computing power can be minimised, which is particularly critical in the modern era where multi-core processors are progressively becoming the norm. In addition to the effective distribution and utilisation of computing power, parallel computing also enables the effective employment of non-local resources (e.g., on a wide area network or over the internet) when the local resources are inadequate. Larger problems, too large to fit into a single machine’s memory, can alternatively be solved via parallel computing, thus alleviating hardware constraints while introducing a massive scale-up of computational potential compared to that of local serial computing.
Most importantly, parallel computing allows parallelisable algorithms and applications to be computed within a shorter wall-clock time than serial computing (i.e., faster algorithm execution). While the total computational load remains unchanged, independent computing tasks can be distributed across multiple processors or computing machines, drastically compressing the computing time required from start to finish [15,17,21,22]. The computational time saving is commonly quantified by the speedup, which is defined as the proportion of the cost of solving a parallelisable problem/algorithm via a single processing unit versus that of solving it parallelly across multiple processing units. In the context of minimising the cost of simulation-based optimisation problems, studies across the literature have reported appealing cost reductions ranging around the range of 65% to as high as 92% [8,22,23,24]. The reduction in computing time attained via parallel computing effectively accelerates the respective project timeline and compresses the corresponding time to market, giving the users a competitive edge over their competitors. Last, but not least, parallel computing helps facilitate real-time updating and monitoring of the process progression while the upcoming computations are performing in the background, bringing concurrency and flexibility to its users [7,14,17,25].
There are many strategies for implementing parallel computing in simulation-based optimisation settings, with their selection dependent on the problem at hand. It is worth noting that the implementation of parallel computing is, to a certain extent, restricted by the (parallel) hardware architectures alongside that of the algorithm. With respect to the state-of-the-art technological advancements to date, parallel computing can be executed on multitudes of parallel architecture hierarchies, ranging from a single computer equipped with multiple processing units (CPUs, GPUs, cores) to cloud computing and computer clusters (or grids) that host multiple network-connected stand-alone computers [10,14,18,22]. Currently, there are four broad types of parallelism achievable in parallel computing, namely: bit-level parallelism, instruction-level parallelism, task parallelism, and data-level parallelism [14,17,18]. The topic of interest here, which is the cost reduction of simulation-based optimisation via parallel computing, mainly pertains to task parallelism and data-level parallelism. When performing the simulation-based optimisation, optimisation algorithms that can execute the search process without requiring knowledge of prior solution evaluations can be parallelised for parallel computing. This generally pertains to algorithms that attempt to solve the optimisation problem by brute force, with some examples including the exhaustive search and unguided random search. For this kind of algorithm, the adoption of parallel computing will potentially lead to a maximum theoretical speedup 𝑆𝑇𝐻𝐸𝑂𝑅𝐸𝑇𝐼𝐶𝐴𝐿 proportionate to N:

where N can be either:
- (i)
-
the number of processing units, or
- (ii)
-
the size of the problem, depending on the hardware’s parallel architecture. Note, only a minor proportion of all contemporary algorithms can be decomposed into completely independent pieces, enabling the theoretical linear speedup.
Besides that, the inherent parallelism of population-based algorithms (i.e., evolutionary algorithms) can also be exploited. This is so as population-based algorithms typically consider or evaluate multiple candidate solutions collectively prior to each impending search phase, as depicted in Figure 2. Effective parallelisation is thus possible as the outputs of the solution evaluation of each candidate solution are distinct from each other, allowing them to be computed independently. Some notable examples include the genetic algorithm, ant colony optimisation, and particle swarm optimisation.
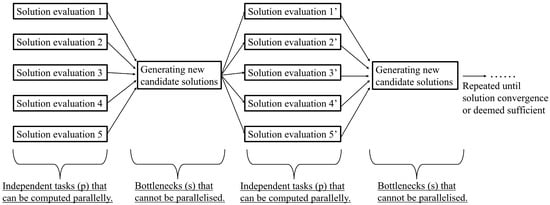
Figure 2. The generic search flow diagram of population-based optimisation algorithms.
By performing the independent solution evaluations simultaneously, the search process of the population-based optimisation algorithms can be expedited significantly. Do note, the maximum performance improvement achievable is limited by the fraction of parallelisable components within the population-based optimisation algorithms. The theoretical speedup 𝑆𝑇𝐻𝐸𝑂𝑅𝐸𝑇𝐼𝐶𝐴𝐿 for the population-based algorithms by parallel computing can be expressed by the Amdahl’s law [14,15,17,22], as:

where P is the fraction of the independent tasks within the algorithm that can be executed parallelly (e.g., evaluating the individuals within each generation of GA) and N is the number of processing units utilised.
Parallel computing can also be adopted to minimise the computational cost of the statistical modelling and characterisation for LCM processes via the Monte Carlo simulation approach [8,14,22]. These statistical analyses are critical to combat the issues of process randomness and lack of process repeatability within the LCM processes [8,26]. Parallel computing allows the user to perform the parallel computation of stochastic simulations for statistical modelling purposes and to perform parallel replications of a stochastic simulation for statistical characterisation purposes. Minimising the computational cost of these stochastic simulations will aid in securing the process robustness of the mould-filling stage [7,8,27]. Additionally, parallel computing can also be extremely valuable for the development and training of metamodels as the metamodel training data required are generally independent of one another, allowing parallelism [7,8,14].
While there are many levels of parallelism attainable, not every optimisation algorithm can exploit the merits of parallel computing in the setting of simulation-based optimisation. The adoption of certain algorithm structures, which is often dictated by the nature of the problem itself, may prohibit the simultaneous execution of computing tasks and prevent effective parallelisation [8,14,17,24]. Moreover, the issue of flow dependency is also pertinent to the adoption of parallel computing in simulation-based optimisation. Flow dependency, also commonly known as read-after-write (RAW), refers to the scenario where the execution of a task is dependent on the output of its preceding task [14,15,17,24]. As such, parallel computing is practically ineffectual for single-solution serial optimisation algorithms that: (i) evaluate only a single candidate solution during each evaluation iteration; and (ii) require knowledge of prior solution evaluation(s) to guide the following search phase (i.e., the exploration/search mechanism). For this type of algorithm, as each search phase is dependent on the result of its prior solution evaluation(s), the upcoming search tasks are forced to remain on hold until the prior solution evaluation is completed, preventing the effective distribution of computational workload. The generic search flow diagram of single-solution serial algorithms is depicted in Figure 3.

Figure 3. The generic search flow diagram of single-solution serial algorithms.
In summary, while the adoption of parallel computing has great potential in the application of simulation-based optimisation, its efficacy and applicability are highly dependent on the degree of achievable parallelism imposed by the algorithm’s framework and its flow dependencies [8,14,17,21]. Besides that, the application of parallel computing requires the development and execution of additional auxiliary algorithms to parallelise the existing optimisation framework (e.g., for task partitioning, task scheduling, task synchronisation, etc.) [14,17,19,22]. Lastly, the framework of parallel computing can be challenging to construct and implement. The complex operations of data transfer, memory organisation, communication, and synchronisation between multiple (locally or non-locally) independent processing units may require a significant effort to maintain smoothly [14,15,16,17]. In particular, issues arising from network latency and the non-homogeneity in computational power across the independent processing units can greatly complicate the vital tasks of communication and synchronisation during parallel computing. The overhead cost of these control operations can also be a deterrent to the adoption of parallel computing, as these fundamental operations can be computationally demanding to execute as well [14,16,17,19]. A delicate trade-off between the additional computational cost required versus the computational time saved is thus essential for the effective application of parallel computing in simulation-based optimisation settings.
This entry is adapted from the peer-reviewed paper 10.3390/ma16247580
This entry is offline, you can click here to edit this entry!
