Advanced Supercritical CO2 Thermodynamic Power Cycles: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Xinyu Zhang
,
Yunting Ge

CO2 is a natural, non-toxic and non-flammable working fluid that possesses excellent thermophysical properties, including higher density, latent heat, specific heat, thermal conductivity and volumetric cooling capacity, along with lower viscosity.

  • CO2 working fluid
  • supercritical power cycles
  • renewable energy
  • advanced power generation systems

1. Introduction

Global energy demand is on the rise in numerous countries as the population increases and the economy grows. One of the primary and representative facts of economic growth in all countries worldwide is the increased electricity demand and generation. From 2019 to 2022, total primary energy consumption experienced a 3% increase, while the proportion of fossil fuel consumption in relation to primary energy consumption remained high at approximately 82% [1]. Growing energy consumption makes it a significant challenge to transition our energy sources and supplies away from fossil fuels and move towards low-carbon ones. Extensive fossil fuel consumption has caused environmental issues such as global warming, ozone depletion and atmospheric pollution. Therefore, it is critically important to achieve energy conversion efficiency improvement and increase renewable energy utilization and thus diminish the reliance on fossil fuels.
A decentralized and localized power generation system is an effective option to reduce energy consumption since energy loss from long-distance transmission or transportation can be avoided. Steam Rankine and gas turbine cycles have been significantly involved in large-scale power plants for electricity generation. The steam Rankine cycle can, however, achieve relatively higher energy conversion efficiency at lower turbine inlet temperature, considering the fact that the working fluid is pumped at a liquid state before being heated by a steam boiler. This is significant because liquid water is essentially incompressible, which can reduce the work required for pumping compared to compressing a gas by a compressor. According to the theory of the Carnot cycle for a heat engine, the higher the temperature at which heat is supplied and the lower the temperature at which heat is rejected, the greater efficient the cycle will be. It reveals the importance of a power cycle operating at a higher heat supply temperature whenever possible to maximize its thermal efficiency. The gas turbine cycle, also known as the Brayton Cycle, utilizes air as a working fluid at a higher turbine inlet temperature. However, in the Brayton Cycle, the compression process consumes more work compared to the steam Rankine cycle since air is compressible. This leads to lower efficiency for the gas turbine cycle. On the other hand, over the last decades, as a mature energy conversion technology, the organic Rankine cycle (ORC) has been generally used in small-scale power generation. Industrial waste heat, biomass combustion, solar energy and geothermal heat can be utilized as heat sources for ORCs [2][3]. The ORC is superior to the traditional steam Rankine cycle in terms of performance when employing a low-temperature heat source. However, the selection of a working fluid for an ORC is a challenge due to the fact that some organic compounds have high global warming potentials (GWPs). Therefore, the investigation of alternative working fluids in applicable power generation cycles attracted more attention [4][5]. CO2 is a natural, non-toxic, non-flammable, abundant and zero ozone depletion potential (ODP) working fluid, making it a noteworthy competitive candidate to be utilized in a power generation system [6]. According to its low critical point, the CO2 power cycle can easily extend to the supercritical region and turn it into a transcritical or supercritical CO2 power cycle. The supercritical CO2 (S-CO2) power cycle was originally proposed as a format of partial condensation Brayton cycle by Sulzer [7] in 1940. A simple recuperated supercritical Brayton cycle was propositioned by Feher [8] in 1967, and thereafter, Angelino [9][10][11] conducted a thorough study of CO2 power cycles. The S-CO2 Brayton cycle integrates the strengths of the steam Rankine and the gas turbine cycles by compressing the working fluid in the incompressible region and achieving higher thermal efficiency at higher turbine inlet temperatures.
S-CO2 power cycles equipped with advantages of simplicity, compactness, sustainability and cost-effectiveness have therefore been significantly researched for various applications, including fossil fuel power plants, nuclear power plants, and integrations with renewable energies. The existing power cycles, such as Rankine and gas turbine cycles, face the challenges of working fluid selections and less cycle thermal efficiencies. Driven by the better thermal performance of energy conversion systems, CO2 has attracted more attention to be utilized as an alternative working fluid. Another reason is the lower critical temperature at 31 °C which enables CO2 working fluid and its associated system to be applicable in a variety range of heat sources. A power cycle with CO2 working fluid could be classified as either a direct or indirect Brayton cycle. The semi-closed direct-fire oxyfuel Brayton cycle was suitable for fossil fuel power generation systems, while the indirect Brayton cycle was adapted for applications involving nuclear and renewable energy sources [12]. There have been many studies investigating the applications of direct S-CO2 cycles. A design was conceptualized by Le Moullec [13] for a coal-fired power plant with 90% post-combustion CO2 capture. It showed that the cost of electricity and the cost of CO2 reduction could be reduced by 15% and 45%, respectively. Mecheri and Le Moullec [14] conducted additional simulations on S-CO2 coal-fired power plants, concluding that by combining a coal-fired power plant with a double reheated single recompression Brayton cycle, a net thermal efficiency of 47.8% could be attained. This efficiency was significantly higher than that of traditional coal-fired power plants. Xu et al. [15] reached a similar conclusion, stating that the net power generation efficiency of a triple-compression S-CO2 cycle could attain 49.01%, compared to 48.12% achieved by the water–steam Rankine cycle. In addition, although the fabrication cost could be increased, the levelized cost of electricity achieved a reduction of 1.32% compared to the water–steam Rankine cycle. Optimizing the recuperator in the system is crucial to reducing the total cost of the entire S-CO2 cycle. To further enhance the performance of the S-CO2 coal-fired power plant, employing a partial flow mode in the S-CO2 boiler was demonstrated to effectively decrease pressure drop, thereby increasing the system’s thermal efficiency [16]. As for the indirect Brayton cycle, significant attention was paid to the S-CO2 applications in nuclear reactors, as they could offer higher turbine inlet temperatures, potentially enhancing the system’s thermal efficiency. Various countries have undertaken efforts to develop Generation IV nuclear reactors, given that these reactors operate in the temperature range of 500 °C to 900 °C, compared to water-cooled reactors with operating temperatures at around 300 °C [17]. Dostal [18] conducted an in-depth analysis of the S-CO2 cycle for nuclear reactors. The study revealed that the S-CO2 cycle exhibited competitive system efficiency compared to the helium Brayton cycle at the same operating condition. Additionally, it was concluded that the S-CO2 power cycle was apt for all nuclear reactors with a core CO2 gas heater outlet temperature exceeding 500 °C. Moisseytsev and Sienicki [19] investigated several alternative cycle layouts for S-CO2 Brayton cycles coupled to the sodium-cooled fast reactor (SFR). It was found that no advantages could be gained from utilizing a double recompression cycle, incorporating intercooling between the main compressor stages or applying reheating between the high-pressure and low-pressure turbine cycles. However, optimizing the minimum cycle temperature down to 20 °C could lead to improvement in cycle efficiency. Wright et al. [20] demonstrated that integrating light water reactors (LWRs) with an S-CO2 cycle could potentially improve the LWR power cycle efficiency and save capital costs. In order to further evaluate the benefits of coupling an S-CO2 Brayton cycle with a small- and medium-sized water-cooled nuclear reactor (SWR), the effects of different operating conditions on system performance were studied by Yoon et al. [21]. The results revealed that even though the S-CO2 cycle was previously recognized for having superior efficiency in high operating temperature regions, the efficiency of S-CO2 with SMR cycle still demonstrated competitive efficiency to the existing steam-Rankine cycle with SMRs (around 30%) at the optimum pressure ratio. Additionally, a conclusion aligning with Wright [20] was reached that by combining the S-CO2 cycle with SWR, capital costs could also be reduced. In 2021, about 440 nuclear power reactors were in operation in 32 countries worldwide with a total generated power of 2653 TWh, which took about 10% of the global electricity supply [22].

2. Superior Thermal–Physical Properties of CO2

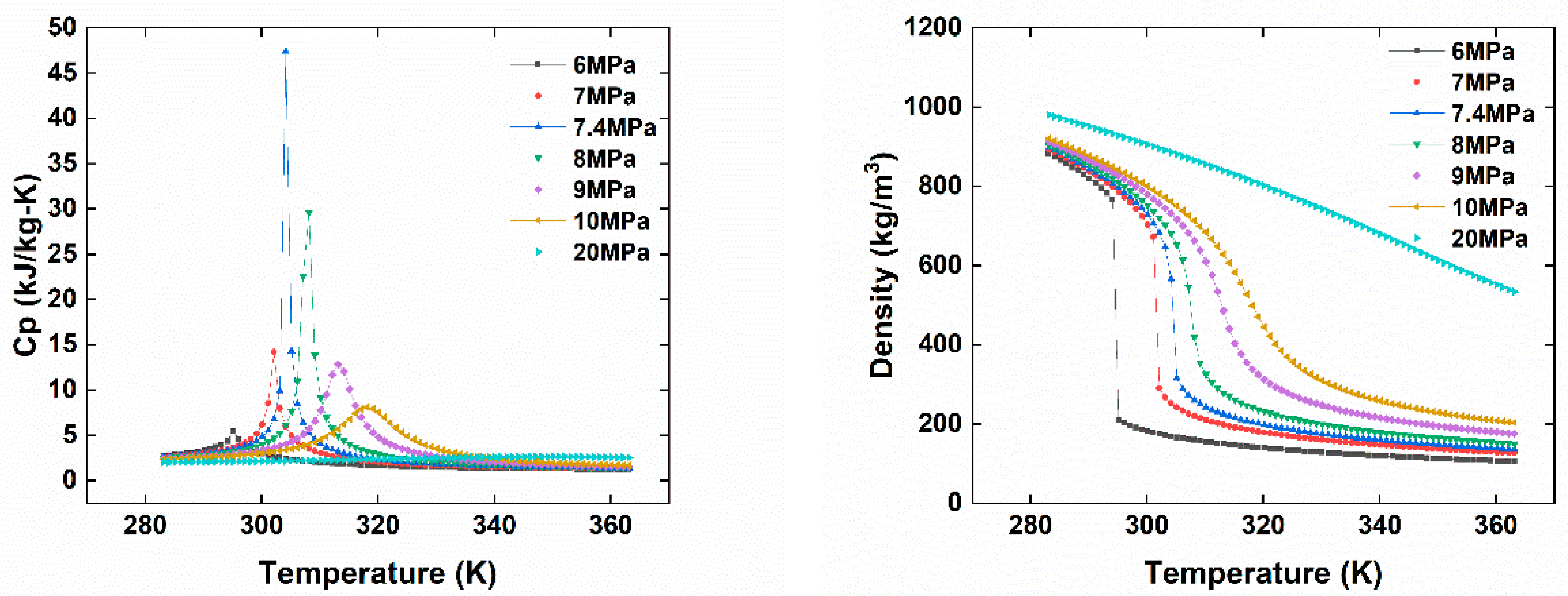
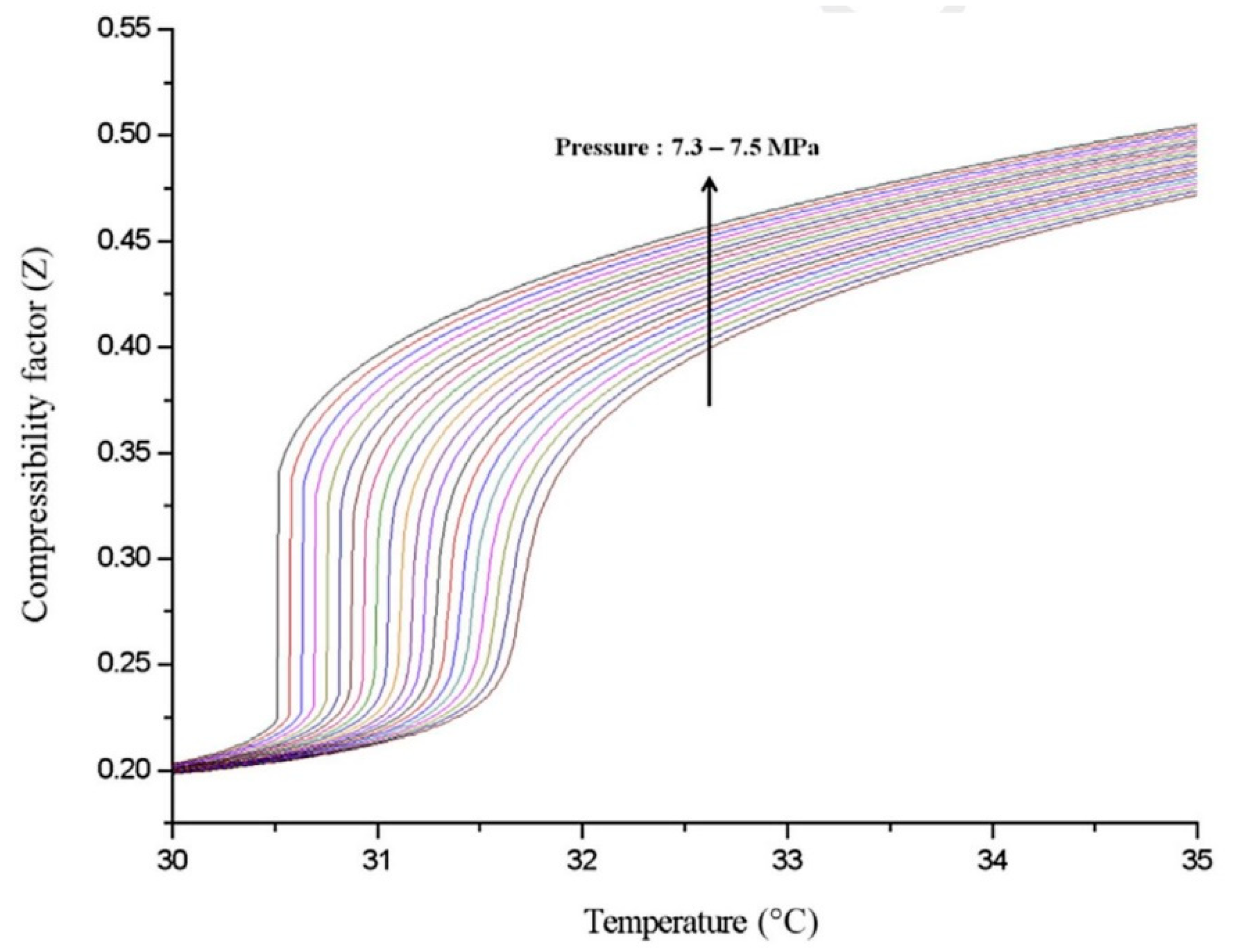
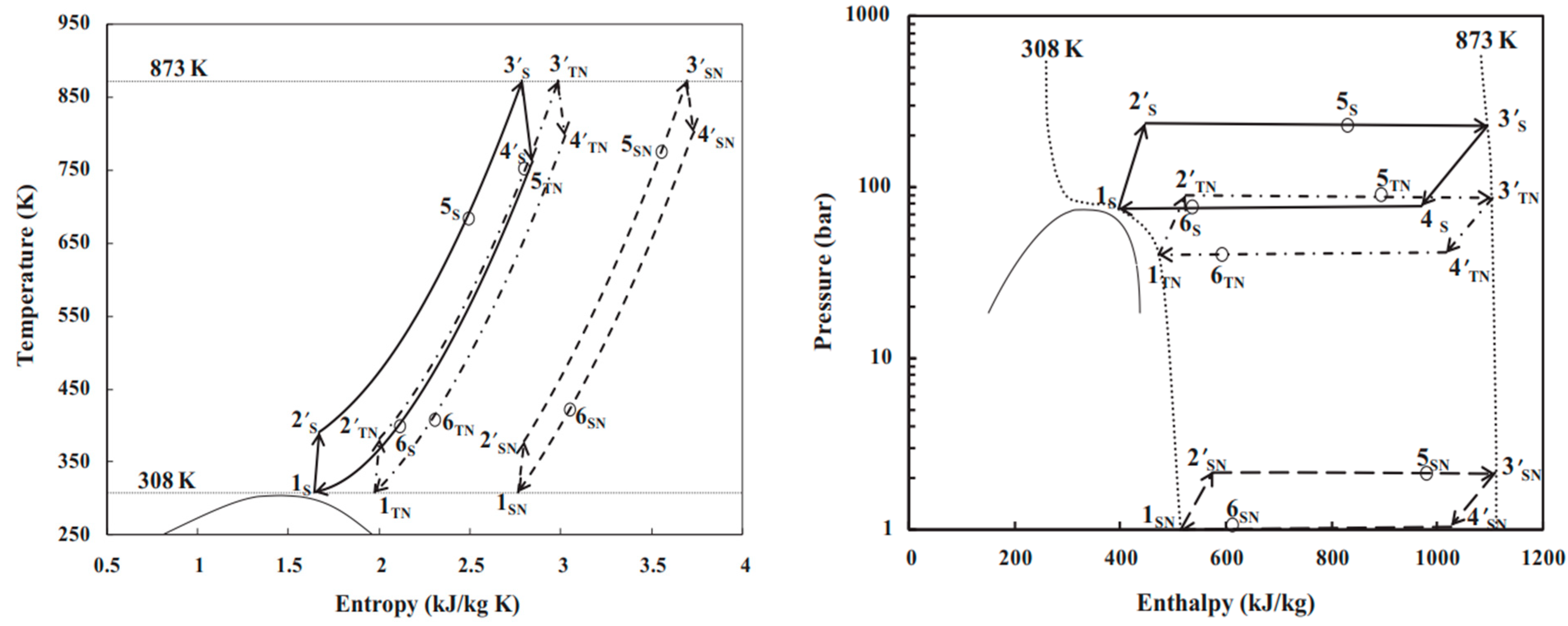
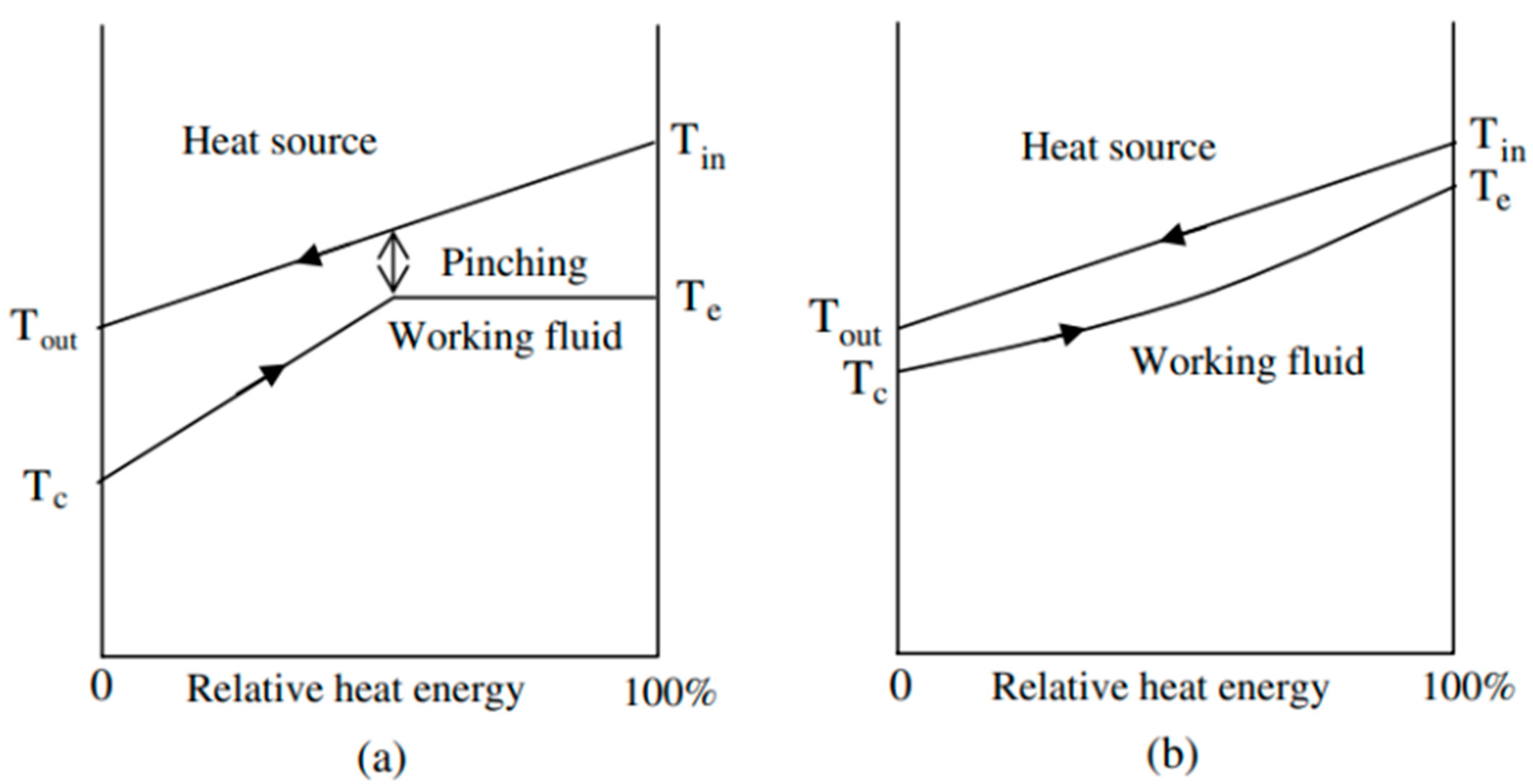
CO2 is a natural, non-toxic and non-flammable working fluid that possesses excellent thermophysical properties, including higher density, latent heat, specific heat, thermal conductivity and volumetric cooling capacity, along with lower viscosity [23]. These attributes make CO2 a significant player in various energy conversion systems. It has a low critical temperature of 31 °C but quite a high critical pressure of 7.4 MPa. As shown in Figure 1, near the pseudocritical region, the thermophysical properties of CO2 undergo rapid changes due to its high density and low compressibility factor close to its critical point. This leads to significant fluctuations in density and specific heat capacity with only slight variations in pressure or temperature. The compressibility factor is characterized as the ratio of the actual volume of a substance to its ideal volume. As observed in Figure 2, around the critical point, the compressibility factor of CO2 fluctuates between 0.2 and 0.5, which leads to a reduction in the power consumption of the compressor. Consequently, the S-CO2 cycle is distinguished by its high thermal efficiency, simple cycle configuration and compactness of system components. At the same power generation, the overall size of a steam Rankine cycle is estimated to be approximately four times larger than that of an S-CO2 Brayton cycle [17]. The benefits of utilizing CO2 working fluid in thermodynamic cycles include (1) environmentally friendly nature, with no ozone-depleting potential (ODP) and neglectable global warming potential (GWP = 1), (2) abundance, non-toxicity and non-combustibility, (3) non-reactivity with component materials, and (4) superb thermodynamic and transport properties. According to the low critical temperature of CO2 working fluid, its associated thermodynamic cycle can easily traverse both subcritical and supercritical regions with high-temperature heat sources, naming the cycles as either transcritical or supercritical cycles. Three options exist for utilizing CO2 in the Brayton cycle as shown in Figure 3: (1) the classic cycle (‘SN’), which operates entirely under critical pressure, known as the subcritical cycle; (2) the transcritical cycle (‘TN’), the highest pressure operates above critical pressure, allowing CO2 to pass through both subcritical and supercritical regions; and (3) the supercritical cycle (‘S’), which operates entirely above the critical pressure. However, the difference between the transcritical and supercritical Rankine cycles is not strict. The transcritical Rankine cycle, under some conditions, can also be called the supercritical Rankine cycle. The concept of the supercritical CO2 Rankine cycle pertains to the situation where heat addition happens at CO2 pressure above the critical point, while heat rejection occurs at CO2 pressure below the critical point, as illustrated in Figure 4. It has been demonstrated that the efficiency of the S-CO2 Brayton cycle surpasses that of the superheated steam Rankine cycle when the turbine inlet temperature exceeds 470 °C [24]. The potential for maximizing power output in an ORC is hindered by the evaporation process with constant temperature, making it a less favourable option for sensible heat sources. By avoiding the isothermal boiling process, CO2 in the transcritical/supercritical cycle achieves a more effective thermal match with the heat source, thereby attaining higher thermal efficiency compared to ORC, as depicted in Figure 5. The issue of pinching points between the heat source and working fluid temperature along the heat exchanger is effectively addressed by utilizing a transcritical or supercritical CO2 cycle.
Energies 16 07781 g001
Figure 1. CO2 thermal–physical properties vary with temperature at different pressures.
Energies 16 07781 g002
Figure 2. CO2 compressibility factor [17].
Energies 16 07781 g003
Figure 3. P-H diagram and T-S diagram of subcritical, transcritical and supercritical CO2 Brayton cycles: SN–subcritical; TN–transcritical; S–supercritical [25].
Energies 16 07781 g004
Figure 4. Configuration and processes of a CO2 supercritical Rankine cycle. (a) The configuration. (b) The process in a T–S diagram [26].
Energies 16 07781 g005
Figure 5. Diagram illustrating the heat transfer between the heat source and working fluid in the high-temperature main heat exchanger: (a) ORC cycle. (b) CO2 transcritical/supercritical power cycle [27].

This entry is adapted from the peer-reviewed paper 10.3390/en16237781

References

  1. Energy Institute. Statistical Review of World Energy; Energy Institute: London, UK, 2023.
  2. Schuster, A.; Karellas, S.; Kakaras, E.; Spliethoff, H. Energetic and Economic Investigation of Organic Rankine Cycle Applications. Appl. Therm. Eng. 2009, 29, 1809–1817.
  3. Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Low-Grade Heat Conversion into Power Using Organic Rankine Cycles—A Review of Various Applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979.
  4. Coco-Enríquez, L.; Muñoz-Antón, J.; Martínez-Val, J.M. New Text Comparison between CO2 and Other Supercritical Working Fluids (Ethane, Xe, CH4 and N2) in Line- Focusing Solar Power Plants Coupled to Supercritical Brayton Power Cycles. Int. J. Hydrogen Energy 2017, 42, 17611–17631.
  5. Manzolini, G.; Binotti, M.; Bonalumi, D.; Invernizzi, C.; Iora, P. CO2 Mixtures as Innovative Working Fluid in Power Cycles Applied to Solar Plants. Techno-Economic Assessment. Sol. Energy 2019, 181, 530–544.
  6. Besarati, S.M.; Yogi Goswami, D. Analysis of Advanced Supercritical Carbon Dioxide Power Cycles with a Bottoming Cycle for Concentrating Solar Power Applications. J. Sol. Energy Eng. 2013, 136, 010904.
  7. Sulzer, G. Verfahren zur erzeugung von arbeit aus warme. Swiss Pat. 1950, 269599, 15.
  8. Feher, E.G. The supercritical thermodynamic power cycle. Energy Convers. 1968, 8, 85–90.
  9. Angelino, G. Perspectives for the Liquid Phase Compression Gas Turbine. J. Eng. Power 1967, 89, 229–236.
  10. Angelino, G. Carbon Dioxide Condensation Cycles for Power Production. J. Eng. Power 1968, 90, 287–295.
  11. Angelino, G. Real Gas Effects in Carbon Dioxide Cycles. In Proceedings of the ASME 1969 Gas Turbine Conference and Products Show, Cleveland, OH, USA, 9–13 March 1969.
  12. Brun, K.; Friedman, P.; Dennis, R. Fundamentals and Applications of Supercritical Carbon Dioxide (SCO2) Based Power Cycles; Woodhead Publishing: Cambridge, UK, 2017.
  13. Le Moullec, Y. Conceptual Study of a High Efficiency Coal-Fired Power Plant with CO2 Capture Using a Supercritical CO2 Brayton Cycle. Energy 2013, 49, 32–46.
  14. Mecheri, M.; Le Moullec, Y. Supercritical CO2 Brayton Cycles for Coal-Fired Power Plants. Energy 2016, 103, 758–771.
  15. Xu, J.; Wang, X.; Sun, E.; Li, M. Economic Comparison between SCO2 Power Cycle and Water-Steam Rankine Cycle for Coal-Fired Power Generation System. Energy Convers. Manag. 2021, 238, 114150.
  16. Wang, Z.; Xu, J.; Wang, T.; Miao, Z.; Wang, Q.; Liu, G. Performance of SCO2 Coal-Fired Power Plants at Various Power Capacities. J. Clean. Prod. 2023, 416, 137949.
  17. Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of Supercritical CO2 Power Cycle Technology and Current Status of Research and Development. Nucl. Eng. Technol. 2015, 47, 647–661.
  18. Dostal, V.; Driscoll, M.J.; Hejzlar, P. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors. Doctoral Dissertation, Department of Nuclear Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004.
  19. Moisseytsev, A.; Sienicki, J.J. Investigation of Alternative Layouts for the Supercritical Carbon Dioxide Brayton Cycle for a Sodium-Cooled Fast Reactor. Nucl. Eng. Des. 2009, 239, 1362–1371.
  20. Wright, S.A.; Conboy, T.M.; Radel, R.; Rochau, G.E. Modeling and Experimental Results for Condensing Supercritical CO2 Power Cycles; OSTI OAI (U.S. Department of Energy Office of Scientific and Technical Information): Oak Ridge, TN, USA, 2011.
  21. Yoon, H.J.; Ahn, Y.; Lee, J.I.; Addad, Y. Potential Advantages of Coupling Supercritical CO2 Brayton Cycle to Water Cooled Small and Medium Size Reactor. Nucl. Eng. Des. 2012, 245, 223–232.
  22. World Nuclear Performance Report 2023. Available online: https://www.world-nuclear.org/getmedia/0156a8d7-01c6-42d9-97be-3f04f34cb8fa/performance-report-2023-final.pdf.aspx (accessed on 1 September 2023).
  23. Ge, Y.T.; Tassou, S.A.; Santosa, I.D.; Tsamos, K. Design Optimisation of CO2 Gas Cooler/Condenser in a Refrigeration System. Appl. Energy 2015, 160, 973–981.
  24. Dostal, V.; Hejzlar, P.; Driscoll, M.J. The Supercritical Carbon Dioxide Power Cycle: Comparison to Other Advanced Power Cycles. Nucl. Technol. 2006, 154, 283–301.
  25. Garg, P.; Kumar, P.; Srinivasan, K. Supercritical Carbon Dioxide Brayton Cycle for Concentrated Solar Power. J. Supercrit. Fluids 2013, 76, 54–60.
  26. Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A Review of Thermodynamic Cycles and Working Fluids for the Conversion of Low-Grade Heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067.
  27. Chen, Y.; Lundqvist, P.; Johansson, A.; Platell, P. A Comparative Study of the Carbon Dioxide Transcritical Power Cycle Compared with an Organic Rankine Cycle with R123 as Working Fluid in Waste Heat Recovery. Appl. Therm. Eng. 2006, 26, 2142–2147.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback