Estimation of Muckpile Fragmentation Methods: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Hajime Ikeda
,
Taiga Sato
,
Kohei Yoshino
,
Hisatoshi Toriya
,
Hyongdoo Jang
,
Tsuyoshi Adachi
,
Itaru Kitahara
,
Youhei Kawamura

Blasting is a very effective method of crushing various types of rocks with different hardness in mining, as it can crush a large amount of rocks at once and at a low cost. In addition, muckpile fragmentation is represented by particle size distribution, which is an important parameter for optimizing blasting plans. Methods for measuring the particle size distribution of muckpile fragmentation include sieving and using laser scanners, and methods using 2D images.

  • muckpile
  • particle size distribution
  • deep learning
  • Blasting

1. Introduction

Blasting is a process of breaking rock mass using explosives, such as in mining, and the resulting pile of broken rock is called muckpile fragmentation. The main purpose of blasting is to break rocks into suitable sizes without damaging surrounding objects and to extract resources contained in the rocks [1]. Blasting is a very effective method of crushing various types of rocks with different hardness in mining, as it can crush a large amount of rocks at once and at a low cost. In addition, muckpile fragmentation is represented by particle size distribution, which is an important parameter for optimizing blasting plans [2].
Currently, methods for measuring the particle size distribution of muckpile fragmentation include sieving and using laser scanners [3], and methods using 2D images [4]. However, sieving requires a tremendous amount of effort to be performed on site, as the amount of rocks that can be measured at once is limited. The cost and knowledge required for laser scanners pose problems when used on site. Therefore, WipFrag [4] (https://wipware.com/products/wipfrag-image-analysis-software/, accessed on 4 September 2023), a method for quickly measuring particle size distribution by processing 2D images, has become more common. However, this method, which is based on 2D images, has been criticized for its low accuracy due to its inability to recognize the complex shapes of rocks [5]. Recent studies have underscored the pivotal role of blast charge initiation techniques in optimizing fragmentation outcomes and ensuring environmental safety, as evidenced by comprehensive analyses using the WipFrag software [6].

2. Related Work

2.1. Estimation for the Particle Size Distribution

The particle size distribution of blast muckpile has a significant impact on all downstream processes in the mining industry, including loading, hauling, and processing. Figure 2 illustrates the relationship between fragmentation size and unit cost, with the x-axis representing the fragmentation size and the y-axis representing the unit cost. If the fragmentation distribution is skewed towards smaller particles (part A), as shown in Figure 1, useful minerals become excessively fine, resulting in increased costs. Conversely, if the particle size distribution is skewed towards larger particles (part C), transportation becomes challenging and additional mechanical crushing is required after blasting, leading to unnecessary costs. To minimize total costs, blasting should be conducted in a manner that achieves an optimal particle size distribution (aiming at part B). However, controlling blasting is complex, as it depends on various factors such as the amount and type of explosives, the number and depth of blasting holes, and the timing of blasting. Consequently, accurate estimation of the particle size distribution of blast muckpile is essential for optimizing downstream processes, prompting researchers to propose various mathematical models for this purpose, such as the Kuz-Ram mathematical model presented by Cunningham [7], the Swebrec model proposed by Sanchidrian et al. [8], and the Hybrid model introduced by Gheibie et al. [9].
n = 2.2 − 14 B D 1 + S l B 2 1 − W B × a b s B C L − C C L L + 0.1 0.1 L H
where, B: burden (m), S: spacing (m), D: hole diameter (mm), W: standard deviation of drilling precision (m), L: charge length (m), 𝐵𝐶𝐿: bottom charge length (m), 𝐶𝐶𝐿: column charge length (m), H: bench height (m).
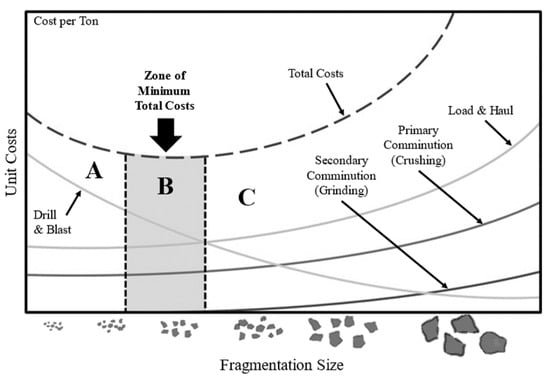
Applsci 13 10985 g002
Figure 1. Relationship between Fragmentation Size and Operational Costs in Mining.
The Kuz-Ram mathematical model is a common mathematical model for predicting the size distribution of rock fragments caused by blasting. It is widely used in the mining industry because of the ease of collecting input data and the simplicity of the relationship between blasting design and rock fragmentation results. However, one limitation of this predictive mathematical model is that it tends to underestimate the number of fines produced by the blast, which means it cannot be considered a perfect estimation model. The distinction between 2D and 3D imaging in fragmentation estimation lies in the spatial information captured. 3D imagery, with its depth and volume metrics, provides a comprehensive representation of muckpile fragments. The model is specifically designed to leverage this depth of information inherent in 3D data, allowing for a refined fragmentation estimation process. In the diagram illustrating the relationship between fragmentation size and operational costs in mining, depicted in Figure 1, three zones labeled A, B, and C are shown. In zone A, excessive fragmentation leads to increased costs due to the heightened need for drilling and blasting. Conversely, in zone C, while costs for drilling and blasting are diminished, there is a substantial rise in the subsequent transportation and additional crushing expenses. Zone B stands as the optimal middle ground, highlighting the zone of minimum total costs. Here, both the preliminary and subsequent costs converge to provide the most economical mining operation.

2.2. Estimation Methods Using 2D Images

The rapid advancement of image analysis technology has enabled the development of methods for estimating particle size distribution using image analysis. WipFrag, for instance, is a system that estimates the particle size distribution of blast muckpile using digital image analysis and videotape images [4]. Despite its ease of use and widespread application in mining sites, several drawbacks have been identified with this estimation method. The automatic contouring tool built into the 2D image processing system requires manual correction, making it less user-friendly. This process can be time-consuming and prone to human error, leading to potential inaccuracies in the estimated particle size distribution [10]. Additionally, the quality of the input images has a significant impact on the accuracy of the estimation. Factors such as lighting conditions, camera angle, and image resolution can all influence the reliability of the results [11].
Furthermore, estimating the particle size distribution of the entire blast muckpile necessitates the analysis of multiple moving photographs, each requiring calibration. The process of calibrating multiple images can be cumbersome, and the complexity increases with the number of images involved [12]. The overlapping nature of blast muckpile and the potential for particles to be too small for recognition can lead to overestimation of particle size distribution [13]. In an effort to address these limitations, researchers have proposed alternative methods, such as those based on stereoscopic imaging and 3D reconstruction [2][14]. These approaches aim to improve the accuracy of particle size distribution estimation by leveraging the additional depth information provided by multiple images or 3D models. However, these methods can also be more computationally intensive and may require specialized equipment, potentially limiting their widespread adoption in the mining industry.

2.3. Estimation Using 3D Images

Recent advancements in muckpile fragmentation estimation have shifted from traditional 2D imaging systems to more advanced 3D model-based techniques [15][16]. A approach harnesses the power of Structure-from-Motion (SfM), a state-of-the-art 3D photogrammetry method [2][17], combined with Patch-based Multi-View Stereo (PMVS) [4][18]. This methodology allows for the detailed reconstruction of muckpile’s 3D shape, subsequently facilitating the estimation of its particle size distribution.
The process further categorizes clusters based on specific thresholds. When a point surpasses a predetermined boundary threshold between two clusters, these clusters are distinguished as separate rocks. Conversely, if no points exceed this threshold, clusters are identified as the same rock, merging them. A significant challenge arises here, as the number of clusters doesn’t always equate to the actual number of rocks. This disparity complicates the precise measurement of particle size distribution, especially when aiming to consolidate multiple clusters representing a single rock.
One approach to addressing the challenge of accurately measuring the particle size distribution is to use a combination of machine learning techniques, such as deep learning and convolutional neural networks (CNNs), to improve the detection and segmentation of rocks within the 3D point cloud [19][20]. These methods have been successfully applied in various fields, including object recognition, image segmentation, and 3D point cloud processing. By training a model with a large dataset of labeled 3D point clouds, the deep learning algorithms can learn to identify and segment rocks more accurately, potentially improving the estimation of the particle size distribution.
Another possibility is to integrate other sources of information, such as LiDAR data, to enhance the accuracy of the 3D models and the subsequent particle size distribution estimation [21][22]. By combining different types of data, more accurate and robust models can be generated, leading to improved estimations of the particle size distribution and better optimization of downstream processes in the mining industry.

This entry is adapted from the peer-reviewed paper 10.3390/app131910985

References

  1. Takahashi, Y.; Yamaguchi, K.; Sasaoka, T.; Hamanaka, A.; Shimada, H.; Ichinose, M.; Kubota, S.; Saburi, T. The Effect of Blasting Design and Rock Mass Conditions on Flight Behavior of Rock Fragmentation in Surface Mining. J. Min. Mater. Process. Inst. Jpn. 2019, 135, 94–100.
  2. Adebola, J.M.; Ajayi, O.D.; Elijah, P. Rock Fragmentation Prediction Using Kuz-Rum Model. J. Environ. Earth Sci. 2016, 6, 110–115.
  3. Fragmentation Analysis. Maptek. Available online: https://www.maptek.com/products/pointstudio/fragmentation_analysis.html (accessed on 15 January 2023).
  4. Norbert, M.; Palangio, T.; Franklin, J. WipFrag Image Based Granulometry System. In Proceedings of the FRAGBLAST 5 Workshop on Mearsurement of Blast Fragmentation, Montreal, QC, Canada, 23–24 August 1996; pp. 91–99.
  5. Norbert, M.; Palangio, C. WipFrag System 2-Online Fragmentation Analysis. In Proceedings of the FRAGBLAST 6, 6th International Symposium for Rock Fragmentation by Blasting, Johannesburg, South Africa, 8–12 August 1999; pp. 111–115.
  6. Taiwo, B.O.; Fissha, Y.; Palangio, T.; Palangio, A.; Ikeda, H.; Cheepurupalli, N.R.; Khan, N.M.; Akinlabi, A.A.; Famobuwa, O.V.; Faluyi, J.O.; et al. Assessment of Charge Initiation Techniques Effect on Blast Fragmentation and Environmental Safety: An Application of WipFrag Software. Mining 2023, 3, 532–551.
  7. Cunningham, C. Fragmentation Estimation and the Kuz-Ram model—Four Years On. In Proceedings of the 2nd International Symposium on Rock Fragmentation by Blasting, Keystone, CO, USA, 23–26 August 1987.
  8. Sanchidrian, J.A.; Segarra, P.; Lopez, L.M.; Domingo, F.J. A model to predict the size distribution of rock fragments. Int. J. Rock Mech. Min. Sci. 2009, 46, 1294–1301.
  9. Gheibie, S.; Aghababaei, H.; Hoseinie, S.H. Development of an empirical model for predicting rock fragmentation due to blasting. In Proceedings of the 9th International Symposium on Rock Fragmentation by Blasting, Granada, Spain, 13–17 August 2009; pp. 453–458.
  10. Thornton, C.; Krysiak, Z.; Hounslow, M.J.; Jones, R. Particle size distribution analysis of an aggregate of fine spheres from a single photographic image. Part. Part. Syst. Charact. 1997, 14, 70–76.
  11. Palangio, T.; Pistorius, C. On-line analysis of coarse material on conveyor belts. Min. Eng. 2000, 52, 37–40.
  12. Gharibi, R.; Swift, S.J.; Booker, J.D.; Franklin, S.E. Particle size distribution measurement from millimeters to nanometers and from rods to platelets. J. Colloid Interface Sci. 2011, 361, 590–596.
  13. Coope, R.; Onederra, I.; Williams, D. Image analysis of rock fragmentation: A review. Int. J. Min. Sci. Technol. 2017, 27, 171–180.
  14. Segui, X.; Arroyo, P.; Llorens, J. Automated estimation of particle size distributions from 3D image data. In Proceedings of the Conference on Applications of Digital Image Processing XXXIII, San Diego, CA, USA, 2–4 August 2010; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; Volume 7799, p. 77990P.
  15. Cunningham, C. The Kuz-Ram Fragmentation Model-20 Years On. In Proceedings of the European Federation of Explosives Engineers, Brighton, UK, 13–16 September 2005; pp. 201–210.
  16. Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. Structure-from-Motion photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314.
  17. James, M.R.; Robson, S. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Process. Landf. 2014, 39, 1769–1788.
  18. Furukawa, Y.; Ponce, J. Towards internet-scale multi-view stereo. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1434–1441.
  19. Shi, S.; Wang, Q.; Xu, P.; Chu, X. VoxNet: A 3D Convolutional Neural Network for Real-Time Object Recognition. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 922–928.
  20. Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. TOG 2019, 38, 1–12.
  21. Fowler, M.J.; Henstock, T.J.; Schofield, D.I. Integration of terrestrial and airborne LiDAR data for rock mass characterization. J. Appl. Remote Sens. 2013, 7, 073506.
  22. Varshosaz, M.; Khoshelham, K.; Amiri, N. Integration of terrestrial laser scanning and close range photogrammetry for 3D modeling of an open-pit mine. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 365–372.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback