Pitch Control Technique for Horizontal Axis Wind Turbines: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Amira Elkodama
,
Amr Ismaiel
,
A. Abdellatif
,
S. Shaaban
,
Shigeo Yoshida
,
Mostafa A. Rushdi

In recent years, the increasing environmental problems, especially the issue of global warming, have motivated demand for a cleaner, more sustainable, and economically viable energy source. In this context, wind energy plays a significant role due to the small negative impact it has on the environment, which makes it among the most widespread potential sustainable renewable fuel nowadays. However, wind turbine control systems are important factors in determining the efficiency and cost-effectiveness of a wind turbine (WT) system for wind applications.

  • pitch control
  • renewable energy
  • torque control
  • yaw control
  • wind turbine

1. Introduction

Recently, non-renewable energy sources have increasingly been causing environmental pollution, which is one of the most serious challenges worldwide. Over 70% of the energy used in industry is from non-renewable sources that have a serious impact on the environment and living organisms including humans [1]. These factors contribute to renewable energy development. Wind is one of the renewable energy sources that provide a solution to the environmental pollution problem as it has a much smaller pollution impact on the environment than non-renewable energy sources such as burning fossil fuels. It can be considered a competitive alternative to other conventional sources of electricity generation [2]. Wind energy has been attracting more attention in the world as it is a clean and sustainable energy source that is capable of keeping pace with the world’s ever-growing power needs.
Wind energy is leading the renewable energy market with installations that keep growing each year; 2021 was the second-best year ever for the global wind industry as it showed a year-over-year (YOY) growth of 12%, according to the Global Wind Energy Report of 2022. Almost 94 GW of wind power was installed, resulting in a global cumulative wind power capacity of up to 837 GW, with an increase of 153% compared to 2020 [3]. However, more installations are needed in order to reach the net zero target, the balance between greenhouse gas emissions produced vs. those taken out from the atmosphere by 2050.
Harvesting energy coming from the flowing air and converting it to electricity is performed conventionally through the utilization of a WT system [4]. WT converts the kinetic energy in the wind into mechanical energy by means of a rotor shaft connected to a generator that converts mechanical energy into electricity. The mechanical output power and torque of the WT depend on several factors such as wind speed, rotor swept area and the geometry of the turbine, blade pitch angle, turbine rotational speed, and turbine size. Equation (1) represents the output power of the WT.
where Pm is the WT’s mechanical power, ρ is the air density, Vw is the wind velocity in meters per second, and A is rotor area in meters. The power coefficient of the rotor or rotor efficiency (Cp) in the equation can be defined as the ratio between the actual obtained power and the maximum power available in the wind. The maximum value of the power coefficient derived based on 1D momentum theory is called the Betz limit. Cp varies with the TSR of the turbine (λ), which is the ratio between the blade tip speed and wind speed, and the pitch angle of the blades (β) and it is unique to each WT type. An example of a basic numerical model to show the relationship between various variables that affect the power coefficient of a wind turbine is shown in Equations (2)–(4) [5][6].
 
where β is the blade pitch angle, ωr is the rotational speed of the rotor in radians per second, and R is the rotor’s radius in meters.
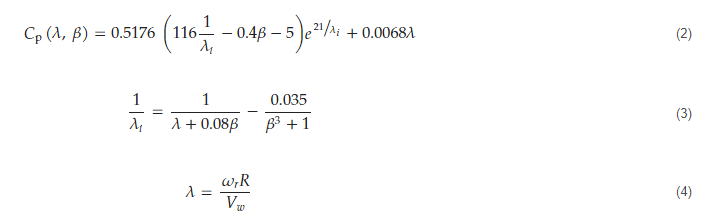
WTs are non-linear complex systems with flexible structures that are subjected to the wind that can vary dramatically in strength and direction, which in sequence effects the efficient harvesting of wind power. Modern horizontal axis wind turbines (HAWT) come in different sizes but generally, all types consist of several main components shown in Figure 1, which are: (1) the tower, the wind turbine’s supporting structure made of tubular steel; (2) the blade, a long fiberglass piece which catches the wind at the top of the wind turbine to turn the turbine; (3) the hub, a cast structure into which the blades are fitted and that is connected to the turbine’s main shaft; (4) the nacelle, which is a cover that houses the gearbox and generator connecting the rotor and tower.
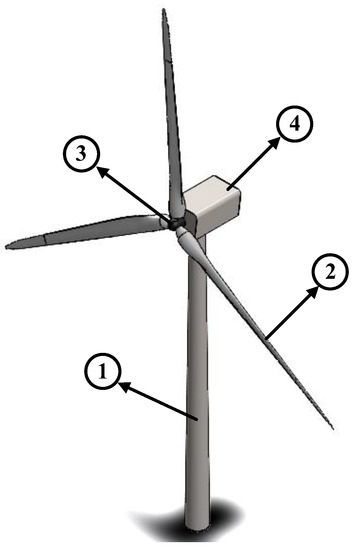
Energies 16 06394 g001
Figure 1. Wind turbine components.
However, low wind speeds result in low output power, while high wind speeds may cause the failure of most of the WT’s mechanical components [7]. Moreover, WTs are connected to a varying electrical grid with unpredictable voltage, frequency, and power flow fluctuations, hence the amount of power that can be executed from the wind, output power efficiency, cost, reliability, and availability strongly depend on the applied control strategy.
As WTs are becoming larger and more flexible, designing innovative control strategies to ensure the quality and stability of the power systems, besides decreasing wind energy cost by increasing the capture efficacy, becomes an explicit goal [8][9]. In addition, there are other main control objectives that need to be considered while designing a WT control system, such as energy capture maximization, mechanical load, and fatigue attenuation, providing damping, reliability, and availability that directly affect the cost and competitiveness of wind power technology [10][11]. Control can also be applied on the scale of wind farms to maximize power output through wake mitigation or other techniques [12]. There are many review articles that also consider WT size and design, different operating regions and different platforms (onshore and offshore) [13][14][15]. However, the scope of this work is control performed on the wind turbine components.
In a WT system, three types of controllers dominate, namely pitch angle control, torque control, and yaw alignment control. However, a study on the number of failures of turbines in a year has shown that the pitch control system is the first most common mechanical component contributing to an overall failure rate, followed by the yaw control system and then the torque control system [16][17].
Based on a WT’s power curve, shown in Figure 2, there are four main regions enclosed in two main areas. The actual power supplied to the WT grid is responsible for dividing the curve into two main areas, which are the above- and below-rated power areas. The main objective of the below-rated power area, where the wind speed is below the rated wind speed, is to maximize power capture, while in the above-rated power area, where the wind speed exceeds the rated wind speed, the objective is to maintain power at its rated value to avoid power fluctuations.
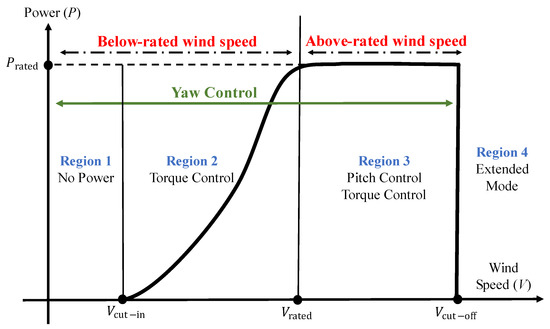
Energies 16 06394 g002
Figure 2. Power curve of a variable speed wind turbine.
Typically, the power curve of a utility-scale WT is divided to four operating regions depending on the wind speed value. In region 1, as the wind speed is less than the cut-in wind speed value (𝑣cut−in=3–4 m/s), there is not sufficient torque exerted on the turbine rotor to make it rotate with enough rotational speed to produce power. In region 2, also known as the transition region, the wind speed is between the cut-in speed and the rated speed value (𝑣rated=11–13 m/s). The objective is to obtain maximum aerodynamic efficiency through a torque controller that controls the generator’s synchronous speed so that the power produced grows rapidly reaching the rated/maximum power. In region 3, the rated power is maintained at a constant until the wind speed reaches the cut-off speed value (𝑣cut−off=25–30 m/s)), in this region the pitch angle control is needed to limit the incoming power or apply a braking mode to prevent WT structure fatigue by controlling the blade’s angle, which affects the rotor’s rotational speed (i.e., increasing the blade’s angle results in decreasing the rotational speed). Region 4, also known as the extended mode region, is where the wind speed exceeds the cut-off speed, so the rotor speed has to be controlled so as not to fatigue the WT’s components [18]. However, yaw control is applicable in all 4 regions, as it considers the wind direction change, so it is also applied to keep constant rated power output as it does not depend on the wind speed.

2. Pitch Control Technique

Pitch control is a system that operates and controls the pitch angle (β) of a WT blade by changing the aerodynamic forces on the blade at high wind speeds to limit rotor speed. The pitch control system, shown in Figure 3, is a closed loop control system that consists of the main controller that calculates the required pitch angle (𝛽𝑐) considering a set of conditions, transfers it to the pitch actuator system, which is made up either of gears and electric motors a or power supply system with hydraulic cylinders, and a wind speed sensor to give a feedback signal for the current wind conditions (𝜔𝑟). In the low wind speed region, the maximum power extraction mode is adapted, and the pitch angle is kept at its optimum operation, while in the high wind speed region, the rotor speed is accelerated so the pitch angle is adjusted to control the rotor speed to keep it within the controllable limit in order to produce stable power as well as keep the wind turbine in a safe operating environment.
Energies 16 06394 g003
Figure 3. Pitch control system.
Figure 4 shows the forces and wind effect on the blade’s airfoil. There are two methods to achieve zero rotor speed acceleration, which are pitch-to-feather, controlling the aerodynamic power captured by the blade (Pcaptured), and pitch-to-stall, controlling the output power of the generator (Pelectrical). The pitch-to-feather method is a common way to reduce the aerodynamic power resulting from very high wind speeds [18].
Energies 16 06394 g004
Figure 4. Airfoil pitch angle.
In [19], slow and fast pitching control rates at high wind speeds were investigated. The simulation results showed that if the pitch angle control is performed instantaneously, the speed can be kept constant by adjusting the difference between the captured power (Pcaptured) and electrical power (Pelectrical) to zero. Most large WTs use proportional–integral–differentiation (PID) or proportional–integral (PI) control for pitch angle control and power regulation. PID controllers are mostly used in industry to control a system, as they are feasible and easy to implement. They use closed-loop control feedback to keep the actual system’s output as close to the setpoint output as possible. To use PI/PID controllers, the parameters should be found, adjusted, and tuned according to the system’s behavior.
R. Karthik et al. implemented several methods for tuning a PID controller’s parameters, these are KP, KI, and KD, to study their impact on the system [20]. The performance of each method is represented in terms of the time domain performance index term and the parameters of interest are delay time (Td), peak time (Tp), rise time (Tr), settling time (Ts), peak overshoot (Mp in %), and steady-state error (ess). Evaluating the response efficacy of each method was based on giving/producing the lower values for the mentioned parameters. Simulation results showed that among all the PID parameters tuning methods, the Zeigler–Nicholas method gives better performance in terms of time delay, settling time, and peak overshoot compared to the other methods, hence is the use of this method is recommended for tuning the PID controller’s parameters in WT application.
Clemens Jauch et al. designed a PID pitch angle controller for a fixed speed active-stall WT, which has only a pitch system to control the output power, by deriving the transfer function (TF) of the WT system from its step response using the root locus method [21]. The TF of the WT was of a very high order due to the system’s non-linearities so it has been defined as sets of 2nd-order TFs. Steady-state error was avoided by adding an integrator to the system. A pole was added at the origin of the s-plane to deform the locus, preventing the root locus from crossing the previously found point for the dynamic response, so the WT’s performance became significantly better despite the limitations of the pitch system.
Richie Gao and Zhiwei Gao designed an effective PI pitch controller to overcome the effect of delays caused by hydraulic pressure-driven units that affect the pitch control systems [22]. In order to estimate the PI controller parameters, a direct search optimization technique was applied to assume no delays in the WT. The input and output of the controlled system are used to design a delay estimator to estimate the disturbances caused by the delay, then subtract this estimated delay from the WT’s output to give compensated output used for feedback loop control, to remove the effect of the delays. The applied controller showed reliable improvement of the WT control system without the need for prior knowledge of the system delays.
Since PID parameters are unknown and calculated by numerous complex techniques, Atif Iqbal et al. have proposed a developed particle swarm optimization (PSO) algorithm with fminsearch in order to provide optimal parameters for the PID pitch controller to stabilize the WT’s power output [23]. The developed PSO algorithm showed improvement in the system’s stabilization in different aspects from rising time to settling time. By comparing the proposed algorithm to conventional PSO, the simulation results indicated a higher output power and a limit on the rotor speed, along with mechanical torque. Also, Sachin Goyal et al. developed a neuro-fuzzy (NF) tuned PID pitch controller for an individual pitch controller–variable speed wind turbine (IPC–VSWT) to quickly maintain the output power in line with wind speed fluctuations [24]. Comparison between untuned PID and NF-tuned PID showed a performance improvement for the proposed algorithm regarding overshoot percentage and settling time by 15% and 37%, respectively, compared to untuned PID.
There are recent optimization methods that have been used for PI/PID controller parameter tuning. Shi-Jie Jiang et al. proposed a recent Archimedes optimization algorithm (AOA) based on the Taguchi parallel method (TPAOA), which has few parameters to solve, is easy to implement, and has an easy-to-understand interface for PID parameter tuning [25]. Using the parallel mechanism and Taguchi orthogonal solved the drawbacks of the optimization algorithm and showed competitive optimization results compared to other algorithms represented in the CEC2017 test suite and also smoothed the WT’s output power by reducing the impact of wind speed fluctuations on the system.
In [26], the firefly algorithm (FA) for PID pitch control parameter tuning was proposed. The FA was improved by applying a hybrid parallel compact technique that helps in finding better solutions with minimum errors and saves more operation memory. The parallel compact firefly algorithm (PCFA) was compared to the original FA and the results showed the superiority of the PCFA in smoothing the output power in a shorter calculation time and using less operation memory. Also, in [27] the grey wolf optimization (GWO) algorithm for the PI-MPPT controller gains tuning was proposed by considering integral time-multiplied square error (ITSE) minimizing, which is developed from SCIG power error regarding region 3. The GWO algorithm provided optimal performance for PI tuning compared to the genetic algorithm (GA) and PSO algorithms.
Soft computing techniques are algorithms that deal with imprecision, approximation, and uncertainty as they can provide an approximate solution for complex and non-linear systems with non-exact models effectively. The maximum power point tracking (MPPT) technique is considered to be a soft computing method as it deals with a non-exact system model and it relies on achieving the best control action that investigate the best performance, so choosing the appropriate MPPT algorithm is an important factor for system performance enhancement [28].
Fuzzy logic control (FLC) is a soft computing technique and mathematical based system that converts and analyzes analog data in terms of logical variables by assigning a specific output according to the state of the input, so it can deal with complex nonlinear control situations. FLC is easier, cheaper, and more robust than a PID controller in that it can cover a wide range of operation points for a dynamic system. Tan Luong Van et al. presented an FLC Sugeno-type application to improve the wind energy captured by a 2-MW wind turbine at rated wind speed for a variable speed variable pitch (VSVP) WT [29]. The controller is implemented by taking the generator output power and generator speed instead of wind speed as inputs to the controller, while the output is the reference pitch angle βref. In the partial-load region, Pref is determined by the MPPT control strategy, while in the full-load region, Pref is set to Prated, the FLC finds βref by determining inputs, setting up rules, and converts the results into output signals. Experiments and simulation showed that FLC gives 5.097%, 2.043%, and 3.065% higher output power than that of PI controllers with and without gain scheduling, and PID controllers, respectively, and also could maintain output power and speed at high wind speeds.
FLC showed an improved performance also for small WTs, M.A.M. Prats et al. presented a computational fuzzy pitch controller model for 600 kW VSVP wind turbines to improve the captured energy at low, rated, and high wind speeds and compared its performance to the PI linear controller [30]. The simulation results at rated wind speed showed a 1.9% increase in energy capture with the fuzzy controller compared to the PI controller and better speed and blade pitch control was observed compared to the conventional linear controller. These results declare an improved transition between power limitation in the full-load region and power optimization in the partial-load region. F. Scherillo et al. also designed a fuzzy logic-based pitch control for a 60 kW mini wind turbine and investigated its performance for different turbulence and wind intensities [31]. The simulation showed good results in terms of rotor speed and power production variability compared to the PID controller based on the Ziegler–Nichols rule.
For FLC optimization, Zafer Civelek proposed an advanced intelligent genetic algorithm (AIGA) with new features that enhance the algorithm’s performance such as the addition of an acceptable error concept (AEC) [32]. In order to adjust the coefficient of normalization, denormalization, and FLC values, the conversion from decimal to binary and from binary to decimal is determined based on this acceptable error. For better performance, the selection of crossover which enables the production of new individuals from two individuals with high fitness values and also affects the time that the GA reaches the goal was 90%. Benchmark functions are used for performance analysis and comparison between GA, IGA, and AIGA and the results showed that AIGA reaches the desired results in iterations equal to 75 while the GA and IGA iterations number is 1000, and also reaches 1000 optimum results for all of the test functions, which will helps to increase the WT’s output power stability.
FLC can provide an alternative approach to tune and adjust PID controller parameters by utilizing a set of if–then rules to overcome the problem of PI/PID controller and handle the dynamically changing operating points of the WT system and also increase the power system stability of the WT. Minh Quan Duong et al. have presented a hybrid controller of PI and FLC techniques in order to smooth wind power fluctuations and drop output power at high wind speeds [33]. The conventional PI controller’s purpose was to linearize the model by regulating the output according to a relative error between mechanical power (Pmech) and nominal power (Pnom), where the ε = (Pmech − Pnom)/Pnom and its parameter gain are chosen based on Ziegler–Nicholas equations. In order to improve the generator’s disturbance and damping characteristics, a fuzzy logic technique was proposed. The power error was represented by three linguistic variables, negative (N), zero (Z), and positive (P), and for the output, nine memberships were used. After the fuzzy sets are defined, the control strategy is defined by a set of if–then rules. The simulation results showed an improvement in power quality rather than using a PI controller only.
Lin Pan and Xudong Wang also proposed a repetitive control combined with a Takagi–Sugeno fuzzy PID pitch controller in order to stabilize the output power [34]. However, in [35] a comparison between three control schemes for the WT pitch control system was proposed, which are PID, fuzzy, and fuzzy–PID regarding generator power, torsional torque, and generator speed in the above-rated wind speed region. The PID controller had a higher deviation in the three comparison aspects, while fuzzy and fuzzy–PID showed remarkable power fluctuation reduction and also a reduction in torsional torque. However, fuzzy–PID gave the best results in improving the system’s performance.
Asif Rashid and Deng Ying developed logical fuzzy control inference (FCI) which is a non-linear method that uses if–then fuzzy rules set along with “OR” or “AND” connectors [36]. This control model automatically adjusts the β angle to measure rotor speed so as to increase power production. So, by applying the FCI control method based on Mamdani rules with a PI(D) controller which controls the variation in rotor speed by correcting the error between the output and the desired input, a promising result of maximizing captured power and economically efficient energy performance have been achieved.
In [37], a novel approach for pitch control based on an adaptive neuro-fuzzy inference system for obtaining effective wind velocity with no need for a sensor and sliding mode observer to estimate the aerodynamic torque was proposed. This approach aimed to control output power and rotor speed optimally in the over-rate wind speed region which increases the life of the WT. Simulations for fore–aft tip displacement showed a decrease in its STD value by 50%.
Since modern WT control systems depend mainly on their actuators, there are some constraints that should be considered like actuator limitations, system constraints due to system non-linearities, and the intermittency of integrating wind power into the electric grid. It is important to recognize that both the generator torque and the blade pitch angle have limitations in absolute values and change rates, but the limitation of blade pitch actuators is the more critical one of these. The prediction control technique can analyze current and historical data to make a prediction about the future output knowing the system’s input and constraints. Several forecasting techniques considering different time scales were reviewed and discussed in [38] showing the major challenges associated with wind power prediction and the different mechanisms to determine the best available. Since wind turbine operation has a periodic nature, the direct inclusion of the constraints in the control algorithm for individual pitch control shows a non-continuity optimization problem, so Vlaho Petrovic et al. proposed a constraints inclusion method by transforming wind turbine constraints into a d-q coordinate system to ensure the continuity of the constraints in the system model [39].
Ahmed Lasheen and Abdel Latif Elshafei designed a model predictive control (MPC) algorithm that depends on the system model for predicting the future output over a selected horizon. The MPC algorithm was designed based on a Takagi-Sugeno fuzzy model for its ability to control multivariable systems subjected to constraints [40]. Linearized models have been produced by the open-source software FAST at determined operating points depending on wind speed variation, each produced model represents a fuzzy rule, so in order to reduce the number of fuzzy rules to ease calculations, the gap metric concept was applied resulting in a total of six linearized models at wind speed range from 12 to 22 m/s with 2 m/s step. A fuzzy MPC algorithm was also used in [41] to reduce the blades’ flip-wise deflections and regulate the output power of the WT in region 3, considering the generator fluctuations. Compared to the gain scheduled PI (GSPI) baseline controller, FMPC showed better performance regarding less settling time and overshoot, less computational time, and mechanical load reduction. The overall fuzzy model, after blending all rules, is a time-varying linear model that can predict the future output and states by applying MPC to it.
Another prediction algorithm is the feedforward technique which considers solutions for improving the situation in the future rather than considering positive or negative feedback. P. Venkaiah and Bikash K. Sarkar proposed a fuzzy feedforward PID pitch controller developed through an electrohydraulic pitch actuation system which has merits of high power-to-weight ratio, self-lubricating, etc. [42]. The feedforward technique estimates the output of the WT system from the PID control algorithm, which minimizes the error between the desired and current state of the system without waiting for the PID response.
In [43], a hybrid artificial intelligence and advanced control technique for the VSWT pitch control system is introduced. Wind speed prediction based on support vector regression (SVR) was developed and the predicted wind speed is used as an input for a novel feedforward mechanism designed to develop a non-linear relationship between pitch angle and wind speed. Also, they implemented an uncertainty and disturbance estimator (UDE) based feedback controller to build an external disturbance model to deal with it and provide system stability.
Mohamed Abdelkarim et al. proposed a partial offline quasi-min-max fuzzy model-predictive pitch controller considering WT nonlinearities, unstructured model dynamics, pitch angle constraints, and wind speed variations [44]. Fuzzy modeling combined with the MPC algorithm together can achieve optimal system operation by taking into account the pitch angle constraints and WT non-linearities. The quasi-min-max technique incorporated with the fuzzy model guarantees the system’s closed-loop stability by transforming the stability and pitch angle constraints into linear matrix inequality (LMI) problems as it is the optimal tool to solve multi-constrained system problems. In partial offline strategy, offline design is followed by online synthesis, in the offline design, sets of data including pitch angle constraints are computed and the online synthesis includes a simplified optimization problem solved to ensure the stability of the WT closed loop system. Controller validation using FAST simulator showed the effectiveness of the proposed controller over the conventional scheduled PI controller in terms of electrical power, generator speed, and mechanical load reduction, and also reduces the computational burden problem through the partial offline strategy.
H.M. Hassan et al. also proposed an LMI technique to design a robust collective pitch controller (CPC) for large WTs [45]. Due to the uncertainties of the WT model, the controller design constraints have included the H∞ problem for better speed regulation, the H2 problem for optimizing control action with performance, H∞/H2 trade-off criteria to overcome these problems, and also pole clustering to improve transient response by specifying regions representing system’s eigenvalue limits. The CPC controller was first designed based on a single operating point model but it showed drawbacks because it did not meet the designed constraints at all operating points, so a poly-topic model has been considered to overcome these drawbacks by selecting different operating points (six wind speeds). The CPC has been integrated with IPC to cancel the mechanical loads. A performance comparison between the proposed controller and classical collective pitch controller has shown six-fold improvement in speed regulation and a four-fold reduction in fatigue loads but it exerts control effort slightly more than the PI controller, within the permissible limits, which is necessary for mitigating fatigue loads.
Reducing the loading effect on WTs while achieving maximal power output at the same time is an important objective in order to increase the lifetime of the equipment and extract the maximum power. Atif Iqbal et al. designed a fuzzy-based model predictive controller to control pitch angle in region 3 to minimize the load effect and maximize the extracted power [46]. The fuzzy model is designed based on Mamdani’s method by using 49 rules. The MPC has mainly 2 inputs which are rotor speed and output power, while the output variable is feeding to the actuator. The MPC uses output power to predict the system’s behavior. From the simulation and by comparing the proposed method and the conventional PI controller, the proposed controller could reduce the rotor speed and so the mechanical torque as well as extracting maximal power. In comparison to conventional linear controllers, fuzzy controllers provide nonlinear control actions, rely less heavily on mathematical models, and are also better able to reject noise, disturbances, and parameter variations.
Also, for load reduction, Sungsu Park and Yoonsu Nam proposed a separate set of individual and collective pitch control algorithms using a linear–quadratic regulator (LQR) with augmented rotor speed integration (LQRI) to cancel the steady-state error, and the Kalman filter was also designed in order to estimate system states and wind speeds [47]. Although the centralized pitch controller has the advantage of handling multi-control objectives, separate individual and collective pitch controllers are better for controlling rotor speed and bending moments on the blade since the individual pitch controller is considered as secondary controller that acts as on-off mechanism. The proposed pitch controller consists of three control loops: generation torque control, which is kept constant at above-rated speed; collective pitch control that controls rotor speed and improves trade-offs between rotor speed regulation and load reduction; and an individual pitch controller, which is designed as an additional loop around the system to reduce the fluctuating loads on the blades. The simulation showed very good rotor speed regulation and a noticeable reduction in blade bending moments.
Due to the drawbacks of a non-linear MPC (NMPC) based on a conventional structure, which includes complicated implementation and a heavy computational burden, Dongran Song et al. proposed a novel NMPC that uses a discrete prediction model with large time steps, which reduces the number of time discrete points so the solution set becomes numerable and implementation complexity and computational burden are decreased [48]. An iterative algorithm is performed after solution sets are defined from the previewed wind speeds to search the optimal sequence of generator torque and set the first element of it as a controller output. Simulation has been conducted on two models of WT, 1.5 MW and 5 MW wind turbines, and compared with the base controller. The results showed that the proposed NMPC increased the energy extraction efficiency by about 1% for the 1.5 MW WT and 1.28–1.95% for the 5 MW WT.
Controlling each blade’s angle individually is a challenge in variable speed variable pitch wind turbines at the full region, so Mahmood Mirzaei et al. proposed a linear MPC that takes the future values of wind speed measured by LIDAR as a scheduling variable [49]. In order to avoid the complex optimization problem of an MPC, the system has been linearized around an equilibrium point. Two controllers are implemented, the first is a collective pitch controller and the second is an individual pitch controller, which reduces fatigue loads on the blades by adjusting the pitch angle. For the LIDAR uncertainty, the extended Kalman filter algorithm has been used to estimate the effective wind speed on the rotor and then compare it against the filtered information that comes from the LIDAR.
Since the linear model at a specific operating point is not suitable for representing a non-linear WT model leading to plant–model mismatch producing a reference tracking error, which results in errors between the predicted and measured output is a problem that faces predictive controllers. D. Q. Dang et al. proposed an offset predictive controller (OF-PC) for speed control of VSWTs to obtain the zero-offset predictive result by estimating the mismatch between measured and predicted outputs so as to guarantee maximum power [50]. The generator torque can be considered as a control input in order to regulate generator speed to track the optimal speed trajectory, while the rotor speed is the state variable. From simulation and comparison between the proposed and conventional PC controller, in a 240 s simulation, OF-PC showed the highest efficiency of 99.50% with respect to ideal optimal power and also maintained the tip speed ratio at its optimal value which is seven.
Finite control set model predictive control (FCS-MPC) is a discrete model used to predict system behavior for every admissible control set and the one that minimizes the predefined function is finally selected. Dongran Song et al. developed an MPC method by using a finite control set for pitch angle control [51], the wind turbine’s nonlinear model was linearized by a non-standard extended Kalman filter then a discrete-time linear model of the system is used to predict the future value of the state variable for possible control sets. Two quality functions (QF) have been defined to represent the control system’s multi-objectives by making variables follow a reference. The results showed faster action of the pitch actuator and optimal tracking for rotor speed under MPC than under a conventional control system.
Demanded power point tracking (DPPT) control algorithms are integrated into conventional generator torque and blade pitch controllers with a mode switch by Kwansu Kim et al. [52]. Both algorithms use power demanded from higher-level wind farm controllers as reference power to track it. The first algorithm is torque-based control represented as KNU1, it uses two modes switches, one is to turn on DPPT by torque control only when the power demand is lower than the available/measured power and the generator speed is lower than the rated speed. The other mode switch is to turn on the collective pitch controller when the power demand is lower than that measured but the generator speed is higher than the rated speed. The second algorithm is pitch-based control represented by a KNU2 and it uses only one mode switch which turns on and off both DPPT control and collective pitch control at the same time in the cases of region 3 winds. Simulation tests showed that KNU1 has faster control ability but keeps a high tip speed ratio (TSR), which increases the torque coefficient that may increase the wake effect, while KNU2 showed advantages with respect to load.
Another technique that is used today in electric drive system speed control is sliding mode control (SMC), which can provide a fast dynamic response and the ability to deal with the system’s external disturbances and parameter variation while reducing mechanical and drive train loads. The SMC technique switches the desired control action smoothly to attain the preferable performance regarding the system’s parameters and signals. A sliding surface is created to switch the signal smoothly within its limits hence decrease the chattering signals resulting in better system performance [53]. L. Colombo et al. proposed an SMC to regulate rotor speed to its rated speed which corresponds to the rated aerodynamic power of the WT by tracking the rated power [54]. The designed controller considers several uncertainties in the WT model and is based on a unique pitch controller. For controlling speed in region 3, the pitch angle is used as a control input so that the output speed follows the desired speed by considering a pre-defined table containing the aerodynamic power-rated values and the corresponding rated angular speeds. In order to evaluate the proposed controller’s performance, a comparison was made between it and PI control. The absolute tracking error value with respect to rated power has been computed for both controllers and the proposed controller has shown an 11% improvement in reducing the error.
Mehrnoosh and Mohammad Hossein also presented SMC for pitch angle using the PSO-SVM method to calculate its coefficients [55]. However, in [56], a hybrid control algorithm of sliding mode and PI controllers along with an observer which reduces the change in power coefficient parameter errors was proposed. This hybrid algorithm could remove wind speed controller parameters from the designed control algorithm so that the uncertainties and disturbances caused by wind speed change are eliminated. They also discussed the robustness of the proposed algorithm regarding the uncertainties of the WT structure. The simulations declared that the proposed controller algorithm’s root mean square (RMS) error has been improved by 65% compared to the sliding mode control algorithm alone proposed in [55].
Increasing WT size causes interaction between the tower and drive train aerodynamics which results in introducing right half-plane zeros (RHPZ) in the dynamics that link blade pitch angle and generator speed, limiting the control system’s ability to regulate the generator speed through pitch control. So, William E. Leithead and Sergio Dominguez proposed a coordinated controller design (CCD) to overcome this limitation [57]. The controller structure considers one aspect which is the accommodation of aerodynamic non-linearity. The CCD is based on parallel path modification, using both generator and blade pitch, which enables RHPZ to be counteracted and decouple the tower fatigue loads from the generator speed control. In addition, a PI controller is combined in order to achieve the same bandwidth as the conventional controller and make it easily tuned for different WT systems.
Due to WT system uncertainties that cannot be avoided in the mathematical model, the WT’s behavior cannot be exactly presented, meanwhile the pitch control system requires accurate information about the system’s mathematical model or complex equations analysis. Artificial intelligence (AI) control can be a solution for such a problem as it only needs a system’s input and output data without the need for a dynamic model, it only depends on artificial networks which are the computing systems that use the obtained dataset to calculate the considered output. As mentioned before, a PI/PID controller’s gains are difficult to tune precisely in such a complex system like a WT system, so combining artificial intelligence algorithms with a PI/PID controller in order to adjust the controller’s parameters has been proposed in [58][59][60]. Jing Du and Bo Wang implemented a back-propagation neural network (BP-NN) PI controller in order to adjust PI controller parameters through self-learning by the network system [58]. Each neuron in BP neural network has a weight that is adjusted online by taking rated speed, measured speed, and speed difference as inputs to the network system. Simulation analysis using Simpack software was manipulated to compare between PI control with gain-scheduling and a BP neural network PI strategy which showed its improved control effects on maintaining the stability of output power at rated wind speeds since the standard deviation of PI with gain-scheduling was 2.207 while that of a BP neural network PI control was 1.92.
Iman Poultangari et al. also proposed the radial basis function (RBF) neural network to obtain optimal PI gains to construct a CPC [59]. The RBF neural network must be trained with an optimal training dataset to give optimal PI gains. The PSO algorithm was used to obtain the optimal dataset by using some constant speeds above-rated speed to obtain an optimal pair of PI gains for each wind speed value. The constant wind speeds are used as inputs and their corresponding optimal gains as outputs for training the RBF neural network. The proposed method does not need knowledge about the non-linearities and uncertainties of the system. The results showed a favorable performance for the proposed method rather than the conventional PI controller in terms of keeping both generator speed and torque within their rated value with fewer variations and also less usage of pitch actuation.
Wei Jie et al. developed a predictive model for the important parameter variables to control a WT based on analyzing input and output data of wind farms [61]. The model is based on using an extreme learning machine (ELM) algorithm to target the output which reduces the information loss in the transmission process and uses it as reference data for pitch control, which is based on the RBF, while deep LEM (DLEM) has been used to simplify the higher order non-linear mode. The simulation showed a reduction in model computational complexity and computing resource consumption.
Yarong Zou et al. proposed the linear active disturbance rejection control (LADRC)-PI optimization algorithm based on the extremum seeking (ES) algorithm in order to improve disturbance rejection and track the optimal and extreme value working state [62]. The LADRC control design was first evaluated for three different WTs, 50 kW, 275 kW, and 1.5 MW, and they all gave a consistent response. Compared to the traditional PI and PID controllers, the proposed LADRC-ES algorithm showed better setpoint tracking performance and the rise time was reduced to half.
Also, Chengzhen Jia et al. proposed an intelligent adaptive pitch control approach combining feedforward RBF-NN and a finite impulse response (FIR) filter based on LiDAR measurements and LADRC controller variable bandwidth to reduce disturbances and mechanical load, and hence result in system performance enhancement [63]. The hybrid control algorithm can adaptively adjust the control coefficients according to wind speed fluctuations measured 50 m in front of the WT’s blade by a LiDAR sensor. Simulation results showed a remarkable reduction in generator speed fluctuations by 40.8% and blade root load moment by 13.1% compared to a PI controller.
Peng Chen et al. proposed an adaptive dynamic program (ADP) based on reinforcement learning using the system’s data [64]. The ADP can guarantee rotor speed stability around the rated value by controlling/changing pitch angle in the full-load area to indirectly improve the efficiency of wind energy and achieve real-time online learning. The variation in pitch angle to reduce the consumed energy of the pitch actuator is relatively gradual. The controller is based on the Markov decision process (MDP) framework. The simulation results showed better performance than other traditional controllers but it also has some problems which need to be solved by improving the training of neural networks to increase the success rate and speed up learning.
Ahmet Serdar Yilmaz and Zafer Özer have proposed two types of neural networks as pitch angle controllers, multi perceptron with backpropagation (MLP) and RBF [65]. The RBF algorithm was used as a second/alternative controller to MLP. Both neural networks were trained online at variable speeds in a short period of time. MLP-NN has two inputs and one output with five neurons in the hidden layer while RBF-NN has three inputs and one output with 10 neurons in the hidden layer. Both of them have a non-linear activation function in the hidden layer and a linear activation function in the output layer. From the simulation, the RBF-based controller gave better results as it has a smaller settling time.
Different control algorithms were used for the WT pitch control system, considering the system’s nonlinearity. Classical control systems showed simplicity and adaptive response for pitch control, but they showed difficulty in measuring the wind speed precisely while modern and soft computing control techniques showed rapid response and ability to solve the system’s nonlinearity and complexity but also needed rules updating with the change in the system’s parameters variations. Artificial intelligence algorithms have the ability to automatically train and update their variables so they showed a smooth transition between the operating regions, which decreases pitch actuation usage.

This entry is adapted from the peer-reviewed paper 10.3390/en16176394

References

  1. Elliott, D. Assessing the world’s wind resources. IEEE Power Eng. Rev. 2002, 1, 346–347.
  2. Zinmickas, V.; Gecevičius, G.; Markevičius, A. A literature review of wind turbines icing problems. In Proceedings of the CYSENI, International Conference on Energy Issues, Kaunas, Lithuania, 26–27 May 2016.
  3. Global Wind Energy Council. Global Wind Report; Global Wind Energy Council: Brussels, Belgium, 2022.
  4. Kim, H.; Lu, D. Wind energy conversion system from electrical perspective—A survey. Smart Grid Renew. Energy 2010, 1, 119–131.
  5. Hansen, M. Steady BEM Model. In Aerodynamics of Wind Turbines, 2nd ed.; Earthscan: London, UK, 2008.
  6. Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons: Chichester, UK, 2011.
  7. Ekelund, T. Yaw control for reduction of structural dynamic loads in wind turbines. J. Wind Eng. Ind. Aerodyn. 2000, 85, 241–262.
  8. Odgaard, P.; Stoustrup, J.; Kinnaert, M. Fault tolerant control of wind turbines—A benchmark model. IFAC Proc. Vol. 2009, 42, 155–160.
  9. Rivkin, D.; Anderson, L.D.; Silk, L. Wind Turbine Control Systems; Jones & Bartlett Publishers: Burlington, MA, USA, 2012.
  10. Barambones, O.; Cortajarena, J.; Calvo, I.; de Durana, J.G.; Alkorta, P.; Karami-Mollaee, A. Variable speed wind turbine control scheme using a robust wind torque estimation. Renew. Energy 2019, 133, 354–366.
  11. Dube, L.; Garner, G.C.; Garner, K.S.; Kamper, M.J. Simple and robust MPPT current control of a wound rotor synchronous wind generator. Energies 2023, 16, 3290.
  12. Zhao, L.; Xue, L.; Li, Z.; Wang, J.; Yang, Z.; Xue, Y. Progress on offshore wind farm dynamic wake management for energy. J. Mar. Sci. Eng. 2022, 10, 1395.
  13. Shah, K.; Meng, F.; Li, Y.; Nagamune, R.; Zhou, Y.; Ren, Z.; Jiang, Z. A synthesis of feasible control methods for floating offshore wind turbine system dynamics. Renew. Sustain. Energy Rev. 2021, 151, 111525.
  14. Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 2021, 304, 117766.
  15. Ha, K.; Truong, H.; Dang, T.; Ahn, K. Recent Control technologies for floating offshore wind energy system: A review. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 8, 281–301.
  16. Choi, H.; Kim, J.; Cho, J.; Nam, Y. Active yaw control of MW class wind turbine. In Proceedings of the International Conference on Control, Automation and Systems, Gyeonggi-do, Republic of Korea, 27–30 October 2010.
  17. Sheng, S. Report on Wind Turbine Subsystem Reliability—A Survey of Various Databases; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2013.
  18. Garcia-Sanz, M.; Houpis, C. Wind Energy Systems: Control Engineering Design; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2012.
  19. Muljadi, E.; Butterfield, C.P. Pitch-controlled variable-speed wind turbine generation. IEEE Trans. Ind. Appl. 2001, 37, 240–246.
  20. Karthik, R.; Hari, A.S.; Kumar, Y.V.P.; Pradeep, D.J. Modelling and control design for variable speed wind turbine energy system. In Proceedings of the International Conference on Artificial Intelligence and Signal Processing (AISP), Amaravati, India, 10–12 January 2020.
  21. Jauch, C.; Islam, S.M.; Sørensen, P.; Jensen, B.B. Design of a wind turbine pitch angle controller for power system stabilisation. Renew. Energy 2007, 32, 2334–2349.
  22. Gao, R.; Gao, Z. Pitch control for wind turbine systems using optimization, estimation and compensation. Renew. Energy 2016, 91, 501–515.
  23. Iqbal, A.; Ying, D.; Saleem, A.; Hayat, M.A.; Mateen, M. Proposed particle swarm optimization technique for the wind turbine control system. Meas. Control 2020, 53, 1022–1030.
  24. Goyal, S.; Deolia, V.K.; Agrawal, S. An advanced neuro-fuzzy tuned PID controller for pitch control of horizontal axis wind turbines. ECTI Trans. Electr. Eng. Electron. Commun. 2022, 20, 296305.
  25. Jiang, S.-J.; Chu, S.-C.; Zou, F.-M.; Shan, J.; Zheng, S.-G.; Pan, J.-S. A parallel Archimedes optimization algorithm based on Taguchi method for application in the control of variable pitch wind turbine. Math. Comput. Simul. 2022, 203, 306–327.
  26. Shan, J.; Chu, S.-C.; Weng, S.-W.; Pan, J.-S.; Jiang, S.-J.; Zheng, S.-G. A parallel compact firefly algorithm for the control of variable pitch wind turbine. Eng. Appl. Artif. Intell. 2022, 111, 104787.
  27. Sule, A.H.; Mokhtar, A.S.B.; Jamian, J.J.B. Optimal PI pitch control of SCIG wind turbine using Grey Wolf Optimizer for dynamic stability. Nov. Perspect. Eng. Res. 2022, 7, 45–68.
  28. Kumar, D.; Chatterjee, K. A review of conventional and advanced MPPT algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2016, 55, 957–970.
  29. Van, T.L.; Nguyen, T.H.; Lee, D.-C. Advanced pitch angle control based on fuzzy logic for variable-speed wind turbine systems. IEEE Trans. Energy Convers. 2015, 30, 578–587.
  30. Prats, M.; Carrasco, J.; Galvan, E.; Sanchez, J.; Franquelo, L. Improving transition between power optimization and power limitation of variable speed, variable pitch wind turbines using fuzzy control techniques. In IEEE International Conference on Industrial Electronics, Control and Instrumentation, 21st Century Technologies, Proceedings of the 2000 26th Annual Conference of the IEEE Industrial Electronics Society (IECON 2000), Nagoya, Japan, 22–28 October 2000; IEEE: New York, NY, USA, 2000.
  31. Scherillo, F.; Izzo, L.; Coiro, D.; Lauria, D. Fuzzy logic control for a small pitch-controlled wind turbine. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012.
  32. Civelek, Z. Optimization of fuzzy logic (Takagi-Sugeno) blade pitch angle controller in wind turbines by genetic algorithm. Eng. Sci. Technol. Int. J. 2020, 23, 1–9.
  33. Duong, M.; Grimaccia, F.; Leva, S.; Mussetta, M. Pitch angle control using hybrid controller for all operating regions of SCIG wind turbine system. Renew. Energy 2014, 70, 197–203.
  34. Pan, L.; Wang, X. Variable pitch control on direct-driven PMSG for offshore wind turbine using Repetitive-TS fuzzy PID control. Renew. Energy 2020, 159, 221–237.
  35. Sahoo, S.; Panda, G. Control and comparison of power for a variable-speed wind turbine using fuzzy PID controller. In Advanced Computational Paradigms and Hybrid Intelligent Computing; Advances in Intelligent Systems and Computing; Springer: Singapore, 2022; Volume 1373, pp. 385–393.
  36. Rashid, A.; Ying, D. Study on the variable pitch control of the wind power unit based on mamdani inference and conventional control algorithm. IOP Conf. Ser. Earth Environ. Sci. 2020, 529, 012005.
  37. Golnary, F.; Tse, K. Novel sensorless fault-tolerant pitch control of a horizontal axis wind turbine with a new hybrid approach for effective wind velocity estimation. Renew. Energy 2021, 179, 1291–1315.
  38. Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium, Arlington, TX, USA, 26–28 September 2010.
  39. Petrovic, V.; Jelavic, M.; Baotic, M. MPC framework for constrained wind turbine individual pitch control. Wind Energy 2021, 24, 54–68.
  40. Lasheen, A.; Elshafei, A. Wind-turbine collective-pitch control via a fuzzy predictive algorithm. Renew. Energy 2016, 87, 298–306.
  41. Fahmy, Y.; El-Badawy, A. Fuzzy model predictive pitch control of flexible wind turbine blade. In Advances in Nonlinear Dynamics; NODYCON Conference Proceedings Series; Springer: Cham, Switzerland, 2022; pp. 49–60.
  42. Venkaiah, P.; Sarkar, B.K. Hydraulically actuated horizontal axis wind turbine pitch control by model free adaptive controller. Renew. Energy 2020, 147, 55–68.
  43. Jiao, X.; Yang, Q.; Xu, B. Hybrid intelligent feedforward-feedback pitch control for VSWT with predicted wind speed. IEEE Trans. Energy Convers. 2021, 36, 2770–2781.
  44. Abdelbaky, M.; Liu, X.; Jiang, D. Design and implementation of partial offline fuzzy model-predictive pitch controller for large-scale wind-turbines. Renew. Energy 2020, 145, 981–996.
  45. Hassan, H.; ElShafei, A.; Farag, W.; Saad, M. A robust LMI-based pitch controller for large wind turbines. Renew. Energy 2012, 44, 63–71.
  46. AIqbal; Ying, D.; Saleem, A.; Hayat, M.; Mehmood, K. Efficacious pitch angle control of variable-speed wind turbine using fuzzy based predictive controller. In Proceedings of the 6th International Conference on Power and Energy Systems Engineering (CPESE 2019), Okinawa, Japan, 20–23 September 2019.
  47. Park, S.; Nam, Y. Two LQRI based blade pitch controls for wind turbines. Energies 2012, 5, 1998–2016.
  48. Songa, D.; Yang, Y.; Zheng, S.; Deng, X.; Su, M.; Tang, W.; Yang, X.; Huang, L.; Joo, Y.H. New perspectives on maximum wind energy extraction of variable-speed wind turbines using previewed wind speeds. Energy Convers. Manag. 2020, 206, 112496.
  49. Mirzaei, M.; Soltani, M.; Poulsen, N.K.; Niemann, H.H. An MPC approach to individual pitch control of wind turbines using uncertain LIDAR measurements. In Proceedings of the European Control Conference (ECC), Zürich, Switzerland, 17–19 July 2013.
  50. Dang, D.Q.; Wang, Y.; Cai, W. Offset-Free Predictive Control for Variable Speed Wind Turbines. IEEE Trans. Sustain. Energy 2012, 4, 2–10.
  51. Song, D.; Yang, J.; Dong, M.; Joo, Y.H. Model predictive control with finite control set for variable-speed wind turbines. Energy 2017, 126, 564–572.
  52. Kim, K.; Kim, H.-G.; Cheol-jin, K.; Paek, I.; Bottasso, C.L.; Campagnolo, F. Design and validation of demanded power point tracking control algorithm of wind turbine. Int. J. Precis. Eng. Manuf.-Green Technol. 2018, 5, 387–400.
  53. Menezes, E.; Araújo, A.; Silva, N. A review on wind turbine control and its associated methods. J. Clean. Prod. 2018, 174, 945–953.
  54. Colombo, L.; Corradini, M.; Ippoliti, G.; Orlando, G. Pitch angle control of a wind turbine operating above the rated wind speed: A sliding mode control approach. ISA Trans. 2019, 96, 95–102.
  55. Kamarzarrin, M.; Refan, M.H. Intelligent sliding mode adaptive controller design for wind turbine pitch control system using PSO-SVM in presence of disturbance. J. Control Autom. Electr. Syst. 2020, 31, 912–925.
  56. Jajarm, A.E.; Dideban, A.; Ozgoli, S. A new sliding mode controller for wind turbine pitch angle. Asian J. Control 2022, 25, 2214–2228.
  57. Leithead, W.E.; Dominguez, S. Coordinated control design for wind turbine control systems. In Proceedings of the European Wind Energy Conference and Exhibition, Athens, Greece, 27 February–2 March 2006.
  58. Du, J.; Wang, B. Pitch control of wind turbines based on BP neural network PI. J. Phys. Conf. Ser. 2020, 1678, 012060.
  59. Poultangari, I.; Shahnazi, R.; Sheikhan, M. RBF neural network based PI pitch controller for a class of 5-MW wind turbines using particle swarm optimization algorithm. ISA Trans. 2012, 51, 641–648.
  60. Ren, H.; Hou, B.; Zhou, G.; Shen, L.; WeI, C.; Li, Q. Variable pitch active disturbance rejection control of wind turbines based on BP Neural network PID. IEEE Access 2020, 8, 71782–71797.
  61. Jie, W.; Chu, J.; Lin, Y.; Wenliang, W.; Jian, D. Pitch control of wind turbine based on deep neural network. In Proceedings of the International Conference on New Energy and Sustainable Development, Changchun, China, 21–23 August 2020.
  62. Zou, Y.; Tan, W.; Jin, X.; Jin, X. An active disturbance rejection control of large wind turbine pitch angle based on extremum-seeking algorithm. Energies 2022, 15, 2846.
  63. Jia, C.; Wang, L.; Meng, E.; Chen, L.; Liu, Y.; Jia, W.; Bao, Y.; Bao, Y. Combining LIDAR and LADRC for intelligent pitch control of wind turbines. Renew. Energy 2021, 169, 1091–1105.
  64. Chen, P.; Han, D.; Tan, F.; Wang, J. Reinforcement-based robust variable pitch control of wind turbines. IEEE Access 2020, 8, 20493–20502.
  65. Yilmaz, A.S.; Özer, Z. Pitch angle control in wind turbines above the rated wind speed by multi-layer perceptron and radial basis function neural networks. Expert Syst. Appl. 2009, 36, 9767–9775.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback