Spiking Neural Networks and Neuromorphic Modeling: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Martin Do Pham
,
Amedeo D’Angiulli
,
Maryam Mehri Dehnavi
,
Robin Chhabra

Use of Spiking Neural Networks (SNNs) that can capture a model of organisms’ nervous systems, may be simply justified by their unparalleled energy/computational efficiency.

  • neuromorphics
  • spiking neural networks
  • embodied cognition

1. Introduction

Understanding how living organisms function within their surrounding environment reveals the key properties essential to designing and operating next-generation intelligent systems. A central actor enabling organisms’ complex behavioral interactions with the environment is indeed their efficient information processing through neuronal circuitries. Although biological neurons transfer information in the form of trains of impulses or spikes, Artificial Neural Networks (ANNs) that are mostly employed in the current Artificial Intelligence (AI) practices do not necessarily admit a binary behavior. In addition to the obvious scientific curiosity of studying intelligent living organisms, the interest in the biologically plausible neuronal models, i.e., Spiking Neural Networks (SNNs) that can capture a model of organisms’ nervous systems, may be simply justified by their unparalleled energy/computational efficiency.
Inspired by the spike-based activity of biological neuronal circuitries, several neuromorphic chips, such as Intel’s Loihi chip [1], have been emerging. These pieces of hardware process information through distributed spiking activities across analog neurons, which, to some extent, trivially assume biological plausibility; hence, they can inherently leverage neuroscientific advancements in understanding neuronal dynamics to improve the computational solutions for, e.g., robotics and AI applications. Due to their unique processing characteristics, neuromorphic chips fundamentally differ from traditional von Neumann computing machines, where a large energy/time cost is incurred whenever data must be moved from memory to processor and vice versa. On the other hand, coordinating parallel and asynchronous activities of a massive SNN on a neuromorphic chip to perform an algorithm, such as a real-time AI task, is non-trivial and requires new developments of software, compilers, and simulations of dynamical systems. The main advantages of such hardware are (i) computing architectures organized closely to known biological counterparts may offer energy efficiency, (ii) well-known theories in cognitive science can be leveraged to define high-level cognition for artificial systems, and (iii) robotic systems equipped with neuromorphic technologies can establish an empirical testbench to contribute to the research on embodied cognition and to explainability of SNNs. Particularly, this arranged marriage between biological plausibility and computational efficiency perceived from studying embodied human cognition has greatly influenced the field of AI.

2. SNNs and Neuromorphic Modeling

Note that the category of bio-inspired computing is an unsettled one, and it is unclear how such systems can be designed to integrate into existing computing architectures and solutions [2]. Consider the neuron as the basic computational element of a SNN [3]. Figure 1 shows a simplified biological neuron consisting of dendrites where post-synaptic interactions with other neurons occur, a soma where an action potential (i.e., a spike in cell membrane voltage potential) is generated, and an axon with a terminal where an action potential is triggered for pre-synaptic interactions.
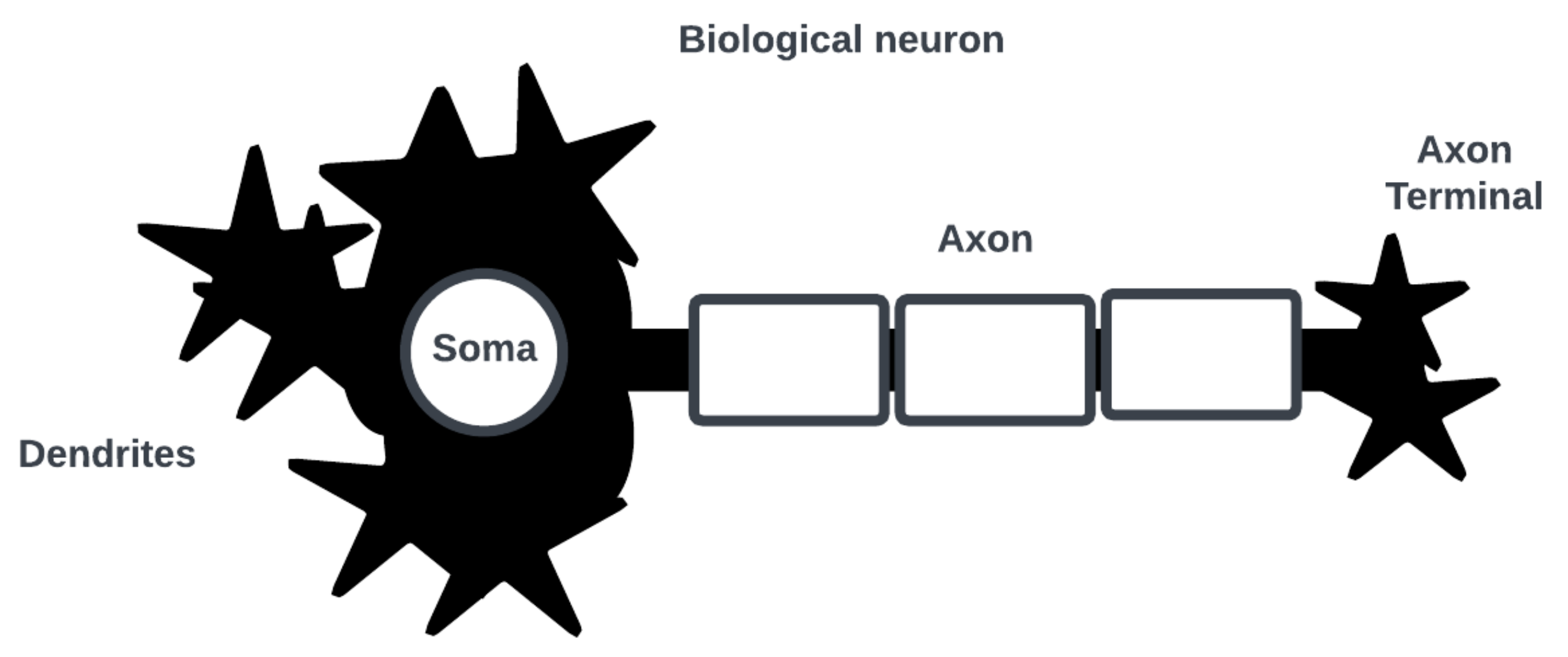
Brainsci 13 01316 g001
Figure 1. Simplified diagram of biological neuron and its main parts of interest.
One way to model a spiking neuron is using compartmental models [4] that consider each of these morphological components separately, with their own sets of dynamical equations coupled together to represent the functional anatomy of a neuronal cell [5]. For example, as in Figure 2, the equations describing the membrane potential associated with the dendrites are only coupled to the soma but the equations associated with the soma are coupled to the axon as well. Thus, interactions at the subcellular level are modeled locally to represent cell anatomy.
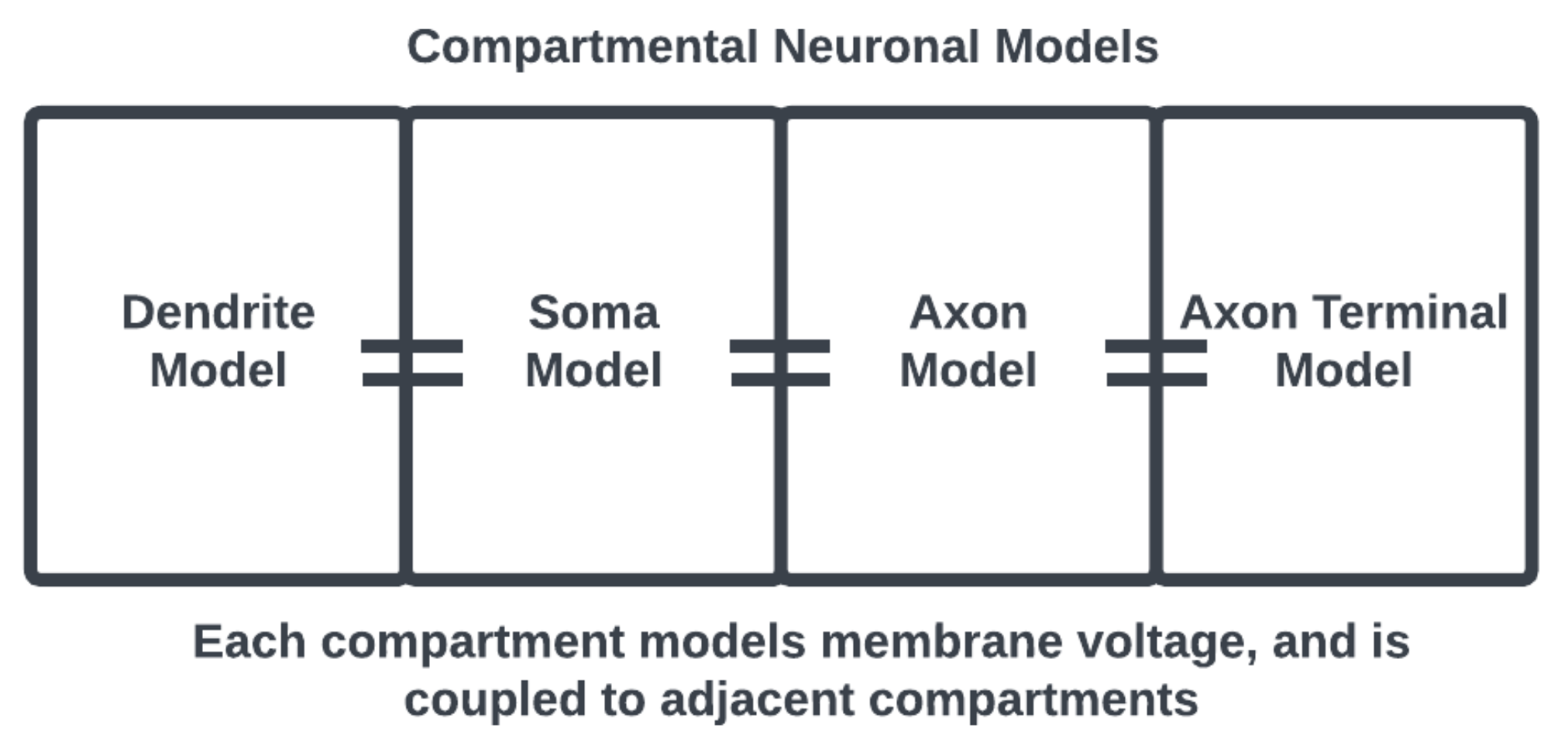
Brainsci 13 01316 g002
Figure 2. Compartmental neuronal model, the adjacency of compartments considers the physical structure of a neuron. Compartments may also be prescribed with appropriate subcellular morphology.
The advantage of this model is the structural details and subcellular local effects that may be included; however, the model of a neural network becomes too complex and difficult to compute. In this sense, compartmental models may be viewed as biologically plausible but computationally unfeasible for many applications beyond investigations at the cellular level. The work of [6] implemented a multi-compartmental model on the SpiNNaker neuromorphic hardware to incorporate dendritic processing into the model of computation.
On the other hand, most neuromorphic hardware implements a simplified form of neuronal models, known as a pointwise model (see Figure 3), where a neuron is conceptualized as a single point. Pointwise models abstract the intracellular dynamics into a state voltage variable that records a spike when the voltage exceeds a threshold to effectively capture the action potential behavior of the neuron without having to model its structure. Therefore, unlike compartmental neuronal models that capture the spatiotemporal neuronal dynamics allowing for electrochemical process simulations, pointwise models offer computationally efficient simulations for large-scale networks neglecting spatial complexity.
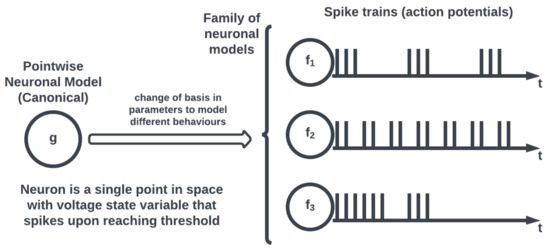
Brainsci 13 01316 g003
Figure 3. Pointwise neuronal models and canonical equations.
The difference between compartmental and pointwise neuronal models is just one design decision when simulating neural systems, and it can be argued that the latter lacks biological plausibility. A now near-canonical example of neuronal modeling is the Hodgkin–Huxley model describing the dynamics of action potentials in neurons [7]. In the case of Hodgkin–Huxley, a continuous-time system of differential equations forming a mathematical template for neuronal modeling was derived by selecting squid as a biological specimen and analyzing its nervous system. Despite its descriptive completeness and prescriptive accuracy, this formalization is still an abstraction suffering from the representation problem of the map-territory relation [8]. Furthermore, the required computational machinery to implement the simulation of a single neuron based on the Hodgkin–Huxley model outweighs its biological completeness [9]. Generally, it is undeniable that the computational feasibility of any model inherently comes at the cost of some inevitable reduction in biological veridicality. Following Hodgkin–Huxley’s seminal work, much development has been made in capturing the dynamics of neuronal cells. The work of Izhikevich [10] showed that many observed spiking patterns could be reproduced using a small set of differential equations and that these equations were also simpler to compute while making a tradeoff in physically meaningful quantities. The eponymously named model consists of a pair of first-order differential equations on the space of the membrane potential and recovery variable of a neuron along with a simple spiking thresholding logic. Related works named these equations the canonical model approach, where the variability of spiking behaviors could be accounted for using a change of basis in the variables of the dynamical equations [11]. Accordingly, a neuronal model can be re-written in the form of the canonical system which allows for a consolidation of neuronal activity analysis under one dynamical system. The advantage of this approach is that an empirically observed spiking behavior may be modeled by a complicated and biologically detailed model or a simplified and reduced form, depending on needs and resources. The canonical approach also allows for the investigation of different kinds of spiking behavior (bursting, phasic) generated by the same neuronal dynamics under different parameter regimes, which is a step towards the standardization of neuronal models matching observed empirical data. Under this approach, dynamical systems theory bears upon the neurophysiological understanding via simulating the (biological) spiking behavior of different types of neuronal cells employing the appropriate canonical model with specific parameterizations [12]. The problem of modeling neurons’ spiking behavior then transforms into selecting the differential equation and estimating its parameters. It is from this formalized neuronal dynamics position that the GNC of neurorobotic systems is revisited in a later section. A discussion and summary table of biological plausibility and computational efficiency for different neuronal models, including Hodgkin–Huxley, Izhikevich, and integrate-and-fire, are documented in [9].
Canonical models are advantageous in studying the behavior of a single spiking neuron because they standardize the mechanisms of action potentials using the mathematical theory of dynamical systems. Together, populations of homogenous or heterogenous neurons may be connected to form a SNN and simulate its time evolution of neural activity. The resulting neural network fundamentally differs from an ANN where the input/output information and its process are not embedded in a temporal dimension. It is still an open problem how the information is encoded in a spike train, whether the frequency of spikes in a time window encodes information (rate-based) or the time between the spikes (spike-based). Brette suggests that rate-based encoding is a useful but limited ad-hoc heuristic for understanding neural activities and that spike-based encoding is more supported both empirically and theoretically [13]. For example, there are studies supporting interspike interval (a spike-based method) information encoding in the primary visual cortex [14].
The topology of a SNN prescribes how the neuronal activities are connected to each other by weights representing synaptic modulation between neurons (see Figure 4). The work of [15] showed that there are highly non-random small patterns of connectivity in cortical networks, an idea expanded upon more broadly for the brain by [16]. These non-random patterns between neurons are called motifs [17], an example of which is a typical convolutional (non-recurrent, feedforward) organization (Figure 5). Organizing sets of motifs, layers or populations of coordinated neural activities may be constructed (Figure 6). The connectivity pattern and structure of the network influence information flow, signal processing, and the emergence of network dynamics. The choice of topology impacts how neurons communicate and interact with each other, affecting the propagation of spiking activity, synchronization, and formation of functional circuits. Different topologies, such as feedforward, recurrent, or hierarchical structures, offer unique computational capabilities. For example, feedforward networks excel at information propagation and feature extraction, while recurrent networks enable memory and feedback mechanisms. The topology of a SNN is a fundamental design parameter that shapes its computational properties and determines its ability to perform specific tasks, making it a key consideration in designing and understanding neuronal computation.
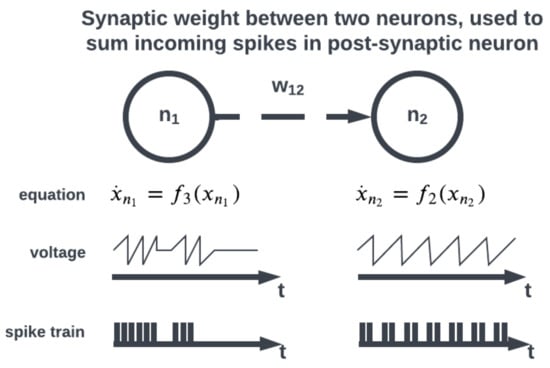
Brainsci 13 01316 g004
Figure 4. Incoming spikes between neurons are summed using a synaptic weight.
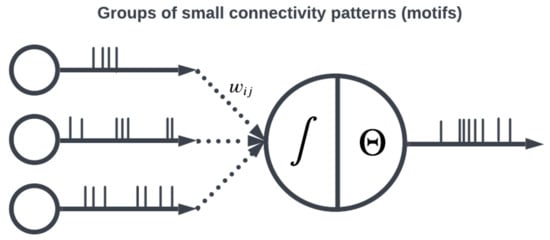
Brainsci 13 01316 g005
Figure 5. Patterns of connectivity are determined by weights between neurons.
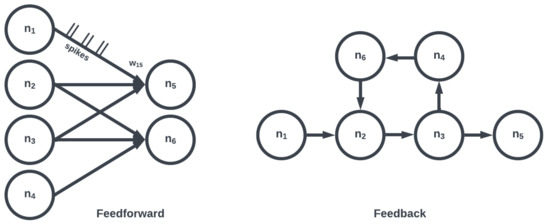
Brainsci 13 01316 g006
Figure 6. Large collections of motifs form layers or populations (e.g., convolutional, recurrent). Two networks consisting of the same number of neurons and edges may differ depending on organization.
Large organizations of coordinated neural populations may be trained to perform AI tasks or approximate functions [18] (see Figure 7). In addition to the SNN topology, the adaptation rule that specifies the weights between interconnected neurons plays a crucial role in determining the computation performed by the network. Here, Hebb’s postulates, what are aphoristically understood as “cells that fire together wire together” [19], remains the dominant neuroscientific insight for learning. A seminal work in modeling synaptic plasticity, this is a well-known unsupervised learning technique called Spike-Timing-Dependent Plasticity (STDP) [20]. The STDP method works based on the selection of a learning window (see Figure 8) describing the asymmetric modification of the synaptic conductance between two neurons: when the presynaptic neuron fires before (after) the postsynaptic neuron, the conductance is strengthened (attenuated). The smaller the time interval between spikes, the greater the magnitude of modification in either direction. By applying a learning algorithm such as STDP to a population of spiking neurons, the learned (conductance) connection weights between neurons capture the topology of the network. A historical account of the developments from Hebb’s synaptic plasticity postulate to the STDP learning rule and its modern variations can be found in [21]. A survey of methods for learning via SNNs in [22] reveals that most learning models are STDP-based [23].
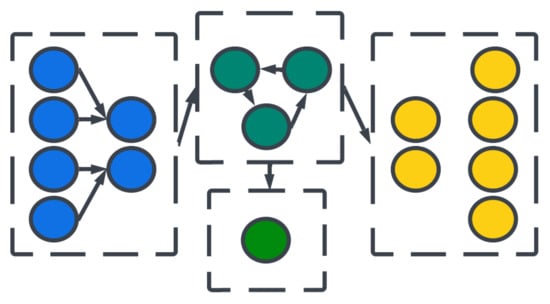
Brainsci 13 01316 g007
Figure 7. Organizations of neural layers and populations form architectures.
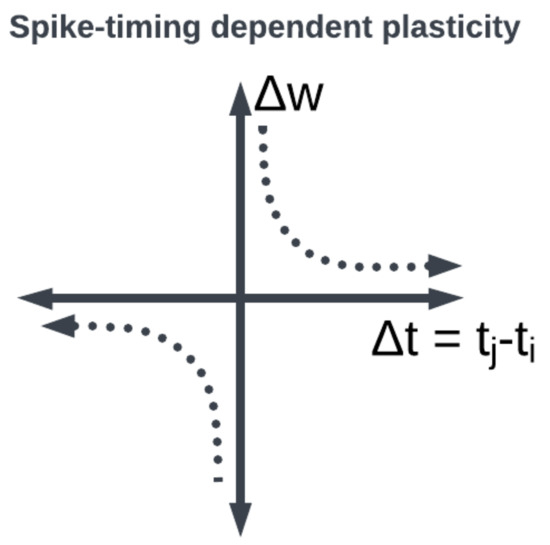
Brainsci 13 01316 g008
Figure 8. STDP synaptic learning rule window function: the weight between neurons is modified depending on when the pre- and post-synaptic neurons fired.
Alternative methods exist to learn synaptic weights, and their development is an active area of research for applications where biological fidelity may not be a priority. One such method is to convert ANNs to SNNs by mapping their weights [24][25][26]. Another approach is to use surrogate-gradient descent [27] such that traditional deep learning methods may be used by choosing an appropriate substitute for the spiking neurons’ Heaviside activation function. The substitute is typically a function that approximates the Heaviside function but has smooth gradients, such as the tangent hyperbolic function.

This entry is adapted from the peer-reviewed paper 10.3390/brainsci13091316

References

  1. Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99.
  2. Mehonic, A.; Kenyon, A.J. Brain-inspired computing needs a master plan. Nature 2022, 604, 255–260.
  3. Yuste, R. From the neuron doctrine to neural networks. Nat. Rev. Neurosci. 2015, 16, 487–497.
  4. Yuste, R.; Tank, D.W. Dendritic integration in mammalian neurons, a century after Cajal. Neuron 1996, 16, 701–716.
  5. Ferrante, M.; Migliore, M.; Ascoli, G.A. Functional impact of dendritic branch-point morphology. J. Neurosci. 2013, 33, 2156–2165.
  6. Ward, M.; Rhodes, O. Beyond LIF Neurons on Neuromorphic Hardware. Front. Neurosci. 2022, 16, 881598.
  7. Bishop, J.M. Chapter 2: History and Philosophy of Neural Networks. In Computational Intelligence; Eolss Publishers: Paris, France, 2015.
  8. Bateson, G. Steps to an Ecology of Mind: Collected Essays in Anthropology, Psychiatry, Evolution, and Epistemology; University of Chicago Press: Chicago, IL, USA, 1972.
  9. Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070.
  10. Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572.
  11. Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; MIT Press: Cambridge, MA, USA, 2007; p. 441.
  12. Hoppensteadt, F.C.; Izhikevich, E. Canonical neural models. In Brain Theory and Neural Networks; The MIT Press: Cambridge, MA, USA, 2001.
  13. Brette, R. Philosophy of the spike: Rate-based vs. spike-based theories of the brain. Front. Syst. Neurosci. 2015, 9, 151.
  14. Reich, D.S.; Mechler, F.; Purpura, K.P.; Victor, J.D. Interspike Intervals, Receptive Fields, and Information Encoding in Primary Visual Cortex. J. Neurosci. 2000, 20, 1964–1974.
  15. Song, S.; Sjöström, P.J.; Reigl, M.; Nelson, S.; Chklovskii, D.B. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 2005, 3, e68.
  16. Sporns, O. The non-random brain: Efficiency, economy, and complex dynamics. Front. Comput. Neurosci. 2011, 5, 5.
  17. Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network motifs: Simple building blocks of complex networks. Science 2002, 298, 824–827.
  18. Suárez, L.E.; Richards, B.A.; Lajoie, G.; Misic, B. Learning function from structure in neuromorphic networks. Nat. Mach. Intell. 2021, 3, 771–786.
  19. Hebb, D. The Organization of Behavior: A Neuropsychological Theory, 1st ed.; Psychology Press: London, UK, 1949.
  20. Song, S.; Miller, K.D.; Abbott, L.F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 2000, 3, 919–926.
  21. Markram, H.; Gerstner, W.; Sjöström, P.J. A history of spike-timing-dependent plasticity. Front. Synaptic Neurosci. 2011, 3, 4.
  22. Gavrilov, A.V.; Panchenko, K.O. Methods of learning for spiking neural networks. A survey. In Proceedings of the 2016 13th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, Russia, 3–6 October 2016; IEEE: Piscataway, NJ, USA, 2016; Volume 2, pp. 455–460.
  23. Taherkhani, A.; Belatreche, A.; Li, Y.; Cosma, G.; Maguire, L.P.; McGinnity, T.M. A review of learning in biologically plausible spiking neural networks. Neural Netw. 2020, 122, 253–272.
  24. Midya, R.; Wang, Z.; Asapu, S.; Joshi, S.; Li, Y.; Zhuo, Y.; Song, W.; Jiang, H.; Upadhay, N.; Rao, M.; et al. Artificial neural network (ANN) to spiking neural network (SNN) converters based on diffusive memristors. Adv. Electron. Mater. 2019, 5, 1900060.
  25. Rueckauer, B.; Liu, S.C. Conversion of analog to spiking neural networks using sparse temporal coding. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5.
  26. Shrestha, S.B.; Orchard, G. Slayer: Spike layer error reassignment in time. arXiv 2018, arXiv:1810.08646.
  27. Neftci, E.O.; Mostafa, H.; Zenke, F. Surrogate gradient learning in spiking neural networks: Bringing the power of gradient-based optimization to spiking neural networks. IEEE Signal Process. Mag. 2019, 36, 51–63.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback