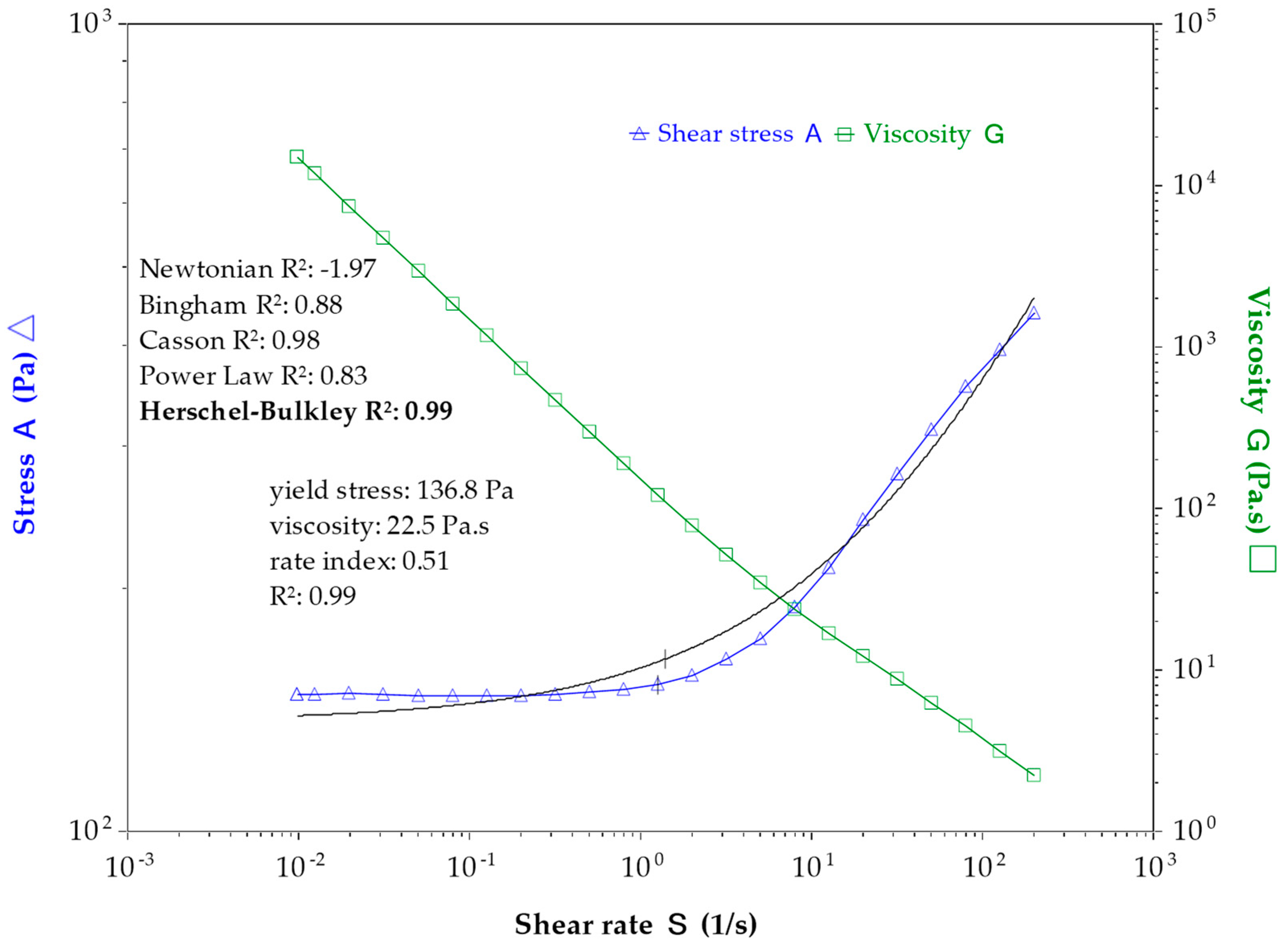
The rheological behavior of cement paste displays several complexities such as non-linearity, yielding, time-dependence and chemical changes. The most common testing procedures allowing for the characterization of this behavior have been reported. For flow behavior, the most relevant protocol consists of the application of a ramp sweep (shear rate or shear stress) so that the flow curve (shear stress as a function of the shear rate) is at steady state flow. The structural build-up can be characterized by static yield stress measurements or the SAOS protocol for various resting times. The non-linearity of flow behavior corresponds to a shear-thinning/shear-thickening phenomenon that can be represented by the Herschel–Bulkley model. If the shear-thinning phenomenon can be related to the flocculation state, the origins of shear thickening are not clearly elucidated. Theories based on order–disorder transition, particle clustering, or viscous/inertial regime transition have been developed to explain the appearance of shear thickening.
- cement paste
- rheology
- yield stress
1. Introduction
2. Testing Procedures
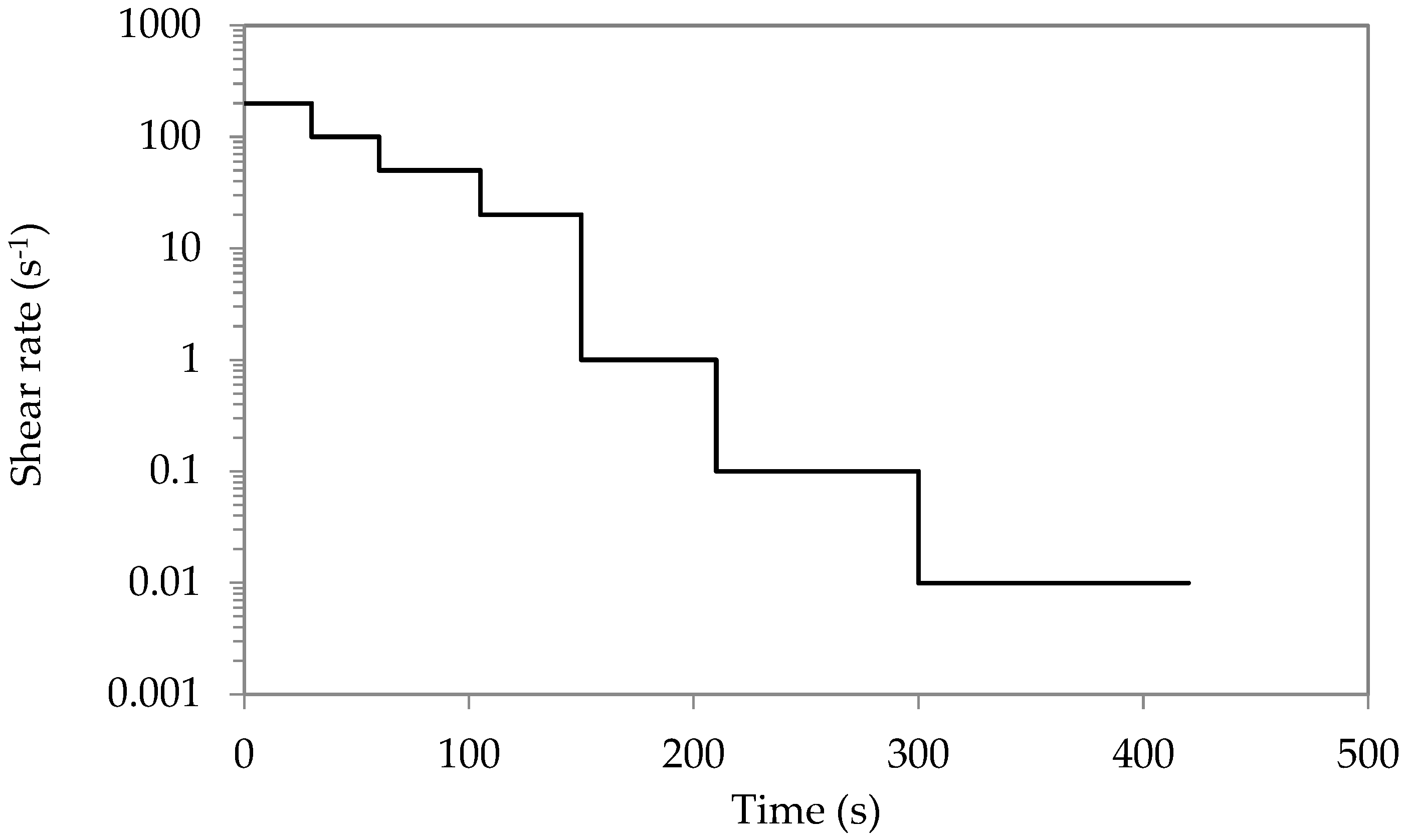
2.1. Flow Tests
2.2. Oscillation Metods
2.3. Transient Mode
3. Rheological Behavior of Cement Paste
3.1. Flow Behavior
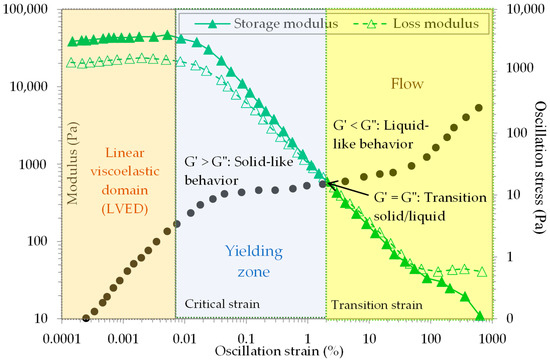
3.2. Linear Visco-Elastic Domain
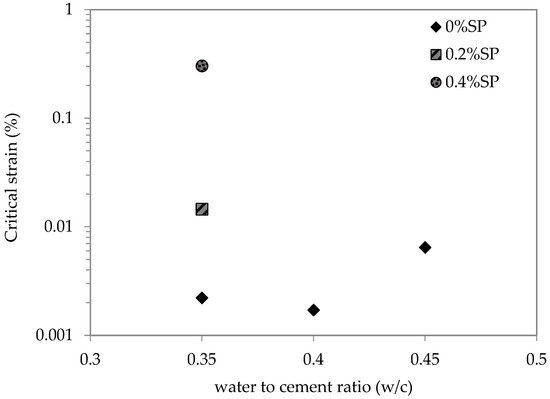
3.3. Structural Build-Up
4. Conclusions
This entry is adapted from the peer-reviewed paper 10.3390/eng4030107
References
- Nicolas, R.; Richard, B.; Nicolas, D.; Irina, I.; Temitope, K.J.; Dirk, L.; Viktor, M.; Romain, M.; Arnaud, P.; Ursula, P.; et al. Assessing the fresh properties of printable cement-based materials: High potential tests for quality control. Cem. Concr. Res. 2022, 158, 106836.
- Biricik, Ö.; Mardani, A. Parameters affecting thixotropic behavior of self compacting concrete and 3D printable concrete; a state-of-the-art review. Constr. Build. Mater. 2022, 339, 127688.
- Roussel, N. Rheological requirements for printable concretes. Cem. Concr. Res. 2018, 112, 76–85.
- Li, R.; Lei, L.; Plank, J. Influence of PCE superplasticizers on the fresh properties of low carbon cements containing calcined clays: A comparative study of calcined clays from three different sources. Cem. Concr. Compos. 2023, 139, 105072.
- Ayati, B.; Newport, D.; Wong, H.; Cheeseman, C. Low-carbon cements: Potential for low-grade calcined clays to form supplementary cementitious materials. Clean. Mater. 2022, 5, 100099.
- Gaimster, R.; Dixon, N. Self-compacting concrete. In Advanced Concrete Technology; Japan Concrete Institute: Tokyo, Japan, 2003; pp. 1–23.
- Brouwers, H.J.H.; Radix, H.J. Self-compacting concrete: Theoretical and experimental study. Cem. Concr. Res. 2005, 35, 2116–2136.
- Wu, H.; Hu, R.; Yang, D.; Ma, Z. Micro-macro characterizations of mortar containing construction waste fines as replacement of cement and sand: A comparative study. Constr. Build. Mater. 2023, 383, 131328.
- Duan, Z.; Deng, Q.; Liang, C.; Ma, Z.; Wu, H. Upcycling of recycled plastic fiber for sustainable cementitious composites: A critical review and new perspective. Cem. Concr. Compos. 2023, 142, 105192.
- Roussel, N.; Bessaies-Bey, H.; Kawashima, S.; Marchon, D.; Vasilic, K.; Wolfs, R. Recent advances on yield stress and elasticity of fresh cement-based materials. Cem. Concr. Res. 2019, 124, 105798.
- Roussel, N.; Lemaître, A.; Flatt, R.J.; Coussot, P. Steady state flow of cement suspensions: A micromechanical state of the art. Cem. Concr. Res. 2010, 40, 77–84.
- Hsu, K.C.; Chiu, J.J.; Da Chen, S.; Tseng, Y.C. Effect of addition time of a superplasticizer on cement adsorption and on concrete workability. Cem. Concr. Compos. 1999, 21, 425–430.
- Chiocchio, G.; Paolini, A.E. Optimum time for adding superplasticizer to Portland cement pastes. Cem. Concr. Res. 1985, 15, 901–908.
- Houst, Y.F.; Flatt, R.J.; Bowen, P.; Hofmann, H.; Mäder, U.; Widmer, J.; Sulser, U.; Bürge, T.A. Influence of Superplasticizer Adsorption on the Rheology of Cement Paste. In Proceedings of the International RILEM Conference on “The Role of Admixtures in High Performance Concrete”, Monterrey, Mexico, 21–26 March 1999; pp. 387–402.
- Cyr, M.; Legrand, C.; Mouret, M. Study of the shear thickening effect of superplasticizers on the rheological behaviour of cement pastes containing or not mineral additives. Cem. Concr. Res. 2000, 30, 1477–1483.
- Khayat, K.H.; Yahia, A.; Sayed, M. Effect of supplementary cementitious materials on rheological properties, bleeding, and strength of structural grout. ACI Mater. J. 2008, 105, 585–593.
- Jiao, D.; De Schutter, G. Insights into the viscoelastic properties of cement paste based on SAOS technique. Constr. Build. Mater. 2022, 357, 129320.
- Legrand, C. Contribution à l’étude de la rhéologie du béton frais. Matér. Constr. 1972, 5, 379–393.
- Yuan, Q.; Zhou, D.; Khayat, K.H.; Feys, D.; Shi, C. On the measurement of evolution of structural build-up of cement paste with time by static yield stress test vs. small amplitude oscillatory shear test. Cem. Concr. Res. 2017, 99, 183–189.
- El Bitouri, Y.; Azéma, N. On the “Thixotropic” Behavior of Fresh Cement Pastes. Eng 2022, 3, 677–692.
- Mostafa, A.M.; Yahia, A. New approach to assess build-up of cement-based suspensions. Cem. Concr. Res. 2016, 85, 174–182.
- Zhang, K.; Mezhov, A.; Schmidt, W. Chemical and thixotropic contribution to the structural build-up of cementitious materials. Constr. Build. Mater. 2022, 345, 128307.
- Roussel, N.; Ovarlez, G.; Garrault, S.; Brumaud, C. The origins of thixotropy of fresh cement pastes. Cem. Concr. Res. 2012, 42, 148–157.
- Ukrainczyk, N.; Thiedeitz, M.; Kränkel, T.; Koenders, E.; Gehlen, C. Modeling SAOS Yield Stress of Cement Suspensions: Microstructure-Based Computational Approach. Materials 2020, 13, 2769.
- Conte, T.; Chaouche, M. Rheological behavior of cement pastes under Large Amplitude Oscillatory Shear. Cem. Concr. Res. 2016, 89, 332–344.
- Schultz, M.A.; Struble, L.J. Use of oscillatory shear to study flow behavior of fresh cement paste. Cem. Concr. Res. 1993, 23, 273–282.
- Kawashima, S.; Chaouche, M.; Corr, D.J.; Shah, S.P. Rate of thixotropic rebuilding of cement pastes modified with highly purified attapulgite clays. Cem. Concr. Res. 2013, 53, 112–118.
- Nachbaur, L.; Mutin, J.C.; Nonat, A.; Choplin, L. Dynamic mode rheology of cement and tricalcium silicate pastes from mixing to setting. Cem. Concr. Res. 2001, 31, 183–192.
- Kolawole, J.T.; Combrinck, R.; Boshoff, W.P. Rheo-viscoelastic behaviour of fresh cement-based materials: Cement paste, mortar and concrete. Constr. Build. Mater. 2020, 248, 118667.
- Thiedeitz, M.; Kränkel, T.; Gehlen, C. Viscoelastoplastic classification of cementitious suspensions: Transient and non-linear flow analysis in rotational and oscillatory shear flows. Rheol. Acta 2022, 61, 549–570.
- Mahaut, F.; Mokéddem, S.; Chateau, X.; Roussel, N.; Ovarlez, G. Effect of coarse particle volume fraction on the yield stress and thixotropy of cementitious materials. Cem. Concr. Res. 2008, 38, 1276–1285.
- Perrot, A.; Lecompte, T.; Khelifi, H.; Brumaud, C.; Hot, J.; Roussel, N. Yield stress and bleeding of fresh cement pastes. Cem. Concr. Res. 2012, 42, 937–944.
- Roussel, N. Steady and transient flow behaviour of fresh cement pastes. Cem. Concr. Res. 2005, 35, 1656–1664.
- El Bitouri, Y.; Azéma, N. Contribution of turbidimetry on the characterization of cement pastes bleeding. Adv. Cem. Res. 2023, 35, 180–190.
- Lei, W.-G.; Struble, L.J. Microstructure and Flow Behavior of Fresh Cement Paste. J. Am. Ceram. Soc. 1997, 80, 2021–2028.
- Papo, A.; Piani, L. Flow Behavior of Fresh Portland Cement Pastes. Part. Sci. Technol. 2004, 22, 201–212.
- Ivanov, Y.P.; Roshavelov, T.T. Flow behaviour of modified cement pastes. Cem. Concr. Res. 1993, 23, 803–810.
- Colombo, A.; Geiker, M.R.; Justnes, H.; Lauten, R.A.; De Weerdt, K. On the effect of calcium lignosulfonate on the rheology and setting time of cement paste. Cem. Concr. Res. 2017, 100, 435–444.
- Plank, J.; Sakai, E.; Miao, C.W.; Yu, C.; Hong, J.X. Chemical admixtures—Chemistry, applications and their impact on concrete microstructure and durability. Cem. Concr. Res. 2015, 78, 81–99.
- Barneoud-Chapelier, A.; Le Saout, G.; Azéma, N.; El Bitouri, Y. Effect of polycarboxylate superplasticizer on hydration and properties of belite ye’elimite ferrite cement paste. Constr. Build. Mater. 2022, 322, 126483.
- Otsubo, Y.; Miyai, S.; Umeya, K. Time-dependent flow of cement pastes. Cem. Concr. Res. 1980, 10, 631–638.
- Emoto, T.; Bier, T.A. Rheological behavior as influenced by plasticizers and hydration kinetics. Cem. Concr. Res. 2007, 37, 647–654.
- Krieger, I.M.; Dougherty, T.J. A Mechanism for Non-Newtonian Flow in Suspensions of Rigid Spheres. Trans. Soc. Rheol. 1959, 3, 137–152.
- Mahaut, F.; Chateau, X.; Coussot, P.; Ovarlez, G. Yield stress and elastic modulus of suspensions of noncolloidal particles in yield stress fluids. J. Rheol. 2008, 52, 287–313.
- Flatt, R.J.; Bowen, P. Yodel: A yield stress model for suspensions. J. Am. Ceram. Soc. 2006, 89, 1244–1256.
- Odler, I.; Duckstein, U.; Becker, T. On the combined effect of water solubles lignosulfonates and carbonates on portland cement and clinker pastes 1. Physical properties. Cem. Concr. Res. 1978, 8, 469–479.
- Roy, D.M.; Asaga, K. Rheological properties of cement mixes: III. The effects of mixing procedures on viscometric properties of mixes containing superplasticizers. Cem. Concr. Res. 1979, 9, 731–739.
- Brady, J.F.; Bossis, G. The rheology of concentrated suspensions of spheres in simple shear flow by numerical simulation. J. Fluid Mech. 1985, 155, 105–129.
- Hoffman, R.L. Explanations for the cause of shear thickening in concentrated colloidal suspensions. J. Rheol. 1998, 42, 111–123.
- Ovarlez, G.; Bertrand, F.; Rodts, S. Local determination of the constitutive law of a dense suspension of noncolloidal particles through magnetic resonance imaging. J. Rheol. 2006, 50, 259–292.
- Barnes, H.A. Shear-Thickening (“Dilatancy”) in Suspensions of Nonaggregating Solid Particles Dispersed in Newtonian Liquids. J. Rheol. 1989, 33, 329–366.
- Jiao, D.; Lesage, K.; Yardimci, M.Y.; El Cheikh, K.; Shi, C.; De Schutter, G. Rheological behavior of cement paste with nano-Fe3O4 under magnetic field: Magneto-rheological responses and conceptual calculations. Cem. Concr. Compos. 2021, 120, 104035.
- Jiao, D.; Shi, C.; De Schutter, G. Magneto-responsive structural build-up of highly flowable cementitious paste in the presence of PCE superplasticizer. Constr. Build. Mater. 2022, 327, 126925.
- Barnes, H.A. Thixotropy—A review. J. Nonnewton. Fluid Mech. 1997, 70, 1–33.
- Lapasin, R.; Longo, V.; Rajgelj, S. Thixotropic behaviour of cement pastes. Cem. Concr. Res. 1979, 9, 309–318.
- Roussel, N. A thixotropy model for fresh fluid concretes: Theory, validation and applications. Cem. Concr. Res. 2006, 36, 1797–1806.
- Petkova, V.; Samichkov, V. Some influences on the thixotropy of composite slag Portland cement suspensions with secondary industrial waste. Constr. Build. Mater. 2007, 21, 1520–1527.
- Billberg, P. Form Pressure Generated by Self-Compacting Concrete: Influence of Thixotropy and Structural Behaviour at Rest. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2006.
- Zhang, Z.; Jia, Z.; Shi, J.; Jiang, Y.; Banthia, N.; Zhang, Y. Clarifying and quantifying the driving force for the evolution of static yield stress of cement pastes. Cem. Concr. Res. 2023, 167, 107129.
