Graph Burning: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Jesús García Díaz

The graph burning problem is a relatively new combinatorial optimization problem that helps quantify a graph's vulnerability. It is defined in terms of a fundamental diffusion model.

  • graph burning
  • social contagion

1. Introduction

The graph burning problem (GBP) is an NP-hard combinatorial optimization problem introduced in 2014 in the context of social contagion [1]. This problem, concerned with the sequential spread of information over a graph, considers that information can be spread from different places and times [1][2]. In this entry, by graph we refer to an undirected simple graph [3]. Computer network message propagation is an example of a real-world problem that the GBP may model; in this scenario, an initial spreading entity can send a message one host at a time, while these hosts can propagate the message only to their neighbors [4][5]. The GBP may model other real-world problems: social contagion in social networks and the spread of viral infections under a very idealistic context [6].
The GBP receives a graph G=(V,E) as input, and its goal is to find a minimum length sequence of vertices (𝑠1,𝑠2,…,𝑠k) that burns all graph’s vertices by following the burning process. This process consists of repeating the following steps from 𝑖=1 to k, where all vertices are unburned at the beginning, and once a vertex is burned, it remains in that state.

    a) The neighbors of the burned vertices get burned.

    b) Vertex 𝑠i gets burned.

Figure 1 shows a simple example of the burning process. The length of an optimal burning sequence for a given graph G is denoted by b(G) and is known as the burning number.

Figure 1. An optimal burning sequence for a nine vertices path is (𝑣3,𝑣7,𝑣9). The burning process of this sequence is depicted by each 𝑖 ∈ {1,2,3} with its corresponding steps a and b. Notice that vertex 𝑣3 burns all vertices at distance at most 2, vertex 𝑣7 burns all vertices at distance at most 1, and vertex 𝑣9 only burns itself.

Since the above example is too simple, Figures 2-4 show the optimal burning sequence of some classical graph instances from the literature.

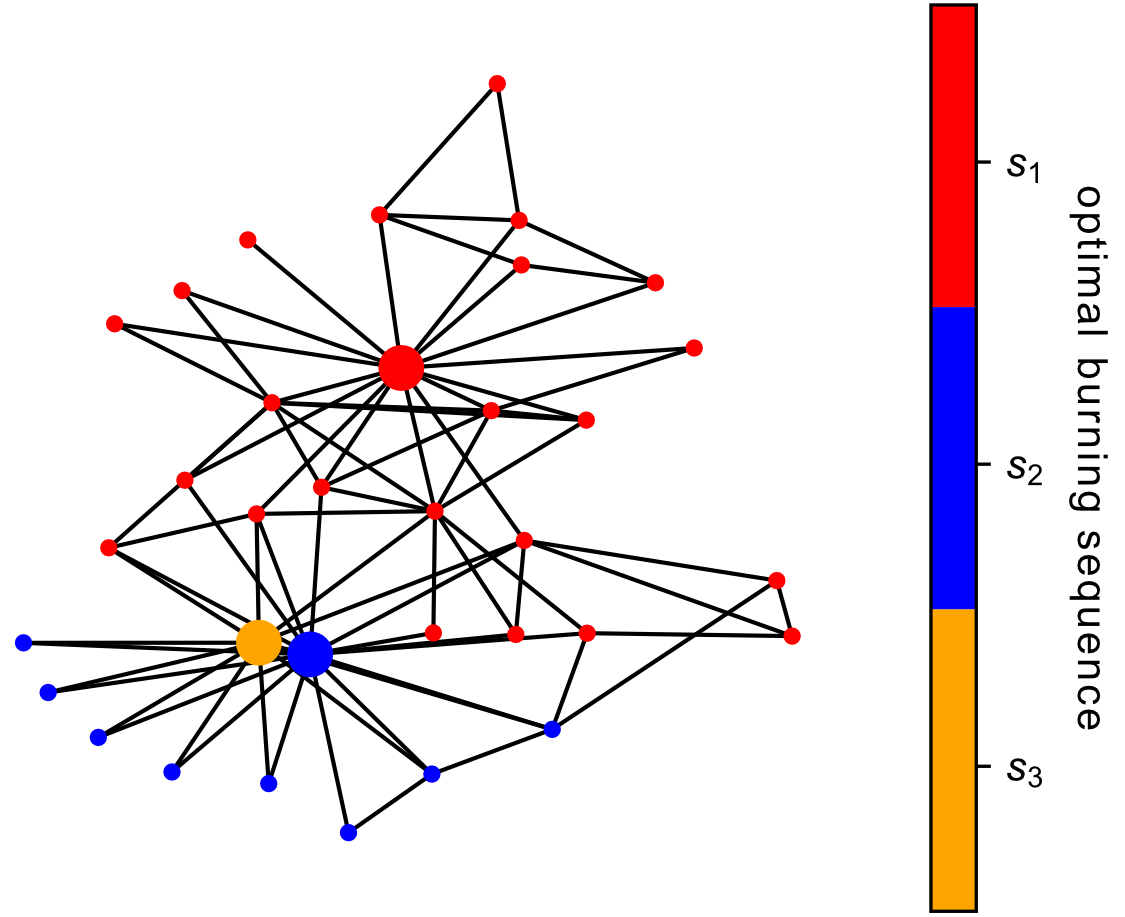
Figure 2. An optimal burning sequence of Zachary's karate club graph.

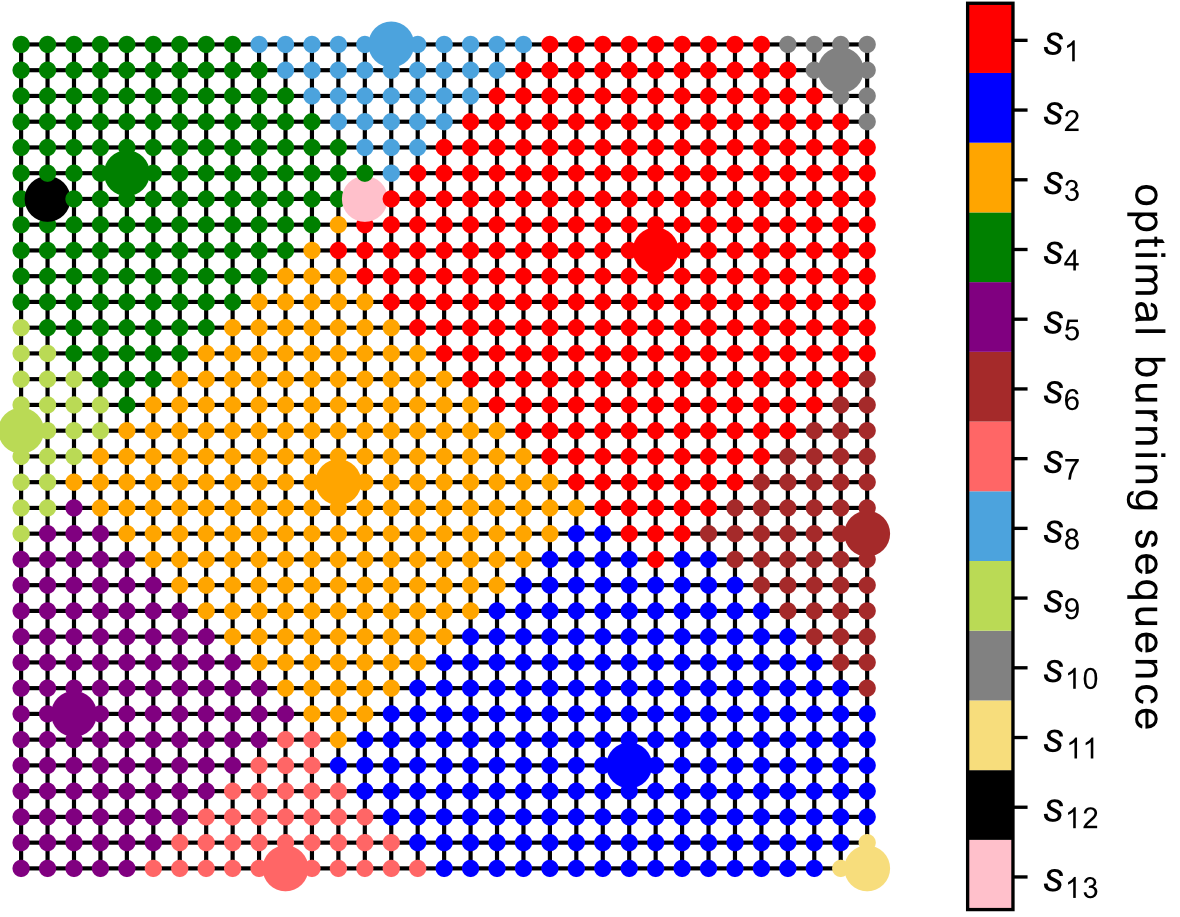
Figure 3. An optimal burning sequence of a 33x33 2D lattice.

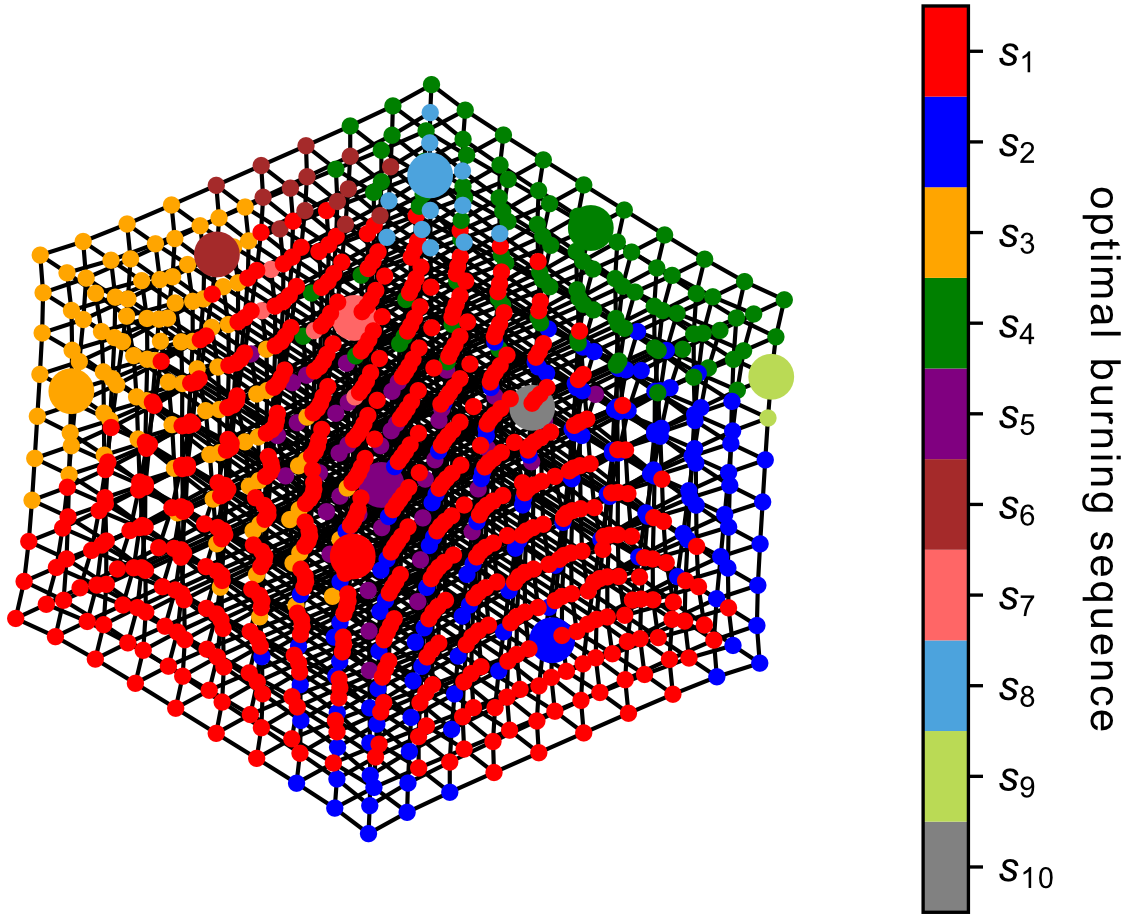
Figure 4. An optimal burning sequence of a 10x10x10 3D lattice.

2. Graph Burning: Properties, Models, and Algorithms

The decision version of the GBP is NP-complete. This problem receives as input a graph 𝐺=(𝑉,𝐸) and a positive integer k; it asks if a burning sequence of length at most k exists. The problem remains NP-complete when restricted to trees of maximum degree three, chordal graphs, bipartite graphs, planar graphs, spider graphs, and disconnected graphs [2]. The optimization version of the problem also remains NP-hard for trees and graphs with disjoint paths [7]. Regarding arbitrary graphs, two approximation algorithms are reported in the literature; they have an approximation factor of 3 and 3−2/𝑏(𝐺), respectively [7][8]. There is a 2-approximation algorithm for trees, a 1.5-approximation algorithm for graphs with disjoint paths, and a 2-approximation algorithm for square grids [6][7]. For minimization problems, a 𝜌-approximation algorithm returns solutions of size at most 𝜌·𝑂𝑃𝑇, where 𝑂𝑃𝑇 is the size of the optimal solution and 𝜌≥1. In the case of maximization problems, a 𝜌-approximation algorithm returns solutions of size at least (1/𝜌)·𝑂𝑃𝑇 [9]. Besides approximation algorithms, some heuristics have been proposed too [4][5]; these are mainly based on centrality measures and binary search over the set of possible values of 𝑏(𝐺). The GBP has been formulated using integer linear programming and constraint satisfaction problems. Using these formulations and off-the-shelf optimization software, graphs with up to 5908 vertices have been solved to proven optimality [10].
The GBP has been approached mostly from a theoretical point of view. As a result, many of its properties over specific graph families have been identified. Among these families are paths [2][7], trees [2][7], grids [6], intervals [6], fences [11], theta [12], spiders [13], path-forests [2][7][13], caterpillars [14], products [15], and generalized Petersen graphs [16]. Some of the main properties of the GBP are the following. All paths and cycles G of order n have 𝑏(𝐺)=⌈𝑛1/2⌉, all graphs G with a Hamiltonian path have 𝑏(𝐺)≤⌈𝑛1/2⌉ [1][2], all spiders and caterpillars G have 𝑏(𝐺)≤⌈𝑛1/2⌉ [13][14], all complete graphs G of order at least two have 𝑏(𝐺)=2, and all perfect binary trees G of depth r have 𝑏(𝐺)=𝑟+1. Based on these properties, a conjecture on the upper bound of the burning number of connected graphs was formulated by Bonato et al. [1]: Every connected graph G of order n has burning number b(G)≤⌈𝑛1/2⌉. This conjecture, known as the burning number conjecture, is one of the most important open questions in the area. To date, the best-known bound for the burning number of arbitrary connected graphs is 𝑏(𝐺)≤⌈(4·𝑛/3)1/2⌉+1 [17].
The GBP resembles other NP-hard problems, such as the vertex k-center problem (VKCP) and the firefighter problem (FP). The VKCP consists of finding the best location for a set of 𝑘 ∈ ℤ centers, where such locations are the ones that minimize the maximum distance a customer has to travel to its nearest center [18][19][20]. Although the VKCP and the GBP are different, their approximation algorithms are conceptually similar [7][8][20]. This similarity comes from the fact that the VKCP has a polynomial-time reduction to the minimum dominating set problem, which can be viewed as the problem of burning all vertices in parallel in one single step [20][21][22][23]. Regarding the FP, it aims at protecting vertices from burning given an initial set of fire sources [24][25][26]. Although GBP and FP have different goals, the latter’s integer linear program (ILP) served as inspiration to define an integer linear program for the GBP [10].

This entry is adapted from the peer-reviewed paper 10.3390/math10152777

References

  1. Bonato, A.; Janssen, J.; Roshanbin, E. Burning a graph as a model of social contagion. In International Workshop on Algorithms and Models for the Web-Graph; Springer: Berlin/Heidelberg, Germany, 2014; pp. 13–22.
  2. Bessy, S.; Bonato, A.; Janssen, J.; Rautenbach, D.; Roshanbin, E.; Burning a graph is hard. Discret. Appl. Math. 2017, 232, 73-87, .
  3. Diestel, R.. Graph Theory; Springer Graduate Texts in Mathematics: Springer: Berlin/Heidelberg, Germany, 2017; pp. 2.
  4. Šimon, M.; Huraj, L.; Luptáková, I.D.; Pospíchal, J.; Heuristics for spreading alarm throughout a network. Appl. Sci. 2019, 9, 3269, .
  5. Gautam, R.H.; Kare, A.S.; Surampudi, D.B.; Faster heuristics for graph burning. Appl. Intell. 2021, 52, 1351–1361, .
  6. Gupta, A.T.; Lokhande, S.A.; Mondal, K. Burning grids and intervals. In Proceedings of the Algorithms and Discrete Applied Mathematics, Rupnagar, India, 11–13 February 2021; pp. 66–79
  7. Bonato, A.; Kamali, S. Approximation algorithms for graph burning. In Proceedings of the International Conference on Theory and Applications of Models of Computation, Kitakyushu, Japan, 13–16 April 2019; pp. 74–92.
  8. García-Díaz, J.; Pérez-Sansalvador, J.C.; Rodríguez-Henríquez, L.M.X.; Cornejo-Acosta, J.A.; Burning Graphs Through Farthest-First Traversal. IEEE Access 2022, 10, 30395–30404, .
  9. Vazirani, V.V.. Approximation Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; pp. 1.
  10. García-Díaz, J.; Rodríguez-Henríquez, L.M.X.; Pérez-Sansalvador, J.C.; Pomares-Hernández, S.E.; Graph Burning: Mathematical Formulations and Optimal Solutions. Mathematics 2022, 10, 2777, .
  11. Bonato, A.; English, S.; Kay, B.; Moghbel, D.; Improved bounds for burning fence graphs. Graphs Comb. 2021, 37, 2761–2773, .
  12. Liu, H.; Zhang, R.; Hu, X.; Burning number of theta graphs. Appl. Math. Comput. 2019, 361, 246–257, .
  13. Bonato, A.; Lidbetter, T.; Bounds on the burning numbers of spiders and path-forests. Theor. Comput. Sci. 2019, 794, 12-19, .
  14. Liu, H.; Hu, X.; Hu, X.; Burning number of caterpillars. Discret. Appl. Math. 2020, 284, 332–340, .
  15. Mitsche, D.; Prałat, P.; Roshanbin, E.; Burning number of graph products. Theor. Comput. Sci. 2018, 746, 124–135, .
  16. Sim, K.A.; Tan, T.S.; Wong, K.B.; On the burning number of generalized petersen graphs. Bull. Malaysian Math. Sci. 2018, 41, 1657–1670, .
  17. Bastide, P.; Bonamy, M.; Bonato, A.; Charbit, P.; Kamali, S.; Pierron, T.; Rabie, M. Improved Pyrotechnics: Closer to the Burning Number Conjecture. Preprint. 2022. Available online: https://arxiv.org/abs/2110.10530 (accessed on 31 July 2022).
  18. Gonzalez, T.F.; Clustering to minimize the maximum intercluster distance. Theor. Comput. Sci. 1985, 38, 293–306, .
  19. Hochbaum, D.S.; Shmoys, D.B.; A best possible heuristic for the k-center problem. Math. Oper. Res. 1985, 10, 180–184, .
  20. Garcia-Diaz, J.; Menchaca-Mendez, R.; Menchaca-Mendez, R.; Hernández, S.P.; Pérez-Sansalvador, J.C.; Lakouari, N.; Approximation Algorithms for the Vertex K-Center Problem: Survey and Experimental Evaluation. IEEE Access 2019, 7, 109228–109245, .
  21. Cornejo Acosta, J.A.; García Díaz, J.; Menchaca-Méndez, R.; Menchaca-Méndez, R.; Solving the Capacitated Vertex K-Center Problem through the Minimum Capacitated Dominating Set Problem. Mathematics 2020, 8, 1551, .
  22. Grandoni, F.; A note on the complexity of minimum dominating set. J. Discret. Algorithms 2006, 4, 209–214, .
  23. Hernández-Gómez, J.C.; Reyna-Hérnandez, G.; Romero-Valencia, J.; Rosario Cayetano, O.; Transitivity on Minimum Dominating Sets of Paths and Cycles. Symmetry 2020, 12, 2053, .
  24. Hartnell, B. Firefighter! An application of domination. Presentation. In Proceedings of the 25th Manitoba Conference on Combinatorial Mathematics and Computing, Winnipeg, MB, Canada, 29 September–1 October 1995.
  25. Develin, M.; Hartke, S.G.; Fire containment in grids of dimension three and higher. Discrete Appl. Math. 2007, 155, 2257–2268, .
  26. García-Martínez, C.; Blum, C.; Rodriguez, F.J.; Lozano, M.; The firefighter problem: Empirical results on random graphs. Comput. Oper. Res. 2015, 60, 55–66, .
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback