Multiple Traveling Salesperson Problems: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
José Alejandro Cornejo-Acosta
,
Jesús García-Díaz
,
Julio César Pérez-Sansalvador
,
Carlos Segura

Multiple traveling salesperson problems (mTSP) are a collection of problems that generalize the classical traveling salesperson problem (TSP). In a nutshell, an mTSP variant seeks a minimum cost collection of m paths that visit all vertices of a given weighted complete graph.

  • integer programming
  • multiple traveling salesperson problem
  • depot-free mTSP

1. Introduction

The multiple traveling salesperson problem has received different labels over time, mainly because it is not a single problem but a collection of them. Thus, this text refers to this collection as the multiple traveling salesperson problems (mTSP). These problems are relevant in several social situations, including cooperative missions, transportation, delivery, disaster management, precision agriculture, and many others [1].
Each variant of mTSP is a generalization of the NP-hard traveling salesperson problem (TSP). The goal of TSP is to find a minimum-cost closed path a salesperson must follow to visit a set of given cities. In more detail, given a weighted complete graph G=(V, E), the TSP seeks a closed path that visits all vertices once, minimizing the path’s cost [2][3][4]. In the mTSP, the input is a weighted complete graph G=(V, E) and a positive integer m; its goal is to find a set of m paths such that all vertices are visited once by some salesperson [4][5]. If the input graph is undirected (resp., directed), the problem is symmetric (resp., asymmetric). An mTSP variant receives particular adjectives depending on its characteristics: depot free (DF), single depot (S), multiple depots (M), closed paths (CP), open paths (OP), bounding constraints, etc. In most cases, the objective function to minimize is the sum of the paths’ costs (minsum) or the largest path (minmax or makespan); other objective functions might be considered, such as the cost of the largest edge (bottleneck).
The most widely studied members of the mTSP collection are single-depot mTSP (SmTSP) and multiple-depots mTSP (MmTSP). However, the depot-free mTSP (DFmTSP) variant has received less attention. In SmTSP, all salespersons must start and finish their path at a specific vertex (the depot), which is part of the input. In the fixed-destination multiple-depots mTSP (FD-MmTSP), m depots are part of the input, and each salesperson must start and finish their path at their respective depot. In the non-fixed-destination multiple-depots mTSP (NFD-MmTSP), each salesperson can finish their path at a different depot. In DFmTSP, the depot concept is not involved. Therefore, it seeks a disjoint collection of closed paths that visit all vertices. In all these variants, every solution consists of exactly m paths, and the path followed by each salesperson is closed. Nevertheless, if the salespersons are constrained to follow open paths (i.e., they do not need to return to their depot), researchers refer to the problem as an open-paths (OP) variant. To clarify the difference between these variants, Figure 1 shows a set of optimal solutions for DFmTSP, SmTSP, and FD-MmTSP. In all these examples, each path must have between three and five vertices; this text refers to these as bounding constraints.
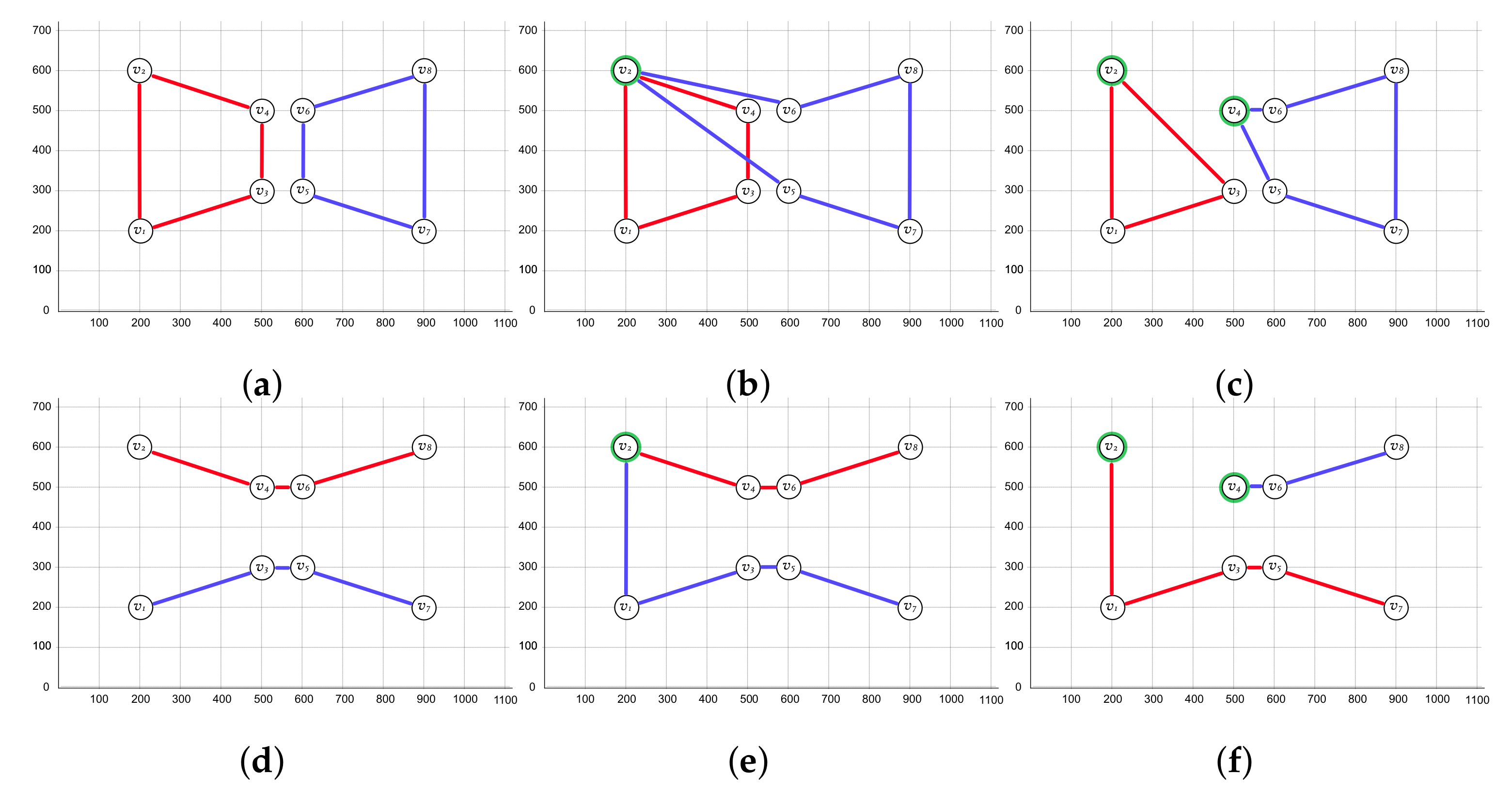
Figure 1. Optimal solutions for (a) closed-paths depot-free mTSP (CP-DFmTSP), (b) closed-paths single-depot mTSP (CP-SmTSP), and (c) closed-paths fixed-destination multiple-depots mTSP (CP-FD-MmTSP). The objective function is minsum, the number of salespersons is two (m=2), each path must have between three and five vertices (bounding constraints), the cost of each edge equals the euclidean distance between its vertices, and the depots are marked in green. Subfigures (d–f) correspond to the respective open-paths (OP) variants.
Although there are some surveys on mTSP [1][6][7], they are not structured in chronological order; order that might shed some light on how DFmTSP has received less attention than other variants. Therefore, the following sections give a general overview of how the study of mTSP has evolved. To maintain simplicity, researchers stuck to the broad categories: SmTSP, MmTSP, and DFmTSP. Namely, sophisticated requirements studied in some examined papers (objective functions, paths’ properties, time windows, etc.) are omitted. 

2. TSP and SmTSP

TSP is among the most popular NP-hard combinatorial optimization problems. Its first explicit appearance in the scientific literature dates from 1954 [2], and its first mathematical formulations from 1959 and 1960 [3][4]. Interestingly, the authors of these early papers stated the problem using the depot concept, a special vertex where the salesperson starts and finishes their path. Nevertheless, it is easy to observe that the depot plays only a symbolic and didactic role, i.e., it is equivalent to stating that the path must be closed. However, the first member of the mTSP collection to be studied was SmTSP; in this version of the problem, all salespersons start and finish their path at the same vertex (the depot), which is part of the input. The most usual objective function to minimize in both TSP and mTSP is minsum, i.e., the total length of the paths. Naturally, mTSP with one salesperson (m=1) is equivalent to TSP; therefore, mTSP is NP-hard too.

3. mTSP from 1960 to 1975

Although the first IP for SmTSP dates from 1960 [4], the problem started gaining more attention between 1973 and 1975, when more efficient mathematical formulations were introduced [5][8]; the authors did not refer to the problem as SmTSP but as mTSP. For that reason, many use both names interchangeably. However, to avoid confusion, researchers refer to this variant only as SmTSP. Something remarkable about SmTSP is that it can be transformed into TSP by adding some extra vertices to the original graph [8].

4. mTSP from 1976 to 1995

SmTSP and many of its variants continued being modeled using integer programming. Most of these formulations were based on transformations to TSP [9][10][11][12][13][14][15][16][17], and only a few were direct [18][19]. Some variants included the case where at most m salespersons are in the solution; some refer to such variant as the SmTSP with fixed charges [11], and others as variable SmTSP [20]. In this variant, each salesperson incurs some cost that is considered in the objective function. Notice that the variant identified as SmTSP is where exactly m salespersons are in the solution. The exact algorithms designed for this problem within this period were based mainly on Benders decomposition [12], cutting planes [18], and branch and bound [21]. In this same period, some heuristics for SmTSP were introduced too [17][22][23][24][25]. By 1995, SmTSP with a minsum objective function was the most studied member of the mTSP collection; only the MmTSP with two salespersons (m=2) was mentioned and reduced to TSP in 1980 [13]. It was until 1995 that MmTSP was reduced to TSP [16]. In this period, only a tabu search metaheuristic approach was developed for SmTSP [26].

5. mTSP from 1996 to 2005

MmTSP started gaining more attention. More heuristics and metaheuristics considering minsum and minmax objective functions for SmTSP, MmTSP, and DFmTSP were introduced too, for instance, neural networks [27][28][29], genetic algorithms [30][31][32], particle swarm optimization [31], evolutionary strategies [31], and simulated annealing [33]. It is crucial to emphasize that during this period, DFmTSP started being spotted by some authors [30][31][34]. Although some of them referred to the problem as mTSP or SmTSP, a closer inspection reveals that the problem they worked with was actually DFmTSP.

6. mTSP from 2006 to Date

The interest in SmTSP, MmTSP, DFmTSP, and their variants continued growing. The interest in the minmax objective function grew too. However, most of the efforts were still hoarded by SmTSP and the minsum objective function. In this period, many heuristics [35][36][37][38][39], exact algorithms [40][41][42][43][44][45], and IPs [6][40][42][46][47][48][49][50][51][52] were proposed. Metaheuristics dominated the scene with neural networks [29][53][54], genetic algorithms [55][56][57][58][59][60][61][62][63][64][65][66][67][68][69][70][71][72][73][74][75][76][77][78][79][80], clustering strategies [81], ant colony optimization [74][82][83][84][85][86][87], firefly algorithm [87], ant colony system [88][89], market-based algorithms [90][91], imperialist competitive algorithm [92], tabu search [54], gravitational emulation local search algorithm [93], variable neighborhood search [94][95][96][97], bee colony optimization [98], invasive weed optimization [98], wolf pack search algorithm [99], discrete pigeon optimization [100], reinforcement learning [101], evolutionary strategies [102], hybrid search [103], memetic search [103], simulated annealing [104], and bees algorithm [105]. As in years before, only a few authors worked on DFmTSP. Remarkably, until 2017 and 2021, the first reported IPs for DFmTSP were published [49][102]. Recently, more integer programs were proposed for the DFmTSP which exploits a relationship between the FD-MmTSP and the DFmTSP [1].

7. Approximation Algorithms

Only a few approximation algorithms have been designed for some variants of mTSP. For that reason, this paragraph presents an independent account of such algorithms; these include a (4/3)(4/3)- and a (3/2)(3/2)-approximation algorithm for the SmTSP and MmTSP on a tree with two salespersons (𝑚=2) and minmax objective function [106], a (2−2/(m+1))-approximation algorithm for DFmTSP on trees with m traveling salespersons and minmax objective function [107], a faster approximation algorithm with the same approximation factor for the same problem [108], a 2-approximation algorithm for MmTSP with triangle inequality [109], a (3/2)(3/2)-approximation algorithm for MmTSP with triangle inequality and a constant number of depots [110], a (2−1/𝑘)-approximation algorithm for MmTSP [111], a (2−1/(2𝑘))-approximation algorithm for MmTSP [112], a (1+𝜖)-approximation algorithm for SmTSP on a tree with minmax objective function, with the depot located at the tree’s root [113], and a (1+𝜖)-approximation algorithm for the SmTSP on a spider, with the depot located at its center [114].

8. When Depots Are Unknown or Unnecessary

Table 1 shows the main scope of the examined papers, and Figure 2 shows how they distribute over time. From Table 1 and Figure 2, we can observe that, on the one hand, SmTSP and MmTSP have been the most studied variants. On the other hand, DFmTSP has not received as much attention; only two IPs have been published, and they are relatively recent and have a limited scope [49][102]. Since the classical TSP does not require the depot concept to be formulated, researchers believe that DFmTSP should be considered an essential member of the mTSP collection and should receive more attention. Additionally, this variant is more adequate for specific applications, such as submarine patrol routing [34], supervisor allocation [48][49], and some variations of the job scheduling problem [30]. In a nutshell, DFmTSP is a better model for social problems where depots are unknown or unnecessary. Cornejo-Acosta et al.  [1] introduce novel IPs for DFmTSP and its main variants:
  • Closed paths (CP).
  • Open paths (OP).
  • Minsum objective function.
  • Minmax objective function.
  • Bounding constraints:
    -
    Lower bound on the number of vertices per path.
    -
    Upper bound on the number of vertices per path.
As a byproduct, the proposed IPs of Cornejo-Acosta et al. [1] are adapted to a combination of FD-MmTSP and DFmTSP, namely, a variant where fewer than m depots are part of the input, but the solution consists of exactly m paths. This variant can be helpful in situations where only a few depots have already been selected. Thus, deciding the location of the remaining depots is part of the problem.
Figure 2. Published papers directly related to mTSP over time.
Table 1. Main categories and scope of related work. S, M, and DF stand for single depot, multiple depot, and depot free, respectively.
Main Scope mTSP Reference
Integer programming S
M
DF		 [4][5][6][8][9][10][11][12][13][14][15][16][17][18][19][20][47]
[6][13][16][40][42][45][46][48][49][50][51][52]
[34][49][102]
Exact algorithm S
M
DF		 [12][18][21][43][44]
[40][41][42][43][45][113]
-
Heuristic S
M
DF		 [17][22][23][24][25][38][39]
[36][37][38]
[35][38]
Metaheuristic S [26][27][28][29][32][33][53][54][55][56][57][58][59][60][61][62][63][65][66][67][68][69][70][71][72][74][76][78][79]
[81][82][83][85][86][88][89][92][93][94][95][96][98][99][100][101][102][103][105][115]
M
DF		 [80][84][86][87][90][91][97][102][103][116]
[30][31][64][73][75][77][102][104]
Approximation algorithm S
M
DF		 [106][114]
[106][108][109][110][111][112][113]
[107]

This entry is adapted from the peer-reviewed paper 10.3390/math11133014

References

  1. Cheikhrouhou, O.; Khoufi, I. A comprehensive survey on the Multiple Traveling salesman Problem: Applications, approaches and taxonomy. Comput. Sci. Rev. 2021, 40, 100369.
  2. Dantzig, G.B.; Fulkerson, D.R.; Johnson, S.M. Solution of a Large-Scale Traveling-Salesman Problem; RAND Corporation: Santa Monica, CA, USA, 1954; pp. 393–410.
  3. Dantzig, G.B.; Fulkerson, D.R.; Johnson, S.M. On a linear-programming, combinatorial approach to the traveling-salesman problem. Oper. Res. 1959, 7, 58–66.
  4. Miller, C.E.; Tucker, A.W.; Zemlin, R.A. Integer programming formulation of traveling salesman problems. J. ACM 1960, 7, 326–329.
  5. Svestka, J.A.; Huckfeldt, V.E. Computational Experience with an M-salesperson Traveling salesman Algorithm. Manag. Sci. 1973, 19, 790–799.
  6. Bektas, T. The multiple traveling salesman problem: An overview of formulations and solution procedures. Omega 2006, 34, 209–219.
  7. Kara, I.; Bektas, T. Integer linear programming formulations of multiple salesman problems and its variations. Eur. J. Oper. Res. 2006, 174, 1449–1458.
  8. Bellmore, M.; Hong, S. Transformation of multisalesperson problem to the standard traveling salesman problem. J. ACM 1974, 21, 500–504.
  9. Gavish, B. A note on the formulation of the m-salesman traveling salesperson problem. Manag. Sci. 1976, 22, 704–705.
  10. Svestka, J.A. Response to A note on the formulation of the m-salesman traveling salesperson problem. Manag. Sci. 1976, 22, 706.
  11. Hong, S.; Padberg, M.W. A note on the symmetric multiple traveling salesman problem with fixed charges. Oper. Res. 1977, 25, 871–874.
  12. Gavish, B.; Graves, S.C. The Travelling Salesman Problem and Related Problems; Massachusetts Institute of Technology, Operations Research Center: Cambridge, MA, USA, 1978.
  13. Rao, M.R. A note on the multiple traveling salesmen problem. Oper. Res. 1980, 28, 628–632.
  14. Discenza, J.H. A more compact formulation of the symmetric multiple traveling salesman problem with fixed charges. Networks 1981, 11, 73–75.
  15. Jonker, R.; Volgenant, T. An improved transformation of the symmetric multiple traveling salesman problem. Oper. Res. 1988, 36, 163–167.
  16. Guoxing, Y. Transformation of multidepot multisalesmen problem to the standard travelling salesman problem. Eur. J. Oper. Res. 1995, 81, 557–560.
  17. Wacholder, E.; Han, J.; Mann, R.C. A neural network algorithm for the multiple traveling salesmen problem. Biol. Cybern. 1989, 61, 11–19.
  18. Laporte, G.; Yves, N. A cutting planes algorithm for the m-salesmen problem. J. Oper. Res. Soc. 1980, 31, 1017–1023.
  19. Ali, A.I.; Kennington, J.L. The asymmetric M-travelling salesmen problem: A duality based branch-and-bound algorithm. Discret. Appl. Math. 1986, 13, 259–276.
  20. Ali, A.; Kennington, J. The M-Travelling Salesmen Problem; Department of Operations Research, Southern Methodist University: Dallas, TX, USA, 1980.
  21. Gavish, B.; Srikanth, K. An optimal solution method for large-scale multiple traveling salesmen problems. Oper. Res. 1986, 34, 698–717.
  22. Potvin, J.Y.; Lapalme, G.; Rousseau, J.M. A generalized k-opt exchange procedure for the MTSP. INFOR Inf. Syst. Oper. Res. 1989, 27, 474–481.
  23. Hsu, C.Y.; Tsai, M.H.; Chen, W.M. A study of feature-mapped approach to the multiple travelling salesmen problem. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 11–14 June 1991; pp. 1589–1592.
  24. Gromicho, J.; Paixão, J.; Bronco, I. Exact solution of multiple traveling salesman problems. In Combinatorial Optimization; Akgül, M., Hamacher, H.W., Tüfekçi, S., Eds.; NATO ASI Series; Springer: Berlin/Heidelberg, Germany, 1992; Volume 82, pp. 291–292. ISBN 978-3-642-77489-8.
  25. Russell, R.A. An Effective Heuristic for the M-Tour Traveling salesman Problem with Some Side Conditions. Oper. Res. 1977, 25, 517–524.
  26. França, P.M.; Gendreau, M.; Laporte, G.; Müller, F.M. The m-traveling salesman problem with minmax objective. Transp. Sci. 1995, 29, 267–275.
  27. Modares, A.; Somhom, S.; Enkawa, T. A self-organizing neural network approach for multiple traveling salesman and vehicle routing problems. Int. Trans. Oper. Res. 1999, 6, 591–606.
  28. Somhom, S.; Modares, A.; Enkawa, T. Competition-based neural network for the multiple travelling salesmen problem with minmax objective. Comput. Oper. Res. 1999, 26, 395–407.
  29. Faigl, J.; Kulich, M.; Preucil, L. Multiple traveling salesmen problem with hierarchy of cities in inspection task with limited visibility. In Proceedings of the 5th Workshop on Self-Organizing Maps, Paris, France, 5–8 September 2005; pp. 91–98.
  30. Tang, L.; Liu, J.; Rong, A.; Yang, Z. A multiple traveling salesman problem model for hot rolling scheduling in Shanghai Baoshan Iron & Steel Complex. Eur. J. Oper. Res. 2000, 124, 267–282.
  31. Sofge, D.; Schultz, A.; De Jong, K. Evolutionary Computational Approaches to Solving the Multiple Traveling salesman Problem Using a Neighborhood Attractor Schema. In Applications of Evolutionary Computing; Cagnoni, S., Gottlieb, J., Hart, E., Middendorf, M., Raidl, G.R., Eds.; EvoWorkshops, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2279, pp. 153–162. ISBN 978-3-540-43432-0.
  32. Carter, A.E. Design and Application of Genetic Algorithms for the Multiple Traveling Salesperson Assignment Problem. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 21 April 2003.
  33. Song, C.H.; Lee, K.; Lee, W.D. Extended simulated annealing for augmented TSP and multi-salesmen TSP. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; pp. 2340–2343.
  34. Bugera, V. Properties of No-Depot MIN-MAX 2-Traveling-salesmen Problem. In Recent Developments in Cooperative Control and Optimization; Murphey, S., Pardalos, R., Cagnoni, P.M., Eds.; Cooperative Systems; Springer: Boston, MA, USA, 2004; Volume 3, pp. 45–59. ISBN 978-1-4613-7947-8.
  35. Byungsoo, N. Heuristic Approaches for No-Depot k-Traveling Salesmen Problem with a Minmax Objective. Master’s Thesis, Texas A&M University, College Station, TX, USA, May 2006.
  36. Hou, M.; Liu, D. A novel method for solving the multiple traveling salesmen problem with multiple depots. Chin. Sci. Bull. 2012, 57, 1886–1892.
  37. Wang, X.; Liu, D.; Hou, M. A novel method for multiple depot and open paths, Multiple Traveling salesmen Problem. In Proceedings of the IEEE 11th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 31 January–2 February 2013.
  38. Vandermeulen, I.; Groß, R.; Kolling, A. Balanced Task Allocation by Partitioning the Multiple Traveling Salesperson Problem. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems, Montréal, QC, Canada, 13–17 May 2019.
  39. Zheng, J.; Hong, Y.; Xu, W.; Li, W.; Chen, Y. An effective iterated two-stage heuristic algorithm for the multiple Traveling Salesmen Problem. Comput. Oper. Res. 2022, 143, 105772.
  40. Sundar, K.; Rathinamm, S. An exact algorithm for a heterogeneous, multiple depot, multiple traveling salesman problem. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 July 2015.
  41. Yadlapalli, S.; Malik, W.A.; Darbha, S.; Pachter, M. A Lagrangian-based algorithm for a Multiple Depot, Multiple Traveling salesmen Problem. Nonlinear Anal. Real World Appl. 2009, 10, 1990–1999.
  42. Bektas, T. Formulations and Benders decomposition algorithms for multidepot salesmen problems with load balancing. Eur. J. Oper. Res. 2012, 216, 83–93.
  43. Aguayo, M.M.; Sarin, S.C.; Sherali, H.D. Solving the Single and Multiple Asymmetric Traveling Salesmen Problems by Generating Subtour Elimination Constraints from Integer Solutions. IISE Trans. 2018, 50, 45–53.
  44. Campuzano, G.; Obreque, C.; Aguayo, M.M. Accelerating the Miller–Tucker–Zemlin model for the asymmetric traveling salesman problem. Expert Syst. Appl. 2020, 148, 113229.
  45. Benavent, E.; Martínez, A. Multi-depot Multiple TSP: A polyhedral study and computational results. Ann. Oper. Res. 2013, 207, 7–25.
  46. Oberlin, P.; Rathinam, S.; Darbha, S. A transformation for a Multiple Depot, Multiple Traveling Salesperson Problem. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009.
  47. Sarin, S.C.; Sherali, H.D.; Judd, J.D.; Tsai, P.F.J. Multiple asymmetric traveling salesmen problem with and without precedence constraints: Performance comparison of alternative formulations. Comput. Oper. Res. 2014, 51, 64–89.
  48. Assaf, M.; Ndiaye, M. A transformation for multiple depot multiple traveling salesman problem. In Proceedings of the International Conference on Engineering & MIS (ICEMIS), Monastir, Tunisia, 8–10 May 2017.
  49. Assaf, M. Transformations for Variants of the Travelling Salesman Problem and Applications. Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, April 2017.
  50. Kitjacharoenchai, P.; Ventresca, M.; Moshref-Javadi, M.; Lee, S.; Tanchoco, J.M.A.; Brunese, P.A. Multiple traveling salesman problem with drones: Mathematical model and heuristic approach. Comput. Ind. Eng. 2019, 129, 14–30.
  51. Aguayo, M.M.; Avilés, F.N.; Sarin, S.C.; Sherali, H.D. A Two-Index Formulation for the Fixed-Destination Multi-Depot Asymmetric Travelling Salesman Problem and Some Extensions. Informatica 2022, 33, 671–692.
  52. Kivelevitch, E.H.; Cohen, K.; Kumar, M. A binary programming solution to the min-max multiple-depots, multiple traveling salesman problem. In Proceedings of the AIAA () Conference, Boston, MA, USA, 19–22 August 2013.
  53. Qu, H.; Yu, Z.; Tang, H. A columnar competitive model for solving multi-traveling salesman problem. Chaos Solitons Fractals 2007, 31, 1009–1019.
  54. Matsuura, T.; Numata, K. Solving Min-Max Multiple Traveling salesman Problems by Chaotic Neural Network. In Proceedings of the International Symposium on Nonlinear Theory and Its Applications, Luzern, Switzerland, 14–18 September 2014.
  55. Carter, A.E.; Ragsdale, C.T. A new approach to solving the multiple traveling salesperson problem using genetic algorithms. Eur. J. Oper. Res. 2006, 175, 246–257.
  56. Brown, E.C.; Ragsdale, C.T.; Carter, A.E. A grouping genetic algorithm for the multiple traveling salesperson problem. Int. J. Inf. Technol. Decis. Mak. 2007, 6, 333–347.
  57. Sze, S.N.; Tiong, W.K. A Comparison between Heuristic and Meta-Heuristic Methods for Solving the Multiple Traveling salesman Problem. Int. J. Math. Comput. Sci. 2007, 1, 13–16.
  58. Zhao, F.; Dong, J.; Li, S.; Yang, X. An improved genetic algorithm for the multiple traveling salesman problem. In Proceedings of the Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008.
  59. Singh, A.; Baghel, A.S. A new grouping genetic algorithm approach to the multiple traveling salesperson problem. Soft Comput. 2009, 13, 95–101.
  60. Zhou, W.; Li, Y. An improved genetic algorithm for multiple traveling salesman problem. In Proceedings of the 2nd International Asia Conference on Informatics in Control, Automation and Robotics, Wuhan, China, 6–7 March 2010.
  61. Chen, S.H.; Chen, M.C. Operators of the Two-Part Encoding Genetic Algorithm in Solving the Multiple Traveling salesmen Problem. In Proceedings of the International Conference on Technologies and Applications of Artificial Intelligence, Chung Li, Taiwan, 11–13 November 2011.
  62. Király, A.; Abonyi, J. Optimization of Multiple Traveling salesmen Problem by a Novel Representation Based Genetic Algorithm. In Intelligent Computational Optimization in Engineering. Studies in Computational Intelligence; Köppen, M., Schaefer, G., Abraham, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 366, pp. 241–269. ISBN 978-3-642-21704-3.
  63. Sedighpour, M.; Yousefikhoshbakht, M.; Darani, N.M. An Effective Genetic Algorithm for Solving the Multiple Traveling salesman Problem. J. Optim. Ind. Eng. 2011, 8, 73–79.
  64. Yu, Q.; Wang, D.; Lin, D.; Li, Y.; Wu, C. A Novel Two-Level Hybrid Algorithm for Multiple Traveling Salesman Problems. In Advances in Swarm Intelligence. ICSI 2012. Lecture Notes in Computer Science; Tan, Y., Shi, Y., Ji, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7331, pp. 497–503. ISBN 978-3-642-30975-5.
  65. Yuan, S.; Skinner, B.; Huang, S.; Liu, L. A new crossover approach for solving the multiple travelling salesmen problem using genetic algorithms. Eur. J. Oper. Res. 2013, 228, 72–82.
  66. Hosseinabadi, A.A.R.; Kardgar, M.; Shojafar, M.; Shamshirband, S.; Abraham, A. GELS-GA: Hybrid metaheuristic algorithm for solving Multiple Travelling salesman Problem. In Proceedings of the 14th International Conference on Intelligent Systems Design and Applications, Okinawa, Japan, 28–30 November 2014.
  67. Alves, R.M.F.; Lopes, C.R. Using genetic algorithms to minimize the distance and balance the routes for the multiple Traveling salesman Problem. In Proceedings of the IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015.
  68. Bolaños, R.I.; Toro, E.M.; Granada, M. A population-based algorithm for the multi travelling salesman problem. Int. J. Ind. Eng. Comput. 2016, 7, 245–256.
  69. Lu, Z.; Zhang, K.; He, J.; Niu, Y. Applying K-means Clustering and Genetic Algorithm for Solving MTSP. In Proceedings of the 11th International Conference, BIC-TA, Xi’an, China, 28–30 October 2016.
  70. Lo, K.M.; Yi, W.Y.; Wong, P.K.; Leung, K.S.; Leung, Y.; Mak, S.T. A Genetic Algorithm with New Local Operators for Multiple Traveling salesman Problems. Int. J. Comput. Intell. Syst. 2018, 11, 692–705.
  71. Singh, D.R.; Singh, M.K.; Singh, T.; Prasad, R. Genetic Algorithm for Solving Multiple Traveling Salesmen Problem using a New Crossover and Population Generation. Comput. Sist. 2018, 22, 491–503.
  72. Xu, X.; Yuan, H.; Liptrott, M.; Trovati, M. Two phase heuristic algorithm for the multiple-travelling salesman problem. Soft Comput. 2018, 22, 6567–6581.
  73. Zhou, H.; Song, M.; Pedrycz, W. A comparative study of improved GA and PSO in solving multiple traveling salesmen problem. Appl. Soft Comput. 2018, 64, 564–580.
  74. Harrath, Y.; Salman, A.F.; Alqaddoumi, A.; Hasan, H.; Radhi, A. A novel hybrid approach for solving the multiple traveling salesmen problem. Arab. J. Basic Appl. Sci. 2019, 26, 103–112.
  75. Jiang, C.; Wan, Z.; Peng, Z. A new efficient hybrid algorithm for large scale multiple traveling salesman problems. Expert Syst. Appl. 2020, 139, 112867.
  76. Al-Furhud, M.A.; Ahmed, Z.H. Experimental Study of a Hybrid Genetic Algorithm for the Multiple Travelling salesman Problem. Math. Probl. Eng. 2020, 2020, 3431420.
  77. Wang, Z.; Fang, X.; Li, H.; Jin, H. An Improved Partheno-Genetic Algorithm With Reproduction Mechanism for the Multiple Traveling Salesperson Problem. IEEE Access 2020, 8, 102607–102615.
  78. Singamsetty, P.; Thenepalle, J.K. An efficient genetic algorithm for solving open multiple travelling salesman problem with load balancing constraint. Decis. Sci. Lett. 2021, 10, 525–534.
  79. Al-Taani, A.T.; Al-Alfifi, L.M. Solving the Multiple Traveling Salesman Problem Using Memetic Algorithm. Artif. Intell. Evol. 2022, 3, 27–40.
  80. Lou, P.; Xu, K.; Yan, J.; Xiao, Z. An Improved Partheno-Genetic Algorithm for Open Path Multi-Depot Multiple Traveling Salesmen Problem. J. Phys. Conf. Ser. 2021, 1848, 012002.
  81. Chandran, N.; Narendran, T.T.; Ganesh, K. A clustering approach to solve the multiple travelling salesmen problem. Int. J. Ind. Syst. Eng. 2006, 1, 372–387.
  82. Junjie, P.; Dingwei, W.; Preucil, L. An Ant Colony Optimization Algorithm for Multiple Travelling salesman Problem. In Proceedings of the First International Conference on Innovative Computing, Beijing, China, 30 August–1 September 2006.
  83. Liu, W.; Li, S.; Zhao, F.; Zheng, A. An ant colony optimization algorithm for the Multiple Traveling Salesmen Problem. In Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009.
  84. Ghafurian, S.; Javadian, N. An ant colony algorithm for solving fixed destination multi-depot multiple traveling salesmen problems. Appl. Soft Comput. 2011, 11, 1256–1262.
  85. Yousefikhoshbakht, M.; Sedighpour, M. A combination of sweep algorithm and elite ant colony optimization for solving the multiple traveling salesman problem. Proc. Rom. Acad. -Ser. Math. Physics, Tech. Sci. Inf. Sci. 2012, 13, 295–301.
  86. Lu, L.C.; Yue, T.W. Mission-oriented ant-team ACO for min–max MTSP. Appl. Soft Comput. 2019, 76, 436–444.
  87. Farisi, O.I.R.; Setiyono, B.; Danandjojo, R.I. A hybrid approach to multi-depot multiple traveling salesman problem based on firefly algorithm and ant colony optimization. Int. J. Artif. Intell. (IJ-AI) 2021, 10, 910–918.
  88. Costa-Salas, Y.J.; Abreu-Ledón, R.; Coello-Machado, J.I.; Nowé, A. Multi-type ant colony system for solving the multiple traveling salesman problem. Rev. TéCnica Fac. Ing. Univ. Del Zulia 2012, 35, 311–320.
  89. Necula, R.; Breaban, M.; Raschip, M. Performance Evaluation of Ant Colony Systems for the Single-Depot Multiple Traveling Salesman Problem. In Hybrid Artificial Intelligent Systems; Onieva, E., Santos, I., Osaba, E., Quintián, H., Corchado, E., Eds.; Springer: Cham, Switzerland, 2015; Volume 9121, pp. 257–268. ISBN 978-3-319-19643-5.
  90. Kivelevitch, E.; Cohen, K.; Kumar, M. A Market-based Solution to the Multiple Traveling salesmen Problem. J. Intell. Robot. Syst. 2013, 72, 21–40.
  91. Scott, D.; Manyam, S.G.; Casbeer, D.W.; Kumar, M. Market Approach to Length Constrained Min-Max Multiple Depot Multiple Traveling Salesman Problem. In Proceedings of the 2020 American Control Conference, Denver, CO, USA, 1–3 July 2020.
  92. Larki, H.; Yousefikhoshbakht, M. Solving the Multiple Traveling salesman Problem by a Novel Meta-heuristic Algorithm. J. Optim. Ind. Eng. 2014, 16, 55–63.
  93. Rostami, A.S.; Mohanna, F.; Keshavarz, H.; Hosseinabadi, A.A.R. Solving Multiple Traveling Salesman Problem using the Gravitational Emulation Local Search Algorithm. Appl. Math. Inf. Sci. 2015, 2, 699–709.
  94. Soylu, B. A general variable neighborhood search heuristic for multiple traveling salesmen problem. Comput. Ind. Eng. 2015, 90, 390–401.
  95. Wang, Y.; Chen, Y.; Lin, Y. Memetic algorithm based on sequential variable neighborhood descent for the minmax multiple traveling salesman problem. Comput. Ind. Eng. 2017, 106, 105–122.
  96. Dong, X.; Zhang, H.; Xu, M.; Shen, F. Hybrid genetic algorithm with variable neighborhood search for multi-scale multiple bottleneck traveling salesmen problem. Future Gener. Comput. Syst. 2021, 114, 229–242.
  97. Wang, M.; Xin, B.; Wang, Q. A general variable neighborhood search for the multiple depots multiple traveling salesmen problem. In Proceedings of the The International Workshop on Advanced Computational Intelligence and Intelligent Informatics (IWACIII2021), Beijing, China, 31 October–3 November 2021.
  98. Venkatesh, P.; Singh, A. Two metaheuristic approaches for the multiple traveling salesperson problem. Appl. Soft Comput. 2015, 26, 74–89.
  99. Chen, Y.; Jia, Z.; Ai, X.; Yang, D.; Yu, J. A modified two-part wolf pack search algorithm for the multiple traveling salesmen problem. Appl. Soft Comput. 2017, 61, 714–725.
  100. Alazzam, H.; Alsmady, A.; Mardini, W. Solving Multiple Traveling salesmen Problem using Discrete Pigeon Inspired Optimizer. In Proceedings of the 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020.
  101. Hu, Y.; Yao, Y.; Lee, W.S. A reinforcement learning approach for optimizing multiple traveling salesman problems over graphs. Knowl.-Based Syst. 2020, 204, 106244.
  102. Karabulut, K.; Öztop, H.; Kandiller, L.; Tasgetiren, M.F. Modeling and optimization of multiple traveling salesmen problems: An evolution strategy approach. Comput. Oper. Res. 2021, 129, 105192.
  103. He, P.; Hao, J.-K. Memetic search for the minmax multiple traveling salesman problem with single and multiple depots. Eur. J. Oper. Res. 2023, 307, 1055–1070.
  104. Zhang, Y.; Han, X.; Dong, Y.; Xie, J.; Xie, G.; Xu, X. A novel state transition simulated annealing algorithm for the multiple traveling salesmen problem. J. Supercomput. 2021, 77, 11827–11852.
  105. Hamza, A.; Darwish, A.H.; Rihawi, O. A new local search for the bees algorithm to optimize multiple traveling salesman problem. Intell. Syst. Appl. 2023, 18, 200242.
  106. Averbakh, I.; Berman, O. A heuristic with worst-case analysis for minimax routing of two travelling salesmen on a tree. Discret. Appl. Math. 1996, 68, 17–32.
  107. Averbakh, I.; Berman, O. (p-1)(p+1)-approximate algorithms for p-traveling salesmen problems on a tree with minmax objective. Discret. Appl. Math. 1997, 75, 201–216.
  108. Nagamoshi, H.; Okada, K. A faster 2-approximation algorithm for the minmax p-traveling salesmen problem on a tree. Discret. Appl. Math. 2004, 140, 103–114.
  109. Rathinam, S.; Sengupta, R. Lower and Upper Bounds for a Symmetric Multiple Depots, Multiple Travelling salesman Problem; Research Report, UCB-ITS-RR-2006-2; Institute of Transportation Studies, University of California at Berkeley: Berkeley, CA, USA, 2006.
  110. Xu, Z.; Rodrigues, B. A 3/2-Approximation Algorithm for Multiple Depot Multiple Traveling salesman Problem. In Lecture Notes in Computer Science; Kaplan, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6139, pp. 127–138. ISBN 978-3-642-13730-3.
  111. Xu, Z.; Xu, L.; Rodrigues, B. An analysis of the extended Christofides heuristic for the k-depot TSP. Oper. Res. Lett. 2011, 39, 218–223.
  112. Xu, Z.; Rodrigues, B. An extension of the Christofides heuristic for the generalized multiple depot multiple traveling salesmen problem. Eur. J. Oper. Res. 2017, 257, 735–745.
  113. Xu, L.; Xu, Z.; Xu, D. Exact and approximation algorithms for the min–max k-traveling salesmen problem on a tree. Eur. J. Oper. Res. 2013, 227, 284–292.
  114. Pérez-Escalona, P.; Rapaport, I.; Soto, J.; Vidal, I. The Multiple Traveling Salesman Problem on Spiders. In Proceedings of the 47th International Conference on Current Trends in Theory and Practice of Computer Science, SOFSEM, Bolzano-Bozen, Italy, 25–29 January 2021.
  115. He, P.; Hao, J.-K. Hybrid search with neighborhood reduction for the multiple traveling salesman problem. Comput. Oper. Res. 2022, 142, 105726.
  116. Mantha, B.R.K.; Jung, M.K.; García de Soto, B.; Menassa, C.C.; Kamat, V.R. Generalized task allocation and route planning for robots with multiple depots in indoor building environments. Autom. Constr. 2020, 119, 103359.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback