Cardiovascular diseases (CVDs), including asymptomatic myocardial ischemia, angina, myocardial infarction, and ischemic heart failure, are the leading cause of death globally. Early detection and treatment of CVDs significantly contribute to the prevention or delay of cardiovascular death. Electrocardiogram (ECG) records the electrical impulses generated by heart muscles, which reflect regular or irregular beating activity. Computer-aided techniques provide fast and accurate tools to identify CVDs using a patient’s ECG signal, which have achieved great success in recent years. Latest computational diagnostic techniques based on ECG signals for estimating CVDs conditions are summarized here. The procedure of ECG signals analysis is discussed in several subsections, including data preprocessing, feature engineering, classification, and application. In particular, the End-to-End models integrate feature extraction and classification into learning algorithms, which not only greatly simplifies the process of data analysis, but also shows excellent accuracy and robustness. Portable devices enable users to monitor their cardiovascular status at any time, bringing new scenarios as well as challenges to the application of ECG algorithms. Computational diagnostic techniques for ECG signal analysis show great potential for helping health care professionals, and their application in daily life benefits both patients and sub-healthy people.
- electrocardiogram
- classification
- feature engineering
- deep learning
- machine learning
1. Introduction
ECG reflects the regular or irregular beating activity of heart because it records electrical impulses generated by heart muscles. Therefore, it is crucial to extract as much meaningful clinical information as possible from ECG signals. Doctors often make diagnoses by observing the morphological characteristics of P-QRS-T waves, which largely depends on doctors’ experience and usually takes a long time. Computer-aided analysis based on feature engineering has greatly improved the efficiency and accuracy in ECG analysis. ECG signals consisting of abundant data points can be extracted a small number of features in terms of its peak amplitude, morphology, energy and entropy distribution, frequency content, intervals between events, which can represent the behavior of the ECG signal. These features commonly applied to ECG diagnosis include P-QRS-T features, statistical features, morphological features, frequency-domain features and other more complex parameters, which provide effective tools for doctors’ judgment. Advanced algorithms extract features according to the needs of the task and automatically selects specific features to achieve precise diagnosis. As the core of ECG analysis, feature extraction and selection play a decisive role in the performance of the algorithm.
2. Features for Disease Diagnosis
2.1. P-QRS-T Complex Feature
ECG waveform reflects the activity of heart tissue, which is a very weak physiological low-frequency electrical signal. The maximum amplitude is no more than 5 mv and signal frequency is in the ranges from 0.05–100 Hz. Normal ECG waveform consists of P-wave, QRS complex, T-wave and sometimes U waves (Figure 2). Morphological features of ECG signal include different peak amplitudes, peak intervals and QRS complex, etc. The typical morphological features of ECG signal are summarized in Table 1. Sinoatrial node (SA) depolarization occurs before the depolarization of atrial myocytes, so it is before P-waveform. But SA is inside the heart, and its electrical activity is difficult to be collected on the body surface. The excitement of the SA is transmitted to the right atrium, and then to the left atrium via the ventricular tract, forming a P-wave which represents the excitement of the two atria. P-waveform is relatively small, with a round shape, an amplitude of about 0.25 mV and a length of 0.08~0.11 s. When atrial enlargement occurs, the conduction between the two atria will be abnormal, resulting in P-mitrale or P-pulmonale waves. P-R interval refers to the interval from the onset of P wave to the beginning of QRS complex on an ECG signal. In normal ECG, P-R interval is 0.12–0.2 s, which corresponds with the spread of the electrical conduction in atrioventricular junction. A prolonged P-R interval reflects impaired atrial conduction, and maybe an indicator of ischemic strokes[1]. The QRS complex represents the spread of a stimulus through the ventricles. A complete QRS complex consists of Q-, R- and S-wave. R wave is long and narrow, representing the depolarization of the left ventricle apex[2]. The typical duration of QRS complex is about 0.06–0.1 s. Heart rate is usually measured by recording the number of QRS complexes in a minute. The comprehensive electric field vector of ventricular myocytes changes many times in the process of excitation, which forms the signal with multiple changes in size and direction. When the conduction block of the left and right bundle branches of the heart, ventricular enlargement or hypertrophy occurs, the QRS complex will widen, deform and prolong. T wave follows QRS complex, and is produced by repolarization of ventricular myocytes with an amplitude of 0.1–0.8 mV and lasts for 0.05–0.25 s. The T wave is always positive and is useful for the diagnosis of certain cardiovascular diseases. It’s common to detect abnormal T waves (e.g., inverted T waves) by chest leads on patients with pulmonary embolism (PE). Marcinkevics. R. et al. found that the T-wave amplitude of patients with arrhythmia right ventricular dysplasia (ARVD) was significantly different from that of normal patients[3]. U-wave is the last unsteady and smallest wave in the ECG, which shows a circular upward deflection. Sometimes, U-wave may not be observed because of its small size. The formation of U wave is controversial. Generally, U-wave is thought to represent repolarization of the Purkinje fibers. Usually, U wave has the same polarity as T wave. In clinical diagnosis, transient U-wave inversion can be caused by local myocardial ischemia or hypertension[4].
Table 1. ECG features and the normal values for a healthy adult.
|
Features |
Description |
Amplitude |
Duration |
Disease diagnosis |
Reference |
|
R-R interval |
The interval between two successive R-waves of the QRS complex ventricular rate |
|
0.6–1.2 s |
Paroxysmal atrial fibrillation Congestive heart failure |
|
|
P wave |
Atrial depolarization |
0.25 mV |
0.08–0.11 s |
Atrial fibrillation Atrial hypertrophy |
[7] |
|
P-R interval |
The time between the onset of atrial depolarization and the onset of ventricular depolarization |
|
0.12–0.2 s |
Stroke |
[1] |
|
QRS complex |
Ventricular depolarization |
1.60 mV for R peak |
0.06–0.1 s |
Ventricular enlargement Heart failure Tachycardia Acute Coronary Syndrome |
|
|
ST-segment |
The interval between ventricular depolarization and repolarization |
|
0.05–0.155 s |
Myocardial ischemia or infarction |
[11] |
|
T wave |
Ventricular repolarization |
0.1–0.8 mV
|
0.05–0.25 s |
Myocardial infarction Pulmonary embolism |
|
|
U wave |
The last phase of ventricular repolarization |
May not be observed because of its small size |
Unknown |
Unknown |
[4] |
|
QT interval |
The time is taken for ventricular depolarisation and repolarisation |
|
0.35–0.44 s |
Hypokalemia ventricular arrhythmias |
[14] |
Figure 2. Cardiac electrical conduction system and the electrocardiogram signal.
Segments and intervals of the ECG signal reflect each stage and cardiac cycle of heart contraction, which should be completed within a specific period for a healthy person. The abnormal period indicates something wrong with the heart[15]. R-R interval is the time elapsed between two consecutive R waves of the QRS signal. It is usually employed to assess ventricular rate. During sinus rhythm, patients with short-term risk of paroxysmal atrial fibrillation (PAF) tend to show higher RR interval variability[5]. Q-T interval refers to the time from the beginning of QRS to the end of T wave, representing the total time required for ventricular depolarization and repolarization. It is worth noticing that P-R interval is different from the P-R segment, which is the time between the end of the P-wave and the beginning of the QRS wave. The P-R interval reflects the time delay between atrial and ventricular activation, which indicates whether impulse conduction from the atria to the ventricles is normal. The proper feature selection of ECG waveform can be used in some specific disease diagnosis. S-T segment refers to the period between the end of QRS complex and the start of T wave. During the S-T segment, the myocytes of the left and right ventricles are in the excitation period, so the contribution of the combined electric field vector formed by the two is very small in the body surface ECG, and the signal in S-T segment is at the baseline level. When a segment of myocardium is ischemic or necrotic, the ventricular potential difference still exists after the completion of depolarization, which is manifested as S-T segment shift on the ECG waveform[11]. The typical disease that is associated with S-T segment is the myocardial infarction (MI), which is commonly known as a heart attack, occurs when the blood supply to the portion of the heart is blocked, causing some heart cells to die. The corresponding ECG signal is depicted in the elevated ST segment, increased Q wave amplitude and inverted T wave.
3. Dimensionality Reduction
High dimensionality of the feature space can provide much more detailed information of ECG signal. However, the higher the number of data, the more computational cost. Some of the features may be correlated, resulting in a large number of irrelevant variables, which will significantly affect computational efficiency due to the large redundant data[16]. Hence, it is vital to remove some correlated features while improving the accuracy and efficiency of classification. Dimensionality reduction makes data analysis much simple and fast, thus improving the performance of clustering algorithms with reduced features. Usually, the dimensionality reduction is accomplished based on either feature selection or feature extraction.
2.1. Feature selection
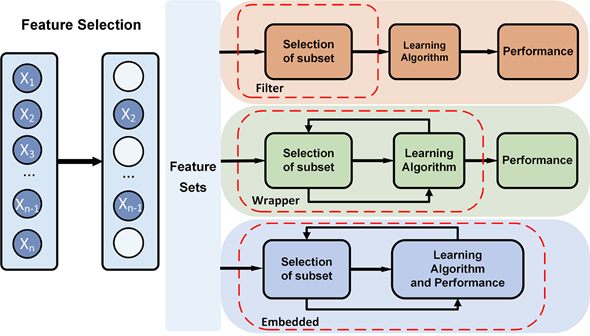
Feature selection tries to select a subset of the original feature set, which efficiently describes the input data and makes weak correlation among these features[17]. Therefore, the focus of feature selection is to find appropriate standards or algorithms to evaluate the contribution of features to the results, thus reducing the dimension of features for improving the model generalization ability and reducing overfitting. Feature selection usually involves three ways, including filters, wrappers and embedded (Figure 3).
Filter-based feature selection applies a selected metric to find irrelevant attributes and filters out the redundant data[95]. The selection process is independent of the training process. Filter-based methods rank the features as a pre-processing step before the learning algorithm, and select those features with high ranking scores. The score is computed by measuring the variance between the expected value of the information and the observed value. The evaluation metric of filter usually is used to analyze the internal features of the feature subset, which includes correlation, distance, information gain, and so on. In practice, filter-based feature selection can be initially screened by expert knowledge, then filtered by filtering methods. The characteristics that have been proven to be relevant to a particular disease or physiological response are often directly selected in feature selection. Besides, it is a common method to calculate a score for each feature column. Columns with poor feature selection scores are ignored. Filter-based feature selection provides a variety of performance criteria for assessing the information value, such as correlation coefficient, mutual information, Kendall correlation, Spearman correlation, Chi Squared, Fisher score, Laplacian score, Trace Ratio criterion, among which, Fisher score is widely used metrics for supervised feature selection. Fahim Sufi et al. ranked feature subsets according to a correlation-based heuristic evaluation function[18]. The algorithm selected features by calculating mean feature-class correlation and the average feature-feature intercorrelation. The two criteria ensure that irrelevant features and redundant features are removed from the attributes set, because they are not correlated with the class or other features. Some researchers evaluated each feature from the primary feature sets by Fisher score[19][20]. The fisher score selected each ECG feature independently according to their scores under the Fisher criterion, resulting in suboptimal subset of attributes. It is often used to select feature sets with lower dimension. The Filter method uses statistical indicators to score and filter each feature, focusing on the characteristics of the data itself. The advantage of the Filter method is that the calculation is fast and does not depend on a specific model. However, the final accuracy of the classification may be not high because the selected features are not customized for the specific model
Wrapper-based feature selection utilizes a predefined classifier to evaluate the feature set. This method scores the features using the learning algorithm that will ultimately be employed in classification. The feature selection process is integrated with training process, and the prediction ability of the model is used as the selection criterion to evaluate the feature subset, such as classification accuracy, complexity penalty factor. Forward and backward selection algorithm in multiple linear regression is a simple implementation of wrapper. Sequential floating forward search (SFFS) algorithm utilizes sequential forward selection (SFS) and sequential backward selection (SBS) in sequence to obtain the best ECG feature set. Llamedo and Martinez obtained an optimal ECG feature set containing eight features by SFFS[21]. The SFFS method is suitable for small-and medium-scale data [22]. KNN[23] and SVM[24] can be used as evaluation functions of the wrapper. Compared with the filter, the wrapper has better performance in generating high-quality subsets, but the data processing is computationally expensive since the learner needs to be trained many times during the feature selection process. Unlike filter selection, which does not consider subsequent classification algorithms, wrapped selection directly takes the performance of the final classification algorithms as the evaluation standard of the feature subset. In other words, wrapped feature selection is to select the most favorable feature subset for a given learning algorithm. However, the performance of the subset of features is affected by the particular learning algorithm. The stability and adaptability of the feature subset are poor because each additional feature must be constructed feature subset for evaluation. Wrapper-based feature selection has high time complexity and is not suitable for high dimensional data set.
Embedded feature selection is built into the construction of the machine learning algorithm. It provides a trade-off solution between filter method and wrapper method, which can solve the high redundancy of the filter algorithm and the computational complexity of the wrapper algorithm. The embedded feature selection is automatically performed during the learner training process[18]. Compared to the other two methods, the searching and selection process of features’ subset is built into classifier construction. Regularization and tree-based methods are widely used in embedded methods. The regularization models in form of ℓ2, 1-norm regularized regression models, such as Lasso, sparse linear discriminant analysis, and regularized support vector machine, are widely used in embedded methods[25]. Regularization is to impose additional constraints or penalties on the loss function when training a neural network, which can reduce the complexity and instability of the model in the learning process, thus avoiding overfitting and improving generalization ability. Decision tree is a classic embedded feature selection method, such as ID3, C4.5, CART algorithm. Features with good ability of classification are selected in the nodes of the tree, and then the selected feature subsets are used to perform the learning tasks. Feature subsets are selected during the process of decision tree generation. The random forest has the advantages of high accuracy, good robustness and easy to use, which makes it one of the most popular machine learning algorithms. The random forest provides two methods of feature selection, including mean decrease impurity and mean decrease accuracy. Tree-based prediction models can be used to calculate the importance of features, and thus to remove irrelevant features. Embedded feature selection can be applied to high dimensional data sets, but the design of the embedded method is tightly coupled with a specific learning algorithm, which in turn limits its application to other learning algorithms.
Figure 3. Feature selection methods, such as filter, wrapper, and embedded method.
Feature Extraction
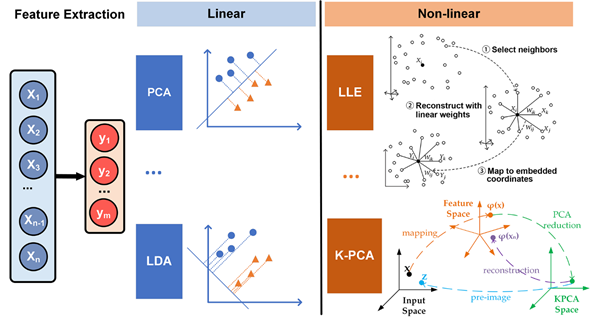
The disadvantage of feature selection is that unselected features are simply moved out, which will reduce the accuracy and efficiency of learning algorithms. Feature extraction considers all features and maps the useful information into a low-dimensional feature space, which is more commonly used in the selection of feature sets with insufficient prior knowledge and high-dimensionality. By choosing an appropriate dimension reduction method, the invalid information of the original feature set can be removed and the effective information of the original feature set is retained to the greatest extent. Typical dimensionality reduction methods include principal component analysis (PCA), linear discriminant analysis (LDA), independent component analysis (ICA), and generalized discriminant analysis (GDA)[26].
The PCA method is a linear dimensionality reduction method that maps the original features into a low-dimensional space while retaining the variance. PCA is the most widely used form of dimensionality reduction, which preserves the maximum amount of variance of the original data. The choice of optimal number of principal components is one of the major challenges for providing meaningful interpretation of time series. He and Tan developed entropy-based adaptive dimensionality reduction and clustering methods for automatic pattern recognition of ECG signals[27]. A novel entropy-based principal component analysis (EPCA) was developed to automatically select the optimal number of principal components for dimensionality reduction of ECG signals. Then, a novel fuzzy entropy c-means clustering algorithm (FECM) was utilized to identify the best number of clusters for a specific subject. The results on ECG signals verify that the performance of EPCA is superior to PCA based on cumulative percentage and screen graph. The clustering accuracy of FECM performs superiorly to Ng–Jordan–Weiss (NJW) method, hierarchical agglomerative clustering (HAC) and K-means with the known cluster number. LDA also known as Fisher’s discriminant analysis, is a dimensionality reduction algorithm. Unlike PCA, LDA is a supervised algorithm that maximizes separation between multiple classes, while PCA is an unsupervised algorithm that focusses on maximizing variance in a dataset. PDA shows good performance in pattern recognition. Varatharajan et al. applied LDA to reduce the features of the ECG signal[28]. The effectiveness of LDA with an enhanced kernel-based SVM method was proved by calculation of sensitivity, specificity and mean square error. LDA is applied to DWT sub-bands for dimensionality reduction by Martis et al.[29]. By using 12 linear discriminant features as input, both neural network and SVM achieved average classification accuracy of more than 97%. ICA is a linear dimension reduction method, which transforms the features into columns of mutually independent components[30][31]. Independent components can be picked up from the mixed signals by ICA. Martis et al. compared the performance of various dimensionality reduction techniques for arrhythmia classification, including PCA, LDA and ICA, based on DWT features[32]. ICA coupled with neural network yielded the highest average sensitivity, specificity, and accuracy of 99.97%, 99.83% and 99.28%, respectively. Experimental results showed that the ICA on DWT coefficients was more robust and yielded good classification accuracy. The linear feature extraction methods are relatively simple, however, the feature extraction model will be wrong by projecting data onto a linear subspace when the dataset has non-linear connections.
In clinical practice, all the changes of ECG parameters are detected by visual evaluation and manual interpretation to detect the presence of cardiovascular disease. However, due to the nonstationary and nonlinear nature of ECG signals, cardiovascular disease indicators may appear randomly on the time scale. Non-linear features of ECG, such as energy (Ee), entropy (Ez), fractal dimension (FD), and relative wavelet (RWz) can be extracted to show some diagnostic details that can’t be simply detected by visual evaluation[33]. Nonlinear methods can perform better in complex nonlinear relationships among the features[34]. Locally linear embedding (LLE) is an unsupervised nonlinear dimensionality reduction method, which tries to preserve the data structure by a non-linear method according to local features of the dataset (Figure 4).
Figure 4. Different feature extraction methods used in ECG analysis.
It can perform much faster than the other approaches. However, LLE is extremely susceptive to noises, and LLE will not preserve well the local geometry of the data sets in the embedding space if there are outliers in the data[35]. Kernel-based method has become one of the most popular approaches to extract the complicated nonlinear information embedded on an ECG dataset. Kernel LLE (KLLE) can reconstruct nonlinear data as a linear combination of its neighbors. Li et al. mapped 12-dimensional features of ECG segments of single beat type into 7-dimensional embedding space described by two coordinates of kernel LLE[36]. The results showed that the true/false ratio for the proposed method outperformed other selected methods. The KLLE space shows better performance in loss of diagnostic information in ECG signals. Kernel principal component analysis (KPCA) is a popular nonlinear generalization of PCA, which is suitable for processing linearly nonseparable data sets. The basic idea of KPCA is to map the original data into a high dimensional space via a kernel function ( ), and then to apply the standard PCA algorithm to it (Figure 4)[37], which can extract a more complete nonlinear representation of the principal components. However, KPCA takes more time than PCA.
This entry is adapted from the peer-reviewed paper 10.3390/s20216318
References
- Montalvo, M.; Tadi, P.; Merkler, A.; Gialdini, G.; Martin-Schild, S.; Navalkele, D.; Samai, A.; Nouh, A.; Hussain, M.; Goldblatt, S.; et al. PR Interval Prolongation and Cryptogenic Stroke: A Multicenter Retrospective Study. J. Stroke Cerebrovasc. Dis. 2017, 26, 2416–2420.
- Merone, M.; Soda, P.; Sansone, M.; Sansone, C. ECG databases for biometric systems: A systematic review. Expert Syst. Appl. 2017, 67, 189–202.
- Marcinkevics, R.; O.; Neill, J.; Law, H.; Pervolaraki, E.; Hogarth, A.; Russell, C.; Stegemann, B.; Holden, A.V.; Tayebjee, M.H. Multichannel electrocardiogram diagnostics for the diagnosis of arrhythmogenic right ventricular dysplasia. EP Eur. 2018, 20, f13–f19.
- Pérez-Riera, A.; Ferreira, C.; Filho, C.; Ferreira, M.; Meneghini, A.; Uchida, A.; Schapachnik, E.; Dubner, S.; Zhang, L. The enigmatic sixth wave of the electrocardiogram: The U wave. Cardiol. J. 2008, 15, 408–421.
- Adami, A.; Gentile, C.; Hepp, T.; Molon, G.; Gigli, G.L.; Valente, M.; Thijs, V. Electrocardiographic RR Interval Dynamic Analysis to Identify Acute Stroke Patients at High Risk for Atrial Fibrillation Episodes During Stroke Unit Admission. Transl. Stroke Res. 2019, 10, 273–278.
- Liu, C.; Gao, R. Multiscale Entropy Analysis of the Differential RR Interval Time Series Signal and Its Application in Detecting Congestive Heart Failure. Entropy 2017, 19, 251.
- Pürerfellner, H.; Pokushalov, E.; Sarkar, S.; Koehler, J.; Zhou, R.; Urban, L.; Hindricks, G. P-wave evidence as a method for improving algorithm to detect atrial fibrillation in insertable cardiac monitors. Heart Rhythm 2014, 11, 1575–1583.
- Bax, J.J.; Delgado, V.; Sogaard, P.; Singh, J.P.; Abraham, W.T.; Borer, J.S.; Dickstein, K.; Gras, D.; Brugada, J.; Robertson, M.; et al. Prognostic implications of left ventricular global longitudinal strain in heart failure patients with narrow QRS complex treated with cardiac resynchronization therapy: a subanalysis of the randomized EchoCRT trial. Eur. Heart J. 2016, 38, 720–726.
- Brady, W.J.; Mattu, A.; Tabas, J.; Ferguson, J.D. The differential diagnosis of wide QRS complex tachycardia. Am. J. Emerg. Med. 2017, 35, 1525–1529.
- Ibrahim Radwan, H.; Saad Mansour, K.; Mustafa Al-Daydamony, M.; Saed Mohammed, R. Fragmented QRS Complex as a Predictor of High Risk in Acute Coronary Syndrome. Cardiol. Cardiovasc. Res. 2019, 3, 71.
- Hausenloy, D.J.; Botker, H.E.; Engstrom, T.; Erlinge, D.; Heusch, G.; Ibanez, B.; Kloner, R.A.; Ovize, M.; Yellon, D.M.; Garcia-Dorado, D. Targeting reperfusion injury in patients with ST-segment elevation myocardial infarction: trials and tribulations. Eur. Heart J. 2016, 38, 935–941.
- Onur, I.; Emet, S.; Onur, S.T.; Kara, K.; Surmen, S.; Bilge, A.K.; Adalet, K. PM299 A Novel Parameter for the Diagnosis of Acute Pulmonary Embolism: T Wave Peak to End Interval. Glob. Heart 2016, 11, e121–e122.
- Nakagawa, T.; Yagi, T.; Ishida, A.; Mibiki, Y.; Yamashina, Y.; Sato, H.; Sato, E.; Komatsu, J.; Saijo, Y. Differences between cardiac memory T wave changes after idiopathic left ventricular tachycardia and ischemic T wave inversion induced by acute coronary syndrome. J. Electrocardiol. 2016, 49, 596–602.
- Hermans, B.J.M.; Bennis, F.C.; Vink, A.S.; Koopsen, T.; Lyon, A.; Wilde, A.A.M.; Nuyens, D.; Robyns, T.; Pison, L.; Postema, P.G.; et al. Improving long QT syndrome diagnosis by a polynomial-based T-wave morphology characterization. Heart Rhythm 2020, 17, 752–758.
- DeChazal, P.; O’Dwyer, M.; Reilly, R.B. Automatic Classification of Heartbeats Using ECG Morphology and Heartbeat Interval Features. IEEE T. Biomed. Eng. 2004, 51, 1196–1206.
- Qin, Q.; Li, J.; Zhang, L.; Yue, Y.; Liu, C. Combining Low-dimensional Wavelet Features and Support Vector Machine for Arrhythmia Beat Classification. Sci Rep. UK 2017, 7, 1–12.
- Blum, A.L.; Langley, P. Selection of relevant features and examples in machine learning. Artif. Intell. 1997, 97, 245–271.
- Sufi, F.; Khalil, I. Faster person identification using compressed ECG in time critical wireless telecardiology applications. J. Netw. Comput. Appl. 2011, 34, 282–293.
- Khalaf, A.F.; Owis, M.I.; Yassine, I.A. A novel technique for cardiac arrhythmia classification using spectral correlation and support vector machines. Expert Syst. Appl. 2015, 42, 8361–8368.
- Yu, S.; Chen, Y. Noise-tolerant electrocardiogram beat classification based on higher order statistics of subband components. Artif. Intell. Med. 2009, 46, 165–178.
- Llamedo, M.; Martínez, J.P. Heartbeat Classification Using Feature Selection Driven by Database Generalization Criteria. IEEE T. Biomed. Eng. 2011, 58, 616–625.
- Kudo, M.; Sklansky, J. Comparison of algorithms that select features for pattern classifiers. Pattern Recogn. 2000, 33, 25–41.
- Wang, A.; An, N.; Chen, G.; Li, L.; Alterovitz, G. Accelerating wrapper-based feature selection with K-nearest-neighbor. Knowl. Based Syst. 2015, 83, 81–91.
- Song, C.; Liu, K.; Zhang, X.; Chen, L.; Xian, X. An Obstructive Sleep Apnea Detection Approach Using a Discriminative Hidden Markov Model From ECG Signals. IEEE T. Biomed. Eng. 2016, 63, 1532–1542.
- Lu, M. Embedded feature selection accounting for unknown data heterogeneity. Exp. Syst. Appl. 2019, 119, 350–361.
- Ye, C.; Kumar, B.V.; Coimbra, M.T. Heartbeat classification using morphological and dynamic features of ECG signals. IEEE Trans. Biomed. Eng. 2012, 59, 2930–2941.
- He, H.; Tan, Y. Automatic pattern recognition of ECG signals using entropy-based adaptive dimensionality reduction and clustering. Appl. Soft Comput. 2017, 55, 238–252.
- Varatharajan, R.; Manogaran, G.; Priyan, M.K. A big data classification approach using LDA with an enhanced SVM method for ECG signals in cloud computing. Multimed. Tools Appl. 2018, 77, 10195–10215.
- Martis, R.J.; Acharya, U.R.; Min, L.C. ECG beat classification using PCA, LDA, ICA and Discrete Wavelet Transform. Biomed. Signal Proces. 2013, 8, 437–448.
- Bollmann, A.; Kanuru, N.; McTeague, K.; Walter, P.; DeLurgio, D.; Langberg, J. Frequency Analysis of Human Atrial Fibrillation Using the Surface Electrocardiogram and Its Response to Ibutilide. Am. J. Cardiol. 1998, 81, 1439–1445.
- Rieta, J.J.; Castells, F.; Sanchez, C.; Zarzoso, V.; Millet, J. Atrial Activity Extraction for Atrial Fibrillation Analysis Using Blind Source Separation.IEEE T. Biomed. Eng. 2004, 51, 1176–1186.
- Liu, J.; Zhang, C.; Zhu, Y.; Ristaniemi, T.; Parviainen, T.; Cong, F. Automated detection and localization system of myocardial infarction in single-beat ECG using Dual-Q TQWT and wavelet packet tensor decomposition. Comput. Meth. Prog. Biomed. 2020, 184, 105120.
- Adam, M.; Oh, S.L.; Sudarshan, V.K.; Koh, J.E.; Hagiwara, Y.; Tan, J.H.; San Tan, R.; Acharya, U.R. Automated characterization of cardiovascular diseases using relative wavelet nonlinear features extracted from ECG signals. Comput. Meth. Prog. Biomed. 2018, 161, 133–143.
- Zamani, B.; Akbari, A.; Nasersharif, B. Evolutionary combination of kernels for nonlinear feature transformation. Inf. Sci. 2014, 274, 95–107.
- Liu, F.; Zhang, W.; Gu, S. Local linear Laplacian eigenmaps: A direct extension of LLE. Patt. Recogn. Lett. 2016, 75, 30–35.
- Li, X.; Shu, L.; Hu, H. Kernel-based nonlinear dimensionality reduction for electrocardiogram recognition. Neural Comput. Appl. 2008, 18, 1013.
- Ayesha, S.; Hanif, M.K.; Talib, R. Overview and comparative study of dimensionality reduction techniques for high dimensional data. Inf. Fusion 2020, 59, 44–58.