Tunnel Boring Machines (TBMs) typically consist of a rotating cutter head that breaks up the rock or soil and a conveyor system that removes the excavated material. TBMs are preferred over traditional drill and blast techniques due to their higher efficiency, safer working conditions, minimal environmental disturbance, and reduced project costs. TBMs have become prevalent in tunnel construction due to their high efficiency and reliability. The proliferation of data obtained from site investigations and data acquisition systems provides an opportunity for the application of machine learning (ML) techniques. ML algorithms have been successfully applied in TBM tunneling because they are particularly effective in capturing complex, non-linear relationships.
- tunnel boring machine
- machine learning
- TBM performance
- surface settlement
- time series forecasting
1. Introduction
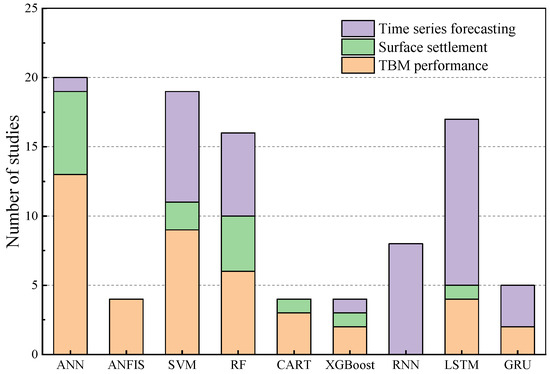
2. TBM Performance
| Literature | Data Processing a | Algorithms b | Hyperparameter Tuning c |
Targets d | Data Size and Data Set |
|---|---|---|---|---|---|
| Grima et al. [6] | PCA | MR, ANN, ANFIS | - | PR, AR | 640 tunnel project |
| Benardos and Kaliampakos [7] | - | ANN | - | AR | 11-Athens metro |
| Tiryaki [8] | PCA | MR, ANN | - | specific energy | 44-Three tunnel projects |
| Mikaeil et al. [9] | - | FL | - | Penetrability | 151-Queens water tunnel |
| Yagiz [10] | PCC | MR, ANN | - | PR | 151-Queens water tunnel |
| Javad and Narges [11] | - | ANN | - | PR | 185-Three tunnel projects |
| Mahdevari et al. [12] | - | MR, SVM | - | PR | 151-Queens water tunnel |
| Salimi et al. [13] | PCA | MR, SVM, ANFIS | - | FPI | 75-Zagros lot 1B and 2 |
| Armaghani et al. [14] | - | ANN | PSO, ICA | PR | 1286-Pahang-Selangor raw water transfer |
| Armaghani et al. [15] | - | MR, GEP | - | PR | 1286-Pahang-Selangor raw water transfer |
| Sun et al. [16] | Kriging interpolation, rate of change | RF | - | TH, TO, PR | 88-Shenzhen metro |
| Armaghani et al. [17] | - | ANN | PSO, ICA | AR | 1286-Pahang-Selangor raw water transfer |
| Koopialipoor et al. [18] | - | ANN, DNN | - | PR | 1286-Pahang-Selangor raw water transfer |
| Salimi et al. [19] | PCA | MR, CART, GP | - | FPI | 580-Seven tunnel projects |
| Zhang et al. [20] | PCC | RF | PSO | TO, TH, PR, FP | 294-Changsha metro line 4 |
| Koopialipoor et al. [21] | - | ANN | firefly algorithm | PR | 1200-Pahang-Selangor raw water transfer |
| Mokhtari and Mooney [22] | PCC, Relief | SVM | BO | PR | Northgate Link tunnel |
| Wang et al. [23] | - | ANN, LSTM, RF, SVM | - | AR | 806-Nanning metro line 1 |
| Zhang et al. [24] | - | SVM, CART, RF, bagging, Ada boosting | BO | PR | 151-Queens water tunnel |
| Zhang et al. [25] | WT, MD, GRG | LSTM, RF | PSO | TH, TO, PR, RPM, CP | 3549-Changsha metro line 4 and Zhengzhou metro line 2 |
| Zhou et al. [26] | - | ANN, GP | - | AR | 1286-Pahang-Selangor raw water transfer |
| Bai et al. [27] | PCC, Seasonal-trend decomposition | MR, SVM, DT, GBoost | - | TO, TH, FP | 450-Xi’an metro |
| Bardhan et al. [28] | - | hybrid ensemble model | - | PR | 185-Three tunnel project |
| Harandizadeh et al. [29] | - | ANFIS-PNN | ICA | PR | 209-Pahang-Selangor raw water transfer |
| Lin et al. [30] | - | MR, ANN, SVM, LSTM, GRU, EML | PR | 1000-Shenzhen railway | |
| Parsajoo et al. [31] | - | ANFIS | artificial bee colony | FPI | 150-Queens water tunnel |
| Zeng et al. [32] | - | EML | PSO | AR | 1286-Pahang-Selangor raw water transfer |
| Zhou et al. [33] | - | XGBoost | BO | AR | 1286-Pahang-Selangor raw water transfer |
| Zhou et al. [34] | - | ANN, RF, XGBoost, SVM | GWO, PSO, SCA, SSO, MVO, MFO | PR | 1286-Pahang-Selangor raw water transfer |
| Lin et al. [4] | - | LSTM | PSO | TH | 1500-Shenzhen railway |
| Lin et al. [35] | - | GRU | PSO | TO | 1500-Shenzhen railway |
| Salimi et al. [36] | - | MR, CART | - | FPI | 666-Eight tunnel projects |
| Yang et al. [37] | - | SVM | GWO, biogeography-based optimisation | PR | 503-Shenzhen metro line |
| Model Type | Dataset | Data Size | Parameters | Open Access | Limitations |
|---|---|---|---|---|---|
| Model A | 640 tunnel projects | - | Geological conditions, Operational parameters, TBM type and size |
No | hard to access |
| Model B | Queen water tunnel | 151 | Geological conditions | Yes | overfitting or lack of generalisability |
| Model C | Pahang-Selangor raw water transfer | 1286 | Geological conditions, Operational parameters |
Yes | hard to apply in practice |
3. Surface Settlement
| Literature | Data Processing | Algorithms a | Hyperparameter Tuning | Targets | Data Size and Data Set |
|---|---|---|---|---|---|
| Suwansawat and Einstein [44] | - | ANN | - | Smax | 49-Bangkok subway project |
| Boubou et al. [45] | - | ANN | - | S(X) | 432-Toulouse subway line B |
| Pourtaghi and Lotfollahi-Yaghin [46] | - | Wavelet-ANN | - | Smax | 49-Bangkok subway project |
| Dindarloo and Siami-Irdemoosa [47] | PCC | CART | - | Smax | 34-Various tunnel projects |
| Goh et al. [48] | - | MARS | - | Smax | 148-Three Singapore MRT projects |
| Chen et al. [49] | PCC | ANN, RBF, GRNN | - | Smax | 200-Changsha metro line 4 |
| Zhang et al. [20] | PCC | RF | PSO | Smax | 294-Changsha metro line 4 |
| Zhang et al. [50] | PCC | ANN, SVM, RF, EML, GRNN | PSO | Smax | 294-Changsha metro line 4 |
| Zhang et al. [25] | WT, MD, GRG | LSTM, RF | PSO | Smax | 423-Changsha metro line 4 |
| Zhang et al. [51] | PCC | XGBoost, ANN, SVM, MARS | - | Smax | 148-Three Singapore MRT projects |
| Kannangara et al. [52] | PCC, sequential feature selection, Boruta algorithm | RF | - | Smax | 264-Hangzhou metro line 2 and line 6 |
4. Time Series Forecasting
| Literature | Data Processing a | Algorithms b | Hyperparameter Tuning | Targets c | Data Size and Data Set |
|---|---|---|---|---|---|
| Guo et al. [57] | WT | Elman RNN | PSO | longitudinal settlement | Jiangji subway tunnel |
| Zhang et al. [58] | WT | ANN, SVM | - | daily settlement | 60-Wuhan metro line 2 |
| Gao et al. [59] | - | RNN, LSTM, GRU, SVM. RF, Lasso | - | TO, TH, AR, CP | 3000-Shenzhen metro |
| Zhou et al. [60] | WT | ARIMA, LSTM, CNN-LSTM | - | HDSH, HDST, VDSH, VDST, roll, pitch |
5005-Sanyang Road Tunnel |
| Gao et al. [61] | 3-sigma rule, MA, GRG | GRU | genetic algorithm | earth pressure | 1538-Luoyang metro line 2 |
| Erharter and Marcher [62] | PCC | LSTM, RF, SVM | - | TO | 200,000-Brenner base tunnel |
| Feng et al. [1] | 3-sigma rule, WT | DBN | - | FPI | 8915-Yingsong water diversion project |
| Gao et al. [63] | - | ARIMA, RNN, LSTM | - | PR | Hangzhou second water source project |
| Li et al. [64] | PCC | LSTM | - | TO, TH | 4650-Yingsong water diversion project |
| Qin et al. [65] | cosine similarity | CNN-LSTM, XGBoost, RF, SVM, LSTM, RNN, CNN | - | TO | 150,000-Singapore metro T225 project |
| Shi et al. [66] | WT, variational mode decomposition | LSTM, CNN, RNN, SVM, RF | - | TO | 60,000-Singapore metro T225 project |
| Wang et al. [56] | WT, light gradient boosting machine | LSTM | - | PR, TO | 25,543-Sutong gas transmission line |
| Xu et al. [53] | 3-sigma rule, MA, PCC | SVM, RF, CNN, LSTM, GBoost, KNN, Bayesian ridge regression | - | PR, TO, TH, RPM | 7000-Yingsong water diversion project |
| Zhang et al. [67] | - | RF | - | Smax | 386-Changsha Metro Line 4 |
| Huang et al. [68] | SelectKBest | LSTM | BO | TO | Yingsong water diversion project |
| Shan et al. [55] | MA | RNN, LSTM | - | PR | 463-Changsha metro line 4 and Zhengzhou metro line 2 |
| Shen et al. [54] | WT, Kriging interpolation | LSTM, SVM, RNN | - | HDSH, HDST, VDSH, VDST, roll, pitch | 1200-Shenzhen intercity railway |
| Zhang et al. [5] | PCA, PCC | GRU, RNN, SVM | - | HDSH, HDST, VDSH, VDST, | 22,010-Guang-Fo intercity railway |
| Literature | Category | Historical Data | Forecast Horizon | ||
|---|---|---|---|---|---|
| Step behind | Distance behind | Step ahead | Distance ahead | ||
| Gao et al. [59] | high-frequency | 5 steps | 1.25 mm a | 1 step | 0.25 mm a |
| Qin et al. [65] | 10 steps | - | 1 step | - | |
| Huang et al. [68] | 6 steps | 22.4 mm a | 1 step | 3.73 mm a | |
| Erharter and Marcher [62] | 50 steps | 2.75 m | 1 or 100 steps | 0.055 or 5.5 m | |
| Shi et al. [66] | 10 steps | - | 1–5 steps | - | |
| Gao et al. [61] | low-frequency | 5 steps | 7.5 m | 1 step | 1.5 m |
| Feng et al. [1] | 7 steps | 7 m | 1 step | 1 m | |
| Shan et al. [55] | 5 steps | 7.5 m | 1–5 steps | 1.5–7.5 m |
This entry is adapted from the peer-reviewed paper 10.3390/eng4020087
References
- Feng, S.; Chen, Z.; Luo, H.; Wang, S.; Zhao, Y.; Liu, L.; Ling, D.; Jing, L. Tunnel boring machines (TBM) performance prediction: A case study using big data and deep learning. Tunn. Undergr. Space Technol. 2021, 110, 103636.
- Chen, Z.; Zhang, Y.; Li, J.; Li, X.; Jing, L. Diagnosing tunnel collapse sections based on TBM tunneling big data and deep learning: A case study on the Yinsong Project, China. Tunn. Undergr. Space Technol. 2021, 108, 103700.
- Liu, B.; Wang, R.; Zhao, G.; Guo, X.; Wang, Y.; Li, J.; Wang, S. Prediction of rock mass parameters in the TBM tunnel based on BP neural network integrated simulated annealing algorithm. Tunn. Undergr. Space Technol. 2020, 95, 103103.
- Lin, S.; Zhang, N.; Zhou, A.; Shen, S. Time-series prediction of shield movement performance during tunneling based on hybrid model. Tunn. Undergr. Space Technol. 2022, 119, 104245.
- Zhang, N.; Zhang, N.; Zheng, Q.; Xu, Y.-S. Real-time prediction of shield moving trajectory during tunnelling using GRU deep neural network. Acta Geotech. 2022, 17, 1167–1182.
- Grima, M.A.; Bruines, P.; Verhoef, P. Modeling tunnel boring machine performance by neuro-fuzzy methods. Tunn. Undergr. Space Technol. 2000, 15, 259–269.
- Benardos, A.; Kaliampakos, D. Modelling TBM performance with artificial neural networks. Tunn. Undergr. Space Technol. 2004, 19, 597–605.
- Tiryaki, B. Application of artificial neural networks for predicting the cuttability of rocks by drag tools. Tunn. Undergr. Space Technol. 2008, 23, 273–280.
- Mikaeil, R.; Naghadehi, M.Z.; Sereshki, F. Multifactorial fuzzy approach to the penetrability classification of TBM in hard rock conditions. Tunn. Undergr. Space Technol. 2009, 24, 500–505.
- Yagiz, S. Assessment of brittleness using rock strength and density with punch penetration test. Tunn. Undergr. Space Technol. 2009, 24, 66–74.
- Javad, G.; Narges, T. Application of artificial neural networks to the prediction of tunnel boring machine penetration rate. Min. Sci. Technol. 2010, 20, 727–733.
- Mahdevari, S.; Shahriar, K.; Yagiz, S.; Shirazi, M.A. A support vector regression model for predicting tunnel boring machine penetration rates. Int. J. Rock Mech. Min. Sci. 2014, 72, 214–229.
- Salimi, A.; Rostami, J.; Moormann, C.; Delisio, A. Application of non-linear regression analysis and artificial intelligence algorithms for performance prediction of hard rock TBMs. Tunn. Undergr. Space Technol. 2016, 58, 236–246.
- Armaghani, D.J.; Mohamad, E.T.; Narayanasamy, M.S.; Narita, N.; Yagiz, S. Development of hybrid intelligent models for predicting TBM penetration rate in hard rock condition. Tunn. Undergr. Space Technol. 2017, 63, 29–43.
- Armaghani, D.J.; Faradonbeh, R.S.; Momeni, E.; Fahimifar, A.; Tahir, M. Performance prediction of tunnel boring machine through developing a gene expression programming equation. Eng. Comput. 2018, 34, 129–141.
- Sun, W.; Shi, M.; Zhang, C.; Zhao, J.; Song, X. Dynamic load prediction of tunnel boring machine (TBM) based on heterogeneous in-situ data. Autom. Constr. 2018, 92, 23–34.
- Armaghani, D.J.; Koopialipoor, M.; Marto, A.; Yagiz, S. Application of several optimization techniques for estimating TBM advance rate in granitic rocks. J. Rock Mech. Geotech. Eng. 2019, 11, 779–789.
- Koopialipoor, M.; Tootoonchi, H.; Jahed Armaghani, D.; Tonnizam Mohamad, E.; Hedayat, A. Application of deep neural networks in predicting the penetration rate of tunnel boring machines. Bull. Eng. Geol. Environ. 2019, 78, 6347–6360.
- Salimi, A.; Rostami, J.; Moormann, C. Application of rock mass classification systems for performance estimation of rock TBMs using regression tree and artificial intelligence algorithms. Tunn. Undergr. Space Technol. 2019, 92, 103046.
- Zhang, P.; Chen, R.; Wu, H. Real-time analysis and regulation of EPB shield steering using Random Forest. Autom. Constr. 2019, 106, 102860.
- Koopialipoor, M.; Fahimifar, A.; Ghaleini, E.N.; Momenzadeh, M.; Armaghani, D.J. Development of a new hybrid ANN for solving a geotechnical problem related to tunnel boring machine performance. Eng. Comput. 2020, 36, 345–357.
- Mokhtari, S.; Mooney, M.A. Predicting EPBM advance rate performance using support vector regression modeling. Tunn. Undergr. Space Technol. 2020, 104, 103520.
- Wang, Q.; Xie, X.; Shahrour, I. Deep learning model for shield tunneling advance rate prediction in mixed ground condition considering past operations. IEEE Access 2020, 8, 215310–215326.
- Zhang, Q.; Hu, W.; Liu, Z.; Tan, J. TBM performance prediction with Bayesian optimization and automated machine learning. Tunn. Undergr. Space Technol. 2020, 103, 103493.
- Zhang, P.; Wu, H.; Chen, R.; Dai, T.; Meng, F.; Wang, H. A critical evaluation of machine learning and deep learning in shield-ground interaction prediction. Tunn. Undergr. Space Technol. 2020, 106, 103593.
- Zhou, J.; Yazdani Bejarbaneh, B.; Jahed Armaghani, D.; Tahir, M. Forecasting of TBM advance rate in hard rock condition based on artificial neural network and genetic programming techniques. Bull. Eng. Geol. Environ. 2020, 79, 2069–2084.
- Bai, X.-D.; Cheng, W.-C.; Li, G. A comparative study of different machine learning algorithms in predicting EPB shield behaviour: A case study at the Xi’an metro, China. Acta Geotech. 2021, 16, 4061–4080.
- Bardhan, A.; Kardani, N.; GuhaRay, A.; Burman, A.; Samui, P.; Zhang, Y. Hybrid ensemble soft computing approach for predicting penetration rate of tunnel boring machine in a rock environment. J. Rock Mech. Geotech. Eng. 2021, 13, 1398–1412.
- Harandizadeh, H.; Armaghani, D.J.; Asteris, P.G.; Gandomi, A.H. TBM performance prediction developing a hybrid ANFIS-PNN predictive model optimized by imperialism competitive algorithm. Neural Comput. Appl. 2021, 33, 16149–16179.
- Lin, S.; Shen, S.; Zhang, N.; Zhou, A. Modelling the performance of EPB shield tunnelling using machine and deep learning algorithms. Geosci. Front. 2021, 12, 101177.
- Parsajoo, M.; Mohammed, A.S.; Yagiz, S.; Armaghani, D.J.; Khandelwal, M. An evolutionary adaptive neuro-fuzzy inference system for estimating field penetration index of tunnel boring machine in rock mass. J. Rock Mech. Geotech. Eng. 2021, 13, 1290–1299.
- Zeng, J.; Roy, B.; Kumar, D.; Mohammed, A.S.; Armaghani, D.J.; Zhou, J.; Mohamad, E.T. Proposing several hybrid PSO-extreme learning machine techniques to predict TBM performance. Eng. Comput. 2021, 38, 3811–3827.
- Zhou, J.; Qiu, Y.; Zhu, S.; Armaghani, D.J.; Khandelwal, M.; Mohamad, E.T. Estimation of the TBM advance rate under hard rock conditions using XGBoost and Bayesian optimization. Undergr. Space 2021, 6, 506–515.
- Zhou, J.; Qiu, Y.; Armaghani, D.J.; Zhang, W.; Li, C.; Zhu, S.; Tarinejad, R. Predicting TBM penetration rate in hard rock condition: A comparative study among six XGB-based metaheuristic techniques. Geosci. Front. 2021, 12, 101091.
- Lin, S.-S.; Shen, S.-L.; Zhou, A. Real-time analysis and prediction of shield cutterhead torque using optimized gated recurrent unit neural network. J. Rock Mech. Geotech. Eng. 2022, 14, 1232–1240.
- Salimi, A.; Rostami, J.; Moormann, C.; Hassanpour, J. Introducing Tree-Based-Regression Models for Prediction of Hard Rock TBM Performance with Consideration of Rock Type. Rock Mech. Rock Eng. 2022, 55, 4869–4891.
- Yang, H.; Wang, Z.; Song, K. A new hybrid grey wolf optimizer-feature weighted-multiple kernel-support vector regression technique to predict TBM performance. Eng. Comput. 2022, 38, 2469–2485.
- Yang, J.; Yagiz, S.; Liu, Y.-J.; Laouafa, F. Comprehensive evaluation of machine learning algorithms applied to TBM performance prediction. Undergr. Space 2022, 7, 37–49.
- Yagiz, S.; Karahan, H. Application of various optimization techniques and comparison of their performances for predicting TBM penetration rate in rock mass. Int. J. Rock Mech. Min. Sci. 2015, 80, 308–315.
- Zhang, W.; Li, H.; Li, Y.; Liu, H.; Chen, Y.; Ding, X. Application of deep learning algorithms in geotechnical engineering: A short critical review. Artif. Intell. Rev. 2021, 54, 5633–5673.
- Ahangari, K.; Moeinossadat, S.R.; Behnia, D. Estimation of tunnelling-induced settlement by modern intelligent methods. Soils Found. 2015, 55, 737–748.
- Neaupane, K.M.; Adhikari, N. Prediction of tunneling-induced ground movement with the multi-layer perceptron. Tunn. Undergr. Space Technol. 2006, 21, 151–159.
- Santos, O.J., Jr.; Celestino, T.B. Artificial neural networks analysis of Sao Paulo subway tunnel settlement data. Tunn. Undergr. Space Technol. 2008, 23, 481–491.
- Suwansawat, S.; Einstein, H.H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling. Tunn. Undergr. Space Technol. 2006, 21, 133–150.
- Boubou, R.; Emeriault, F.; Kastner, R. Artificial neural network application for the prediction of ground surface movements induced by shield tunnelling. Can. Geotech. J. 2010, 47, 1214–1233.
- Pourtaghi, A.; Lotfollahi-Yaghin, M. Wavenet ability assessment in comparison to ANN for predicting the maximum surface settlement caused by tunneling. Tunn. Undergr. Space Technol. 2012, 28, 257–271.
- Dindarloo, S.R.; Siami-Irdemoosa, E. Maximum surface settlement based classification of shallow tunnels in soft ground. Tunn. Undergr. Space Technol. 2015, 49, 320–327.
- Goh, A.T.C.; Zhang, W.; Zhang, Y.; Xiao, Y.; Xiang, Y. Determination of earth pressure balance tunnel-related maximum surface settlement: A multivariate adaptive regression splines approach. Bull. Eng. Geol. Environ. 2018, 77, 489–500.
- Chen, R.-P.; Zhang, P.; Kang, X.; Zhong, Z.-Q.; Liu, Y.; Wu, H.-N. Prediction of maximum surface settlement caused by earth pressure balance (EPB) shield tunneling with ANN methods. Soils Found. 2019, 59, 284–295.
- Zhang, P.; Wu, H.-N.; Chen, R.-P.; Chan, T.H. Hybrid meta-heuristic and machine learning algorithms for tunneling-induced settlement prediction: A comparative study. Tunn. Undergr. Space Technol. 2020, 99, 103383.
- Zhang, W.; Li, H.; Wu, C.; Li, Y.; Liu, Z.; Liu, H. Soft computing approach for prediction of surface settlement induced by earth pressure balance shield tunneling. Undergr. Space 2021, 6, 353–363.
- Kannangara, K.P.M.; Zhou, W.; Ding, Z.; Hong, Z. Investigation of feature contribution to shield tunneling-induced settlement using Shapley additive explanations method. J. Rock Mech. Geotech. Eng. 2022, 14, 1052–1063.
- Xu, C.; Liu, X.; Wang, E.; Wang, S. Prediction of tunnel boring machine operating parameters using various machine learning algorithms. Tunn. Undergr. Space Technol. 2021, 109, 103699.
- Shen, S.-L.; Elbaz, K.; Shaban, W.M.; Zhou, A. Real-time prediction of shield moving trajectory during tunnelling. Acta Geotech. 2022, 17, 1533–1549.
- Shan, F.; He, X.; Armaghani, D.J.; Zhang, P.; Sheng, D. Success and challenges in predicting TBM penetration rate using recurrent neural networks. Tunn. Undergr. Space Technol. 2022, 130, 104728.
- Wang, R.; Li, D.; Chen, E.J.; Liu, Y. Dynamic prediction of mechanized shield tunneling performance. Autom. Constr. 2021, 132, 103958.
- Guo, J.; Ding, L.; Luo, H.; Zhou, C.; Ma, L. Wavelet prediction method for ground deformation induced by tunneling. Tunn. Undergr. Space Technol. 2014, 41, 137–151.
- Zhang, L.; Wu, X.; Ji, W.; AbouRizk, S.M. Intelligent approach to estimation of tunnel-induced ground settlement using wavelet packet and support vector machines. J. Comput. Civ. Eng. 2017, 31, 04016053.
- Gao, X.; Shi, M.; Song, X.; Zhang, C.; Zhang, H. Recurrent neural networks for real-time prediction of TBM operating parameters. Autom. Constr. 2019, 98, 225–235.
- Zhou, C.; Xu, H.; Ding, L.; Wei, L.; Zhou, Y. Dynamic prediction for attitude and position in shield tunneling: A deep learning method. Autom. Constr. 2019, 105, 102840.
- Gao, M.-Y.; Zhang, N.; Shen, S.-L.; Zhou, A. Real-time dynamic earth-pressure regulation model for shield tunneling by integrating GRU deep learning method with GA optimization. IEEE Access 2020, 8, 64310–64323.
- Erharter, G.H.; Marcher, T. On the pointlessness of machine learning based time delayed prediction of TBM operational data. Autom. Constr. 2021, 121, 103443.
- Gao, B.; Wang, R.; Lin, C.; Guo, X.; Liu, B.; Zhang, W. TBM penetration rate prediction based on the long short-term memory neural network. Undergr. Space 2021, 6, 718–731.
- Li, J.; Li, P.; Guo, D.; Li, X.; Chen, Z. Advanced prediction of tunnel boring machine performance based on big data. Geosci. Front. 2021, 12, 331–338.
- Qin, C.; Shi, G.; Tao, J.; Yu, H.; Jin, Y.; Lei, J.; Liu, C. Precise cutterhead torque prediction for shield tunneling machines using a novel hybrid deep neural network. Mech. Syst. Signal Process. 2021, 151, 107386.
- Shi, G.; Qin, C.; Tao, J.; Liu, C. A VMD-EWT-LSTM-based multi-step prediction approach for shield tunneling machine cutterhead torque. Knowl.-Based Syst. 2021, 228, 107213.
- Zhang, P.; Chen, R.; Dai, T.; Wang, Z.; Wu, K. An AIoT-based system for real-time monitoring of tunnel construction. Tunn. Undergr. Space Technol. 2021, 109, 103766.
- Huang, X.; Zhang, Q.; Liu, Q.; Liu, X.; Liu, B.; Wang, J.; Yin, X. A real-time prediction method for tunnel boring machine cutter-head torque using bidirectional long short-term memory networks optimized by multi-algorithm. J. Rock Mech. Geotech. Eng. 2022, 14, 798–812.
- Qin, C.; Shi, G.; Tao, J.; Yu, H.; Jin, Y.; Xiao, D.; Zhang, Z.; Liu, C. An adaptive hierarchical decomposition-based method for multi-step cutterhead torque forecast of shield machine. Mech. Syst. Signal Process. 2022, 175, 109148.
- Shan, F.; He, X.; Armaghani, D.J.; Zhang, P.; Sheng, D. Response to Discussion on “Success and challenges in predicting TBM penetration rate using recurrent neural networks” by Georg H. Erharter, Thomas Marcher. Tunn. Undergr. Space Technol. 2023, 105064.
