You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Deepfake Identification and Traceability: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Yi Sun
,
Jun Zheng
,
Lingjuan Lyn
,
Hanyu Zhao
,
Jiaxing Li
,
Yunteng Tan
,
Xinyu Liu
,
Yuanzhang Li

Deepfakes are becoming increasingly ubiquitous, particularly in facial manipulation. Numerous researchers and companies have released multiple datasets of face deepfakes labeled to indicate different methods of forgery. However, naming these labels is often arbitrary and inconsistent, leading to the fact that most researchers now choose to use only one of the datasets for research work. However, researchers must use these datasets in practical applications and conduct traceability research. In this study, we employ some models to extract forgery features from various deepfake datasets and utilize the K-means clustering method to identify datasets with similar feature values. We analyze the feature values using the Calinski Harabasz Index method. Our findings reveal that datasets with the same or similar labels in different deepfake datasets exhibit different forgery features. We proposed the KCE system to solve this problem, which combines multiple deepfake datasets according to feature similarity. We analyzed four groups of test datasets and found that the model trained based on KCE combined data faced unknown data types, and Calinski Harabasz scored 42.3% higher than combined by forged names. Furthermore, it is 2.5% higher than the model using all data, although the latter has more training data. It shows that this method improves the generalization ability of the model. This paper introduces a fresh perspective for effectively evaluating and utilizing diverse deepfake datasets and conducting deepfake traceability research.

  • deepfake
  • datasets
  • correlation
  • traceability
  • clustering
  • Calinski Harabasz

1. Introduction

Facial recognition has become increasingly prevalent in recent years, with many applications utilizing it as the primary method for identity recognition. However, with the rapid development of deep learning-driven facial forgery technologies in recent years, such as deepfakes [1], there has been a rise in fraudulent practices within media and financial fields, which has sparked widespread social concern [2][3][4]. Consequently, there is a crucial need for the traceability of forged data.
Deepfake tracking methods can be broadly classified into traditional [5][6][7] and deep learning-based methods [8][9]. Traditional methods rely on techniques, such as image forensics and metadata analysis to detect signs of manipulation in a deepfake. These methods are based on analyzing the visual properties of an image or video, and they can include analyzing the distribution of colors, identifying inconsistencies in lighting and shadows, or detecting distortions in the image caused by manipulation. These traditional methods require extensive domain knowledge and specialized software to execute. On the other hand, deep learning-based methods rely on machine learning algorithms’ power to detect deepfakes. These methods train deep neural networks on large datasets of real and fake images or videos, and they can detect deepfakes by analyzing the patterns in the data. Deep learning-based methods are highly effective at detecting deepfakes, but they require large amounts of training data and computing resources to execute. This paper mainly conducts related research based on the latter method.
Tracing the source of deep forgery relies on identifying the forgery algorithms used. However, the category labels in deepfake datasets fundamentally differ from those in the general computer vision field. In typical computer vision datasets, such as the CIFAR [10], ImageNet [11], and MNIST [12], the category labels are objective and have real-world meaning. For instance, the labels for salamander and setosa are assigned by biologists based on the biological characteristics of these species, or humans can accurately recognize facial expressions such as anger or happiness, as shown in Figure 1. These labels remain unchanged despite variations in camera equipment, lighting conditions, and post-processing of images. However, humans cannot classify deepfake pictures visually, and the images can only be named based on their forgery method. The names given to the forgery methods by different producers are highly subjective and arbitrary. Many “wild datasets” do not provide forgery method labels. Furthermore, subsequent operations such as image compression and format conversion [13] may significantly alter the forgery characteristics of the images.
电子 12 02353 g001 550
Figure 1. The first row shows the common CV dataset, the second row shows the human facial expression dataset, and the third row shows the deepfake dataset.
Improving facial forgery recognition and tracking technology relies on collecting and utilizing as many facial forgery datasets as possible. These datasets include ForgeryNet [14], DeepfakeTIMIT [15], FakeAVCeleb [16], DeeperForensics-1.0 [17], and others. Additionally, numerous “wild datasets” are gathered from the Internet. However, these datasets are published by different institutions, use varying forgery methods, and have different naming conventions. In some cases, the exact generation algorithm is not provided. This situation leads some researchers to use only one dataset in their experiments. Dealing with those with similar or identical names can create challenges for users when multiple datasets are employed.
Measuring the relevance of each deepfake dataset is crucial. To address this problem, we use the Xception model [18] as a forgery feature extractor, commonly used in deepfake recognition. We train both multi-classification and binary classification models that map various deepfake images into the feature space illustrated in Figure 2.
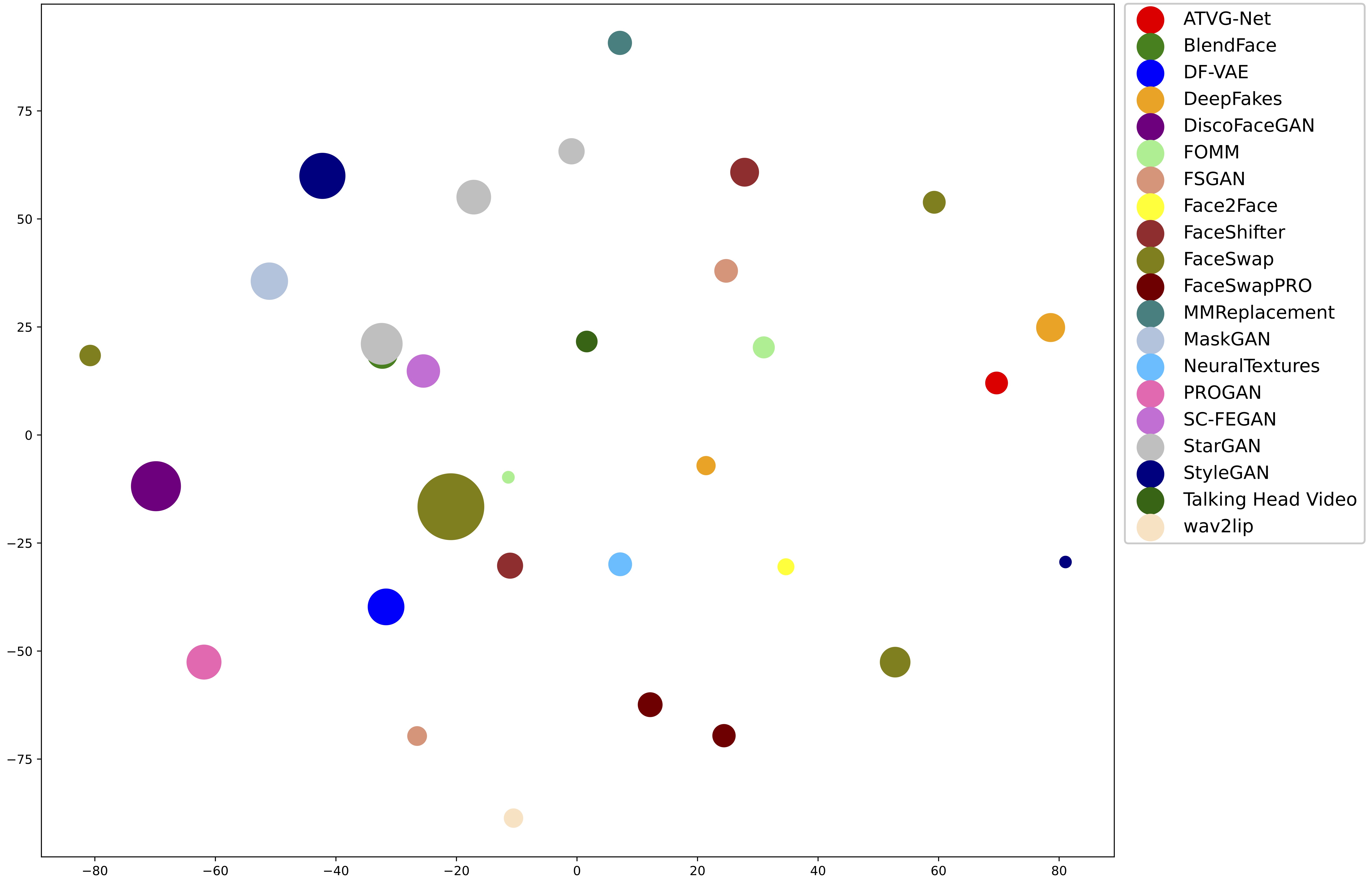
The circle’s center represents the center position of this category of the dataset, and the area of the circle represents the rank of the Covariance Matrix of these datasets. Distances between the fake datasets represent the similarity of these fake features.
Figure 2. The circle’s center represents the center position of this category of the dataset, and the area of the circle represents the rank of the Covariance Matrix of these datasets. Distances between the fake datasets represent the similarity of these fake features.
After mapping the deepfake datasets to feature space, we use PCA for dimensionality reduction and the K-means method for clustering. We use these cluster datasets to retrain the Xception model. We also combine these deepfake datasets based on forgery method labels and use them to train another Xception model as a control group. We perform a series of experiments on the test data using these models and use the Calinski Harabasz Index [19] as a measure to judge the performance of the models. To improve the credibility of the experimental results, we also repeat some experiments on The Frequency in Face Forgery Network (F3-Net) [9] and Residual Neural network (ResNet) [20]. Our main contributions are summarized as follows:
  • We point out that the forgery category labels in the deepfake dataset lack objectivity. Our experiments prove that some forgery category labels of the same name differ significantly across different datasets.
  • We establish the KCE-System. It is a deepfake dataset similarity evaluation index system that provides a measure of the similarity between different datasets and lays the foundation for subsequent researchers to use these datasets comprehensively.
  • Our experiments confirm that when the forgery method of the deepfake dataset is unknown, the model can achieve better generalization performance by training on datasets that are merged based on closer feature distances.

2. Related Works

2.1 Deepfake Datasets

Numerous deepfake datasets have been created by researchers and institutions, including FaceForensics++ [21], Celeb-DF [22], DeepFakeMnist+ [15], DeepfakeTIMIT [1], FakeAVCeleb [16], DeeperForensics-1.0 [17], ForgeryNet [14], and Patch-wise Face Image Forensics [23]. These datasets cover various forgery methods, have significant data scales, and are widely used. Please refer to Table 1 for more details.
Table 1. The standard deepfake datasets. The symbol * represents the number of pictures.
Dataset Real Fake Forgery Method
CelebDFv1 [22] 409 795 FaceswapPro
CelebDFv2 [22] 590 5639 FaceswapPro
DeeperForensics1.0 [17] 50,000 10,000 DeepFake Variational Auto-Encoder (DF-VAE) [24]
FakeAVCeleb [16] 178 11,833 Faceswap [25], Faceswap GAN (FSGAN) [26], Wav2Lip [27]
DeepFakeMnist+ [15] 10,000 10,000 First Order Motion Model for Image Animation (FOMM) [28]
DeepfakeTIMIT [1] 320 640 faceswap-GAN [29]
FaceForensics++ [21] 1000 5000 Faceswap [30], Deepfakes [31], Face2Face [32], FaceShifter [33], NeuralTextures [34]
DeepFakeDetection [35] 363 3068 Faceswap
ForgeryNet [14] 99,630 121,617 ATVG-Net [36], BlendFace, DeepFakes, DeepFakes-StarGAN-Stack, DiscoFaceGAN [37], FaceShifter [33], FOMM [28], FS-GAN [26], MaskGAN [38], MMReplacement, SC-FEGAN [39], StarGAN-BlendFace-Stack, StarGAN2 [40], StyleGAN2 [41], Talking Head Video [42]
Patch-wise Face Image Forensics [23] * 25,000 * 25,000 PROGAN [43], StyleGAN2 [41]

2.2 Deepfake Identification and Traceability

2.2.1 Methods Based on Spectral Features

Many scholars consider upsampling to be a necessary step in generating most face forgeries. Cumulative upsampling can cause apparent changes in the frequency domain, and minor forgery defects and compression errors can be well described in this domain. Using this information can identify fake videos. Spectrum-based methods have certain advantages in generalization because they provide another perspective. Most existing image and video compression methods are also related to the frequency domain, making the method based on this domain particularly robust.
Chen et al. [44] proposed a forgery detection algorithm that combines spatial and frequency domain features using an attention mechanism. The method uses a convolutional neural network and an attention mechanism to extract spatial domain features. After the Fourier transform, the frequency domain features are extracted, and finally, these features are fused for classification. Qian et al. [9] proposed a network structure called F3-Net (Frequency in Face Forgery Network) and designed a two-stream collaborative learning framework to learn the frequency domain adaptive image decomposition branch and image detail frequency statistics branch. The method has a significant lead over other methods on low-quality video. Liu et al. [45] proposed a method based on Spatial Phase Shallow Learning (SPSL). The method combines spatial images and phase spectra to capture upsampled features of facial forgery. For forgery detection tasks, local texture information is more critical than high-level semantic information. By making the network shallower, the network is more focused on local regions. Li et al. [46] proposed a learning framework based on frequency-aware discriminative features. They designed a single-center loss function (SCL), which only compresses the intra-class variation of real faces while enhancing the inter-class variation in the embedding space. In this way, the network can learn more discriminative features with less optimization difficulty.

2.2.2 Methods Based on Generative Adversarial Network Inherent Traces

Scholars suggest that fake faces generated by generative adversarial networks have distinct traces and texture information compared to real-world photographs.
Guarnera et al. [47] proposed a detection method based on forgery traces, which uses an Expectation Maximization algorithm to extract local features that model the convolutional generation process. Liu et al. [48] developed GramNet, an architecture that uses global image texture representation for robust forgery detection, particularly against image disturbances such as downsampling, JPEG compression, blur, and noise. Yang et al. [49] argue that existing GAN-based forgery detection methods are limited in their ability to generalize to new training models with different random seeds, datasets, and loss functions. They propose DNA-Det, which observes that GAN architecture leaves globally consistent fingerprints, and model weights leave varying traces in different regions.

2.3 Troubles with Current Deepfake Traceability

Methods based on frequency domain and model fingerprints provide traceability for different forgery methods. Although researchers claim high accuracy rates in identifying and tracing related forgery methods, they typically only use a specific dataset for research. This approach reduces the comprehensiveness of traceability and the model’s generalization ability. Therefore, researchers need to consider the similarity and correlation between samples in each dataset to make full use of these datasets.
However, this presents a significant challenge. Unlike typical computer vision datasets, deepfake datasets’ labels are based on technical methods and forgery patterns rather than human concepts, making it impossible for humans to identify and evaluate them. The more severe problem is that the labels of forgery methods used in various deepfake datasets are entirely arbitrary. Some labels are based on implementation technology, while others are based on forgery modes. For example, many datasets have the label “DeepFakes.” The irregularity and ambiguity of these labeling methods make it difficult to fully utilize the forged data of various deepfake datasets. Some deepfake datasets do not indicate specific forgery methods, such as “wild datasets.”

3. Research Methods

3.1. K-Means and Calinski Harabasz Evaluation System

We trained an Xception model as a feature extractor using various deepfake datasets and real datasets as training sets. When examining different deepfake datasets in feature space, we observe that specific forgery methods are clustered together. In contrast, some forgery methods with similar names are separated, as shown in Figure 2. For example, one of the FOMM forgery methods is very close to the FaceSwap method but far from the other FOMM forgery methods. It shows that the forgery methods with the same name have a significant feature gap in different datasets, and different forgery methods will have relatively similar features. The same trend can be seen in the Cosine Similarity results in Figure 3. To evaluate the similarity between different forgery methods across various datasets. We assume that incorporating datasets that use the same forgery methods will beneficially enhance the model’s performance. Conversely, merging different datasets or dividing the similar dataset into separate subsets may adversely affect the model’s performance. We developed the K-means and Calinski Harabasz Evaluation System based on the above assumptions. For the sake of simplicity, we refer to it as the KCE-System for short.

Figure 3. Similarity matrices for different forgery methods in each deepfake dataset.

Figure 3. Similarity matrices for different forgery methods in each deepfake dataset.

The KCE-System incorporates unsupervised learning. The system divided the deepfake datasets into training sets and evaluation sets. Then it trains a deepfake recognition model using training sets, and extracting high-dimensional vectors from the middle layer of the model. After dimensionality reduction, the system used the K-means clustering method to merge various deepfake datasets. Using these datasets, the system then trains the new Xception, F3-net, and ResNet models. The trained models are then used to extract 2048-dimensional or 512-dimensional values from the evaluation set as feature values. Finally, the system uses the Calinski Harabasz Index method on the feature values after dimensionality reduction to evaluate The model’s performance, as shown in Figure 4. Next, we will introduce several main parts of the system in detail.

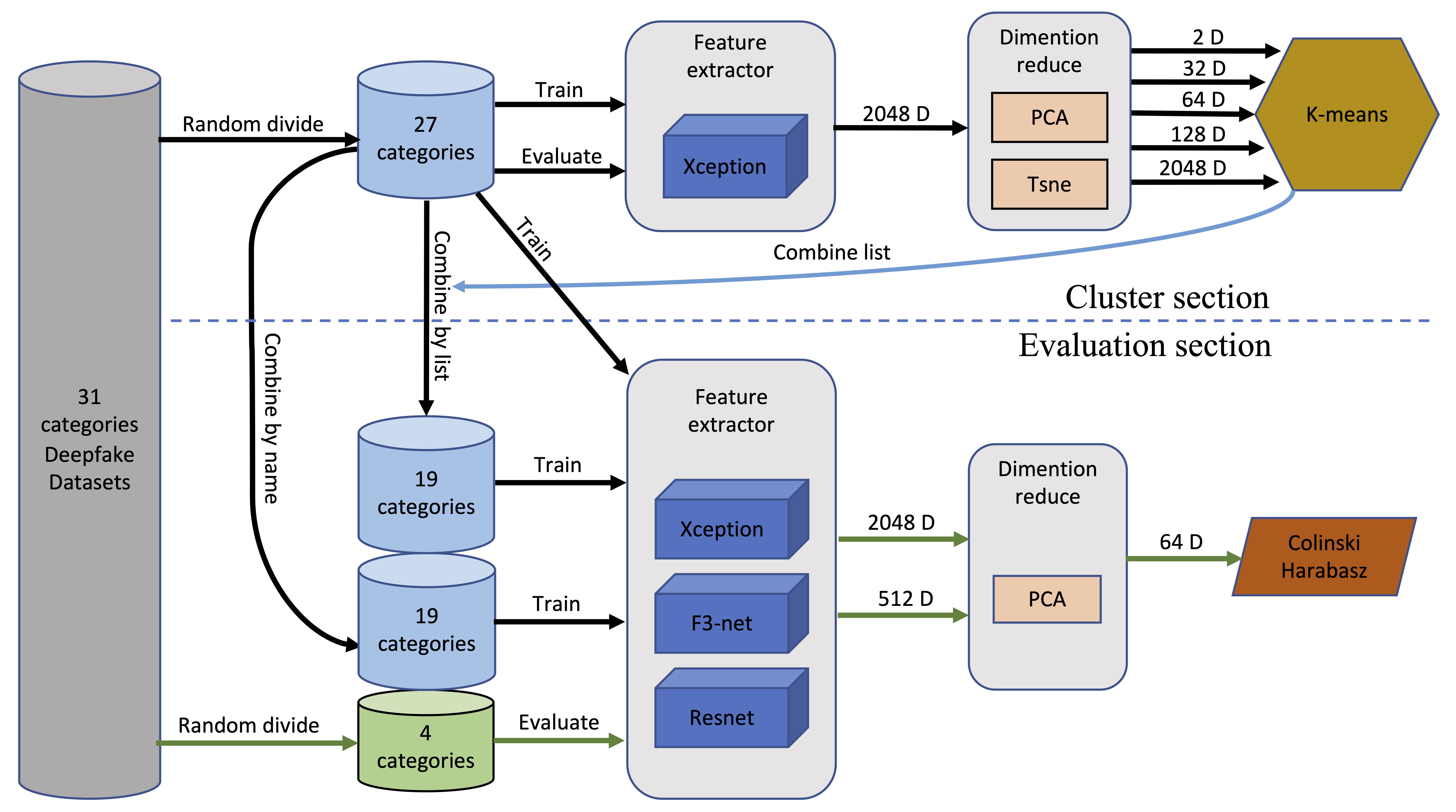
Figure 4. Overview of the KCE-System. The proposed architecture consists of two parts: the cluster section and the evaluation section.

3.2. Feature Extractor

Theoretically, when a model reaches a high classification accuracy for various categories of deep fake data, the model can extract the corresponding deepfake feature. We use the trained deepfake recognition model as a feature extractor, as the accuracy of these models in deepfake multi-classification tasks can reach more than 90%. For a comprehensive evaluation, we provide several representative models with different sizes.

The Xception [18] is a traditional CNN model based on separable convolutions with residual connections. The model has shown high accuracy when detecting deepfake videos. In terms of the training process of the feature extractor, the forgery method indicated in each dataset is used as a pseudo-labelling for multi-class training on the Xception. The training accuracy rate reaches 94%, and the model converges after three training rounds. We use the trained model extract feature on the data of 27 categories of deepfake datasets. We take out its 2048-dimensional data as the sample’s feature from the global pooling layer of Xception. Considering the trade-off between performance and efficiency, we select Xception as the baseline model.

The ResNet [20] is an improvement over the traditional deep neural network architecture that solves the problem of vanishing gradients and allows the training of much deeper networks. One of the main advantages of ResNet is its ability to handle deeper architectures, which leads to better accuracy in image classification tasks. Another notable model in facial forgery detection is the F3-Net, as proposed in [9]. This model leverages frequency domain analysis and comprises two branches, one focused on learning subtle forgery patterns via Frequency-aware Image Decomposition (FAD) and the other aimed at extracting high-level semantics from Local Frequency Statistics (LFS). Extensive experiments have demonstrated the effectiveness of the F3-Net in identifying low-quality forgery videos. Given the widespread applicability of the ResNet model in various computer vision fields and the unique position of the F3-Net in the domain of deepfake detection, we also select these two models as evaluation models and test them on half of the test group. To avoid the interference of the model itself on the experimental results to the greatest extent.

3.3. Dimensionality Reduction and Clustering

In this field, clustering algorithms, such as K-means [50], Gaussian Mixture, and DBSCAN [51] are commonly used. However, the DBSCAN algorithm is ineffective in controlling the number of clusters formed. In our system, we need to control the number of clusters formed for easy comparison with the data merged by name. The Gaussian Mixture algorithm is mainly designed for non-spherical clusters, while we focus more on the distance between categories in feature space, which emphasizes spherical clustering. Therefore, we chose to use the K-means clustering algorithm in our system.

The K-means algorithm uses Euclidean distance for clustering, but it can fail in high dimensions, so a dimension reduction method must be used. PCA [52] and t-SNE [53] are two methods we utilized for comparison. PCA is stable but retains less information when reduced to two or three dimensions. When reducing dimensions to 64 using PCA, the interpretable variance contribution rate can be preserved at 95.2%. From Figure 5, we can see that it effectively preserves most of the information needed for clustering. The t-SNE supports low-dimensional reduction for visual analysis but has poor stability.

We utilize five different dimensionality reduction parameters to determine the most appropriate clustering dimension. We apply the t-SNE algorithm to reduce the high-dimensional feature data to 2 dimensions and use the PCA algorithm to reduce the dimensionality to 32,64, and 128 dimensions. We also keep the 2048 dimensional original features without applying any dimensionality reduction algorithm. We then performed K-means clustering on each of these dimensions individually.

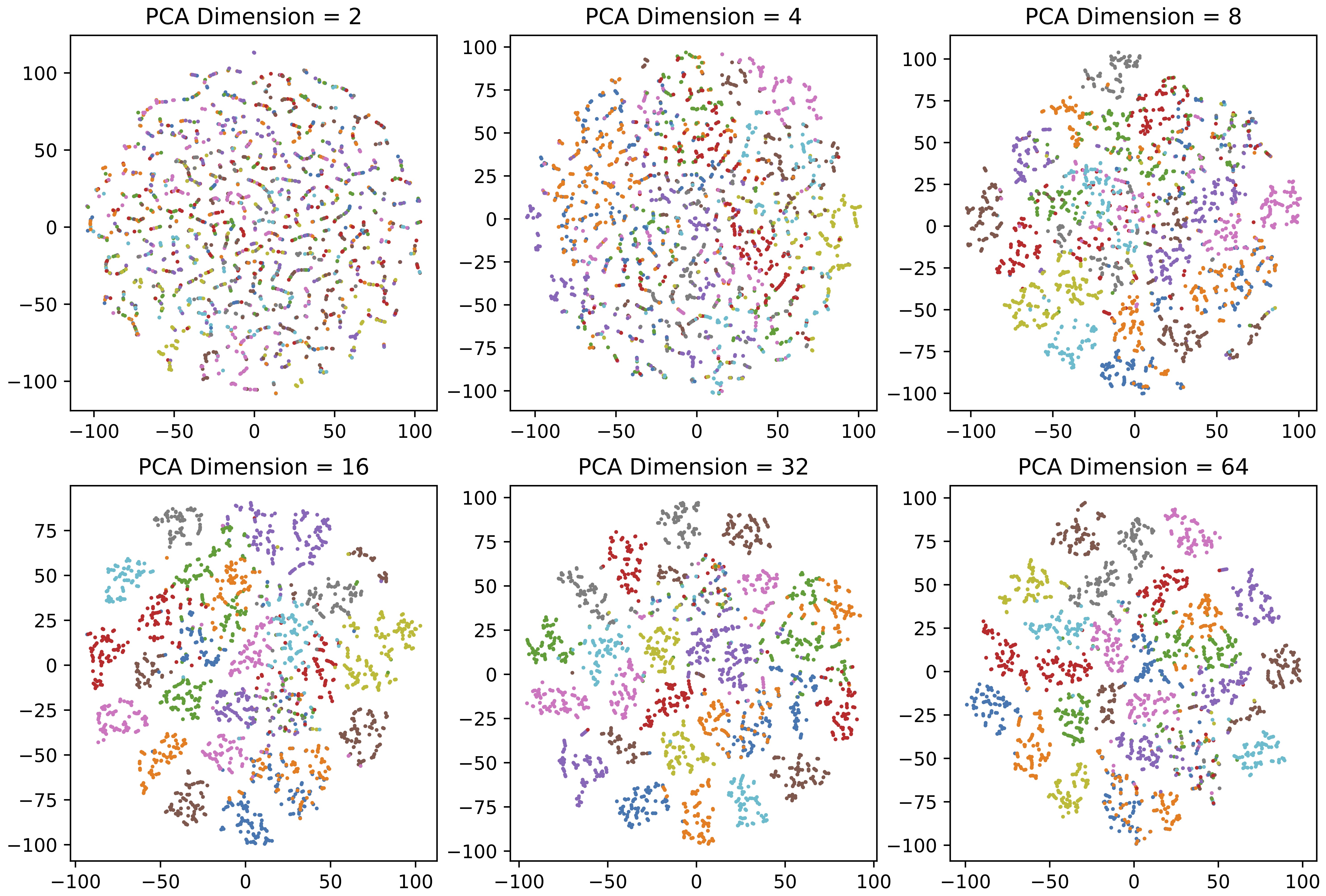
Figure 5. Illustration of dimensionality reduction using PCA. After using PCA to reduce the dimension, use the t-SNE method to reduce the dimension to two dimensions for display (Different colors indicate different forgery methods).

3.4. Selection of Evaluation Algorithms

We select four categories of deepfake datasets not involved in the training and clustering process as evaluation sets. We extract Xception, ResNet, and F3-net models’ global pooling layer output and use the PCA algorithm reduces the data to 128 dimensions. An example of the results in Figure 6, demonstrating a clear distinction between the four unknown deepfake categories. This figure indicates that our model has indeed learned the relevant characteristics for identifying deepfakes.

 

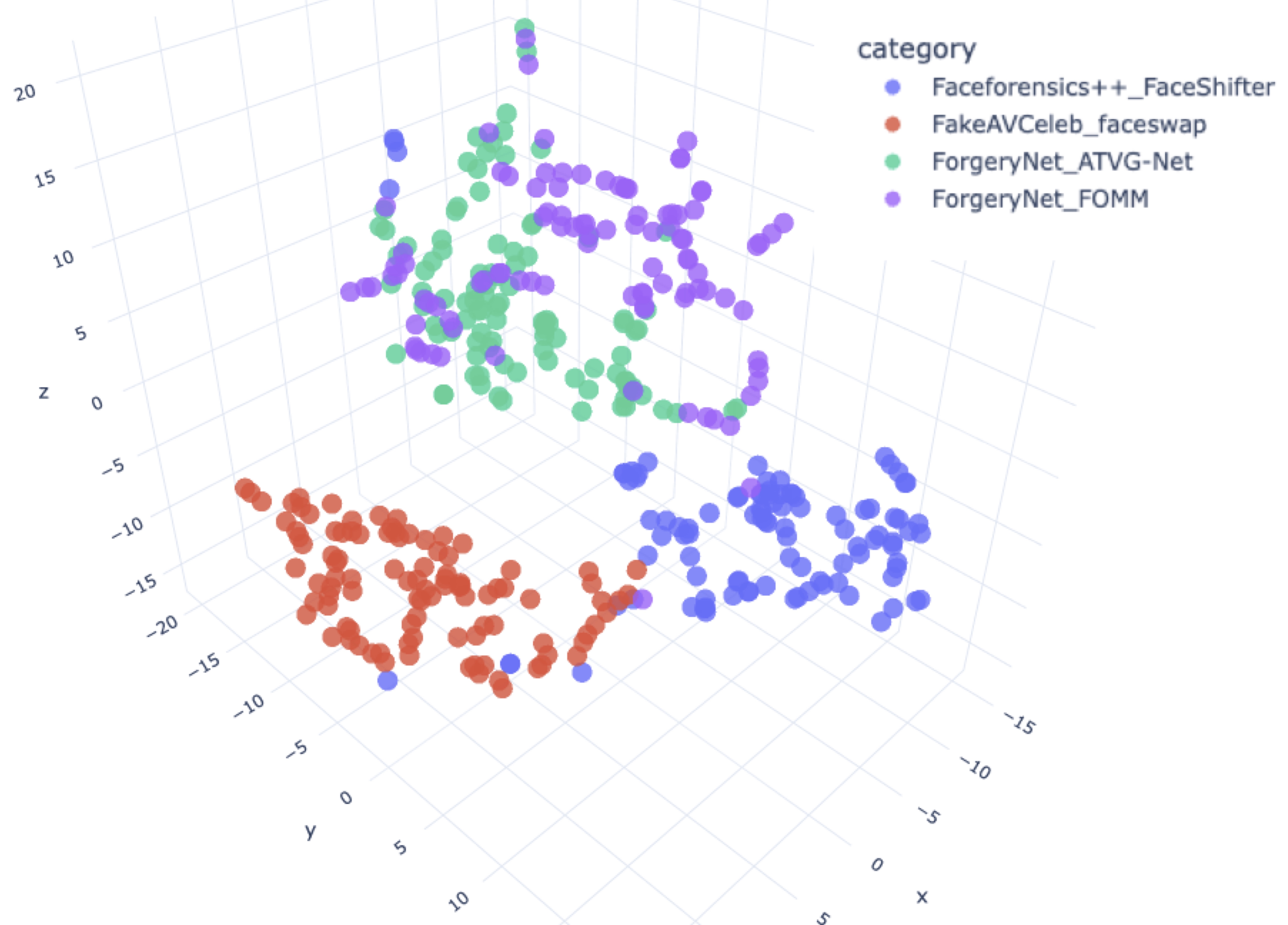
Figure 6. The model output of the evaluation sets, that be reduced to three dimensions using the t-SNE method for display.

Evaluating the performance of models trained with unreliably labeled or unlabeled data is difficult. We can not use precision and recall because we do not have a way to figure out whether each sample is classified correctly. To address this issue, we utilize the Calinski Harabasz Index [19], introduced by Calinski and Harabasz in 1974, as an effective evaluation method. This index is defined in Equation (1) as the ratio of the sum of between cluster dispersion and inter-cluster dispersion for all clusters. Therefore, the Calinski Harabasz Index can be used to evaluate the models, with higher scores indicating that the model performs better on the test datasets.

For a set of data 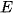of size 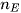, which has been clustered into 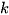clusters, the Calinski Harabasz score s is defined as the ratio of the between-cluster dispersion means and the within-cluster dispersion, as shown in Equation 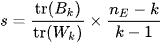(1).

                                    (1)

where 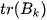is trace of the between group dispersion matrix and is the trace of the within-cluster dispersion matrix defined by:

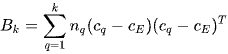                       (2)

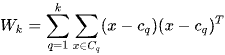                        (3)

Here, 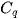represents the set of points in cluster, 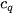represents the center of cluster 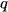, represents the center of 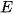, and 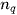represents the number of points in cluster .

When using the Calinski Harabasz Index to evaluate clustering quality, it can be observed that the elbow points of the Calinski Harabasz Index tend to be around 3 or 4 of cluster number, as depicted in Figure 7. The results obtained from the Calinski Harabasz Index are consistent with the number of forged method categories in the actual evaluation set. This suggests that the Calinski Harabasz Index is a valuable method to assess the model’s ability to identify new categories of deepfakes. When other training parameters remain the same, if a model’s performance is outstanding, it indicates that the quality of the training set is excellent, with fewer incorrect labels. In other words, we effectively improve the reliability of these classification labels in the training set. Therefore, the Calinski Harabasz Index can effectively evaluate the correlation of these unreliable classification labels in our system.

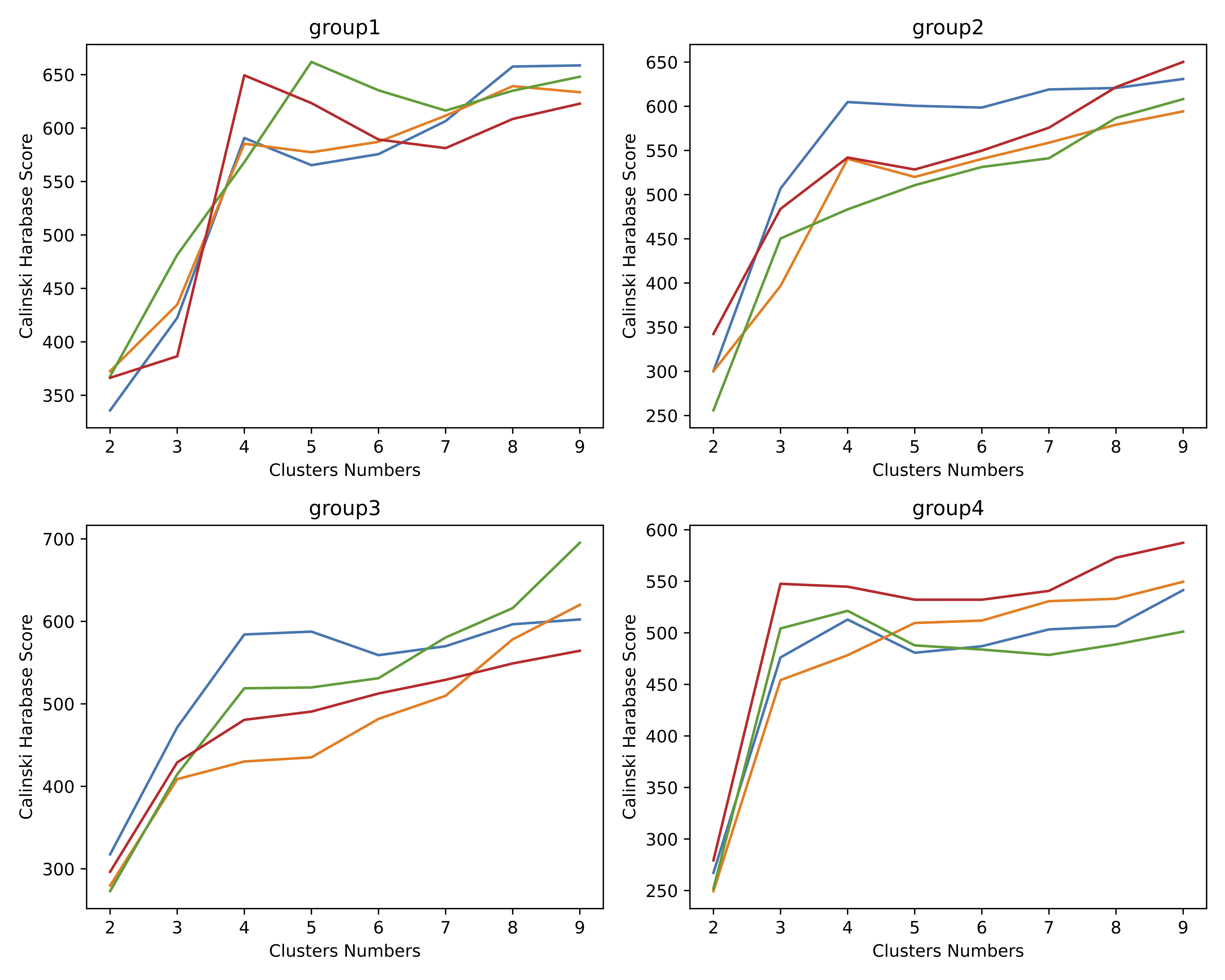
Figure 7. Using Calinski Harabasz Index to evaluate its clustering quality, it can be found that its elbow point is about 3 to 4.

4. Experiment

In this section, we first introduce the overall experimental setup. Our equipment includes four NVIDIA GeForce2080Ti GPUs. We use PyTorch to train and evaluate models, OpenCV to image data preprocessing, and Scikit-learn algorithm library for data analysis. We extract 620,000 fake face images from 10 deepfake datasets and train 40 models, including 32 Xception, 4 F3-net, and 4 ResNet models. The entire data preparation and experimental process spanned approximately 3 months.

4.1. Data Dividing and Preprocessing

We select 31 datasets labeled with forgery method names from CelebDF, DeeperForensics1.0, DeepFakeMnist+, FaceForensics++, ForgeryNet, and FakeAVCeleb, see Table 1 for details. We use a random method to divide 31 deepfake categories into two sets, where the training set contains 27 categories, and the evaluation set contains four categories. We repeat the above division four times to obtain four sets of training sets and evaluation sets. See Table 2 for details.

Table 2. The table displays four sets of experimental data, each containing four evaluation datasets, with the remaining 27 datasets designated for training purposes.

Group Evaluation Datasets
1 Faceforensics++_FaceShifter, FakeAVCeleb_FaceSwap, ForgeryNet_ATVG-Net, ForgeryNet_FOMM
2 DeeperForensics_DF-VAE, Faceforensics++_Face2Face, FakeAVCeleb_Wav2Lip, ForgeryNet_DiscoFaceGAN
3 DeepfakeTIMIT_FaceSwap-GAN, ForgeryNet_BlendFace, ForgeryNet_StarGAN2, Patch-wise-Face-Image-Forensics _PROGAN
4 CelebDFv2_FaceSwapPRO, Faceforensics++_ NeuralTextures, ForgeryNet_FS-GAN, ForgeryNet_Talking Head Video

We extract the frame data of each category according to the instructions of the relevant dataset and use the face detection model Retinaface [54] to intercept the face area. Then, we increase the side length of the image by a factor of 1.25. Finally, we randomly select 20,000 fake faces of each category and save these images as test data in png format.

4.2. Merge Training Data Based on the Category Name

To verify our conjecture that there is large randomness in the naming of the forged methods in the deepfake dataset, we specially merged the training set data according to the principle of the same or close to the forged method names and used them as a control group. We use the following merging rules.

  1.  Merge the FaceSwapPRO category in the CelebDFv1 dataset and the FaceSwapPRO category in the CelebDFv2 dataset. 
  2.  Merge the FOMM category in the DeepFakeMnist+ dataset and the FOMM category in the ForgeryNet dataset.
  3.  Merge the FaceSwap-GAN category in the DeepfakeTIMIT dataset, the DeepFakeDetection FaceSwap category and the FaceSwap category in the FaceForensics++ dataset, and the faceswap category in the FakeAVCeleb dataset.
  4.  Merge the DeepFakes category in the Faceforensics++ dataset and the DeepFakes category in the ForgeryNet dataset.
  5.  Merge the FSGAN category in the FakeAVCeleb dataset and the FS-GAN category in the ForgeryNet dataset.
  6.  Merge DeepFakes-StarGAN-Stack category, StarGAN-BlendFace-Stack category and StarGAN2 category in ForgeryNet dataset.
  7.  Merge the StyleGAN2 category in the ForgeryNet dataset and the STYLEGAN2 category in the Patch-wise Face Image Forensics dataset.

We randomly sample corresponding proportions of data from the merged dataset and reassemble them into 20,000 images per category. The number of training set categories of the merged four groups is that Group 1 has a total of 19 categories, Group 2 has a total of 17 categories, Group 3 has a total of 19 categories, and Group 4 has a total of 19 categories.

4.3. Merge Training Data Based on the Results of K-Means Clustering

One of the purposes of our experiment is to determine the appropriate dimensionality for K-means clustering to address this type of problem. We need to ensure that we do not lose too many classification features due to excessive dimensionality reduction, nor do we cause the K-means algorithm to fail due to excessive dimensionality. Since we chose the Xception model as the baseline, we use the PCA algorithm to reduce the 2048-dimensional output to 128, 64, and 32 dimensions. We also reduce it to two dimensions using the t-SNE algorithm. For the F3-net and ResNet models, we only use the PCA algorithm to reduce the output feature value to 64 dimensions since we only need to verify that our method applies to these models.

In the previous section, we created training data for the control group based on name mergers. To facilitate comparison, we ensure that the number of categories of the experimental data for each group is identical. Therefore, we use the K-means clustering algorithm to cluster these training sets based on the specified number of clusters. Groups 1, 3, and 4 have 19 clusters, while Group 2 has 17 clusters. Finally, we use the results of the K-means clustering algorithm to combine the training set.

4.4. Experimental Results

We train Xception, F3-net, and ResNet models using training data merged by K-means clustering results and category names, respectively. For comparison, we also train the same models using the original training set without merging.

To obtain feature vectors for the validation set, we used these models as feature extractors and applied PCA to reduce them to 64 dimensions. We then calculated the Calinski Harabasz Index. Please refer to Table 3 for the result.

Table 3. The Calinski Harabasz Index results. Italicized and underlined marks indicate the best result for that group of tests.

Model Train Data Merge by Group 1 CH Group 2 CH Group 3 CH Group 4 CH Avg CH
Xception Without merging 128.02825 117.448499 68.6994684 93.5723306 101.937137
Xception Name 84.0837009 73.8172086 74.579957 61.2651927 73.4365148
Xception K-means on 2048D 124.241305 105.070655 76.2218761 84.212058 97.4364735
Xception K-means on t-SNE 2D 103.627829 87.1461055 66.6143003 76.5264273 83.4786656
Xception K-means on PCA 64D 137.241584 101.192327 85.2535376 94.2137508 104.4753
Xception K-means on PCA 128D 101.197038 101.502163 74.8441997 86.6358341 91.0448087
Xception K-means on PCA 32D 114.247635 89.1934801 62.3932779 75.9596147 85.4485019
F3-net Name     62.6592813 65.6510862 64.1551837
F3-net K-means on PCA 64D     85.361067 72.018708 78.6898875
ResNet Name     42.895651 47.9716533 45.4336522
ResNet K-means on PCA 64D     49.7529116 54.0786263 51.915769

The Calinski Harabasz Index of the model trained on the data merged by K-means is 42.27% higher than that pooled by name. Furthermore, these scores are slightly higher than those directly using the original training set, even though the original set contains more data. At the same time, the Calinski Harabasz Index is also higher at 22.66% and 14.27% in F3-net and ResNet models. These prove an appropriate combination of deepfake datasets with similar features improves the model’s generalization in the unknown forgery categories.

The Calinski Harabasz Index of the model trained on the data merged by K-means is 42.27% higher than that pooled by name. Furthermore, these scores are slightly higher than those directly using the original training set, even though the original set contains more data. At the same time, the Calinski Harabasz Index is also higher at 22.66% and 14.27% in F3-net and ResNet models. These prove an appropriate combination of deepfake datasets with similar features improves the model’s generalization in the unknown forgery categories.

Compared with the other three groups, the results of Group 2 are different. Furthermore, its Calinski Harabasz Index is lower than the training results on the original data. Because Group 2 has only 17 categories after the merger, with fewer training samples than other groups. More information loss can destroy the performance of the model.

5. Conclusions

This article starts with the traceability requirements of the deep forgery method. When using multiple deepfake datasets, we found many different deepfake datasets using the same or similar label names. Confusion arises in how to use these datasets comprehensively.

We leverage the Xception model to extract fake features from the deepfake dataset. Subsequently, PCA and t-SNE methods are employed to reduce dimensionality and perform K-means clustering. Then, combine the datasets based on the clustering results, and use the combined data to train Xception, F3-net, and ResNet models, respectively. Finally, we use these models to extract features from the evaluation set and evaluate the generalization of these models using the Calinski Harabasz index as an evaluation metric. Our contributions are mainly three-fold:

  • We prove the labels of various deepfake datasets contain many randomnesses. If researchers use more than two deepfake datasets, combining these datasets only based on forgery labels will hurt the performance of the model.
  • We propose K-means and Calinski Harabasz evaluation systems to evaluate the similarity of various deepfake datasets, laying the foundation for future researchers to use them comprehensively.
  • We prove that the generalization ability of the deepfake recognition model in the face of new samples can be improved by merging datasets with high forgery feature similarity.

Our research is only a helpful exploration for entirely using various deep forgery datasets from the source of deep forgery methods. We mainly revealed the arbitrariness of label naming in deepfake datasets and the resulting troubles in the traceability of forgery methods. There is still a long way to go to solve this problem completely. In addition, different image compression algorithms and image resolutions significantly impact the fake features of deepfake datasets, which will seriously interfere with the model’s extraction of fake features from deepfake datasets, and pose a significant challenge to the identifiability and traceability of deepfake datasets. We are committed to conducting further research to address these challenges effectively.

To ensure the healthy development of the field, research institutions and universities should standardize the label nomenclature of deepfake datasets. Additionally, legislation should require digital watermarking and blockchain technology to accurately trace deepfake content to its source. Our research is a helpful exploration of the use of various deep forgery datasets, and we hope it will inspire future work in this field.

This entry is adapted from the peer-reviewed paper 10.3390/electronics12112353

References

  1. Korshunov, P.; Marcel, S. Deepfakes: A new threat to face recognition? assessment and detection. arXiv 2018, arXiv:1812.08685.
  2. Chesney, B.; Citron, D. Deep fakes: A looming challenge for privacy, democracy, and national security. Calif. L. Rev. 2019, 107, 1753.
  3. Dixon, H.B., Jr. Deepfakes: More Frightening Than Photoshop on Steroids. Judges’ J. 2019, 58, 35–37.
  4. Feldstein, S. How Artificial Intelligence Systems Could Threaten Democracy. Available online: https://scholarworks.boisestate.edu/pubadmin_facpubs/102/ (accessed on 20 December 2022).
  5. Verdoliva, L. Media forensics and deepfakes: An overview. IEEE J. Sel. Top. Signal Process. 2020, 14, 910–932.
  6. Xiang, Z.; Horváth, J.; Baireddy, S.; Bestagini, P.; Tubaro, S.; Delp, E.J. Forensic analysis of video files using metadata. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 1042–1051.
  7. Qureshi, A.; Megías, D.; Kuribayashi, M. Detecting deepfake videos using digital watermarking. In Proceedings of the 2021 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Tokyo, Japan, 14–17 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1786–1793.
  8. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144.
  9. Qian, Y.; Yin, G.; Sheng, L.; Chen, Z.; Shao, J. Thinking in frequency: Face forgery detection by mining frequency-aware clues. In Proceedings of the European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 86–103.
  10. Torralba, A.; Fergus, R.; Freeman, W.T. 80 million tiny images: A large data set for nonparametric object and scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1958–1970.
  11. Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Institute of Electrical and Electronics Engineers. Miami, FL, USA, 20–25 June 2009; pp. 248–255.
  12. Griffin, G.; Holub, A.; Perona, P. Caltech-256 Object Category Dataset. Available online: https://authors.library.caltech.edu/7694/ (accessed on 12 January 2023).
  13. Schwarz, H.; Marpe, D.; Wiegand, T. Overview of the scalable video coding extension of the H. 264/AVC standard. IEEE Trans. Circuits Syst. Video Technol. 2007, 17, 1103–1120.
  14. He, Y.; Gan, B.; Chen, S.; Zhou, Y.; Yin, G.; Song, L.; Sheng, L.; Shao, J.; Liu, Z. Forgerynet: A versatile benchmark for comprehensive forgery analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Institute of Electrical and Electronics Engineers, Virtual, 19–25 June 2021; pp. 4360–4369.
  15. Huang, J.; Wang, X.; Du, B.; Du, P.; Xu, C. DeepFake MNIST+: A DeepFake Facial Animation Dataset. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1973–1982.
  16. Khalid, H.; Tariq, S.; Kim, M.; Woo, S.S. FakeAVCeleb: A novel audio-video multimodal deepfake dataset. arXiv 2021, arXiv:2108.05080.
  17. Jiang, L.; Li, R.; Wu, W.; Qian, C.; Loy, C.C. Deeperforensics-1.0: A large-scale dataset for real-world face forgery detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2889–2898.
  18. Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1800–1807.
  19. Cali ́ nski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat.-Theory Methods 1974, 3, 1–27.
  20. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778.
  21. Rossler, A.; Cozzolino, D.; Verdoliva, L.; Riess, C.; Thies, J.; Nießner, M. Faceforensics++: Learning to detect manipulated facial images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–11.
  22. Li, Y.; Yang, X.; Sun, P.; Qi, H.; Lyu, S. Celeb-df: A large-scale challenging dataset for deepfake forensics. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 3207–3216.
  23. Lee, J. This Dataset Is a Summary of the Datasets Used in the “A Study on Patch-Wise Deepfake Image Detection” Experiment Presented at the Winter Conference of the Korean Society of Telecommunications. Available online: https://github.com/Jeonghan57/A-Study-on-Patch-Wise-Deepfake-Image-Detection (accessed on 20 December 2022).
  24. Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114.
  25. Korshunova, I.; Shi, W.; Dambre, J.; Theis, L. Fast face-swap using convolutional neural networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3677–3685.
  26. Nirkin, Y.; Keller, Y.; Hassner, T. Fsgan: Subject agnostic face swapping and reenactment. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 7184–7193.
  27. Prajwal, K.; Mukhopadhyay, R.; Namboodiri, V.P.; Jawahar, C. A lip sync expert is all you need for speech to lip generation in the wild. In Proceedings of the 28th ACM International Conference on Multimedia, New York, NY, USA, 12–16 October 2020; pp. 484–492.
  28. Siarohin, A.; Lathuilière, S.; Tulyakov, S.; Ricci, E.; Sebe, N. First order motion model for image animation. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc: Red Hook, NY, USA, 2019; Volume 32.
  29. Bshaoanlu. Faceswap-GAN. Available online: https://github.com/shaoanlu/faceswap-GAN (accessed on 12 January 2023).
  30. Kowalski, M. FaceSwap. Available online: https://github.com/MarekKowalski/FaceSwap/ (accessed on 12 January 2023).
  31. Deepfakes. Available online: https://github.com/deepfakes/faceswap (accessed on 9 January 2023).
  32. Thies, J.; Zollhofer, M.; Stamminger, M.; Theobalt, C.; Nießner, M. Face2face: Real-time face capture and reenactment of rgb videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2387–2395.
  33. Li, L.; Bao, J.; Yang, H.; Chen, D.; Wen, F. Faceshifter: Towards high fidelity and occlusion aware face swapping. arXiv 2019, arXiv:1912.13457.
  34. Thies, J.; Zollhöfer, M.; Nießner, M. Deferred neural rendering: Image synthesis using neural textures. ACM Trans. Graph. (TOG) 2019, 38, 1–12.
  35. Dufour, N.; Andrew Gully, J. Contributing Data to Deepfake Detection Research. Available online: https://ai.googleblog.com/2019/09/contributing-data-to-deepfake-detection.html (accessed on 25 December 2022).
  36. Chen, L.; Maddox, R.K.; Duan, Z.; Xu, C. Hierarchical cross-modal talking face generation with dynamic pixel-wise loss. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 7832–7841.
  37. Deng, Y.; Yang, J.; Chen, D.; Wen, F.; Tong, X. Disentangled and controllable face image generation via 3d imitative-contrastive learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5154–5163.
  38. Lee, C.H.; Liu, Z.; Wu, L.; Luo, P. Maskgan: Towards diverse and interactive facial image manipulation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5549–5558.
  39. Jo, Y.; Park, J. Sc-fegan: Face editing generative adversarial network with user’s sketch and color. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1745–1753.
  40. Choi, Y.; Uh, Y.; Yoo, J.; Ha, J.W. Stargan v2: Diverse image synthesis for multiple domains. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 8188–8197.
  41. Viazovetskyi, Y.; Ivashkin, V.; Kashin, E. Stylegan2 distillation for feed-forward image manipulation. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 170–186.
  42. Fried, O.; Tewari, A.; Zollhöfer, M.; Finkelstein, A.; Shechtman, E.; Goldman, D.B.; Genova, K.; Jin, Z.; Theobalt, C.; Agrawala, M. Text-based editing of talking-head video. ACM Trans. Graph. (TOG) 2019, 38, 1–14.
  43. Gao, H.; Pei, J.; Huang, H. Progan: Network embedding via proximity generative adversarial network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 4–8 August 2019; pp. 1308–1316.
  44. Chen, Z.; Yang, H. Attentive semantic exploring for manipulated face detection. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1985–1989.
  45. Liu, H.; Li, X.; Zhou, W.; Chen, Y.; He, Y.; Xue, H.; Zhang, W.; Yu, N. Spatial-phase shallow learning: Rethinking face forgery detection in frequency domain. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 772–781.
  46. Li, J.; Xie, H.; Li, J.; Wang, Z.; Zhang, Y. Frequency-aware discriminative feature learning supervised by single-center loss for face forgery detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 6454–6463.
  47. Guarnera, L.; Giudice, O.; Battiato, S. Deepfake detection by analyzing convolutional traces. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2841–2850.
  48. Liu, Z.; Qi, X.; Torr, P.H. Global texture enhancement for fake face detection in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 8060–8069.
  49. Yang, T.; Huang, Z.; Cao, J.; Li, L.; Li, X. Deepfake Network Architecture Attribution. Proc. AAAI Conf. Artif. Intell. 2022, 36, 4662–4670.
  50. Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108.
  51. Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. Density-based spatial clustering of applications with noise. In Proceedings of the International Conference Knowledge Discovery and Data Mining, Portland, Oregon, 2–4 August 1996; Volume 240, pp. 11–30.
  52. Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417.
  53. Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Academic Video Service
Feedback