Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Jessie Wu and Version 1 by Elango Lakshmanan.
Ant-inspired metaheuristic algorithms known as ant colony optimization (ACO) offer an approach that has the ability to solve complex problems in both discrete and continuous domains. ACOs have gained significant attention in the field of water resources management, since many problems in this domain are non-linear, complex, challenging and also demand reliable solutions.
- ant colony optimization (ACO)
- combinatorial optimization problems
- hydrology
- hydrogeology
1. Introduction
Applications of ant colony optimization (ACO) with respect to hydrology and hydrogeology include irrigation water allocation, urban drainage network design, groundwater long-term monitoring, reservoir optimization, watershed management, coastal aquifer management, hydraulic parameters stimulation and water distribution systems (Figure 1).
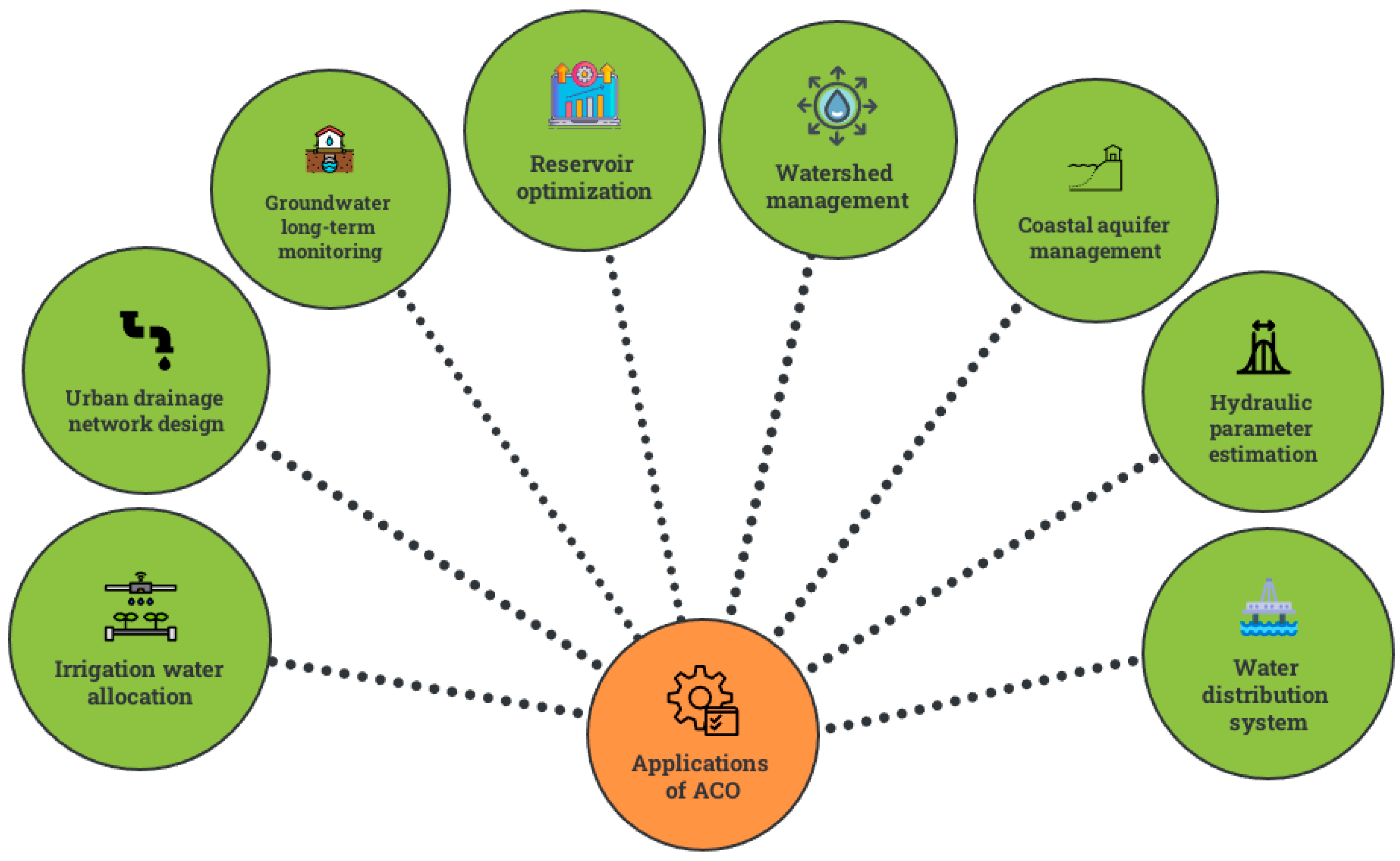
Figure 1.
Applications of ACO in hydrology and hydrogeology.
2. Reservoir Optimization
Reservoir optimization is important to attain the paramount possible performance of a reservoir system [43,44][1][2]. It helps in arriving at decisions pertaining to storage over a period of time and release from reservoirs, taking into consideration the variations in inflows and demands. There are many studies that compare the applications of the traditional ACO algorithm to GAs in solving reservoir operations problems (Table 1). ACO was applied for optimizing operations of Hirakud Reservoir, which is a multi-purpose reservoir system situated in Orissa, India, and identifies that ACO outperforms genetic algorithms in arriving at global-optimum solution for long-time horizon reservoir operation [45][3]. An improved ACO algorithm helped in refining the estimates of the optimal releases of the Dez Reservoir, as compared to the GAs, while the improvised ACO algorithm needs fine tuning of the parameters to arrive at expected results [46][4]. Moeini et al. [46][4] proposed a modified ant colony algorithm to determine optimal reservoir operation for continuous domains (ACOR). This algorithm was applied to the Dez Reservoir in southern Iran, and the performance has been compared to GAs. The main disadvantage of ACO algorithm is the enormous computer runtime, so an efficient methodology to decrease the runtime has been developed in this restudyearch. The same CACO algorithm for multi-reservoir parameter optimization has been used by [46][4]. Three different formulations of ACO, such as partially constrained ACO algorithm, max–min ant system, and fully constrained ACO algorithm were used to solve fourteen reservoir operation problems, and these techniques are compared to the conventional ACO algorithm. It was inferred that the new modified ACO techniques have an upper hand when compared to the traditional ACO algorithm to solve large-scale multi-reservoir operation problems [47][5] and can be used for solving complex water resource problems. CACO algorithm was used to determine a set of control parameters to identify the optimal operation of the Dez Reservoir. It is stated that CACO gave a good performance for global minimization of continuous test functions. A normalized squared deviation of the releases from the desired demands was assigned as the fitness function. In this restudyearch, CACO algorithm was compared with the solution obtained by DACO models and nonlinear programming (NLP) models. The CACO model is superior to the NLP and DACO models as they provide an alternative to the tedious trial and error-based approach by adopting an elitist strategy [48][6]. It is inferred that the previously experienced difficulty in substantiating the computational efforts required to execute an ant colony-based optimization problem has been resolved by some researchers; however, the techniques to overcome difficulties faced while parameter tuning are yet to be addressed seriously by researchers.
Table 1.
ACO for reservoir operations.
| Year | ACO Variant | Application | Name of the Reservoir | Reference |
|---|---|---|---|---|
| 2006 | Improved ACO | Single purpose | Dez Reservoir, Iran | [43][1] |
| 2006 | ACO | Multi-purpose | Hirakud Reservoir, India | [45][3] |
| 2008 | ACO for continuous domains | Single purpose | Dez Reservoir, Iran | [44][2] |
| 2013 | CACOA, UCACO, PCACO, FCACO, max –min ant system | Multi-purpose | Theoretical study | [46][4] |
| 2018 | CACO & DACO | Single purpose | Dez Reservoir, Iran | [47][5] |
3. Water Distribution Systems
Several studies have been dedicated to the improvement of techniques to optimize the capital costs allied to water distribution system (WDS) infrastructure (Table 2). Although traditional linear and nonlinear techniques have been used to solve many WDS optimization issues, for a constrained minimization problem, variants of ACO have been fruitful in managing the trade-off between various conflicting attributes [48][6]. A significant aspect of WDS network design is to find the optimum network layout that satisfies power consumption, pressure, and also minimizes cost while meeting a performance criterion. In their research, Simpson et al. [49][7] have studied with 14 pipes and have tried to optimize the WDS using different combinations of parameters. Global optimum solutions were achieved, and the sensitivity of the ACO algorithm performance has been analyzed using the optimal range for six parameters. The drawback of this technique is that experience is required to decide which parameter needs to be selected, but an alternate method that helps in deciding which parameter needs to be selected is lacking. [50][8]. Two benchmark WDS optimization problems were considered and budgeting for the two were studied. The findings of this restudy earch revealed that ACO algorithms can be considered as an alternative to GAs for finding near global optimal solutions and also computational efficiency [50][8]. The cost solutions mentioned in previous literature are not practically possible since they seem to be violating the minimum pressure constraints while studying using EPANET [51][9]. The ACO parameters were explained better by developing parametric guidelines for the application of ACO to WDS optimization using an ACO variant known as ASi-best, since it uses an iteration-best pheromone updating scheme [50][8]. It is observed that ASi-best provides the best efficiency and solution quality for the New York Tunnels problem but is only partially satisfactory for the Hanoi problem [51][9]. On the other hand, in order to understand the searching behavior of ants, their behavior was characterized into three categories: (i) searching behavior for feasible and infeasible regions, (ii) effective search for arriving at optimal or near-optimal regions of the search space, and (iii) the algorithm exploration extent as it converges to solutions. Variants of ACOs were tested under these conditions, including how internal operators affect each algorithm’s searching behavior [52][10].
A comparison between the performances of five ant colony algorithms was conducted to study the efficiency in optimization for WDS [52][10]. The algorithms are EAS, ACS, MMAS, and Elitist-ASrank. It was observed that MMAS and ASrank outperform all the other ant colony optimization techniques available, particularly in minimizing the design costs of WDS. The drawback is that the restudy earch has been carried out only for systems that are mentioned in the literature, but no real time applications have been carried out yet to check the validity of the results. While looking at the application of ACOs for various WDS applications, there are a lot of convincing results and satisfactory observations, but most of them have been conducted based on literature data, and real-time applications are not available. Further, studies involving the sensitivity of ACOAs to the parameters are few, and scenarios where ACOAs should be used in preference to GAs are not very convincing. To overcome this, a real water distribution network of El-Mostakbal City, Egypt, to determine the least-cost design was applied and determined that ACO is suitable only for simple networks, while PSO is the best for complex designs and they converge to the best solution [53][11]. In a parallel study for two typical canal irrigation systems in China, ACO algorithms yielded reduced leakage loss of delivered water from 7.29% to 5.40%, and 8.97% to 7.46% [54,55][12][13]. In order to optimize scheduled water delivery under water shortage conditions from an irrigation canal in Iran, applications of ACO were compared with Fuzzy SARSA learning model (FSL) [56][14]. The FSL method outperformed ACO method under three emergency operations and also led to less maximum absolute error (MAE) and integral of absolute magnitude of error (IAE) in comparison to the ACO method.
Table 2.
ACO for WDS.
| Year | ACO Variant | Application | Reference | ||||
|---|---|---|---|---|---|---|---|
| 2001 | ACO | Parameter selection | [49][7] | ||||
| ] | 2003 | ACO | Optimal design | [ | |||
| 2009 | 50 | ] | ACDE[8] | ||||
| Water resource problems | [ | 68 | ][26] | 2005 | ACO, ASi-best | Optimal design | [51][9] |
| Spatial evaluation of water quality | [ | 59 | ][17] | ||||
| 2010 | ECACO | Seawater intrusion management | [69][27] | 2012 | ACO | Metric analysis for ACO search behavior | [52][10] |
| 2016 | Modified ACO | Flow modelling | [60][18] | ||||
| 2021 | |||||||
| 2012 | ACO + SWAT | Non-point source pollution management | [70][28] | 2014 | Elitist AS, AS, ERAS, MMAS | Minimize design cost | [53][11] |
| ACOR | Water quality management | 2017 | EA, GA, PSO, ACO, MA | Design and rehabilitation | [54][12] | ||
| 2018 | ACO | Planning of water delivery schedules | [55][13] | ||||
| 2020 | Fuzzy SARSA learning and ACO | Water delivery scheduling under water shortage conditions | [56][14] |
4. Hydrogeological Parameter Estimation
Studying movement of water, drinking water quality, transmissivity, storage coefficient and water level are of some important hydrogeological parameters that are instrumental in setting up environmental policies (Figure 2 and Table 3). A hybrid ACO algorithm to identify the storage coefficient and transmissivity for a two-dimensional, unsteady state groundwater flow model has been used [57][15]. Hybrid ACO algorithms are more advantageous in applications of gradient-based optimization methods [57][15]. This is mainly because ACO algorithms are global search algorithms and possess the ability to identify a parameter set in a stable manner. As an added advantage, this restudy earch has successfully formulated an optimization problem for parameter identification in an inverse problem [58][16].

Figure 2.
Variants of ACO for hydrogeological parameter optimization.
ACO algorithms have the ability to search for a globally optimal solution. Hence, for estimating optimum permeability ACO has been used in Mansuri Bangestan Reservoir located in Ahwaz, Iran [58][16]. A hybrid ACO algorithm along with back propagation algorithm (ACA-BP) was used to fasten the evolution of neural networks and improve its forecasting precision. The available geophysical well log data was made use of, and it is proposed that ACA-BP yields better results than using the BP algorithm alone. However, while using this methodology, it is reported that identification of optimal neural network topology is strenuous, and the validity of these results when compared to the already proven GAs do not have any valid proof [58][16].
Since drinking water quality is an important parameter, [59][17] reported an evaluation method for spatial evaluation of drinking water quality by using GIS and ant colony clustering algorithm. This method integrates ACCA along with geographical information system (GIS). Strategies such as probability conversion functions, average similitude degree, and mixed distance function were used to improvise an ACCA algorithm. Various water quality grades were developed using ACCA in the GIS environment. The results derived from ACCA were compared with competitive Hopfield neural network (CHNN). The spatial water quality grades obtained from ACCA possess the upper hand when compared to CHNN [59][17]. Since spatial water quality assessment is an important parameter, it is very important that wresearchers make maximum use of this intelligent methodology. This methodology takes into consideration over 35 parameters, and hence it can be considered a valid procedure for evaluating water quality.
A methodology to assess the movement of water in the unsaturated media has been studied, where the ACO algorithm has been used extensively since it is a metaheuristic approach [60][18]. As metaheuristic approaches require parameters to be differentiable or continuous, ABACOA is preferred, especially because they have not used gradient or Hessian matrix from classic optimization. A modified ACO algorithm estimates Mualem-van Genuchten unsaturated hydraulic soil parameters for vadose zone using a sequential fitting. Inferring from the above studies it can be concluded that there is a future scope for estimation of parameters in inverse problems for groundwater hydrology. ACOR is coupled with ANFIS (ANFIS-ACOR) and used to study spatial salinity distribution. ACO is being widely coupled with machine learning algorithms to predict soil salinity in different environmental conditions and prediction of groundwater salinity [61][19]. Electrical resistivity imaging is used to reconstruct a conductivity model of subsurface water-bearing bodies. A priori constrained improved ACO algorithm for 3-D resistivity inversion was observed to be good at controlling search direction and improving inversion efficiency [62][20]. The efficacy of ACOs has been positively harnessed in combination with Fuzzy logic as well as the recently developing machine learning models such as neural networks, support vector regression, etc. in optimizing parameters in water quality simulation model, simulating of discharge, and evapotranspiration. ACOs, when compared to other optimizing algorithms, offered increased accuracy and better performance [63,64,65,66][21][22][23][24].
Table 3.
ACO for hydraulic and hydrogeological parameters.
| Year | ACO Variant | Application | Reference |
|---|---|---|---|
| 2006 | Hybrid ACO | Transmissivity and storage co-efficient for unsteady groundwater flow | [57][15] |
| 2012 | ACO-BP | Permeability analysis | [58][16] |
| 2014 | ACCO | ||
| [ | |||
| 61 | ] | [ | 19] |
| 2022 | Improved ACO | Earth resistivity | [62][20] |
5. Other Applications
ACO and its variants are also used for other applications in water resources management. A brief description of those applications are described in this section (refer Table 4).
Table 4.
ACO for other applications in water resources.
| Year | ACO variant | Application | Reference | ||
|---|---|---|---|---|---|
| ] | |||||
| [ | |||||
| 22 | |||||
| ] | |||||
| 2006 | ACO-LTM | Groundwater long-term monitoring | [67][ | ||
| 2016 | |||||
| ABACO-TGA | Urban drainage network design | [ | 71][29] | ||
| 2018 | ACO | Water management in irrigation areas | [72][30] | ||
| 2022 | ACO | Groundwater salinity | [63][21] | ||
| 2022 | ACO | River water level forecasting | [ | ||
| 2023 | ACO | Evapotranspiration | [65][23] | ||
| 25 | 64 | 2023 | ACO | Discharge | [66][24] |
5.1. Long-Term Groundwater Monitoring
ACO has been incorporated to develop a methodology that optimizes long-term monitoring (LTM) of groundwater to help monitor human health risk at post-closure sites where contaminants are still present and to study the performance of groundwater remediation [67][25]. A set of redundant sampling locations was identified by the ACO-LTM algorithm, and global optimal or near-optimal solutions were determined. This algorithm has been applied to a small network comprising 30 wells; however, it needs to be applied to large-scale field sites, and it requires temporal optimization of a long-term monitoring network.
5.2. ACDE-Water Resources Problems
5.2. Ant Colony-Coupled-Differential Evolution-Water Resources Problems
ACO coupled with differential evolution for solving a few real-time water resources problems such as water pumping system formulation, parameter estimation of water quality model, etc. was studied. To overcome the slow convergence rate and large computational time required for optimization of objective function, differential evolution was coupled with ACO to develop a modified algorithm known as ant colony-coupled-differential evolution (ACDE) [62][20]. ACDE was validated for two real-life problems, and also for a test bed of seven benchmark problems. As aimed, the computational effort was reduced, and the global optimal solution was attained without compromising the quality of the solution. ACDE algorithm also outperformed other algorithms in solving a few real-life problems [68][26].
5.3. Coastal Aquifer Management–Salt Water Intrusion
ECACO algorithm was used for optimal control variable management of a coastal aquifer to control saltwater intrusion. ECACO was used for maximizing the total water-pumping rate as well as simultaneously controlling the drawdown limits and protecting the wells from saltwater intrusion. In addition, a numerical simulation approach was combined with an ECACO algorithm to study potential applicability of the model for optimal management of a coastal aquifer [69][27]. Although this restudy earch gave reasonable results, there was more scope for integrating the proposed methodology approach, with already commercially available simulation tools. This study research was carried out for a complex aquifer; however, only preliminary studies were conducted. With saltwater intrusion being an alarming issue of the hour, the maximum potential of variants of ACOs are yet to be utilized by researchers.
5.4. Non-Point Source Pollution Management–Watershed Management
ACO algorithm was applied on a breakthrough watershed management methodology. The ultimate aim of this restudy earch was to practice cost allocation among landowners in a watershed and control the total sediment yield in the watershed. The problem of non-point source pollution management in watershed scale reached a feasible solution as ACO algorithm helped in decision making without any additional computational burden. ACO coupled with a SWAT model helped in selecting optimum decision vectors [70][28]. Hence, they can help landowners to optimally control the sediment release from basins in pre and post development conditions and reach payoffs.
5.5. Urban Drainage and Storm Network Design
Sewer networks play crucial roles in human protection and environmental health management. Hence, it is very important to solve sewer network design optimization problems. ACO and its variants were coupled with an appropriate hydraulic simulator in a simulation-optimization framework, taking into consideration inter-network effects such as surcharge and backwater, and reduced simplification of system representation. ACO algorithms were also successfully used to optimize the management of stormwater retention tanks. Studies suggest that heuristic approaches solve large-scale sewer network design optimization problems better when compared to other methods. ACO algorithms augmented with tree growing algorithms (TGA) resulted in efficient estimation of network design and they are known as ABACOA [71][29]. Verdaguer et al. [71][29] have used both constrained and unconstrained versions of ABACOA algorithms to determine the nodal cover depths of sewer pipes, by considering the pipe slope. This is mainly because of the incremental solution building capability of the ACO algorithms. Constrained ABACOA-TGA produced better results with the same computational effort [71][29]. This technique appears to always be feasible for arriving at a minimum slope constraint. Further research and development are necessary in this area of water distribution system by considering design efficiency, multiple objectives, integrated design, risks and uncertainties, and constraint performance-based design. Applications of ACO algorithms in the area of urban drainage and stormwater network design has still not gained popularity and importance.
5.6. Optimal Crop and Irrigation Water Allocation
An improved ACO formulation for the allocation of crops and water to different irrigation areas enables dynamic decision variable option adjustment and utilizes domain knowledge to bias the search towards selecting crops that give maximum net returns and water allocations that result in the largest net return for the selected crop, given a fixed total volume of water [72][30]. The use of visibility factors optimized the ability to identify better solutions at all stages of the search, especially at smaller events of function evaluations. Hence, using ACO to identify near-optimal solutions for detailed irrigation scheduling for individual crops is better than the computationally costly, mechanistic crop growth models.
References
- Jalali, M.R.; Afshar, A.; Marino, M.A. Improved Ant Colony Optimization Algorithm for Reservoir Operation. Sci. Iran 2006, 13, 295–302.
- Kumar, D.N.; Reddy, M.J. Ant Colony Optimization for Multi-Purpose Reservoir Operation. Water Resour. Manag. 2006, 20, 879–898.
- Dariane, A.B.; Moradi, A.M. Reservoir Operating by Ant Colony Optimization for Continuous Domains (ACOR) Case Study: Dez Reservoir. Int. J. Math. Phys. Eng. Sci. 2009, 3, 2.
- Moeini, R.; Afshar, M.H. Extension of the constrained ant colony optimization algorithms for the optimal operation of multi-reservoir systems. J. Hydroinf. 2013, 15, 155–173.
- Mohammad, A.; Ketabchi, H.; Rasa, E. Elitist Continuous Ant Colony Optimization Algorithm: Application to Reservoir Operation Problems. Int. J. 2006, 4, 274–285.
- Sarbu, I.; Popa-Albu, S. Optimization of urban water distribution networks using heuristic methods: An overview. Water Int. 2022, 48, 120–148.
- Simpson, A.R.; Maier, H.R.; Foong, W.K. Selection of parameters for ant colony optimization applied to the optimal design of water distribution systems. In Proceedings of the International Congress on Modelling and Simulation, Canberra, Australia, 10–13 December 2001; Australian National University: Perth, WA, Australia, 2001; pp. 1931–1936.
- Maier, H.R.; Simpson, A.R.; Zecchin, A.C.; Foong, W.K.; Phang, K.Y.; Seaha, H.Y.; Tan, C.L. Ant colony optimization for design of water distribution systems. J. Water Resour. Plan. Manag. 2003, 129, 200–208.
- Zecchin, A.C.; Simpson, A.R.; Maier, H.R.; Nixon, J.B. Parametric study for an ant algorithm applied to water distribution system optimization. IEEE Trans. Evol. Comput. 2005, 9, 175–191.
- Zecchin, A.C.; Simpson, A.R.; Maier, H.R. Improved understanding of the searching behavior of ant colony optimization algorithms applied to the water distribution design problem. Water Resour. Res. 2012, 48, 1–16.
- Zecchin, A.C.; Maier, H.R.; Simpson, A.R. Ant Colony Optimization Applied to Water Distribution System Design: Comparative Study of Five Algorithms. J. Water Resour. Plan. Manag. 2007, 133, 87–92.
- El-Ghandour, H.A.; Elbeltagi, M.E. Comparison of Five Evolutionary Algorithms for Optimization of Water Distribution Networks. J. Comput. Civil Eng. 2018, 32. Available online: https://ascelibrary.org/doi/abs/10.1061/%28ASCE%29CP.1943-5487.0000717 (accessed on 1 February 2023).
- Liu, Y.; Yang, T.; Zhao, R.-H.; Li, Y.-B.; Zhao, W.-J.; Ma, X.-Y. Irrigation Canal System Delivery Scheduling Based on a Particle Swarm Optimization Algorithm. Water 2018, 10, 1281.
- Omidzade, F.; Ghodousi, H.; Shahverdi, K. Comparing Fuzzy SARSA Learning and Ant Colony Optimization Algorithms in Water Delivery Scheduling under Water Shortage Conditions. J. Irrig. Drain. Eng. 2020, 146. Available online: https://ascelibrary.org/doi/10.1061/%28ASCE%29IR.1943-4774.0001496 (accessed on 1 February 2023).
- Li, S.; Liu, Y.; Yu, H. Parameter Estimation Approach in Groundwater Hydrology Using Hybrid Ant Colony System. In Computational Intelligence and Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 182–191.
- Irani, R.; Nasimi, R. An evolving neural network using an ant colony algorithm for a permeability estimation of the reservoir. Pet. Sci. Technol. 2011, 30, 375–384.
- Hou, J.W.; Mi, W.B.; Li, L.T. Spatial quality evaluation for drinking water based on GIS and ant colony clustering algorithm. J. Cent. South Univ. 2014, 21, 1051–1057.
- Dobre, G.; Drobot, R. Estimating soil hydraulic parameters using a metaheuristic algorithm. Model. Civil Eng. 2011, 102–111.
- Ghorbani, M.K.; Afshar, A.; Hamidifar, H. River water quality management using a fuzzy optimization model and the NSFWQI Index. Water SA 2021, 47, 45–53.
- Guo, Q.; Wang, H.; Bai, J.; Liu, B.; Wu, H.; Wu, Z.; He, Z. A Priori Constrained ACO Method Applied to Three-Dimensional Imaging of Subsurface Electrical Resistivity. Geotech. Geol. Eng. 2023, 41, 15–25.
- Jamei, M.; Karbasi, M.; Malik, A.; Abualigah, L.; Islam, A.R.M.T.; Yaseen, Z.M. Computational assessment of groundwater salinity distribution within coastal multi-aquifers of Bangladesh. Sci. Rep. 2022, 12, 11165.
- Ahmed, A.A.M.; Deo, R.C.; Ghahramani, A.; Feng, Q.; Raj, N.; Yin, Z.; Yang, L. New double decomposition deep learning methods for river water level forecasting. Sci. Total Environ. 2022, 831, 154722.
- Ghorbani, M.K.; Afshar, A.; Hamidifar, H.; Reddy, M.J. Proceedings of the Institution of Civil Engineers. Water Manag. 2022, 175, 190–205.
- Eslamitabar, V.; Ahmadi, F.; Sharafati, A.; Rezaverdinejad, V. Bivariate simulation of river flow using hybrid intelligent models in sub-basins of Lake Urmia, Iran. Acta Geophys. 2023, 71, 873–892.
- Li, Y.; Chan Hilton, A.B. Reducing Spatial Sampling in Long-Term Groundwater Monitoring Networks Using Ant Colony Optimization. Int. J. Comput. Intell. Res. 2010, 1, 19–28.
- Ali, M.; Pant, M.; Abraham, A. A Hybrid Ant Colony Differential Evolution and its application to water resources problems. In Proceeding of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 1133–1138.
- Ataie-Ashtiani, B.; Ketabchi, H. Elitist Continuous Ant Colony Optimization Algorithm for Optimal Management of Coastal Aquifers. Water Resour. Manag. 2010, 25, 165–190.
- Skardi, M.J.E.; Afshar, A.; Solis, S.S. Simulation-optimization model for non-point source pollution management in watersheds: Application of cooperative game theory. KSCE J. Civ. Eng. 2013, 17, 1232–1240.
- Verdaguer, M.; Clara, N.; Gutiérrez, O.; Poch, M. Application of Ant-Colony-Optimization algorithm for improved management of first flush effects in urban wastewater systems. Sci. Total Environ. 2014, 485–486, 143–152.
- Nguyen, D.C.H.; Dandy, G.C.; Maier, H.R.; Ascough, J.C., II. Improved Ant Colony Optimization for Optimal Crop and Irrigation Water Allocation by Incorporating Domain Knowledge. J. Water Resour. Plan. Manag. 2016, 142. Available online: https://ascelibrary.org/doi/10.1061/%28ASCE%29WR.1943-5452.0000662 (accessed on 1 February 2023).
More
