Machine Learning-Based Forecasting of Renewable Energy: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Rita Xu and Version 1 by Natei Ermias Benti.

With the increasing penetration of renewable energy sources (RES) into the electricity grid, accurate forecasting of their generation becomes crucial for efficient grid operation and energy management. Traditional forecasting methods have limitations, and thus ML and DL algorithms have gained popularity due to their ability to learn complex relationships from data and provide accurate predictions.

  • energy management
  • renewable energy forecasting
  • deep learning

1. Introduction

Renewable energy research and development have gained significant attention due to a growing demand for clean and sustainable energy in recent years [1][2]. In the fight to cut greenhouse gas emissions and slow down climate change, renewable energy is essential [3][4][5]. In addition, renewable energy sources (RES) offer several advantages, including a reduction in energy dependence on foreign countries, job creation, and the potential for cost savings [1][6]. However, the inherent variability and uncertainty of RES present a significant challenge for the widespread adoption of renewable energy [7][8]. For example, wind energy generation is heavily influenced by the weather, which can be unpredictable and difficult to forecast accurately [9][10]. Similarly, solar energy generation is influenced by factors such as cloud cover and seasonal changes in sunlight [11]. The high variability and uncertainty of renewable energy generation make it challenging to integrate RES into the power grid efficiently [12].
One approach to addressing this challenge is to develop accurate forecasting models for renewable energy generation. Accurate forecasting models can help minimize the negative impact of the variability and uncertainty of renewable energy generation on the power grid. For decades, energy generation has been predicted using traditional forecasting models, such as statistical and physical models [13]. However, statistical models such as the autoregressive integrated moving average (ARIMA) method have limitations in their ability to handle complex nonlinear relationships and the high-dimensional nature of renewable energy data [14]. Physical models, such as numerical weather prediction (NWP) models and solar radiation models, are widely used for renewable energy forecasting. NWP models use atmospheric data to predict wind speed and direction, while solar radiation models use cloud cover and atmospheric conditions to predict solar irradiance. However, these models have limitations due to the complexity of the Earth’s atmosphere and the inherent uncertainty in weather forecasting. Improving these models’ accuracy requires ongoing research and development to address these limitations [15][16]. Promising approaches to address the limitations of traditional forecasting models involve the utilization of ML and DL algorithms [14]. ML and DL algorithms can learn complex nonlinear relationships from immense quantities of information, making them suitable for handling the high-dimensional nature of renewable energy data. Moreover, they can handle a wide range of input data types, including time series data, meteorological data, and geographical data.
Many researchers have looked at the application of ML and DL algorithms for the forecasting of solar radiation, a significant element influencing the output power of solar systems [17]. For instance, Voyant et al. suggested the use of hybrid models (HMs) to enhance prediction performance after discovering that SVR, SVM, ARIMA, and ANN are the superior approaches for forecasting solar radiation [18]. Huertas et al. demonstrated that the HM with SVM outperformed single predictor models in terms of improving forecasts of solar radiation [19]. In comparison to other models, Gürel et al. discovered that the ANN algorithm was the most effective model for assessing solar radiation [20]. Alizamir et al. found that when predicting solar radiation, the GBT model outperforms other models in terms of accuracy and precision [21]. Srivastava et al. suggest that the four ML algorithms (CART, MARS, RF, and M5) can be utilized for forecasting hourly solar radiation for up to six days in advance, with RF demonstrating the best performance while CART showing the weakest performance [22]. In their study, Agbulut et al. demonstrated that the various ML algorithms they tested were highly accurate in predicting daily global solar radiation data, with the best performance achieved by the ANN algorithm [23].
Similar to solar energy, the prediction of wind energy poses a challenge due to its nonlinearity and randomness, which results in inconsistent power generation. Consequently, there is a need for an effective model to forecast wind energy, as evidenced by research studies [24][25]. In light of the rising global population and increasing energy demand, wind energy is viewed as a feasible alternative to depleting fossil fuels. Offshore wind farms are particularly advantageous compared to onshore wind farms since they offer higher capacity and access to more wind sources [26]. ML and DL models and algorithms are employed in wind energy development, utilizing wind speed data and other relevant information. Various researchers have proposed different models to increase prediction accuracy. For example, Zendehboud et al. suggested the SVM model as superior to other models and introduced hybrid SVM models [27]. Wang et al. proposed an HM comprising a combination of models for short-term wind speed prediction [28]. Demolli et al. used five ML algorithms to predict long-term wind power, finding that the SVR algorithm is most effective when the standard deviation is removed from the dataset [29]. Xiaoetal suggested using a self-adaptive kernel extreme learning machine (KELM) as a means to enhance the precision of forecasting [30]. The ARIMA and nonlinear autoregressive exogenous (NARX) models were evaluated by Cadenas et al., who concluded that the NARX model had less error [31]. Wind power and speed were predicted in other studies using a variety of models, including the improved dragonfly algorithm (IDA) with SVM (IDA–SVM) model, local mean decomposition (LMD), firefly algorithm (FA) models, and the CNN model [15][32][33].
ML and DL have significantly advanced the field of forecasting renewable energy. However, there are still several issues that need to be resolved. For instance, the choice of ML and DL algorithms, the selection of input data, and the handling of missing data are essential factors that affect the precision of forecasting models for renewable energy. Additionally, there is a need to develop robust and interpretable models that can provide insights into the factors that influence renewable energy generation.

2. Machine Learning-Based Forecasting of Renewable Energy

2.1. Supervised Learning

ML is a subset of artificial intelligence that seeks to enable machines to learn from data and improve their ability to perform a particular task [34][35]. The process involves developing statistical models and algorithms that enable computers to identify patterns in data and utilize them to make decisions or predictions. In essence, ML involves teaching a computer to identify and react to specific types of data by presenting it with extensive examples, known as “training data.” This training procedure helps the computer identify patterns and make predictions or decisions based on fresh data that it has not encountered previously [36][37][38]. The applications of ML span diverse industries such as healthcare, finance, e-commerce, and others [39][40][41][42][43][44]. In addition, ML techniques can be leveraged for predicting renewable energy generation, resulting in better management of renewable energy systems with improved efficiency and effectiveness. There are multiple ML algorithms available, each with distinct strengths and weaknesses. The algorithms can be categorized into three primary groups: supervised learning, unsupervised learning, and reinforcement learning [45]. Supervised learning refers to a ML method that involves training a model using data that has been labeled. The labeled data comprises input-output pairs, where the input is the data on which the model is trained and the output is the expected outcome [46][47]. The model learns to map inputs to outputs by reducing the error between the predicted and actual outputs during training. Once trained, the model can be applied to generate predictions on new, unlabeled data [48][49]. Regression and classification are the two basic sub-types of supervised learning algorithms (Figure 1) [46].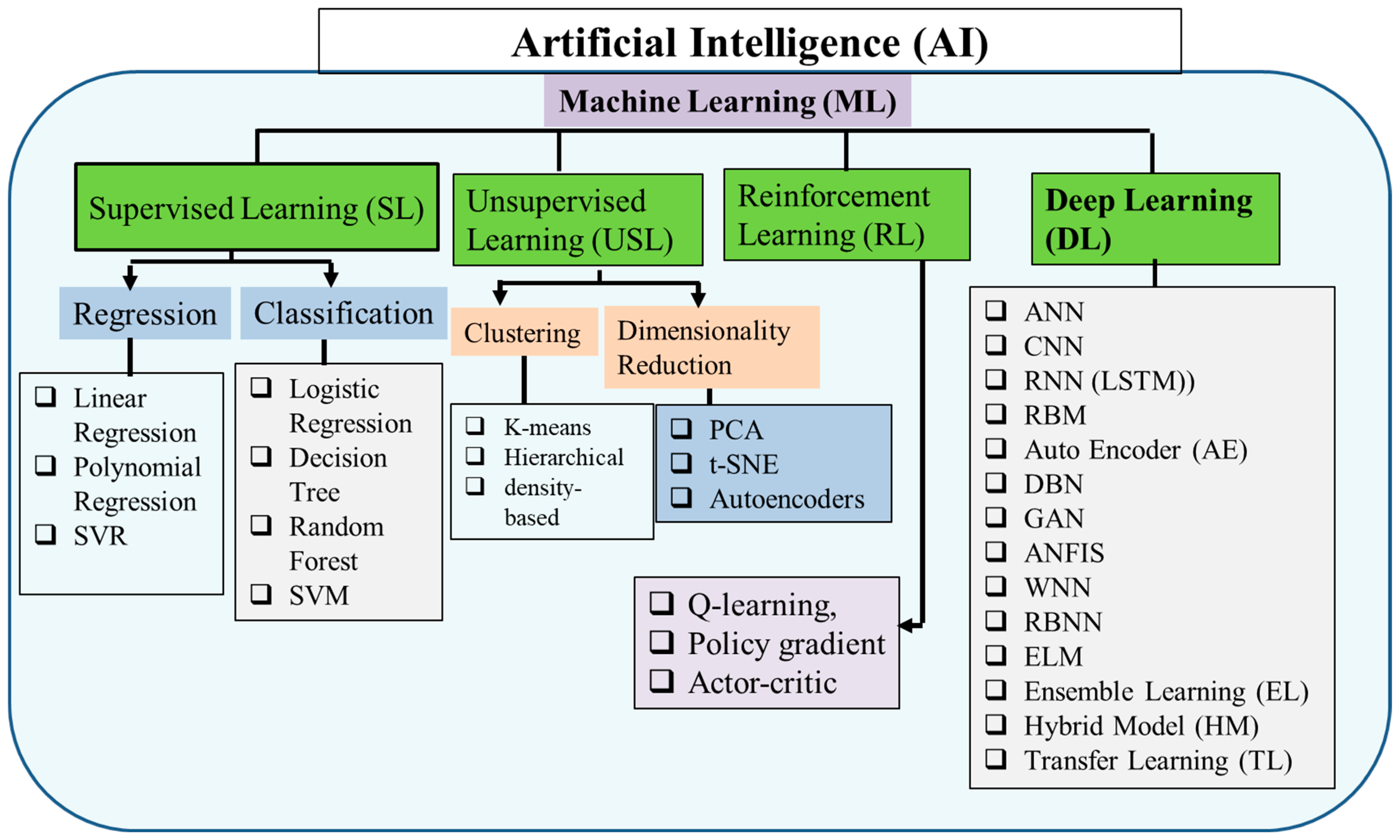
Sustainability 15 07087 g001
Figure 1. ML types and algorithms.
Table 1 presents a comparative analysis of various ML and DL algorithms, outlining their respective advantages and disadvantages across different applications.
Table 1. ML and DL Technics with pros and cons in different applications.
Technique Pros Cons Applications
Linear Regression Easy to implement, fast training Limited to linear relationships Predictive analytics
Logistic Regression Interpretable, works well with small datasets Assumes linearity, apply only for classification Predict power outages, classify extreme weather events, market, and healthcare
Decision Trees Interpretable, can handle both categorical and continuous data Prone to overfitting Predictive maintenance, finance
Random Forest High accuracy, less prone to overfitting Computationally expensive compared to DT, difficult to interpret Operation control strategy, image classification, and fraud detection
SVM Can handle high-dimensional data, can handle non-linear relationships, robust to noise Computationally expensive and requires careful parameter tuning Text classification, bioinformatics
K-means clustering Simple and fast, useful for data exploration and segmentation Requires a pre-determined number of clusters and can be sensitive to initial conditions Market segmentation, image segmentation
PCA Can reduce dimensionality and noise in data, useful for data exploration and visualization May not capture all relevant information and can be difficult to interpret Image and speech recognition, natural language processing
Reinforcement Learning Can learn through trial and error, useful for decision-making in dynamic environments Requires a lot of data and can be prone to overfitting Game playing, robotics
ANN Can learn complex relationships, handle large datasets, and model non-linear relationships Requires large amounts of data and can be difficult to interpret Predict energy demand (stationary), energy resource forecasting, image recognition, and speech recognition
CNN Highly effective for image analysis, it can learn features automatically Requires large amounts of data, is computationally expensive, may not be suitable for low spatial or temporal resolutions Object detection, image classification, and predicting energy demand based on satellite images of areas
RNN Can handle sequential data and time series data and can handle long-term dependencies Can be prone to overfitting and slow training, and may suffer from vanishing or exploding gradients Energy price forecasting (time series), speech recognition, and sentiment analysis
LSTM Can handle long-term dependencies, which is useful for time series data Can be prone to overfitting and require careful tuning Time series, speech recognition, natural language processing, load forecasting, and energy price forecasting (time series)
Autoencoders Can reduce dimensionality and noise in data and be used for unsupervised learning Requires large amounts of data and can be difficult to interpret Anomaly detection, image, and speech recognition
ELM Fast training, can handle large datasets Limited interpretability may not generalize well to new data Renewable energy forecasting, image and speech recognition, predictive analytics
GRNN Fast training and can handle noise in data Limited to regression tasks and may not scale well to large datasets Renewable energy forecasting, time series prediction, and function approximation
RBNN Effective for non-linear regression and classification tasks Requires careful tuning of network architecture and hyperparameters Image and speech recognition, anomaly detection
WNN Can handle multi-resolution and multi-scale data Requires careful selection of wavelet basis functions and can be computationally expensive Image and signal processing, time series prediction
ANFIS Can handle uncertainty and non-linearity in data Requires careful selection and tuning of fuzzy rules and can be computationally expensive Control systems, fault diagnosis
DBN Can learn hierarchical representations of data, which is effective for unsupervised learning Requires large amounts of data, can be difficult to interpret Image and speech recognition, natural language processing
Ensemble Learning Can improve performance and reduce overfitting by combining multiple models Can be computationally expensive and may require careful tuning Renewable energy forecasting, image and speech recognition, and natural language processing
Transfer Learning Can leverage pre-trained models to improve performance and require less data May not generalize well to new data, limited to similar tasks Load forecasting, energy price prediction, predictive maintenance, fault diagnosis, energy consumption, energy efficiency forecasting, renewable energy foresting, image and speech recognition, and natural language processing
1. Regression: Regression is a supervised learning approach that forecasts a continuous output variable based on one or more input variables. Regression aims to identify a mathematical function that can correlate the input variables to a continuous output variable, which may represent a single value or a range of values [50]. Linear regression, polynomial regression, and support vector regression (SVR) are the three main types of supervised learning algorithms in regression [51]. Linear and Polynomial Regression: Linear regression is a prevalent and straightforward approach used to forecast a continuous output variable utilizing one or more input variables. It uses a straight line to indicate the correlation between the input variables and the output variables [52]. On the other hand, polynomial regression, a type of linear regression, employs nth-degree polynomial functions to depict the connection between input features and the outcome variable [53]. This can enhance the accuracy of predictions by enabling the model to capture more intricate correlations between the input data and the target variable. In renewable energy forecasting, both linear and polynomial regression can be used to predict the power output of RES such as solar and wind power [54][55]. Weather information such as temperature, humidity, and wind speed are frequently included in the input characteristics, along with historical power output data. The target variable is the power output of the renewable energy source, which can be predicted using the input features. For instance, Ibrahim et al. (2012) used data from a weather station collected over three years to create a linear regression model to predict solar radiation in Perlis. The model used three input variables (average daily maximum and minimum temperatures, as well as the average daily solar radiation) and had a good fit with an R-squared value of 0.954. The authors concluded that their model could be a useful tool for estimating solar radiation in Perlis [56]. Ekanayake et al. (2021) created artificial neural networks (ANNs), multiple linear regression, and power regression models to produce wind power prediction models for a Sri Lankan wind farm. In their modeling approach, they utilized climate parameters such as average wind speed and average ambient temperature as input variables for their analysis. The models were developed using power generation data over five years and showed acceptable accuracy with low RMSE, low bias, and a high correlation coefficient. The ANN model was the most precise, but the MLR and PR models provide insights for additional wind farms in the same area [57]. Mustafa et al. (2022) also compared four regression models, linear regression, logistic regression, Lasso regression, and elastic regression, for solar power prediction. The results showed that all four models are effective, but the elastic regression outperformed the others in predicting maximum solar power output. Principal component analysis (PCA) was also applied, showing improved results in the elastic regression model. The paperntry focuses on the strengths and weaknesses of each solar power prediction model [58]. Support Vector Regression (SVR): The SVR algorithm is utilized in regression analysis within the field of ML [59]. It works by finding the best hyperplane that can separate the data points in a high-dimensional space. The selection of the hyperplane aims to maximize the distance between the closest data points on each side of it. The approach involves constraining the margin while minimizing the discrepancy between the predicted and actual values. It is also a powerful model to predict renewable energy potential for a specific location. For example, Yuan et al. (2022) proposed a jellyfish search algorithm optimization SVR (IJS-SVR) model to predict wind power output and address grid connection and power dispatching issues. The SVR was optimized using the IJS technique, and the model was tested in both the spring and winter. IJS-SVR outperformed other models in both seasons, providing an effective and economical method for wind power prediction [60]. In addition, Li et al. (2022) created ML-based algorithms for short-term solar irradiance prediction, incorporating a hidden Markov model and SVM regression techniques. The Bureau of Meteorology demonstrated that their algorithms can effectively forecast solar irradiance for 5–30 min intervals in various weather conditions [61]. Mwende et al. (2022) developed SVR and random forest regression (RFR) models for real-time photovoltaic (PV) power output forecasting. On the validation dataset, SVR performed better than RFR with an RMSE of 43.16, an adjusted R2 of 0.97, and a MAE of 32.57, in contrast to RFR’s RMSE of 86, an adjusted R2 of 0.90, and a MAE of 69 [62]. 2. Classification: Classification, a form of supervised learning, involves using one or more input variables to anticipate a categorical output variable [63]. Classification aims to find a function that can map the input variables to discrete output categories. The most widely used classification algorithms for predicting RES include logistic regression, decision trees, random forests, and support vector machines. Logistic Regression: Logistic regression is a classification method that utilizes one or more input variables to forecast a binary output variable [64][65]. It models the probability of the output variable being true or false using a sigmoid function. In renewable energy forecasting, logistic regression can be used to predict whether or not a specific event will occur, such as a solar or wind farm reaching a certain level of power output. For instance, Jagadeesh et al. used ML to develop a forecasting method for solar power output in 2020. They used a logistic regression model with data from 11 months, including plant output, solar radiation, and local temperature. The study found that selecting the appropriate solar variables is essential for precise forecasting. Additionally, it examined the algorithm’s precision and the likelihood of a facility generating electricity on a particular day in the future [66]. Decision Trees: An alternative classification method is decision trees, which involve dividing the input space into smaller sections based on input variable values and then assigning a label or value to each of these sections [65]. The different studies developed decision tree models to forecast power output from different renewable energy systems. Essama et al. (2018) developed a model to predict the power output of a photovoltaic (PV) system in Cocoa, Florida, USA, using weather parameters obtained from the United States National Renewable Energy Laboratory (NREL). By selecting the best performance among the ANN, RF, DT, extreme gradient boosting (XGB), and LSTM algorithms, they aim to fill a research gap in the area. They have concluded that even if all of the algorithms were good, ANN is the most accurate method for forecasting PV solar power generation. Random Forest: An effective and reliable prediction is produced by the supervised ML method known as random forest, which creates several decision trees and merges them [67]. The bagging technique, which is employed by random forests, reduces the variance of the base algorithms. This technique is particularly useful for forecasting time-series data [68]. Random forest mitigation correlation between trees by introducing randomization in two ways: sampling from the training set and selecting from the feature subset. The RF model creates a complete binary tree for each of the N trees in isolation, which enables parallel processing. Vassallo et al. (2020) investigate optimal strategies for random forest (RF) modeling in wind speed/power forecasting. The investigation examines the utilization of random forest (RF) as a corrective measure, comparing direct versus recursive multi-step prediction, and assessing the impact of training data availability. Findings indicate that RF is more efficient when deployed as an error-correction tool for the persistence approach and that the direct forecasting strategy performs slightly better than the recursive strategy. Increased data availability continually improves forecasting accuracy [69]. In addition, Shi et al. (2018) put forward a two-stage feature selection process, coupled with a supervised random forest model, to address overfitting, weak reasoning, and generalization in neural network models when forecasting short-term wind power. The proposed methodology removes redundant features, selects relevant samples, and evaluates the performance of each decision tree. To address the inadequacies of the internal validation index, a new external validation index correlated with wind speed is introduced. Simulation examples and case studies demonstrate the model’s better performance than other models in accuracy, efficiency, and robustness, especially for noisy data and wind power curtailment [70]. Similarly, Natarajan and Kumar (2015) also compared wind power forecasting methods. Physical methods rely on meteorological data and numerical weather prediction (NWP), while statistical methods such as ANN and SVM depend on historical wind speed data. This restudyearch experiments with the random forest algorithm, finding it more accurate than ANN for predicting wind power at wind farms [71]. Support Vector Machines (SVM): SVM are a type of classification algorithm that identifies a hyperplane and maximizes the margin between the hyperplane and the data points, akin to SVR [72][73]. SVM has been utilized in renewable energy forecasting to estimate the power output of wind and solar farms by incorporating input features such as historical power output, weather data, and time of day. For instance, Zeng et al. (2022) propose a 2D least-squares SVM (LS-SVM) model for short-term solar power prediction. The model uses atmospheric transmissivity and meteorological variables and outperforms the reference autoregressive model and radial basis function neural network model in terms of prediction accuracy [74]. R. Meenal and A. I. Selvakumar (2018) conducted studies comparing the accuracy of SVM, ANN, and empirical solar radiation models in forecasting monthly mean daily global solar radiation (GSR) in several Indian cities using varying input parameters. Using WEKA software, the authors determine the most significant parameters and conclude that the SVM model with the most influential input parameters yields superior performance compared to the other models [75]. Generally, classification algorithms are used to predict categorical output variables, and regression techniques are used to predict continuous output variables. The particular task at hand and the properties of the data will determine which method is used.

2.2. Unsupervised Learning

Another form of ML is unsupervised learning, where an algorithm is trained on an unlabeled dataset lacking known output variables, to uncover patterns, structures, or relationships within the data [76][77][78]. Unsupervised learning algorithms can be primarily classified into two types, namely clustering and dimensionality reduction [79]. Clustering: It is an unsupervised learning method that consists of clustering related data points depending on how close or similar they are to one another. Clustering algorithms, such as K-means clustering, hierarchical clustering, and density-based clustering, are commonly used in energy systems to identify natural groupings or clusters within the data. The primary objective of clustering is to discover these inherent patterns, or clusters [76][77]. K-means clustering is a widely used approach for dividing data into k clusters, where k is a user-defined number. Each data point is assigned to the nearest cluster centroid by the algorithm, and the centroids are updated over time using the average of the data points in the cluster [76][77]. Hierarchical clustering is also a family of algorithms that recursively merge or split clusters based on their similarity or distance to create a hierarchical tree-like structure of clusters. The other family of clustering algorithms that groups data points that are within a certain density threshold and separates them from areas with lower densities is the density-based clustering algorithm [76][77][78]. Dimensionality Reduction: It is also an unsupervised learning technique utilized to decrease the quantity of input variables or features while retaining the significant information or structure in the data [76][77][78]. The purpose of dimensionality reduction is to find a lower-dimensional representation of data that captures the majority of the variation or variance in the data. Principal component analysis (PCA), t-SNE, and autoencoders are some dimensionality reduction algorithms used in renewable energy forecasting [79]. Principal component analysis (PCA) is a commonly utilized method for decreasing the dimensionality of a dataset. It does so by identifying the primary components or directions that have the most variability in the data and then mapping the data onto these components [79]. t-SNE is a non-linear dimensionality reduction algorithm that is particularly useful for visualizing high-dimensional data in low-dimensional space. It uses a probabilistic approach to map similar data points to nearby points in low-dimensional space. Autoencoders are a type of neural network that can learn to encode and decode high-dimensional data in a lower-dimensional space. The encoder network is trained to condense the input data into a representation with fewer dimensions, and the decoder network is trained to reconstruct the original data from this condensed representation [79]. In general, unsupervised learning algorithms are particularly useful when there is a large amount of unstructured data that needs to be analyzed and when it is not clear what the specific target variable should be. Unsupervised learning has found various applications in the field of renewable energy forecasting, and one of its commonly used applications is the clustering of meteorological data [80]. For example, in a study by J. Varanasi and M. Tripathi (2019), K-means clustering was used to group days of the year, sunny days, cloudy days, and rainy days into clusters based on similarity for short-term PV power generation forecasting [81]. The resulting clusters were then used to train separate ML models for each cluster, which resulted in improved PV power forecasting accuracy. Unsupervised learning has also been used for anomaly detection in renewable energy forecasting. Anomaly detection refers to the task of pinpointing data points that exhibit notable deviations from the remaining dataset. In the context of renewable energy forecasting, anomaly detection can aid in identifying exceptional weather patterns or uncommon circumstances that may impact renewable energy generation. For example, in a study by Xu et al. (2015), the K-means algorithm was used to identify anomalous wind power output data, which was then employed to improve the accuracy of the wind power forecasting model [82]. In the realm of renewable energy forecasting, unsupervised learning has been utilized for feature selection, which involves choosing a smaller set of pertinent features from a larger set of input variables. In renewable energy forecasting, feature selection can be used to reduce the computational complexity of ML models and improve the accuracy of renewable energy output predictions. For example, in a study by Scolari et al. (2015), K-means clustering was used to identify a representative subset of features for predicting solar power output [83]. Overall, unsupervised learning is a powerful tool for analyzing large amounts of unstructured data in renewable energy forecasting. Clustering, anomaly detection, and feature selection are just a few of the many applications of unsupervised learning in this field, and new techniques are continually being developed to address the unique challenges of renewable energy forecasting.

2.3. Reinforcement Learning Algorithms

Reinforcement learning (RL) is a branch of ML in which an agent learns to make decisions in an environment to maximize a cumulative reward signal [84][85]. The agent interacts with its surroundings by taking actions and receiving responses in the form of rewards or penalties that are contingent on its actions. [86]. Some examples of RL algorithms are Q-learning, policy gradient, and actor-critic [87][88]. Q-learning is a RL algorithm used for learning optimal policies for decision-making tasks by iteratively updating the Q-values, which represent the expected future rewards for each action in each state [89]. Policy gradient is also a RL algorithm used for learning policies directly without computing the Q-values [90]. Actor-critic is another RL algorithm that combines elements of both value-based and policy-based methods by training an actor network to generate actions and a critic network to estimate the value of those actions [90]. Renewable energy forecasting is among the many tasks for which RL has been utilized [88][91]. One approach to applying RL to renewable energy forecasting is to use it to control the operation of energy systems [92]. For example, Sierra-García J. and S. Matilde (2020) developed an advanced yaw control strategy for wind turbines based on RL [93]. This approach uses a particle swarm optimization (PSO) and Pareto optimal front (PoF)-based algorithm to find optimal actions that balance power gain and mechanical loads, while the RL algorithm maximizes power generation and minimizes mechanical loads using an ANN. The strategy was validated with real wind data from Salt Lake City, Utah, and the NREL 5-MW reference wind turbine through FAST simulations [93].

2.4. Deep Learning (DL)

DL is a type of ML that employs ANNs containing numerous layers to acquire intricate data representations with multiple layers of abstraction. The term “deep” refers to the large number of layers in these ANNs, which can range from a few layers to hundreds or even thousands of layers [94]. DL algorithms can learn to recognize patterns and relationships in data through a process known as “training.” During training, the weights of the links between neurons in an ANN are changed to reduce the disparity between the anticipated and actual output [95]. DL has brought about significant transformations in several domains, such as energy systems, computer vision, natural language processing, speech recognition, and autonomous systems. It has facilitated remarkable advancements in various fields, such as natural language processing, game playing, speech recognition, and image recognition [80].

References

  1. Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50.
  2. Strielkowski, W.; Civín, L.; Tarkhanova, E.; Tvaronavičienė, M.; Petrenko, Y. Renewable Energy in the Sustainable Development of Electrical Power Sector: A Review. Energies 2021, 14, 8240.
  3. Tiruye, G.A.; Besha, A.T.; Mekonnen, Y.S.; Benti, N.E.; Gebreslase, G.A.; Tufa, R.A. Opportunities and Challenges of Renewable Energy Production in Ethiopia. Sustainability 2021, 13, 10381.
  4. Benti, N.E.; Woldegiyorgis, T.A.; Geffe, C.A.; Gurmesa, G.S.; Chaka, M.D.; Mekonnen, Y.S. Overview of geothermal resources utilization in Ethiopia: Potentials, opportunities, and challenges. Sci. Afr. 2023, 19, e01562.
  5. Benti, N.E.; Aneseyee, A.B.; Geffe, C.A.; Woldegiyorgis, T.A.; Gurmesa, G.S.; Bibiso, M.; Asfaw, A.A.; Milki, A.W.; Mekonnen, Y.S. Biodiesel production in Ethiopia: Current status and future prospects. Sci. Afr. 2023, 19, e01531.
  6. Benti, N.E.; Mekonnen, Y.S.; Asfaw, A.A. Combining green energy technologies to electrify rural community of Wollega, Western Ethiopia. Sci. Afr. 2023, 19, e01467.
  7. Kumar J., C.R.; Majid, M.A. Renewable energy for sustainable development in India: Current status, future prospects, challenges, employment, and investment opportunities. Energy Sustain. Soc. 2020, 10, 1–36.
  8. Denholm, P.; Arent, D.J.; Baldwin, S.F.; Bilello, D.E.; Brinkman, G.L.; Cochran, J.M.; Cole, W.J.; Frew, B.; Gevorgian, V.; Heeter, J.; et al. The challenges of achieving a 100% renewable electricity system in the United States. Joule 2021, 5, 1331–1352.
  9. Nazir, M.S.; Alturise, F.; Alshmrany, S.; Nazir, H.M.J.; Bilal, M.; Abdalla, A.N.; Sanjeevikumar, P.; Ali, Z.M. Wind generation forecasting methods and proliferation of artificial neural network: A review of five years research trend. Sustainability 2020, 12, 3778.
  10. Lledó, L.; Torralba, V.; Soret, A.; Ramon, J.; Doblas-Reyes, F. Seasonal forecasts of wind power generation. Renew. Energy 2019, 143, 91–100.
  11. Alhamer, E.; Grigsby, A.; Mulford, R. The Influence of Seasonal Cloud Cover, Ambient Temperature and Seasonal Variations in Daylight Hours on the Optimal PV Panel Tilt Angle in the United States. Energies 2022, 15, 7516.
  12. Impram, S.; Nese, S.V.; Oral, B. Challenges of renewable energy penetration on power system flexibility: A survey. Energy Strat. Rev. 2020, 31, 100539.
  13. Ghalehkhondabi, I.; Ardjmand, E.; Weckman, G.R.; Young, W.A. An overview of energy demand forecasting methods published in 2005–2015. Energy Syst. 2017, 8, 411–447.
  14. Krechowicz, A.; Krechowicz, M.; Poczeta, K. Machine Learning Approaches to Predict Electricity Production from Renewable Energy Sources. Energies 2022, 15, 9146.
  15. Hong, Y.-Y.; Satriani, T.R.A. Day-ahead spatiotemporal wind speed forecasting using robust design-based deep learning neural network. Energy 2020, 209, 118441.
  16. Zhao, X.; Liu, J.; Yu, D.; Chang, J. One-day-ahead probabilistic wind speed forecast based on optimized numerical weather prediction data. Energy Convers. Manag. 2018, 164, 560–569.
  17. Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Zeng, W.; Wang, X.; Zou, H. Empirical and machine learning models for predicting daily global solar radiation from sunshine duration: A review and case study in China. Renew. Sustain. Energy Rev. 2019, 100, 186–212.
  18. Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2016, 105, 569–582.
  19. Huertas-Tato, J.; Aler, R.; Galván, I.M.; Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Pozo-Vazquez, D. A short-term solar radiation forecasting system for the Iberian Peninsula. Part 2: Model blending approaches based on machine learning. Sol. Energy 2020, 195, 685–696.
  20. Gürel, A.E.; Ağbulut, Y.; Biçen, Y. Assessment of machine learning, time series, response surface methodology and empirical models in prediction of global solar radiation. J. Clean. Prod. 2020, 277, 122353.
  21. Alizamir, M.; Kim, S.; Kisi, O.; Zounemat-Kermani, M. A comparative study of several machine learning based non-linear regression methods in estimating solar radiation: Case studies of the USA and Turkey regions. Energy 2020, 197, 117239.
  22. Srivastava, R.; Tiwari, A.; Giri, V.; Srivastava, R.; Tiwari, A.; Giri, V. Solar radiation forecasting using MARS, CART, M5, and random forest model: A case study for India. Heliyon 2019, 5, e02692.
  23. Khosravi, A.; Koury, R.; Machado, L.; Pabon, J. Prediction of hourly solar radiation in Abu Musa Island using machine learning algorithms. J. Clean. Prod. 2018, 176, 63–75.
  24. Li, C.; Lin, S.; Xu, F.; Liu, D.; Liu, J. Short-term wind power prediction based on data mining technology and improved support vector machine method: A case study in Northwest China. J. Clean. Prod. 2018, 205, 909–922.
  25. Yang, W.; Wang, J.; Lu, H.; Niu, T.; Du, P. Hybrid wind energy forecasting and analysis system based on divide and conquer scheme: A case study in China. J. Clean. Prod. 2019, 222, 942–959.
  26. Lin, Z.; Liu, X. Wind power forecasting of an offshore wind turbine based on high-frequency SCADA data and deep learning neural network. Energy 2020, 201, 117693.
  27. Zendehboudi, A.; Baseer, M.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285.
  28. Wang, J.; Hu, J. A robust combination approach for short-term wind speed forecasting and analysis—Combination of the ARIMA (Autoregressive Integrated Moving Average), ELM (Extreme Learning Machine), SVM (Support Vector Machine) and LSSVM (Least Square SVM) forecasts using a GPR (Gaussian Process Regression) model. Energy 2015, 93, 41–56.
  29. Demolli, H.; Dokuz, A.S.; Ecemis, A.; Gokcek, M. Wind power forecasting based on daily wind speed data using machine learning algorithms. Energy Convers. Manag. 2019, 198, 111823.
  30. Xiao, L.; Shao, W.; Jin, F.; Wu, Z. A self-adaptive kernel extreme learning machine for short-term wind speed forecasting. Appl. Soft Comput. 2020, 99, 106917.
  31. Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Heard, C. Wind Speed Prediction Using a Univariate ARIMA Model and a Multivariate NARX Model. Energies 2016, 9, 109.
  32. Li, L.-L.; Zhao, X.; Tseng, M.-L.; Tan, R.R. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J. Clean. Prod. 2020, 242, 118447.
  33. Tian, Z. Short-term wind speed prediction based on LMD and improved FA optimized combined kernel function LSSVM. Eng. Appl. Artif. Intell. 2020, 91, 103573.
  34. Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260.
  35. Carbonell, J.G.; Michalski, R.S.; Mitchell, T.M. An Overview of Machine Learning. In Machine Learning: An Artificial Intelligence Approach; Morgan Kaufmann: Burlington, MA, USA, 1983; Volume 1.
  36. Wang, H.; Ma, C.; Zhou, L. A Brief Review of Machine Learning and its Application. In Proceedings of the International Conference on Information Engineering and Computer Science (ICIECS 2009), Wuhan, China, 19–20 December 2009; pp. 1–4.
  37. Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674.
  38. Alanne, K.; Sierla, S. An overview of machine learning applications for smart buildings. Sustain. Cities Soc. 2022, 76, 103445.
  39. Atienza, P.L.D.; Ogbechie, J.D.-R.A.; Bielza, C.P.-S.C. Industrial Applications of Machine Learning; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: New York, NY, USA, 2019.
  40. Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid- state materials science. Npj Comput. Mater. 2019, 5, 83.
  41. Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587.
  42. Kushwaha, S.; Bahl, S.; Bagha, A.K.; Parmar, K.S.; Javaid, M.; Haleem, A.; Singh, R.P. Significant Applications of Machine Learning for COVID-19 Pandemic. J. Ind. Integr. Manag. 2020, 5, 453–479.
  43. Recknagel, F. Applications of machine learning to ecological modelling. Ecol. Model. 2001, 146, 303–310.
  44. Valletta, J.J.; Torney, C.; Kings, M.; Thornton, A.; Madden, J. Applications of machine learning in animal behaviour studies. Anim. Behav. 2017, 124, 203–220.
  45. Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160.
  46. Liu, B. Exploring Hyperlinks, Contents, and Usage Data, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011.
  47. Miorelli, R.; Kulakovskyi, A.; Chapuis, B.; D’almeida, O.; Mesnil, O. Supervised learning strategy for classification and regression tasks applied to aeronautical structural health monitoring problems. Ultrasonics 2021, 113, 106372.
  48. Knudsen, E. Supervised learning in the brain. J. Neurosci. 1994, 14, 3985–3997.
  49. Sen, P.C.; Hajra, M.; Ghosh, M. Supervised Classification Algorithms in Machine Learning: A Survey and Review. In Emerging Technology in Modelling and Graphics; Advances in Intelligent Systems and Computing 937; Springer Nature: Singapore, 2020; pp. 99–111.
  50. Xie, S.; Liu, Y. Improving supervised learning for meeting summarization using sampling and regression. Comput. Speech Lang. 2010, 24, 495–514.
  51. Caruana, R. An Empirical Comparison of Supervised Learning Algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 161–168.
  52. Maulud, D.; AbdulAzeez, A.M. A Review on Linear Regression Comprehensive in Machine Learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147.
  53. Gambhir, E.; Jain, R.; Gupta, A.; Tomer, U. Regression Analysis of COVID-19 using Machine Learning Algorithms. In Proceedings of the 2020 International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 7–9 October 2020; pp. 65–71.
  54. Mahmud, K.; Azam, S.; Karim, A.; Zobaed, S.; Shanmugam, B.; Mathur, D. Machine Learning Based PV Power Generation Forecasting in Alice Springs. IEEE Access 2021, 9, 46117–46128.
  55. Elasha, F.; Shanbr, S.; Li, X.; Mba, D. Prognosis of a Wind Turbine Gearbox Bearing Using Supervised Machine Learning. Sensors 2019, 19, 3092.
  56. Ibrahim, S.; Daut, I.; Irwan, Y.; Irwanto, M.; Gomesh, N.; Farhana, Z. Linear Regression Model in Estimating Solar Radiation in Perlis. Energy Procedia 2012, 18, 1402–1412.
  57. Ekanayake, P.; Peiris, A.T.; Jayasinghe, J.M.J.W.; Rathnayake, U. Development of Wind Power Prediction Models for Pawan Danavi Wind Farm in Sri Lanka. Math. Probl. Eng. 2021, 2021, 4893713.
  58. Erten, M.Y.; Aydilek, H. Solar Power Prediction using Regression Models. Int. J. Eng. Res. Dev. 2022, 14, s333–s342.
  59. Ho, C.H.; Lin, C.J. Large-scale linear support vector regression. J. Mach. Learn. Res. 2012, 13, 3323–3348.
  60. Yuan, D.-D.; Li, M.; Li, H.-Y.; Lin, C.-J.; Ji, B.-X. Wind Power Prediction Method: Support Vector Regression Optimized by Improved Jellyfish Search Algorithm. Energies 2022, 15, 6404.
  61. Li, J.; Ward, J.K.; Tong, J.; Collins, L.; Platt, G. Machine learning for solar irradiance forecasting of photovoltaic system. Renew. Energy 2016, 90, 542–553.
  62. Mwende, R.; Waita, S.; Okeng’o, G. Real time photovoltaic power forecasting and modelling using machine learning techniques. E3S Web Conf. 2022, 354, 02004.
  63. Mahesh, B. Machine Learning Algorithms—A Review. Int. J. Sci. Res. 2020, 9, 381–386.
  64. Ray, S. A Quick Review of Machine Learning Algorithms. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 35–39.
  65. Josephine, P.K.; Prakash, V.S.; Divya, K.S. Supervised Learning Algorithms: A Comparison. Kristu Jayanti J. Comput. Sci. 2021, 1, 01–12.
  66. Jagadeesh, V.; Subbaiah, K.V.; Varanasi, J. Forecasting the probability of solar power output using logistic regression algorithm. J. Stat. Manag. Syst. 2020, 23, 1–16.
  67. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32.
  68. Hillebrand, E.; Medeiros, M. The Benefits of Bagging for Forecast Models of Realized Volatility. Econ. Rev. 2010, 29, 571–593.
  69. DVassallo, D.; Krishnamurthy, R.; Sherman, T.; Fernando, H.J.S. Analysis of Random Forest Modeling Strategies for Multi-Step Wind Speed Forecasting. Energies 2020, 13, 5488.
  70. Shi, K.; Qiao, Y.; Zhao, W.; Wang, Q.; Liu, M.; Lu, Z. An improved random forest model of short-term wind-power forecasting to enhance accuracy, efficiency, and robustness. Wind. Energy 2018, 21, 1383–1394.
  71. Natarajan, V.A.; Sandhya, K.N. Wind Power Forecasting Using Parallel Random Forest Algorithm. In Hybrid Artificial Intelligent Systems, Part II; Springer: Berlin/Heidelberg, Germany, 2015; p. 570.
  72. Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567.
  73. Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259.
  74. Zeng, J.; Qiao, W. Short-term solar power prediction using a support vector machine. Renew. Energy 2013, 52, 118–127.
  75. Meenal, R.; Selvakumar, A.I. Assessment of SVM, empirical and ANN based solar radiation prediction models with most influencing input parameters. Renew. Energy 2018, 121, 324–343.
  76. Dike, H.U.; Zhou, Y.; Deveerasetty, K.K.; Wu, Q. Unsupervised Learning Based on Artificial Neural Network: A Review. In Proceedings of the 2018 IEEE International Conference on Cyborg and Bionic Systems (CBS 2018), Shenzhen, China, 25–27 October 2019; pp. 322–327.
  77. Glielmo, A.; Husic, B.E.; Rodriguez, A.; Clementi, C.; Noé, F.; Laio, A. Unsupervised Learning Methods for Molecular Simulation Data. Chem. Rev. 2021, 121, 9722–9758.
  78. Karhunen, J.; Raiko, T.; Cho, K. Unsupervised deep learning: A short review. In Advances in Independent Component Analysis and Learning Machines; Elsevier: Amsterdam, The Netherlands, 2015; pp. 125–142.
  79. Usama, M.; Qadir, J.; Raza, A.; Arif, H.; Yau, K.-L.A.; Elkhatib, Y.; Hussain, A.; Al-Fuqaha, A. Unsupervised Machine Learning for Networking: Techniques, Applications and Research Challenges. IEEE Access 2019, 7, 65579–65615.
  80. Lai, J.-P.; Chang, Y.-M.; Chen, C.-H.; Pai, P.-F. A Survey of Machine Learning Models in Renewable Energy Predictions. Appl. Sci. 2020, 10, 5975.
  81. Varanasi, J.; Tripathi, M.M. K-means clustering based photo voltaic power forecasting using artificial neural network, particle swarm optimization and support vector regression. J. Inf. Optim. Sci. 2019, 40, 309–328.
  82. Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A Short-Term Wind Power Forecasting Approach with Adjustment of Numerical Weather Prediction Input by Data Mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291.
  83. Scolari, E.; Sossan, F.; Paolone, M. Irradiance prediction intervals for PV stochastic generation in microgrid applications. Sol. Energy 2016, 139, 116–129.
  84. Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38.
  85. Botvinick, M.; Ritter, S.; Wang, J.X.; Kurth-Nelson, Z.; Blundell, C.; Hassabis, D. Reinforcement Learning, Fast and Slow. Trends Cogn. Sci. 2019, 23, 408–422.
  86. Busoniu, L.; Ernst, D.; de Schutter, B.; Babuska, R. Approximate reinforcement learning: An overview. In Proceedings of the 2011 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning, Paris, France, 12–14 April 2011; pp. 1–8.
  87. Nian, R.; Liu, J.; Huang, B. A review on reinforcement learning: Introduction and applications in industrial process control. Comput. Chem. Eng. 2020, 139, 106886.
  88. Perera, A.; Kamalaruban, P. Applications of reinforcement learning in energy systems. Renew. Sustain. Energy Rev. 2020, 137, 110618.
  89. Shi, W.; Song, S.; Wu, C.; Chen, C.L.P. Multi Pseudo Q-Learning-Based Deterministic Policy Gradient for Tracking Control of Autonomous Underwater Vehicles. IEEE Trans. Neural Networks Learn. Syst. 2019, 30, 3534–3546.
  90. Grondman, I.; Busoniu, L.; Lopes, G.A.D.; Babuska, R. A Survey of Actor-Critic Reinforcement Learning: Standard and Natural Policy Gradients. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2012, 42, 1291–1307.
  91. Zhang, D.; Han, X.; Deng, C. Review on the research and practice of deep learning and reinforcement learning in smart grids. CSEE J. Power Energy Syst. 2018, 4, 362–370.
  92. Cao, D.; Hu, W.; Zhao, J.; Zhang, G.; Zhang, B.; Liu, Z.; Chen, Z.; Blaabjerg, F. Reinforcement Learning and Its Applications in Modern Power and Energy Systems: A Review. J. Mod. Power Syst. Clean Energy 2020, 8, 1029–1042.
  93. Sierra-García, J.E.; Santos, M. Exploring Reward Strategies for Wind Turbine Pitch Control by Reinforcement Learning. Appl. Sci. 2020, 10, 7462.
  94. Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799.
  95. Elsaraiti, M.; Merabet, A. Solar Power Forecasting Using Deep Learning Techniques. IEEE Access 2022, 10, 31692–31698.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
Video Production Service
Feedback