Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 1 by Yun Su and Version 2 by Sirius Huang.
Clothing as a tool connecting the human body and environment provides thermal and moisture comfort, and protective performance in cold, moderate, and extremely hot environments. The heat and moisture transfer properties of clothing materials are commonly evaluated using experimental study, mathematical modeling, and computer simulation.
- heat transfer
- clothing
- thermal comfort
- moisture transfer
1. Introduction
In most environmental conditions, the human body is capable of maintaining a constant core temperature. However, extreme environmental exposure makes it difficult for the human body to regulate its core temperature. This might induce hyperthermia or hypothermia in the human body [1]. Clothing that serves as a functional second skin can regulate the interaction effect between the human body and the external environment. The clothing can provide comfort, warmth retention, water resistance, thermal insulation, protection, etc., thus helping with personal thermal and moisture management [2].
A material with many interconnected pores can be treated as a porous medium [3]. Thus, clothing material is usually assumed as a porous media. However, the structure of the fabric becomes more complex due to the interweaving of the fibers and threads. Additionally, unlike conventional industrial materials, the majority of garment materials absorb moisture. Thus, understanding the mechanisms and behaviors associated with the coupled heat and moisture transfer in clothing materials is essential for personal thermal and moisture management. This helps to develop emerging clothing materials for improving human thermal and moisture comfort [4].
2. Heat Transfer in Clothing Materials
Heat transfer in the clothing materials was affected by multiple factors. Both conduction and convection require the presence of a medium for the transfer of thermal energy, but the radiative heat transfer is independent of any medium. Since the porosity of the commonly used fabrics is small enough, the convective heat transfer in the clothing is usually ignored [5][12]. The conductive heat transfer occurs in the fiber and the embedded air and moisture, while the radiative heat is just transported in the pore of the fabric. The conductive heat transfer is relatively simple and conformed to Fourier’s law while the radiant heat transfer in a porous medium is a complex process [6][13]. In the early stage, some conductive models were proposed to simulate the radiative heat transfer in clothing materials [7][8][14,15]. The conductive heat transfer in these models was treated as the main mode of heat transfer. An improved model that considered the radiative absorption and back-scattering property was developed by Schuster [9][16] for simulating the radiative heat transfer in fibrous materials [10][17]. At the end of the 20th century, Tong et al. [11][18] proposed a spectral two-flux model of the porous medium that simulated the thermal radiation with absorbing, emitting, and scattering, which can be expressed as,
where qλ+ and qλ− are the forward and backward radiant heat flux of micro-unit, respectively, σaλ and σsλ are the average absorptivity and scattering coefficient, ebλ is the emission of thermal radiation from blackbody, and bλ is the back-scattering factor.
There are two terms relating to the scattering of radiation in Equations (1) and (2). The first is the attenuation of energy by scattering for the second term on the right-hand side of Equations (1) and (2), while the final term on the right-hand side represents the augmentation of thermal radiation owing to the scattering. To simplify the solution method on the two-flux model, the effect of the radiative scattering portion in the fibrous materials was ignored. This was because the back- and forward-scattering of radiation could balance out in the one-dimensional heat transfer [12][19]. Therefore, the simple equations for the radiant heat transfer are given by,
Since then, the simple two-flux model was commonly utilized in modeling the radiative heat transfer in clothing materials under diverse environmental conditions [12][13][14][19,20,21]. Wan and Fan [15][22] employed the two-flux model to analyze the radiant heat transfer in fibrous assemblies incorporating reflective interlayers. Fu et al. [16][23] investigated the moisture influence on the absorption of thermal radiation under a low-level radiation exposure based on the two-flux model. Furthermore, the effects of self-emission and absorption of radiative heat transfer were investigated using the two-flux model to simulate thermal transfer in air gaps [17][18][24,25].
Another meaningful radiative transfer model was developed and validated experimentally by Torvi [19][26]. According to the structural model of fabric and the radiative transfer properties, it was found that the radiative heat transfer in the tested fabrics conformed to Beer’s law, as shown in Equation (5).
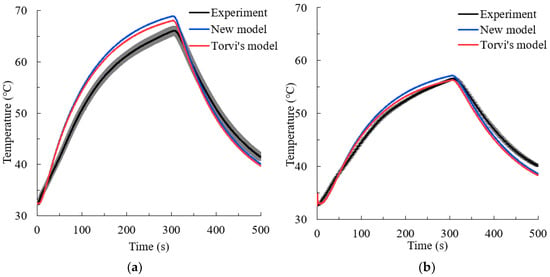
The thermal radiation through the fabrics exponentially decayed due to the fabric’s absorption and scattering [20][27]. The scattering and emission sources of radiative heat transfer were ignored in the model. It was suitable to the phenomenon that the decay of thermal radiation through the medium was far more than the emission of that, or the incident radiant heat unless the forward direction was rather less [6][13]. The model was popularly used to analyze the radiant heat transfer in thermal protective clothing [19][21][22][23][26,28,29,30]. In addition, an improved radiant heat transfer model (New model) was derived by considering the effect of the emission and compared with Torvi’s model [19][26], and the thermal protective performance test in low-level radiation (Experiment), as can be seen from Figure 14 [24][31]. The contrastive results demonstrated that the self-emission in the clothing material accelerated the rate of thermal energy transferred to the human skin during the thermal exposure and the cooling stage.
However, the aforementioned heat transfer models mostly considered one-dimensional heat transfer along the thickness direction of the clothing. The multi-dimensional heat transfer would occur if temperature differences existed on the surface of the clothing. In recent years, some CFD software was used to simulate the multi-dimensional heat transfer in clothing materials [25][26][27][28][29][32,33,34,35,36]. The irregular shape of a clothed body was accurately simulated to investigate the effects of clothing ventilation opening on heat transfer [30][31][37,38]. However, only conductive heat transfer was taken into account in the CFD models rather than the radiative heat transfer, and the porous property of the clothing materials was ignored, which created an obvious difference from the actual heat transfer [28][32][35,39].
3. Moisture Transfer in Clothing Materials
The moisture within the porous materials exists in three states: solid, liquid, or gas. The fiber and the absorbed water (bound water) become the solid phase of the fabric, while the gas phase is made up of a combination of entrapped air and water vapor [33][40]. Most moisture transfer models overlook the swelling or shrinkage of the fiber caused by moisture desorption or sorption since it is usually believed that the solid phase remains stationary. Therefore, the moisture transfer consists of the movement of water vapor due to the Fickian diffusion and Darcy’s flow, as well as the transport of liquid water depending on the external driving forces (such as pressure difference and gravity) and the internal driving forces (including capillary, intermolecular force, and permeation) [34][41], as given in Figure 25. Three states of water transform reciprocally owing to phase change and the fiber’s absorption/desorption.
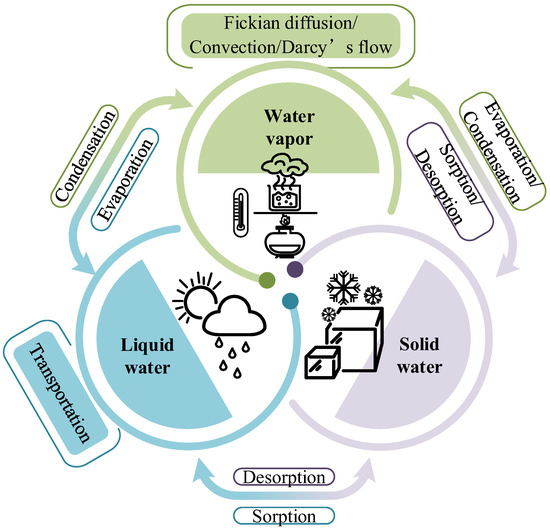
Figure 25.
Transportation and transformation for three types of water in clothing materials.
3.1. Water Vapor Transfer
Table 1 shows the typical models for water vapor transfer used in clothing materials. A mechanism for the transient diffusion of moisture in an assembly of textile fibers was first proposed and analyzed by Henry in 1939 [35][42]. The diffusion of water vapor in the fabric’s void space is driven by the component concentration gradient, required by the Fickian law [36][43]. Meantime, the water vapor diffuses through the fiber due to the molecular attraction on the fibrous surface. However, it is expected that the water vapor diffusion through the pores is more rapid than that through the fiber. Many researchers, such as Henry [37][44], Nordon and David [38][45], and Li and Holcombe [39][46], presented the continuous equations of water vapor in the inter-fiber void space and the fiber. However, the fiber can undergo swelling or shrinkage when the fiber absorbs or loses water, thus resulting in the variation of void space in the fiber and its geometry [40][9] (pp. 341–358). A thermal dynamic model was developed by Morton and Hearle [41][47] to evaluate the impacts of a fiber’s hygroscopicity, and physical and mechanical properties on the swelling effect, and. Gibson and Charmchi [42][48] proposed a mathematical model for the diffusion and convection of water vapor considering the influence of fiber’s swelling.
Table 1.
Typical water vapor transfer models used in the clothing.
| Representative Researchers | Factors Influencing the Water Vapor Transfer | |||||
|---|---|---|---|---|---|---|
| Molecular Diffusion | Darcy’s Flow | Sorption/Desorption | Phase Change | Air Resistance | Others | |
| Henry [37][44], Nordon and David [38][45], Li and Holcombe [39][46] | YES | NO | YES | NO | NO | NO |
| Morton and Hearle [41][47], Gibson and Charmchi [42][48] | YES | NO | YES | NO | NO | Swelling |
| Ogniewicz and Tien [43][49] | YES | NO | NO | YES | NO | NO |
| Li and Zhu [44][50] | YES | NO | YES | YES | NO | NO |
| Fan et al. [45][51] | YES | YES | NO | YES | NO | NO |
| Huang et al. [46][52] | YES | YES | YES | YES | YES | NO |
| Li et al. [47][53] | YES | YES | YES | YES | YES | NO |
| Luo et al. [48][54] | YES | YES | YES | YES | YES | Wind and velocity, body motion |
The phase change of moisture also influences water vapor transportation. The condensation process in the fabric would activate once the concentration of water vapor comes up to the saturated water vapor. Instead, the liquid water evaporates into water vapor. In previous studies, Ogniewicz and Tien [43][49] used an improved model to investigate the effect of evaporation/condensation on water vapor transfer. A more precise model of water vapor transfer considering the effects of absorption/desorption and evaporation/condensation was given by Li and Zhu [44][50]. In addition, the air in the fabric hinders the transfer of water vapor, since the gas phase is a mixture of air and water vapor [49][55]. The numerical models of the transfer of water vapor and air in the fabric were described by Huang et al. [46][52]. The effect of pressure gradient on the transfer of water vapor and air was also considered in the models. The pressure gradient can result in water vapor movement within the fibrous material, which was simulated according to Darcy’s law [45][51]. Li [47][53] and Luo et al. [48][54] derived a comprehensive moisture transfer model, which explained the effects of the concentration gradient, pressure gradient, air resistance, absorption/desorption, and evaporation/condensation on the transfer of water vapor.
3.2. Liquid Water Transport
Table 2 shows most factors influencing the liquid water transport in clothing materials. The early works of chemical engineers in drying processes were characterized by representing the fluid motion by diffusion equations, while some studies reported that the surface tension forces (capillary action) predominated the movement of liquid water in porous media [50][51][56,57]. To numerically simulate the liquid water transfer through the porous media, a threshold value of liquid water amount was given in some mathematical models for judging the beginning of liquid water flow [52][53][58,59]. Fan and Wen [54][60] derived a continuous equation on the liquid water diffusion in porous fibrous batting. The related dispersion coefficient was a function of the pore size and fiber surface treatment [54][60]. In accordance with Henry’s models, Li et al. [55][56][8,61] derived a special formula to describe the liquid water diffusivity in porous textiles. The condensation/evaporation, sorption/desorption, and liquid water transport by the capillary action were both considered in this equation.
However, the transportation of the liquid water was also dependent on gravity and convection, driven by the pressure gradient. It was supposed that the liquid water in a porous medium was a discontinuous phase. The impacts of the gravity and capillary action on the liquid water transport were analyzed in a moisture transfer model developed by Li and Zhu [57][62]. It was found that the gravity effects on the water transfer were dependent on the ratio of gravity to surface tension force in the porous textiles. Besides, Zhu et al. [58][63] presented a fractal model to investigate the physical model of liquid diffusion. It was assumed that the porous fibrous medium was a kind of fractal porous medium. Most factors affecting the liquid water flow were considered in this model (see Table 1). It was clear that porosity had a significant effect on the water vapor concentration in the void spaces and the liquid water flow.
However, there were few studies on multidimensional moisture transfer in past years. Until the early 21st century, Nashimura and Matsuo [59][64] presented a simple two-dimensional moisture transfer model of clothing materials that considered the water vapor transfer along the thickness and width direction based on Fickian second law and mass conservation law. However, the flow of liquid water and fiber sorption were ignored in the model. In addition, Luo and Xu [60][65] established a 3D geometric fiber model first and derived a new algorithm to simulate 2D transient moisture transport behavior. However, Darcy’s flow was not considered in this model. The liquid water transfer model was developed by Mao and Li [61][66] after an experimental method was used to investigate the multi-dimensional liquid moisture diffusion in clothing materials. However, the model precision and application should be further validated.
Table 2.
Models on liquid water transfer in clothing materials.
| Representative Researchers | Factors Influencing the Liquid Water Transfer | |||||
|---|---|---|---|---|---|---|
| Molecular Diffusion | Capillary Action | Darcy Flow | Sorption/Desorption | Phase Change | Gravity | |
| Fan and Wen [54][60] | YES | YES | NO | YES | YES | NO |
| Li and Zhu [56][61] | YES | YES | NO | YES | YES | NO |
| Wang et al. [62][67] | YES | YES | NO | YES | YES | NO |
| Li and Zhu [44][50] | YES | YES | NO | YES | YES | NO |
| Li et al. [47][53] | YES | YES | YES | YES | YES | NO |
| Huang et al. [46][52] | YES | YES | YES | YES | YES | NO |
| Wu and Fan [63][68] | YES | YES | NO | YES | YES | NO |
| Li and Zhu [57][62] | YES | YES | NO | YES | YES | YES |
| Zhu et al. [58][63] | YES | YES | YES | YES | YES | YES |
