You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 2 by Rita Xu and Version 1 by Enkhsaikhan Boldsaikhan.
Sustainable green products and services garner more attention from companies and enterprises that aim to succeed and grow in highly competitive markets by imposing less harms on the environment and ecosystems. Last-mile delivery from local distribution centers to customers plays an essential role in the retail business. Retail companies are leaning towards implementing green, efficient transportation methods, such as drones, in their last-mile delivery operations to conserve ecosystems.
- drone
- last-mile drone delivery
- routing
- cargo distribution optimization
1. Introduction
Transporting goods by sea, land/ground, and air requires sustainable logistics involving different vehicles to deliver parcels from one location to another. For instance, sea transportation uses ships and boats, land/ground transportation uses railroad trains, trucks, cars, and bikes, and air transportation uses airplanes and drones. Last-mile delivery operations mostly use trucks. In fact, trucks are the most employed tool in urban logistics. However, utilizing trucks in last-mile delivery has limitations, such as being unable to provide deliveries to some rural regions that are hard to reach by truck, consuming gasoline that leads to air pollution, being unable to deliver parcels in a timely manner due to traffic jams, etc. A potential eco-friendly vehicle in last-mile delivery is a bicycle. Retail companies such as DoorDash [1,2][1][2] and UberEats [3,4][3][4] use bicycles to deliver parcels to urban customers. However, bicycle delivery has drawbacks, such as exposing the bicycle riders to traffic hazards, requiring longer delivery times, and having limited cargo capacities. Generally, bicycle delivery is good for neighborhoods, but it may not be efficient in urban areas [5].
The invention of the drone technology [6] enabled the use of drones in last-mile delivery to complement the existing transportation methods. Abraham Karem [6] is the inventor of drone technology. He was passionate about aircraft and started building prototype aircraft when he was a teenager. He immigrated to the United States of America in the 1970s and later founded a company, Leading Systems Inc., in his home garage [6]. He started manufacturing his first drone named Albatross, followed by the more advanced Amber [7], which became the predecessor of the famed Predator drone [8] that brought him the “Drone father” designation. The propulsion system of a drone consists of motors, electronic speed controllers, and propellers, which allow the drone to fly and maneuver in the air. Hassanalian and Abdelkefi [9] categorized the drone types in terms of their weights, characteristics, and capabilities. Based on the propulsion system and the structural design, there are four major types of drones; multi-rotor drones [10], fixed-wing drones [11], single-rotor helicopter [12[12][13],13], and fixed-wing hybrid VTOL (Vertical Take-Off and Landing) drones [14]. Drones [15,16][15][16] benefit global industries by increasing work efficiency and productivity, decreasing workload and production costs, improving accuracy and repeatability, refining service and customer relations, and resolving security issues on a vast scale.
The Internet and digital transformation allowed more retail companies to use electronic commerce, or e-commerce [17]. E-Commerce has been the primary method of shopping, especially during the 2019–2021 pandemic, when more than half of the world population had to stay at home [18]. This is the primary reason global parcel volume increased from 87 billion in 2018 to more than 126 billion in 2020 and is predicted to reach 200 billion by 2025 [19]. In 2019, UPS, FedEx, and Amazon only delivered about 11.2 billion packages in the United States of America (USA).
Trucks are the primary transportation method for last-mile delivery. Fossil-fuel trucks cause noise and air pollution, traffic jams, cluttered parking spots, traffic accidents, higher delivery costs, and other unforeseen ground vehicle issues. Delivery trucks [20] are about 4% of vehicles on the USA roads; they cause about 50% of the nitrogen oxide emissions, 60% of the fine particulates, and 7% of all greenhouse gas emissions in the USA. Hence, many retail companies, such as Amazon, Alphabet Wing, Walmart, UPS, etc., lean toward using the drone technology as a sustainable transportation method as it offers eco-friendly, faster delivery with lower operating costs and less human involvements [21,22,23,24,25,26][21][22][23][24][25][26]. Other companies, such as Mercedes-Benz, started collaborating with the drone manufacturer Matternet to implement the on-demand delivery of e-commerce products using electric vans and drones [27]. Besides delivering standard parcels, drones are also used in food delivery [1,4,28,29,30,31,32,33][1][4][28][29][30][31][32][33], vaccine delivery [31[31][34][35][36][37],34,35,36,37], and the delivery of other lifesaving supplies in disaster relief operations [37]. However, utilizing drones in last-mile delivery has numerous challenges, such as reducing delivery costs, increasing energy efficiency, lowering environmental harms, tracking parcel deliveries, preventing sporadic delays in deliveries, staying on track with advanced technologies, etc.
2. Routing
2.1. Advancements
Routing is an essential challenge to address as it aims to find optimum delivery routes that make last-mile drone delivery economically and operationally feasible. Trucks are necessary to carry drones and supplies as well as parcels in last-mile drone delivery. Therefore, last-mile drone delivery routing should consider routes for both drones and trucks. Depending on drone-and-truck arrangements, last-mile drone delivery routing may involve one drone and one truck, multiple drones and one truck, or multiple drones and multiple trucks. Long before utilizing drones in last-mile delivery, Dantzig and Ramser [91][38] introduced the vehicle routing problem (VRP) in 1959 to find the optimal set of routes for a fleet of vehicles to deliver to a given group of customers. They were concerned with the optimal route of a fleet of gasoline delivery trucks between the storage of petroleum products to stations. The goal of the VRP is to minimize the total route a fleet should travel. Clarke and Write [92][39] enhanced the VRP algorithm proposed by Dantzig and Ramser [91][38] by using a compelling greedy perspective called the “savings algorithm”. A novel solution that extends the classic Clarke-and-Wright algorithm [92][39] is a mathematical model developed by Karak and Abdelghany [39][40] to solve the Hybrid Vehicle-Drone Routing Problem (HVDRP). They set three experiments to examine the capability of their proposed model to solve different vehicle-drone routing problems. They developed three heuristics, the hybrid Clarke and Wright heuristic (HCWH), the vehicle-driven heuristic (VDH), and the drone-driven heuristic (DDH), for solving HVDRP. Murray and Chu [38][41] extended the HVDRP model [39][40] and introduced the Flying Sidekick Traveling Salesman Problem (FSTSP) in 2015 to find optimal routing and scheduling for multiple drones and a truck. In operations research, the makespan is the time taken between the start and the end of work. If the makespan of the truck exceeds that of the drone, minimal improvement may be possible, given that solutions are initialized to assign all drone-eligible customers to drones. Therefore, the ongoing strategy focuses on the drone to monitor whether its makespan surpasses the truck. If so, reducing the drone makespan is considered by shifting customers to the delivery truck. Gonzalez-R et al. [93][42] introduced a mathematical model, an iterated greedy heuristic method, using a simulated annealing (SA) algorithm to optimize the truck-and-drone delivery routes. The model works with one truck and one drone. During the package delivery, the drone will come back to the truck to swap/recharge the battery when needed as the truck is a battery swap station for the drone as well. This means that the drone needs to calculate the remaining battery life, and, if the drone needs new batteries, it will join the truck at the next truck stop where the truck delivers a package. If the truck reaches the stop sooner than the drone, it will wait for the drone to join and vice versa. They also considered that drones could have multi-drop routes, which will help drones deliver to multiple customers by eliminating unnecessary travel to the truck. There is no limitation on the battery swap operation for drones, and each time drone will leave the truck with full batteries and/or a newly assigned delivery task. Es Yurek and Ozmutlu [94][43] work on FSTSP to reduce the completion time of last-mile delivery. They proposed an iterative algorithm based on the decomposition approach. In the first step, they find the truck route and determine which customer is eligible for drone delivery based on weight, travel distance, and accessibility. In the second step, a mixed-integer linear programming model is used to optimize the drone route by fixing the routing and the assignment decisions made in the first stage. Lemardelé et al. [95][44] investigated two delivery methods—FSTSP and a method with ground autonomous delivery devices (GADDs). They suggested that the cost of drones with a truck is minimal in smaller areas with less dense locations. However, in dense areas, it is more justifiable to use the GADD method to reduce the cost of the operation. Salama and Srinivas [78][45] studied last-mile delivery with multiple drones and a single truck, which is a multiple-drone VRP. They proposed to divide the customer sites into clusters, establish a dispatch point in each group for the truck to launch the delivery drones, and optimize the truck route for the dispatch points. The truck stops at each dispatch point, and drones start their deliveries to customers; meanwhile, the truck does deliveries to its assigned customers. They used an unsupervised machine learning heuristic algorithm to minimize the total delivery cost and time. Kitjacharoenchai et al. [44][46] extended FSTSP [38][41] to include multiple drones and multiple trucks in the model that is referred to as the Two Echelon Vehicle Routing Problem with Drones (2EVRPD). The study aims to find optimized routes for drones and trucks while minimizing delivery time. Moshref-Javadi et al. [42,96][47][48] presented an extension of HVDRP [39][40] to optimize last-mile delivery routes, where both drones and trucks work simultaneously. A truck acts as a mobile depot, while drones deliver packages to customers, one customer per dispatch due to its weight limit. Trucks can also deliver parcels to multiple customers. This synchronized system is used to minimize customer waiting time. Bakir and Tiniç [70][49] introduced another extension of HVDRP [39][40] where the drones are allowed to be flexible, which means drones can connect to all the trucks in the system. They called it Vehicle Routing Problem with Flexible Drone (VRPFD) and tried to find a set of routes for a fleet of drones and trucks working simultaneously in the system. They also allowed trucks to visit an exact location more than one time. They also suggested that flexible drone utilization reduced the makespan by up to 12.12%, with an average of 5.39%. Shavarani et al. [79][50] stated that using a drone fleet in last-mile delivery would reduce the waiting time and the transportation cost. They developed a multi-objective mathematical model to find optimum locations for depots in the vicinity of customer locations. The customers closest to the depot have higher priorities for receiving the delivery services. Thus, the overall travel distance can be reduced, followed by reduced costs. As last-mile delivery in urban areas directly influences customers, retail companies regard it as a powerful tool for attracting more consumers. Drones with intelligent routing capabilities would benefit last-mile delivery by offering eco-friendly, lean, reliable, fast, and sustainable delivery services. In particular, the implementation of flying sidekick drones and trucks in last-mile delivery, as illustrated in Figure 1, would help reduce the overall operation cost, fuel consumption, and environmental harms.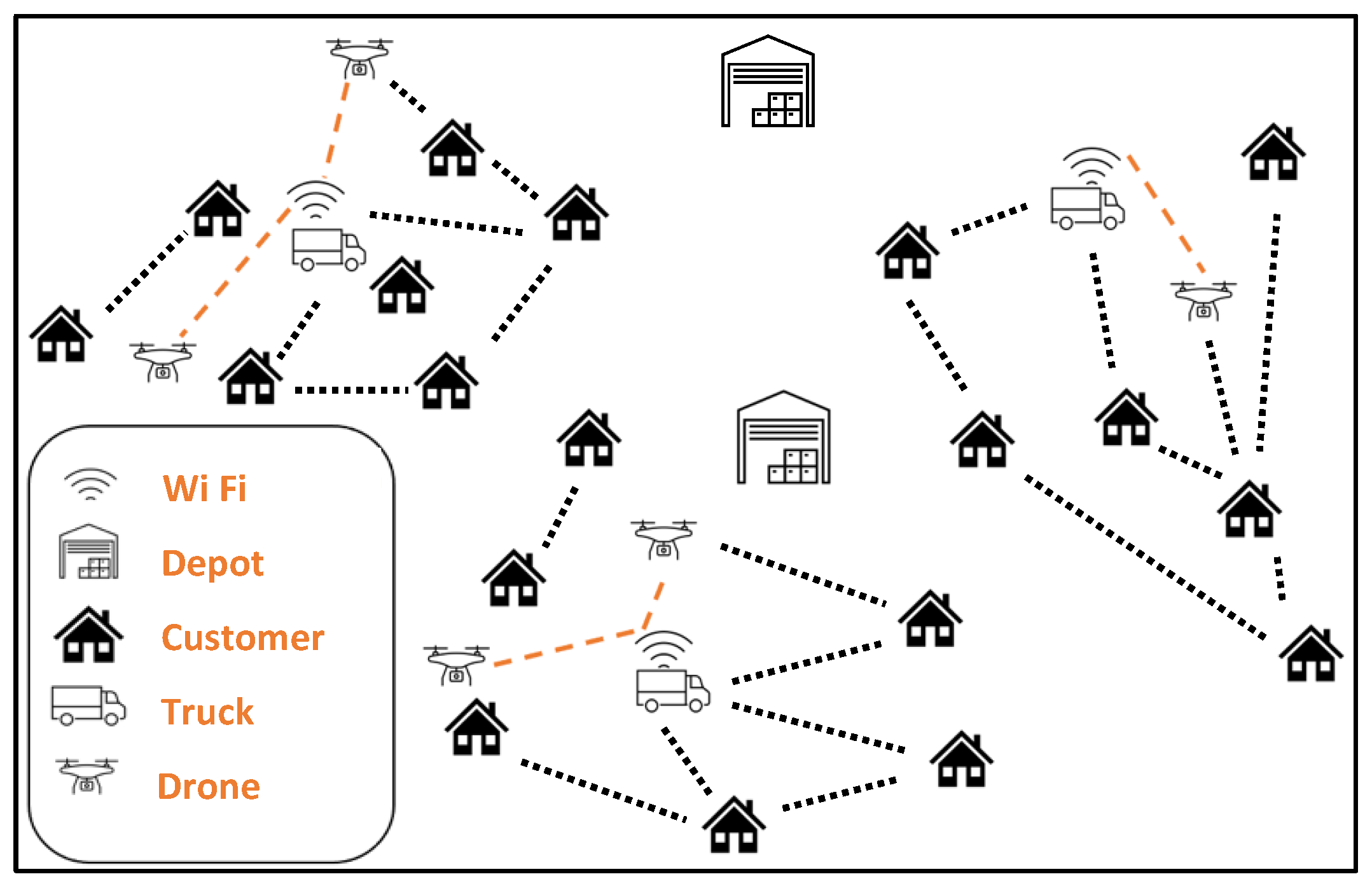
Figure 1. This figure illustrates flying sidekick drones and trucks in last-mile delivery.
2.2. Opportunities
Based on FSTSP [38][41], Murray and Raj [40][51] documented an exciting study on multiple Flying Sidekick Traveling Salesman Problem (mFSTSP). They explained that, because of the complex nature of the routing problem, they could not rely on mixed-integer linear programming (MILP). Perhaps, a practical solution can be achieved by using a heuristic approach. Murray and Raj, as well as other researchers [38,40,42[41][46][47][49][51],44,70], mostly focused on optimizing the delivery routes to minimize the total delivery time of the truck-and-drone fleet. There are some research opportunities to optimize the delivery routes with respect to other targets, such as energy efficiency, customer satisfaction, etc. Sacramento et al. [43][52] formulated a mathematical model similar to FSTSP [38][41] with additional constraints. They used time limit control for the capacitated multiple-truck cases to minimize the distribution cost. They noticed that using small aircraft, such as drones, has obvious advantages over the truck-only distribution of goods. However, their model only looked at fuel costs of the distribution and no other factors, such as cargo capacities, maintenance, driver salaries, other operational expenses, etc. As vehicle routing is an open-ended problem, researchers are still exploring new heuristic/metaheuristic algorithms or new linear/nonlinear optimization techniques to advance the last-mile drone delivery operation. Moreover, drones still experience some logistic challenges when delivering items to customer places. They can deliver items to accessible places, such as the front door or the back yard of a house. However, such delivery approaches may pose security concerns as the delivered items may be left unattended. In addition, drones cannot deliver packages to mailboxes or apartment buildings. Therefore, last-mile drone delivery needs more research and development to find secure, diverse ways to deliver items to diverse customer places.3. Cargo Distribution Optimization
3.1. Advancements
Cargo distribution optimization is a critical challenge to address as it offers proper distribution of parcels among delivery trucks, drones, bicycles, and robots for last-mile delivery. Delivery vehicles have different cargo capacity limits, safety ratings, reliability levels, and energy consumption. On the other side, parcels have different sizes, weights, destinations, urgency levels, priorities, safe-handling requirements, and costs [45,46,47,48][53][54][55][56]. Cargo distribution optimization may involve combinatorial optimization (i.e., Knapsack Problem (KP) [49[57][58][59][60],50,51,52], Bin Packing Problem (BPP) [47,51,53,54][55][59][61][62]), and cargo distribution scheduling [55,56,57][63][64][65]. Vehicle routing and cargo distribution among delivery vehicles are major optimization problems in supply-chain management [45][53]. Naumov and Pawluś [51][59] reviewed last-mile delivery in urban zones with restrictions on motorized vehicles and the use of cargo bicycles in those zones. They focused on efficient packing, routing, and speed limitations that depend on the cargo load. The Traveling Salesman Problem (TSP) and the Knapsack Problem (KP) were involved in minimizing the distance and maximizing the specific bicycle cargo. This study considered a number of homogenous bicycles and a number of packages with different weights and sizes. KP deals with assigning packages to bicycles, and TSP deals with optimizing the route of each bicycle. They used three algorithms to optimize packaging and routing problems. The first algorithm is the Bin-Pack-3D method that consists of two steps. The first step finds optimum package-cargo combinations, and the second step optimizes the bicycle delivery routes. The second algorithm is the Multiple Traveling Salesman Problem (MTSP), which finds every possible path for all bicycles and selects the most feasible route for each bicycle. The third algorithm, the Capacitated Traveling Salesman Problem (CTSP), finds service stations with delivery bicycles, whereas each bicycle has a limited cargo capacity. They compared the three algorithms and found that the three algorithms produced almost identical results in terms of the overall delivery time and distance. Sorbelli et al. [56][64] introduced the Multiple-Drone-Delivery Scheduling Problem (MDSP) that involves drones assisted by trucks. This study aimed to search for the optimal scheduling of drones to use their maximum battery life by ensuring that the battery power does not deplete during delivery. The study involved KP in managing a set of delivery tasks to maximize profit by considering the drone energy consumption and the cargo capacity limits of drones. Correspondingly, Zhang [49][57] examined the practicality of using automated delivery robots to deliver packages with different weights and sizes. The presented approach [49][57] consists of three steps. The first step is to use the Generalized Linear Model (GLM) to fit the total volume of packages for distribution cycles. The second step is to solve a routing problem for delivery robots by using a three-dimensional KP concept. The third step uses a mixed-integer linear programming model to optimize the total distance and the energy required by each delivery robot. The proposed approach demonstrated that using delivery robots is more practical and efficient. Parcel priority is another parameter to consider in cargo distribution and scheduling [97][66]. Deplano et al. [52][60] proposed a mixed-integer linear programming model for the multiple heterogeneous KP with realistic container loading constraints and the priority of bins/parcels. Yildiz [50][58] compared exact KP methods with approximate KP methods. Exact KP methods are time-consuming because of the NP-hard (non-deterministic polynomial-time hard) nature of the problem. Therefore, the study focused on a deep reinforcement learning model as an approximate KP method. It involved a neural net with fully connected layers. The experimental results demonstrated that the proposed approximate KP method was about 40 times faster than the exact KP methods. Capacity in logistics is the amount of physical space, assets, and employees available to carry, store, and deliver packages. Warehouses, trucks, drones, and employees are examples of last-mile drone delivery capacity elements. Predicting the next-day package volume is an important capacity planning problem [54][62]. Fadda et al. [53][61] introduced a machine-learning model to predict the next-day distribution volume and the number of vehicles needed to distribute parcels using historical data. They utilized machine learning methods to predict demand based on historical data. They clustered the customer locations and assigned a fleet to each cluster based on the distribution volume of each cluster by Tactical Capacity Planning (TCP). Implementing cargo distribution optimization concepts in last-mile delivery helps retail companies gain more profits as it aims to optimize the cargo distribution process as well as scheduling/planning. Although researchers proposed numerous brute-force methods as well as heuristic methods for cargo distribution optimization and scheduling/planning, there is always room for advancements to make the cargo distribution operation more eco-friendly, more efficient, and more profitable.3.2. Opportunities
Delivery vehicles have different cargo capacity limits, safety ratings, reliability levels, eco ratings, and energy consumption. On the other side, parcels have different sizes, weights, destinations, urgency levels, priorities, safe-handling requirements, and costs [45,46,47,48][53][54][55][56]. Hence, assigning parcels to delivery vehicles requires proper cargo distribution to optimize the target performances of last-mile delivery with respect to budget limits, time constraints, or any other restrictions on the delivery operation. In addition, forecasting the future parcel volumes is a challenging problem to solve for cargo distribution scheduling as it involves various levels of uncertainty. Last-mile delivery now tends to use various delivery vehicles, such as trucks, drones, bicycles, mobile robots, etc. Therefore, cargo distribution optimization with heterogeneous delivery vehicles needs more accurate linear/nonlinear mathematical models for optimization and further investigation, so that different types of delivery vehicles may effectively complement each other in certain situations. Furthermore, the aspect of unusual parcel shapes is underestimated in cargo distribution optimization. Handling parcels with unusual shapes in a safe, secure, timely manner adds new complexities to cargo distribution and scheduling.References
- Rieck, K.R. Which Company Is Winning the Food Delivery War. Available online: https://secondmeasure.com/datapoints/food-delivery-services-grubhub-uber-eats-doordash-postmates/ (accessed on 20 December 2022).
- Zhang, Y. Qualitative Analysis of DoorDash. In Proceedings of the 2021 3rd International Conference on Economic Management and Cultural Industry (ICEMCI 2021), Guangzhou, China, 22–24 October 2021; pp. 65–68.
- Barykin, S.Y.; Kapustina, I.V.; Kalinina, O.V.; Dubolazov, V.A.; Esquivel, C.A.N.; Alyarovna, N.E.; Sharapaev, P. The Sharing Economy and Digital Logistics in Retail Chains: Opportunities and Threats. Acad. Strateg. Manag. J. 2021, 20, 1–14.
- Stonehem, B. UberEats Food Delivery: Learning the Basics; First Rank Publishing: Mountain View, CA, USA, 2016; Volume 1.
- Zhang, L.; Matteis, T.; Thaller, C.; Liedtke, G. Simulation-based Assessment of Cargo Bicycle and Pick-up Point in Urban Parcel Delivery. Procedia Comput. Sci. 2018, 130, 18–25.
- Seharwat, V. Historical Introduction and Technology Used in Drones. In Drones and the Law; Emerald Publishing Limited: Bingley, UK, 2020; pp. 1–21.
- Economist, T. The Dronefather. Available online: https://www.economist.com/technology-quarterly/2012/12/01/the-dronefather (accessed on 31 December 2022).
- Whittle, R. Predator: The Secret Origins of the Drone Revolution; Henry Holt and Company, LLC.: New York, NY, USA, 2014.
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131.
- Yang, H.; Lee, Y.; Jeon, S.-Y.; Lee, D. Multi-rotor drone tutorial: Systems, mechanics, control and state estimation. Intell. Serv. Robot. 2017, 10, 79–93.
- Elijah, T.; Jamisola, R.S.; Tjiparuro, Z.; Namoshe, M. A review on control and maneuvering of cooperative fixed-wing drones. Int. J. Dyn. Control. 2021, 9, 1332–1349.
- Zhao, P.; Quan, Q.; Chen, S.; Tang, D.; Deng, Z. Experimental investigation on hover performance of a single-rotor system for Mars helicopter. Aerosp. Sci. Technol. 2019, 86, 582–591.
- Bautista-Medina, J.A.; Lozano, R.; Osorio-Cordero, A. Modeling and Control of a Single Rotor Composed of Two Fixed Wing Airplanes. Drones 2021, 5, 92.
- Jo, D.; Kwon, Y. Analysis of VTOL UAV propellant technology. J. Comput. Commun. 2017, 5, 76–82.
- Kellermann, R.; Biehle, T.; Fischer, L. Drones for parcel and passenger transportation: A literature review. Transp. Res. Interdiscip. Perspect. 2020, 4, 100088.
- Gonzalez-Aguilera, D.; Rodriguez-Gonzalvez, P. Drones—An Open Access Journal. Drones 2017, 1, 1.
- Schneider, G. Electronic Commerce; Cengage Learning: Boston, MA, USA, 2016.
- Bhatti, A.; Akram, H.; Basit, H.M.; Khan, A.U.; Raza, S.M.; Naqvi, M.B. E-commerce trends during COVID-19 Pandemic. Int. J. Future Gener. Commun. Netw. 2020, 13, 1449–1452.
- Pitney_Bowes_Inc. Parcel Shipping Exceeds 131bn in Volume Globally, and It’s Likely to More than Double by 2026. Available online: https://www.pitneybowes.com/us/shipping-index.html (accessed on 20 December 2022).
- O’Connor, T. 100% Zero-Emissions Trucks. How Close Are We? Environ. Def. Fund Sept. 2020, 16, 2020.
- Boysen, N.; Fedtke, S.; Schwerdfeger, S. Last-mile delivery concepts: A survey from an operational research perspective. OR Spectr. 2021, 43, 1–58.
- Brunner, G.; Szebedy, B.; Tanner, S.; Wattenhofer, R. The urban last mile problem: Autonomous drone delivery to your balcony. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (Icuas), Atlanta, GA, USA, 11–14 June 2019; pp. 1005–1012.
- Frachtenberg, E. Practical Drone Delivery. Computer 2019, 52, 53–57.
- Sawadsitang, S.; Niyato, D.; Tan, P.S.; Wang, P. Supplier Cooperation in Drone Delivery. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5.
- Sawadsitang, S.; Niyato, D.; Tan, P.S.; Wang, P.; Nutanong, S. Shipper Cooperation in Stochastic Drone Delivery: A Dynamic Bayesian Game Approach. IEEE Trans. Veh. Technol. 2021, 70, 7437–7452.
- Nemer, I.A.; Sheltami, T.R.; Mahmoud, A.S. A game theoretic approach of deployment a multiple UAVs for optimal coverage. Transp. Res. Part A Policy Pract. 2020, 140, 215–230.
- Mercedes-Benz Group Media. Vans & Drones in Zurich: Mercedes-Benz Vans, Matternet and Siroop Start Pilot Project for On-Demand Delivery of E-Commerce Goods. Available online: https://group-media.mercedes-benz.com/marsMediaSite/en/instance/ko/Vans--Drones-in-Zurich-Mercedes-Benz-Vans-Matternet-and-siroop-start-pilot-project-for-on-demand-delivery-of-e-commerce-goods.xhtml?oid=29659139 (accessed on 12 December 2022).
- Waris, I.; Ali, R.; Nayyar, A.; Baz, M.; Liu, R.; Hameed, I. An Empirical Evaluation of Customers’ Adoption of Drone Food Delivery Services: An Extended Technology Acceptance Model. Sustainability 2022, 14, 2922.
- Jasim, N.I.; Kasim, H.; Mahmoud, M.A. Towards the Development of Smart and Sustainable Transportation System for Foodservice Industry: Modelling Factors Influencing Customer’s Intention to Adopt Drone Food Delivery (DFD) Services. Sustainability 2022, 14, 2852.
- Patel, H. Designing Autonomous Drone for Food Delivery in Gazebo/Ros Based Environments; Technical Report; Binghamton University: Binghamton, NY, USA, 2022; Available online: https://scholar.smu.edu/engineering_compsci_research/6 (accessed on 12 December 2022).
- Mohsan, S.A.H.; Zahra, Q.u.A.; Khan, M.A.; Alsharif, M.H.; Elhaty, I.A.; Jahid, A. Role of Drone Technology Helping in Alleviating the COVID-19 Pandemic. Micromachines 2022, 13, 1593.
- Hwang, J.; Kim, D.; Kim, J.J. How to Form Behavioral Intentions in the Field of Drone Food Delivery Services: The Moderating Role of the COVID-19 Outbreak. Int. J. Environ. Res. Public Health 2020, 17, 9117.
- Mathew, A.O.; Jha, A.N.; Lingappa, A.K.; Sinha, P. Attitude towards Drone Food Delivery Services—Role of Innovativeness, Perceived Risk, and Green Image. J. Open Innov. Technol. Mark. Complex. 2021, 7, 144.
- Dickson, I. Flying Pharmacy: Why Medical Drones will Take off in 2022. Available online: https://www.here.com/learn/blog/medical-drones (accessed on 14 March 2022).
- Sham, R.; Siau, C.S.; Tan, S.; Kiu, D.C.; Sabhi, H.; Thew, H.Z.; Selvachandran, G.; Quek, S.G.; Ahmad, N.; Ramli, M.H.M. Drone Usage for Medicine and Vaccine Delivery during the COVID-19 Pandemic: Attitude of Health Care Workers in Rural Medical Centres. Drones 2022, 6, 109.
- Haidari, L.A.; Brown, S.T.; Ferguson, M.; Bancroft, E.; Spiker, M.; Wilcox, A.; Ambikapathi, R.; Sampath, V.; Connor, D.L.; Lee, B.Y. The economic and operational value of using drones to transport vaccines. Vaccine 2016, 34, 4062–4067.
- Rabta, B.; Wankmüller, C.; Reiner, G. A drone fleet model for last-mile distribution in disaster relief operations. Int. J. Disaster Risk Reduct. 2018, 28, 107–112.
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91.
- Clarke, G.; Wright, J.W. Scheduling of Vehicles from a Central Depot to a Number of Delivery Points. Oper. Res. 1964, 12, 568–581.
- Karak, A.; Abdelghany, K. The hybrid vehicle-drone routing problem for pick-up and delivery services. Transp. Res. Part C Emerg. Technol. 2019, 102, 427–449.
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109.
- Gonzalez-R, P.L.; Canca, D.; Andrade-Pineda, J.L.; Calle, M.; Leon-Blanco, J.M. Truck-drone team logistics: A heuristic approach to multi-drop route planning. Transp. Res. Part C Emerg. Technol. 2020, 114, 657–680.
- Es Yurek, E.; Ozmutlu, H.C. A decomposition-based iterative optimization algorithm for traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2018, 91, 249–262.
- Lemardelé, C.; Estrada, M.; Pagès, L.; Bachofner, M. Potentialities of drones and ground autonomous delivery devices for last-mile logistics. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102325.
- Salama, M.; Srinivas, S. Joint optimization of customer location clustering and drone-based routing for last-mile deliveries. Transp. Res. Part C Emerg. Technol. 2020, 114, 620–642.
- Kitjacharoenchai, P.; Min, B.-C.; Lee, S. Two echelon vehicle routing problem with drones in last mile delivery. Int. J. Prod. Econ. 2020, 225, 107598.
- Moshref-Javadi, M.; Hemmati, A.; Winkenbach, M. A truck and drones model for last-mile delivery: A mathematical model and heuristic approach. Appl. Math. Model. 2020, 80, 290–318.
- Moshref-Javadi, M.; Lee, S.; Winkenbach, M. Design and evaluation of a multi-trip delivery model with truck and drones. Transp. Res. Part E Logist. Transp. Rev. 2020, 136, 101887.
- Bakir, I.; Tiniç, G.Ö. Optimizing Drone-Assisted Last-Mile Deliveries: The Vehicle Routing Problem with Flexible Drones. Optim. Online 2020, 1–28.
- Shavarani, S.M.; Golabi, M.; Izbirak, G. A capacitated biobjective location problem with uniformly distributed demands in the UAV-supported delivery operation. Int. Trans. Oper. Res. 2021, 28, 3220–3243.
- Murray, C.C.; Raj, R. The multiple flying sidekicks traveling salesman problem: Parcel delivery with multiple drones. Transp. Res. Part C Emerg. Technol. 2020, 110, 368–398.
- Sacramento, D.; Pisinger, D.; Ropke, S. An adaptive large neighborhood search metaheuristic for the vehicle routing problem with drones. Transp. Res. Part C Emerg. Technol. 2019, 102, 289–315.
- Marmolejo-Saucedo, J.A. Digital twin framework for large-scale optimization problems in supply chains: A case of packing problem. Mob. Netw. Appl. 2022, 27, 2198–2214.
- Hifi, M.; M’hallah, R. A literature review on circle and sphere packing problems: Models and methodologies. Adv. Oper. Res. 2009, 2009, 150624.
- Munien, C.; Ezugwu, A.E. Metaheuristic algorithms for one-dimensional bin-packing problems: A survey of recent advances and applications. J. Intell. Syst. 2021, 30, 636–663.
- Chauhan, D.; Unnikrishnan, A.; Figliozzi, M. Maximum coverage capacitated facility location problem with range constrained drones. Transp. Res. Part C Emerg. Technol. 2019, 99, 1–18.
- Zhang, C. Feasibility Analysis and Efficient Routing for a Partially Automated Delivery System within Chalmers Campus; University of Gothenburg: Gothenburg, Sweden, 2021.
- Yildiz, B. Reinforcement learning using fully connected, attention, and transformer models in knapsack problem solving. Concurr. Comput. Pract. Exp. 2021, 34, e6509.
- Naumov, V.; Pawluś, M. Identifying the Optimal Packing and Routing to Improve Last-Mile Delivery Using Cargo Bicycles. Energies 2021, 14, 4132.
- Deplano, I.; Lersteau, C.; Nguyen, T.T. A mixed-integer linear model for the multiple heterogeneous knapsack problem with realistic container loading constraints and bins’ priority. Int. Trans. Oper. Res. 2021, 28, 3244–3275.
- Fadda, E.; Fedorov, S.; Perboli, G.; Dario Cardenas Barbosa, I. Mixing machine learning and optimization for the tactical capacity planning in last-mile delivery. In Proceedings of the 2021 IEEE 45th Annual Computers, Software, and Applications Conference (COMPSAC), Madrid, Spain, 12–16 July 2021; pp. 1291–1296.
- Crainic, T.G.; Gobbato, L.; Perboli, G.; Rei, W. Logistics capacity planning: A stochastic bin packing formulation and a progressive hedging meta-heuristic. Eur. J. Oper. Res. 2016, 253, 404–417.
- Asadi, A.; Nurre Pinkley, S. A stochastic scheduling, allocation, and inventory replenishment problem for battery swap stations. Transp. Res. Part E Logist. Transp. Rev. 2021, 146, 102212.
- Betti Sorbelli, F.; Corò, F.; Das, S.; Palazzetti, L.; Pinotti, C. Greedy Algorithms for Scheduling Package Delivery with Multiple Drones. In Proceedings of the ICDCN 2022: 23rd International Conference on Distributed Computing and Networking, Delhi, India, 30 September 2021.
- Torabbeigi, M.; Lim, G.J.; Kim, S.J. Drone delivery scheduling optimization considering payload-induced battery consumption rates. J. Intell. Robot. Syst. 2020, 97, 471–487.
- Perboli, G.; Gobbato, L.; Perfetti, F. Packing Problems in Transportation and Supply Chain: New Problems and Trends. Procedia -Soc. Behav. Sci. 2014, 111, 672–681.
More
