Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Sirius Huang and Version 1 by Miha Moškon.
Genome-scale metabolic models (GEMs) aim to systematically encode knowledge of the metabolism of an organism. GEMs are composed of different layers of information and are constructed with a combination of automated approaches and manual curation based on the available literature and experimental data. These models not only encode existing knowledge about an organism, but can also generate new knowledge through various analytical methods. The latter are mostly focused on the assessment of reaction fluxes through the metabolic network in different conditions.
- context-specific genome scale metabolic modelling
- constraint-based modelling
- omics data integration
- metabolism
- genome scale metabolic modelling
- systems biology
- systems medicine
1. Introduction
Genome-scale metabolic models (GEMs) have found numerous applications in different domains, ranging from biotechnology to systems medicine [1]. One of their main benefits is that they can provide genotype-to-phenotype projections, such as growth rate and nutrient uptake predictions, and predictions of metabolic flux values. The latter can be used to assess metabolic reaction activities in different contexts [2,3][2][3]. A GEM describes a metabolic network with a stoichiometric matrix [4] and each reaction is constrained by its minimal and maximal flux bounds. Moreover, a GEM usually encodes the information on gene–protein reaction (GPR) associations, which can be applied in the adaptation of a GEM to a specific context described with high-throughput data, such as transcriptomics or proteomics data. Such integration can be performed with the application of context-specific model reconstruction algorithms, which are used to adapt the flux bounds of a reference model to a given context described with (at least one) high-throughput dataset. This allows one to at least partially automatise the reconstruction of tissue-specific, cell type-specific, disease-specific, or even personalised GEMs. Further investigation of context-specific GEMs includes comparative analyses between different conditions (e.g., analysis of metabolic reprogramming in cancer cells [5]), and identification of biomarkers and therapeutic targets in different diseases or disorders [6].
2. Genome-Scale Metabolic Modelling
Genome-scale metabolic models (GEMs) aim to systematically encode our knowledge of the metabolism of an organism. Reference GEMs describing generic models of a cell are constructed with a combination of automated approaches and manual curation. Such reconstructions are based on genome annotation data and a myriad of additional data sources, including biochemical databases, organism-specific databases, experimental data, and literature data [7]. GEM reconstruction, its refinement, adaptation, and analysis are commonly performed with the aid of model building tools [8] and reconstruction and analysis frameworks, such as COBRA [9], COBRApy [10], RAVEN [11] or PSAMM [12]. These frameworks provide implementation of a vast scope of methods with different goals, including the reconstruction of a draft metabolic model [13], visualisation of metabolic maps (e.g., see Paint4Net [14]), identification of blocked reactions and gap filling [15] and analysis of reconstructed GEMs, such as optimal steady-state flux assessment [16] or flux sampling [17]. GEMs have been reconstructed for more than 1,000 different organisms [18]. Moreover, advances in our knowledge guide iterative refinements of GEMs. For example, Recon presents a generic human GEM that has gone through several iterations from Recon 1 [19] to Recon 2.2 [20] and to Recond3D [21], and was later extended and integrated with the HMR2.0 database [22] to obtain the Human–GEM model [23]. In the context of biomedicine, GEM applications range from the identification of disease biomarkers to the prediction of drug targets [24], drug repurposing [25] and cancer research [26]. GEMs can also be applied in a vast array of bioengineering applications [18]. These range from predicting cellular phenotypes (e.g., in the context of predicting maximal growth in different conditions and identification of an optimal medium [27]) to guiding metabolic engineering (e.g., in the context of optimal strain design [28]) and identification of a minimal gene set [29]. Most computational approaches aimed at the analysis of GEMs rely on constraint-based modelling and are based on flux balance analysis (FBA) [16] or its derivations. FBA aims to find the metabolic flux values that are consistent with a set of given constraints (minimal and maximal flux bounds) and which bring the system to a steady state. Moreover, FBA requires a specification of required metabolic functionality (RMF) that is used to define an objective function for optimisation. The optimisation can then be formulated as a linear programming (LP) problem. However, since the constraints in this formulation are usually mathematically underdetermined [30], several nonunique optimal solutions exist. To assess metabolic flux ranges through reactions that bring the system to a near optimal, or optimal, steady state, flux variability (FVA) can be used [31]. However, the latter still requires the specification of a RMF, which is hard to identify in a general context and may yield biased results. Moreover, it has been shown that the definition of the RMF strongly affects the precision of model predictions [32]. An unbiased alternative to methods relying on RMF-based optimisation is to use flux sampling of the feasible solution space without a specific optimisation criterion [17]. Reconstructed GEMs, as described above, present the metabolism of a general cell in an arbitrary context and, thus, compose generic models. Since only specific metabolic reactions are, in fact, active in a specific cell [33], these models need to be further tailored to a specific context in which only a subset of enzymes is active [34]. This process can be carried out using different reconstruction algorithms, in combination with high-throughput datasets and available biological knowledge, to obtain context-specific models (see Figure 1 and Tables 1 and 2). The latter present a subset of a generic GEM and can be used to describe the metabolism of a specific cell in a specific context [35]. Finally, such a model can describe a cell-, a tissue-, a disease-, or even an individual-specific model.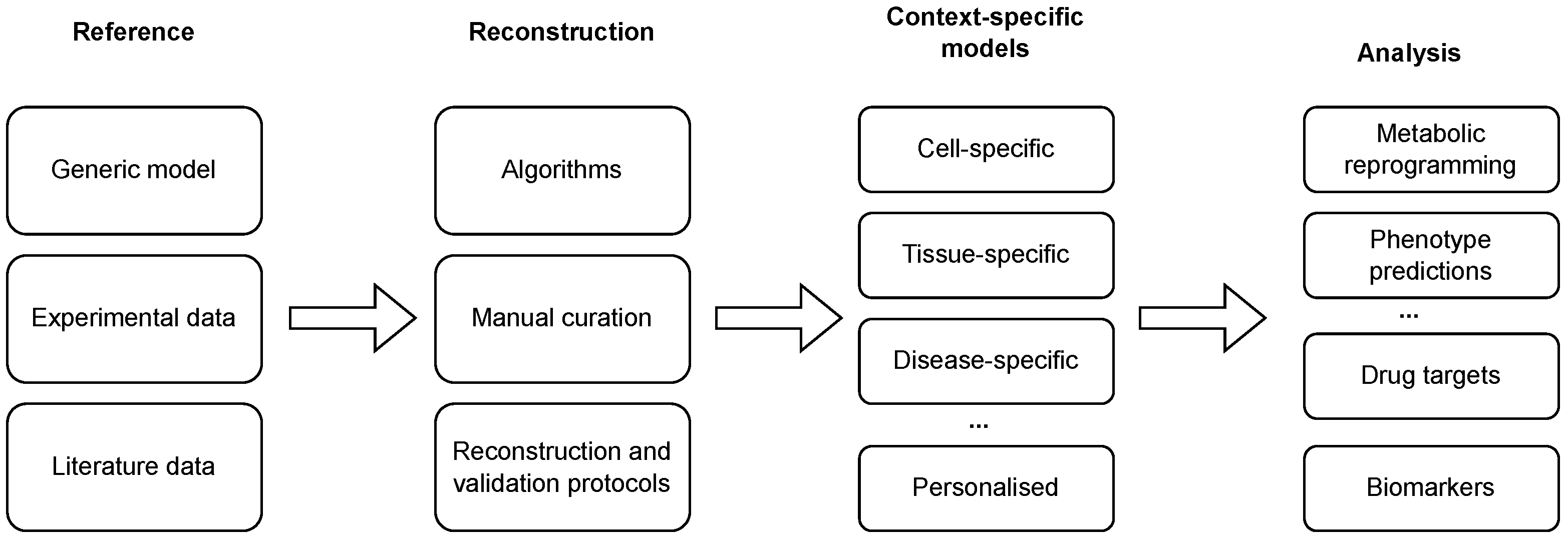
Figure 1. Reconstruction and analysis of context-specific GEMs. Generic models are tailored to a specific context with the integration of (high-throughput) experimental and literature data using a combination of automated algorithms and manual curation. The reconstruction process can be additionally enhanced with the application of reconstruction and validation protocols. The reconstructed models can be used to conduct different analyses, ranging from the prediction of phenotypes and context-specific reprogramming of a metabolic network to the identification of drug targets and disease biomarkers.
3. Algorithms and Tools for Reconstruction of Context-Specific Models
Most algorithms for the reconstruction of context-specific GEMs rely on transcriptomics data to identify active and inactive genes and to adjust metabolic reaction activities in a given context (see Table 2). In this case, each transcript and its corresponding protein/enzyme needs to be associated with specific reactions. One of the first attempts to correlate gene expression data with metabolic flux constraints was presented by Akesson et al. [36]. This was performed on a gene-by-gene basis, where fluxes through the metabolic reactions, with experimental evidence suggesting the absence of their enzymes, were constrained to 0.
Gene–protein reaction (GPR) rules present an association between a specific gene and a metabolic reaction in a model. These rules can describe different types of gene–reaction linkage. For example, different genes might encode different subunits of the same enzyme. In this case, a reaction catalysed by this enzyme can be active only when all of the respective genes are expressed (AND rule). Different genes might also express isoforms of the same enzyme. In this case, a reaction catalysed by this enzyme can be active when at least one of the respective genes is expressed (OR rule) [37]. A large number of recent algorithmic approaches for the reconstruction of context-specific GEMs rely on GPR rules to project the transcriptomics data to reaction activities. However, as illustrated above, GPR rules are encoded in a model as Boolean functions. On the other hand, gene expression data are usually described with non-binary values. In this case, logical OR can be interpreted as the maximum, and logical AND as the minimum, between two or more values (Min/Max GPR mapping) [38]. Alternatively, AND can also be interpreted as the geometric mean, and OR as the sum of two or more values [39].
Certain algorithms only require a definition of a core set of reactions, which are active in a given context. A list of such reactions can be compiled manually (e.g., see [40]) or automatically using transcriptomics data (e.g., see [41,42][41][42]). Some reconstruction algorithms allow the integration of other kinds of data, for example metabolomics or proteomics data (see Table 2).
Researchers employ and extend the classification of methods as introduced in [43]. Namely, the majority of the methods can be classified into three main families, i.e., GIMME-, iMAT-, and MBA-like families. The researchers also introduce a MADE-like family, which employs differential expression data in the reconstruction process (see Table 1 and Figure 2). An overview of the algorithms for context-specific GEM reconstruction is summarised in Table 2.
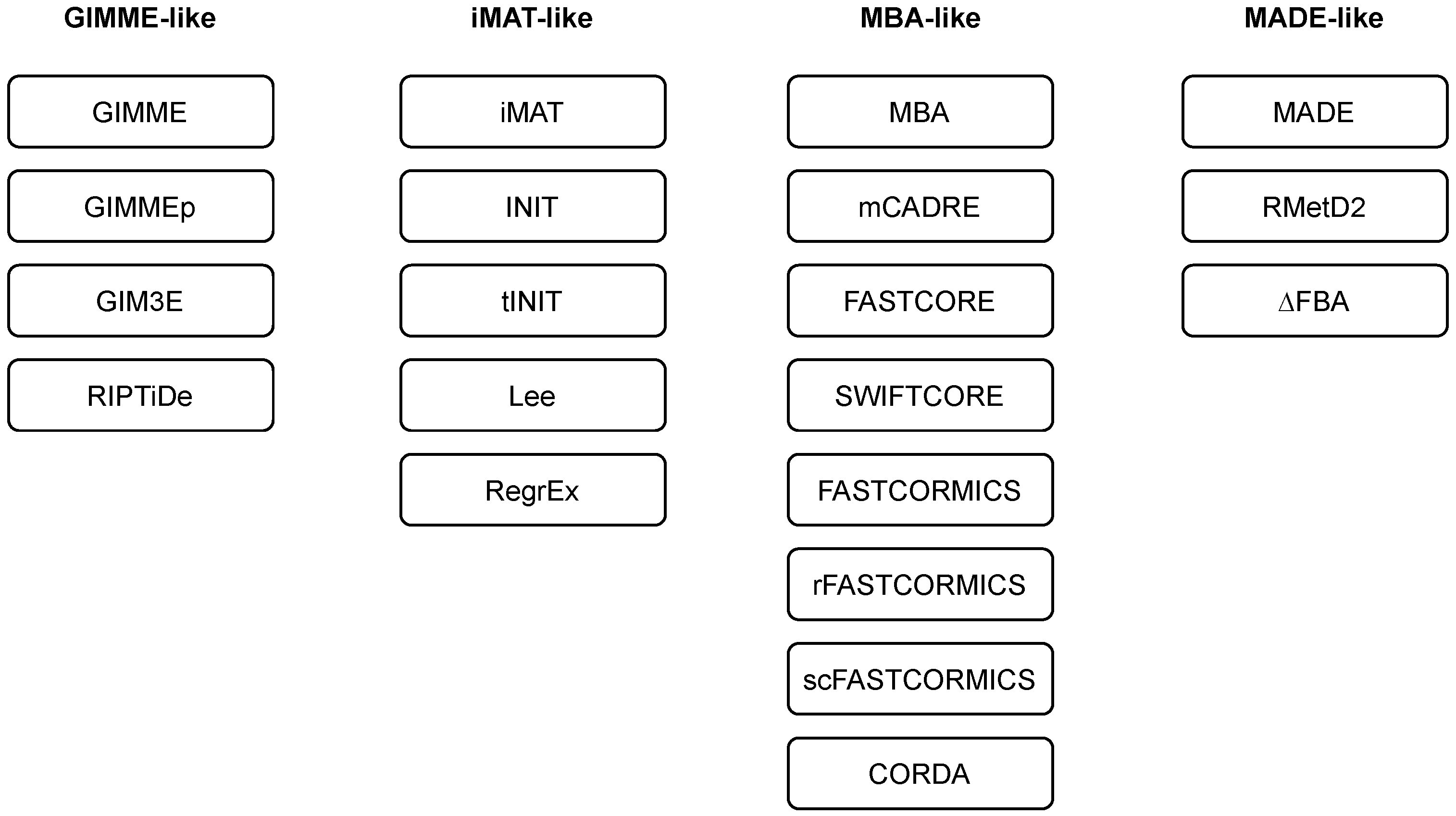

Figure 2.
Families of algorithms for automated reconstruction of context-specific models.
Table 1. An overview of different families of algorithms for context-specific model reconstruction. Abbreviations: RMF—required metabolic function; MILP–mixed integer linear programming.
| Family | Description |
|---|---|
| Employs differential gene expression data to identify flux differences between two or more conditions. | |
Table 2. An overview of algorithms for automated reconstruction of context-specific models. Abbreviations: LP—linear programming; RMF—required metabolic function.
| Algorithm | Reference | Family | Input Data | Comments | |
|---|---|---|---|---|---|
| GIMME-like | Maximising the compliance with the experimental evidence while pertaining to a given RMF. | ||||
| iMAT-like | Does not specify a RMF, matching of reactions states (active or inactive) with expression profiles (present or absent), employs MILP-based optimisation. | ||||
| GIMME | Becker et al., 2008 [38] | GIMME-like | transcriptomics | Inactivate reactions below a threshold while maintaining RMF. | |
| GIMMEp | Bordbar et al., 2012 [44] | GIMME-like | transcriptomics, proteomics | RMFs based on proteomics data. | |
| MBA-like | Defining core reactions and removing other reactions while pertaining to model consistency, support integration of different data types. | ||||
| GIM3E | Schmidt et al., 2013 [45] | GIMME-like | transcriptomics, metabolomics | No thresholding. | MADE-like |
| RIPTiDe | Jenior et al., 2020 [46] | GIMME-like | transcriptomics | Minimises the weighted flux values, no thresholding. | |
| iMAT | Zur et al., 2010 [47] | iMAT-like | transcriptomics, proteomics | Matches reaction activities with expression profiles, no RMF. | |
| INIT | Agren et al., 2012 [48] | iMAT-like | transcriptomics, proteomics, metabolomics (qualitative) | Reaction weights based on experimental evidence, integration of metabolomics data. | |
| tINIT | Agren et al., 2014 [49] | iMAT-like | prior knowledge, transcriptomics, proteomics, metabolomics (qualitative) | Based on a set of required metabolic tasks. | |
| Lee | Lee et al., 2012 [50] | iMAT-like | transcriptomics | Uses absolute expression data (RNA-seq). | |
| RegrEx | Estevez et al., 2015 [51] | iMAT-like | transcriptomics | Uses absolute expression data (RNA-seq) and regularisation. | |
| MBA | Jerby et al., 2010 [52] | MBA-like | prior knowledge, transcriptomics, proteomics, metabolomics, fluxomics | Removes non-core reactions and checks model consistency for core reactions. | |
| mCADRE | Wang et al., 2012 [53] | MBA-like | transcriptomics, metabolomics | Different reaction scores to determine core reactions. | |
| FASTCORE | Vlassis et al., 2014 [40] | MBA-like | a set of core reactions | Two LPs to find a minimal set of non-core reactions to activate all core reactions. | |
| SWIFTCORE | Tefagh and Boyd, 2020 [54] | MBA-like | a set of core reactions | Enhanced runtime and network compactness in comparison to FASTCORE. | |
| FASTCORMICS | Pires Pacheco at al., 2015 [41] | MBA-like | transcriptomics | FASTCORE workflow for microarray data. | |
| rFASTCORMICS | Pires Pacheco at al., 2019 [42] | MBA-like | transcriptomics | FASTCORE workflow for RNA-seq data. | |
| scFASTCORMICS | Pires Pacheco at al., 2022 [55] | MBA-like | transcriptomics | FASTCORE workflow for scRNA-seq data. | |
| CORDA | Schultz and Qutub, 2016 [34] | MBA-like | a set of core reactions | Does not require to remove all non-core reactions. | |
| MADE | Jensen and Papin, 2011 [56] | MADE-like | transcriptomics | Identifies reaction activities in a sequence of measurements. | |
| RMetD2 | Zhang et al., 2019 [57] | MADE-like | transcriptomics | Sequentially pushes the constraints. | |
| ΔFBA | Ravi et al., 2021 [58] | MADE-like | transcriptomics | Finds a consistent and minimal solution of flux differences between the conditions. |
References
- Zhang, C.; Hua, Q. Applications of genome-scale metabolic models in biotechnology and systems medicine. Front. Physiol. 2016, 6, 413.
- Lewis, N.E.; Nagarajan, H.; Palsson, B.O. Constraining the metabolic genotype–phenotype relationship using a phylogeny of in silico methods. Nat. Rev. Microbiol. 2012, 10, 291–305.
- O’brien, E.J.; Lerman, J.A.; Chang, R.L.; Hyduke, D.R.; Palsson, B.Ø. Genome-scale models of metabolism and gene expression extend and refine growth phenotype prediction. Mol. Syst. Biol. 2013, 9, 693.
- Maarleveld, T.R.; Khandelwal, R.A.; Olivier, B.G.; Teusink, B.; Bruggeman, F.J. Basic concepts and principles of stoichiometric modeling of metabolic networks. Biotechnol. J. 2013, 8, 997–1008.
- Nilsson, A.; Nielsen, J. Genome scale metabolic modeling of cancer. Metab. Eng. 2017, 43, 103–112.
- Moolamalla, S.; Vinod, P. Genome-scale metabolic modelling predicts biomarkers and therapeutic targets for neuropsychiatric disorders. Comput. Biol. Med. 2020, 125, 103994.
- Thiele, I.; Palsson, B.Ø. A protocol for generating a high-quality genome-scale metabolic reconstruction. Nat. Protoc. 2010, 5, 93–121.
- Mendoza, S.N.; Olivier, B.G.; Molenaar, D.; Teusink, B. A systematic assessment of current genome-scale metabolic reconstruction tools. Genome Biol. 2019, 20, 1–20.
- Heirendt, L.; Arreckx, S.; Pfau, T.; Mendoza, S.N.; Richelle, A.; Heinken, A.; Haraldsdóttir, H.S.; Wachowiak, J.; Keating, S.M.; Vlasov, V.; et al. Creation and analysis of biochemical constraint-based models using the COBRA Toolbox v. 3.0. Nat. Protoc. 2019, 14, 639–702.
- Ebrahim, A.; Lerman, J.A.; Palsson, B.O.; Hyduke, D.R. COBRApy: Constraints-based reconstruction and analysis for python. BMC Syst. Biol. 2013, 7, 1–6.
- Wang, H.; Marcišauskas, S.; Sánchez, B.J.; Domenzain, I.; Hermansson, D.; Agren, R.; Nielsen, J.; Kerkhoven, E.J. RAVEN 2.0: A versatile toolbox for metabolic network reconstruction and a case study on Streptomyces coelicolor. PLoS Comput. Biol. 2018, 14, e1006541.
- Steffensen, J.L.; Dufault-Thompson, K.; Zhang, Y. PSAMM: A portable system for the analysis of metabolic models. PLoS Comput. Biol. 2016, 12, e1004732.
- Karlsen, E.; Schulz, C.; Almaas, E. Automated generation of genome-scale metabolic draft reconstructions based on KEGG. BMC Bioinf. 2018, 19, 1–11.
- Kostromins, A.; Stalidzans, E. Paint4Net: COBRA Toolbox extension for visualization of stoichiometric models of metabolism. Biosystems 2012, 109, 233–239.
- Pan, S.; Reed, J.L. Advances in gap-filling genome-scale metabolic models and model-driven experiments lead to novel metabolic discoveries. Curr. Opin. Biotechnol. 2018, 51, 103–108.
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248.
- Herrmann, H.A.; Dyson, B.C.; Vass, L.; Johnson, G.N.; Schwartz, J.M. Flux sampling is a powerful tool to study metabolism under changing environmental conditions. NPJ Syst. Biol. Appl. 2019, 5, 32.
- Ye, C.; Wei, X.; Shi, T.; Sun, X.; Xu, N.; Gao, C.; Zou, W. Genome-scale metabolic network models: From first-generation to next-generation. Appl. Microbiol. Biotechnol. 2022, 106, 4907–4920.
- Duarte, N.C.; Becker, S.A.; Jamshidi, N.; Thiele, I.; Mo, M.L.; Vo, T.D.; Srivas, R.; Palsson, B.Ø. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc. Natl. Acad. Sci. USA 2007, 104, 1777–1782.
- Swainston, N.; Smallbone, K.; Hefzi, H.; Dobson, P.D.; Brewer, J.; Hanscho, M.; Zielinski, D.C.; Ang, K.S.; Gardiner, N.J.; Gutierrez, J.M.; et al. Recon 2.2: From reconstruction to model of human metabolism. Metabolomics 2016, 12, 109.
- Brunk, E.; Sahoo, S.; Zielinski, D.C.; Altunkaya, A.; Dräger, A.; Mih, N.; Gatto, F.; Nilsson, A.; Preciat Gonzalez, G.A.; Aurich, M.K.; et al. Recon3D enables a three-dimensional view of gene variation in human metabolism. Nat. Biotechnol. 2018, 36, 272–281.
- Mardinoglu, A.; Agren, R.; Kampf, C.; Asplund, A.; Uhlen, M.; Nielsen, J. Genome-scale metabolic modelling of hepatocytes reveals serine deficiency in patients with non-alcoholic fatty liver disease. Nat. Commun. 2014, 5, 3083.
- Robinson, J.L.; Kocabaş, P.; Wang, H.; Cholley, P.E.; Cook, D.; Nilsson, A.; Anton, M.; Ferreira, R.; Domenzain, I.; Billa, V.; et al. An atlas of human metabolism. Sci. Signal. 2020, 13, eaaz1482.
- Bintener, T.; Pacheco, M.P.; Kishk, A.; Didier, J.; Sauter, T. Drug Target Prediction Using Context-Specific Metabolic Models Reconstructed from rFASTCORMICS. In Cancer Drug Resistance; Springer: Berlin/Heidelberg, Germany, 2022; pp. 221–240.
- Tomi-Andrino, C.; Pandele, A.; Winzer, K.; King, J.; Rahman, R.; Kim, D.H. Metabolic modeling-based drug repurposing in Glioblastoma. Sci. Rep. 2022, 12, 11189.
- Barata, T.; Vieira, V.; Rodrigues, R.; das Neves, R.P.; Rocha, M. Reconstruction of tissue-specific genome-scale metabolic models for human cancer stem cells. Comput. Biol. Med. 2022, 142, 105177.
- Song, H.; Kim, T.Y.; Choi, B.K.; Choi, S.J.; Nielsen, L.K.; Chang, H.N.; Lee, S.Y. Development of chemically defined medium for Mannheimia succiniciproducens based on its genome sequence. Appl. Microbiol. Biotechnol. 2008, 79, 263–272.
- Jiang, S.; Otero-Muras, I.; Banga, J.R.; Wang, Y.; Kaiser, M.; Krasnogor, N. OptDesign: Identifying Optimum Design Strategies in Strain Engineering for Biochemical Production. ACS Synth. Biol. 2022, 11, 1531–1541.
- Lachance, J.C.; Matteau, D.; Brodeur, J.; Lloyd, C.J.; Mih, N.; King, Z.A.; Knight, T.F.; Feist, A.M.; Monk, J.M.; Palsson, B.O.; et al. Genome-scale metabolic modeling reveals key features of a minimal gene set. Mol. Syst. Biol. 2021, 17, e10099.
- Loghmani, S.B.; Veith, N.; Sahle, S.; Bergmann, F.T.; Olivier, B.G.; Kummer, U. Inspecting the Solution Space of Genome-Scale Metabolic Models. Metabolites 2022, 12, 43.
- Mahadevan, R.; Schilling, C.H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276.
- García, M.M.; Pacheco, M.; Bintener, T.; Presta, L.; Sauter, T. Importance of the biomass formulation for cancer metabolic modeling and drug prediction. iScience 2021, 24, 103110.
- Uhlén, M.; Fagerberg, L.; Hallström, B.M.; Lindskog, C.; Oksvold, P.; Mardinoglu, A.; Sivertsson, Å.; Kampf, C.; Sjöstedt, E.; Asplund, A.; et al. Tissue-based map of the human proteome. Science 2015, 347, 1260419.
- Schultz, A.; Qutub, A.A. Reconstruction of Tissue-Specific Metabolic Networks Using CORDA. PLoS Comput. Biol. 2016, 12, 1–33.
- Opdam, S.; Richelle, A.; Kellman, B.; Li, S.; Zielinski, D.C.; Lewis, N.E. A systematic evaluation of methods for tailoring genome-scale metabolic models. Cell Syst. 2017, 4, 318–329.
- Åkesson, M.; Förster, J.; Nielsen, J. Integration of gene expression data into genome-scale metabolic models. Metab. Eng. 2004, 6, 285–293.
- Di Filippo, M.; Damiani, C.; Pescini, D. GPRuler: Metabolic gene-protein-reaction rules automatic reconstruction. PLoS Comput. Biol. 2021, 17, e1009550.
- Becker, S.A.; Palsson, B.O. Context-specific metabolic networks are consistent with experiments. PLoS Comput. Biol. 2008, 4, e1000082.
- Grausa, K.; Mozga, I.; Pleiko, K.; Pentjuss, A. Integrative Gene Expression and Metabolic Analysis Tool IgemRNA. Biomolecules 2022, 12, 586.
- Vlassis, N.; Pacheco, M.P.; Sauter, T. Fast Reconstruction of Compact Context-Specific Metabolic Network Models. PLoS Comput. Biol. 2014, 10, 1–10.
- Pacheco, M.P.; John, E.; Kaoma, T.; Heinäniemi, M.; Nicot, N.; Vallar, L.; Bueb, J.L.; Sinkkonen, L.; Sauter, T. Integrated metabolic modelling reveals cell-type specific epigenetic control points of the macrophage metabolic network. BMC Genom. 2015, 16, 809.
- Pacheco, M.P.; Bintener, T.; Ternes, D.; Kulms, D.; Haan, S.; Letellier, E.; Sauter, T. Identifying and targeting cancer-specific metabolism with network-based drug target prediction. EBioMedicine 2019, 43, 98–106.
- Robaina Estévez, S.; Nikoloski, Z. Generalized framework for context-specific metabolic model extraction methods. Front. Plant Sci. 2014, 5, 491.
- Bordbar, A.; Mo, M.L.; Nakayasu, E.S.; Schrimpe-Rutledge, A.C.; Kim, Y.M.; Metz, T.O.; Jones, M.B.; Frank, B.C.; Smith, R.D.; Peterson, S.N.; et al. Model-driven multi-omic data analysis elucidates metabolic immunomodulators of macrophage activation. Mol. Syst. Biol. 2012, 8, 558.
- Schmidt, B.J.; Ebrahim, A.; Metz, T.O.; Adkins, J.N.; Palsson, B.Ø.; Hyduke, D.R. GIM3E: Condition-specific models of cellular metabolism developed from metabolomics and expression data. Bioinformatics 2013, 29, 2900–2908.
- Jenior, M.L.; Moutinho, T.J., Jr.; Dougherty, B.V.; Papin, J.A. Transcriptome-guided parsimonious flux analysis improves predictions with metabolic networks in complex environments. PLoS Comput. Biol. 2020, 16, 1–26.
- Zur, H.; Ruppin, E.; Shlomi, T. iMAT: An integrative metabolic analysis tool. Bioinformatics 2010, 26, 3140–3142.
- Agren, R.; Bordel, S.; Mardinoglu, A.; Pornputtapong, N.; Nookaew, I.; Nielsen, J. Reconstruction of genome-scale active metabolic networks for 69 human cell types and 16 cancer types using INIT. PLoS Comput. Biol. 2012, 8, e1002518.
- Agren, R.; Mardinoglu, A.; Asplund, A.; Kampf, C.; Uhlen, M.; Nielsen, J. Identification of anticancer drugs for hepatocellular carcinoma through personalized genome-scale metabolic modeling. Mol. Syst. Biol. 2014, 10, 721.
- Lee, D.; Smallbone, K.; Dunn, W.B.; Murabito, E.; Winder, C.L.; Kell, D.B.; Mendes, P.; Swainston, N. Improving metabolic flux predictions using absolute gene expression data. BMC Syst. Biol. 2012, 6, 73.
- Robaina Estévez, S.; Nikoloski, Z. Context-specific metabolic model extraction based on regularized least squares optimization. PLoS ONE 2015, 10, e0131875.
- Jerby, L.; Shlomi, T.; Ruppin, E. Computational reconstruction of tissue-specific metabolic models: Application to human liver metabolism. Mol. Syst. Biol. 2010, 6, 401.
- Wang, Y.; Eddy, J.A.; Price, N.D. Reconstruction of genome-scale metabolic models for 126 human tissues using mCADRE. BMC Syst. Biol. 2012, 6, 153.
- Tefagh, M.; Boyd, S.P. SWIFTCORE: A tool for the context-specific reconstruction of genome-scale metabolic networks. BMC Bioinf. 2020, 21, 140.
- Pacheco, M.P.; Ji, J.; Prohaska, T.; García, M.M.; Sauter, T. scFASTCORMICS: A Contextualization Algorithm to Reconstruct Metabolic Multi-Cell Population Models from Single-Cell RNAseq Data. Metabolites 2022, 12, 1211.
- Jensen, P.A.; Papin, J.A. Functional integration of a metabolic network model and expression data without arbitrary thresholding. Bioinformatics 2011, 27, 541–547.
- Zhang, C.; Lee, S.; Bidkhori, G.; Benfeitas, R.; Lovric, A.; Chen, S.; Uhlen, M.; Nielsen, J.; Mardinoglu, A. RMetD2: A tool for integration of relative transcriptomics data into Genome-scale metabolic models. BioRxiv 2019.
- Ravi, S.; Gunawan, R. ΔFBA—Predicting metabolic flux alterations using genome-scale metabolic models and differential transcriptomic data. PLoS Comput. Biol. 2021, 17, 1–18.
More
