Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Peter Tang and Version 1 by Dongqin Ni.
In a random laser (RL), optical feedback arises from multiple scattering instead of conventional mirrors. RLs generate a laser-like emission, and meanwhile take advantage of a simpler and more flexible laser configuration. The applicability of RLs as light sources and optical sensors has been proved.
- random lasing
- light scattering
- light source
- optical sensor
1. Random Laser (RL) Emission Properties
RL emission shows certain properties, including the properties of a lasing threshold, peak wavelength and coherence. In addition to the common laser spectral properties, such as the linewidth narrowing and intensity enhancement over the lasing threshold, RL also exhibits properties such as a tunable peak wavelength and tunable coherence. The investigated influence factors of RL emissions vary from author to author [77][1]. Table 1 summarizes the five general influence factors of the RL emission properties, with examples for each.
Table 1.
Different influence factors of the RL emission properties.
|
RL Emission Properties |
Influence Factors |
Experimental Parameters |
|---|---|---|
|
Lasing threshold Tunability Coherence |
Illumination |
pump temporal profile (pulse duration) [78,79,80,81][2][3][4][5] |
|
pump spatial profile (size and shape) [14,[4]54,[6]80,[7]82,[8]83,[9]84,[10]85,[86,87,11][88]12][13][14] |
||
|
Scatterers |
||
|
Dye |
||
|
Solvent |
||
|
Collection |
2. Lasing Threshold Characterization and Reduction
The lasing threshold, an important RL property, has been thoroughly investigated. The threshold can be characterized by an increased emission intensity or narrowed spectral line width. In addition to the traditional method in frequency spectra, the RL threshold can also be determined by measuring temporal profiles [95][31]. The building time of an RL pulse is apparently shortened around the threshold due to the increased gain of the stimulated emission upon crossing the threshold. Another particular RL property is that the shot-by-shot emission intensity fluctuates under the same experimental conditions. This property can be used to assess the lasing threshold too.
A statistical measurement of the fluctuated intensity indicates an intriguing distribution change: a change from Gaussian to Lévy shape at the onset of the RL threshold, thus providing another identifier of the threshold [96][32]. Interestingly, an intrinsic threshold regime rather than a threshold point was revealed [97][33]. In this threshold regime, a progressive growth in the coherent field caused by the stimulated emission was observed [97][33]. Such a progressively smoother transition was more frequently observed in a micro-/nano-laser than in a macroscopic laser [98][34]. A further statistical analysis of the fluctuation correlation among the above RL spectrum replicas resulted in a replica symmetry breaking (RSB) observation around the threshold [99][35]. RSB is a state-of-the-art method for predicting a phase transition of a complex system and reveals the interplay between the disorders of and fluctuations in the system [100][36]. In the case of RLs, the phase transition refers to a transition from a non-lasing to lasing state. The revealed interplay is the one between the multiple scattering and the quantum noises (e.g., spontaneous emission) responsible for the start of the lasing.
In an RL, the peculiar optical feedback and extreme light leakage at boundaries contribute to the inefficient gain–loss balance around the threshold, leading to a high-threshold RL emission. Currently, the research focus of the RL threshold is on its reduction. This is significant because the high-threshold laser emission usually hinders the further applicability of RLs; for example, applications in the biological field where the excitation intensity is required to be low to avoid photo-toxicity to tissues. In this regard, changing the shape of scatterers to increase the surface area [12][21] or optimizing the size of scatterers [92][22] can facilitate the scattering efficiency and, therefore, lower the RL threshold. In other reports, additional disorders were introduced into a spatial distribution of pump light to lower the RL threshold [84,85][10][11]. The RL threshold can also be lowered by employing metal nanoparticles (NPs), in which, the surface plasmon resonance can enable a high gain for lasing even at a low excitation intensity [16,60,92,101,102,103][22][29][37][38][39][40]. Furthermore, external optical cavities such as the fiber structure [47[28][30][41],94,104], FP cavity [39,105,106,107,108,109][42][43][44][45][46][47] and WGM cavity [38,110][48][49] were proposed to enhance the optical feedback of RLs and eventually reduce the lasing threshold.
3. Peak Wavelength Shift (Tunability)
A shifted peak wavelength is usually observed in the spectra of dye-based RLs [111][50]. In a pure dye solution, the peak wavelength redshift was ascribed to dye aggregates [112][51] or dye reabsorption [113][52]. Dye aggregates are formed at higher concentrations, leading to a second spectral band at the longer wavelength side, i.e., redshift [112][51]. Dye reabsorption happens because of the overlap between the absorption and emission spectra of dyes, known as a secondary inner filter effect [113][52]. It was reported that when the fluorescent dye without spectral overlap was applied, no redshift due to reabsorption and re-emission was observed in the pure dye solution [113][52]. The above two effects were employed to explain the most redshift observed in the dye-based RLs [52,114,115][53][54][55]. Depending on the experimental configurations, both enhanced redshift (relative redshift) and weakened redshift (relative blueshift) are observed. The details are discussed as follows.
3.1. Relative Redshift Realization
Increasing scatterer concentrations is a common approach for inducing a relative redshift [52,111][50][53]. A stronger scattering strength leads to a longer light dwell path where the fluorescence reabsorption and re-emission effect occurs [115][55]. Hence, a stronger redshift (relative redshift) is expected. In turn, the peak redshift can be used to characterize the light path length [52][53]. In a further step, the peak shift has the potential for the detection of variations in the scattering or absorption strength. For instance, Ignesti et al. [111][50] reported a maximum redshift of around 50 nm when increasing concentrations of intralipid in a dye solution. Other approaches, such as using larger microspheres diameters [116][56] and increasing the laser cavity lengths [117][57], also facilitate the peak wavelength redshift.
3.2. Relative Blueshift Realization
On the contrary, El-Dardirya and Lagendijk [118][58] demonstrated a blueshift by increasing concentrations of non-fluorescent absorbers in an RL medium. This is expected as the light path in the gain medium is reduced by the absorption. This results in a weak reabsorption and reemission effect (relative blueshift). Another blueshift phenomenon was observed in a simulation case when pump energy was well above the lasing threshold. This was explained by the depletion of the ground state, which pulls the peak emission towards smaller wavelengths for a stronger amplification. Intriguingly, increasing scattering can induce a relative blueshift rather than redshift. For instance, the blueshift was observed when increasing concentrations of TiO2 scatterers in Rhodamine B (RhB) [119][59] or in Rhodamine 6G (R6G) [93][24] methanol solution. Likewise, Hohmann et al. [52][53] reported a slight blueshift at a relatively high concentration of intralipid scatterers in an R6G water solution.
The reasons for blueshift when increasing the scattering strength are not clear in the literature. Hohmann et al. [52][53] ascribed the blueshift to the falling numbers of optimal lasing microcavities. Because the scattering mean free path ls at relatively strong scattering media is too short to construct optimal microcavities, the total light path length is reduced so that the blueshift happens. Others [119][59] believed that the lasing peak was pulled towards the shorter wavelength side to obtain a maximum gain. Bavali et al. [113][52] provided another aspect to explain the blueshift. As concentrations of scatterers increase, the overlapping area of dye absorption and emission spectra shrinks such that the redshift is saturated. A further increment of scatterers in saturated media gives rise to the encirclement of dye molecules. This has an equivalent effect to reducing dye concentrations, so blueshift occurs due to the weak reabsorption effect. This argument of blueshift might be evidenced in experiments [93,119][24][59] where, in a saturated medium with sufficiently high concentrations of dyes, only blueshift occurs when increasing the concentrations of scatterers.
4. Coherence
RLs show spatial and temporal coherence similar to a conventional laser. Spatial (temporal) coherence describes the correlation of waves at different points in space (time). On the one hand, an RL temporal coherence measurement was performed in the Michelson (Twyman–Green) interferometer [120,121][60][61]. Under the common RL configuration with single-shot excitation, titled mirrors were proposed in the Michelson interferometer to give enough of a path delay along the mirrors for the temporal measurements [120][60]. On the other hand, the Young’s double slit interferometric scheme was utilized for the measurement of the RL spatial coherence [83,121][9][61]. A low spatial coherence of RL emission was reported during the measurement [122][62]. Regarding the RL coherence, the characteristics of spectral modes are discussed in detail in the following, as well as the corresponding origins of the spatial modes.
4.1. Characteristics of Spectral Modes
From the point of view of spectral modes, the observed RL emission is classified into two types. One is an incoherent feedback RL emission characterized by a single continuous spectrum with a linewidth of a few nanometers. The other is a coherent feedback RL emission characterized by a spectrum comprising multiple discrete modes, each with a linewidth of sub-nanometers [63].
The different characteristics of RL spectra have been previously explained by Cao et al. [63] from the macroscopic perspective of the feedback mechanism: the former spectrum is attributed to the incoherent (non-resonant, intensity or energy) feedback where the light propagates along open trajectories. The latter one arises from the coherent (resonant, field or amplitude) feedback where the emitted light returns to the position that it has visited before. An optically closed loop is formed through the coherent feedback mechanism, resulting in light interference and light confinement. Due to the wavelength-sensitive interference effect, only light of certain wavelengths can be confined in such a cavity [63]. This is analogous to the conventional lasers, in which, the cavity changes the frequency of the emission light, as well as the directionality.
The lack of multiple modes in the incoherent feedback RL spectra was assumed by Cao et al. [63] to be a lack of lasing cavities or interference. In contrast, another assumption was that the interference in an incoherent feedback RL exists, but the interference effect is averaged out because the lasing cavities overlap in the spatial region [2,41][64][65]. It was found that the presence and even the number of multiple modes highly depend on the experimental conditions. For instance, a transition from an incoherent feedback RL to the coherent feedback RL was induced by reducing the pump spot size [80,82][4][8] or using a pump pulse duration of a picosecond instead of nanosecond [79,80][3][4]. In this way, the mode overlapping in either the spatial domain or time domain is reduced so that the individual modes can be visualized. From the perspective of scattering, increasing the refractive index difference between the scatterers and solvent [123][66] or increasing the scatterer concentration [63] also gives rise to the easy realization of a coherent feedback RL. The detection angle can also affect the spectral mode visualization. The disappearance of spectral modes was observed when the detection angle was increased on a polymeric capillary system doped with quantum dots [124][67].
Other effects, such as mode repulsion and coupling, can also change the RL spectral modes profile [81,125,126][5][68][69]. As a complex system, RLs are also suitable for the generation of non-linear optics, which, in turn, induces alterations to the RL spectral modes [127][70]. One of the contributed non-linear optics is the stimulated Raman scattering.
4.2. Characteristics of Spatial Modes
To understand the origin of the spectral modes, the spatial modes of the system need to be studied initially. The spatial modes can be localized modes when the scattering is strong enough in the Anderson localization regime [88,128][14][71]. (Light localization originates from the wave interference between multiple scattering paths. To distinguish from the weak localization in the light diffusion regime, the wave interference influence in the Anderson localization regime—in which, the light diffusion is absent due to the extremely strong scattering—is also called strong localization [129][72].) However, most of the RL systems are in the diffusive regime. In a passive (without gain) diffusive sample, the extended modes cover the entire system and overlap with each other [41,66][65][73]. Due to the overlapping, it is more likely that extended modes are averaged out, leading to a continuous RL spectrum. This is the characteristic of incoherent feedback RLs. A numerical model using light diffusion with gain can explain and predict this phenomenon [2,5][64][74]. However, this model does not predict multiple modes since the phase of light field and interference effect are neglected here. Therefore, other models have been introduced to describe how the spatial modes influence the spectral modes in the diffusive regime.
Figure 21 summarizes the RL modes models in a light diffusive regime. These models can mainly be divided into two groups: one is based on extended modes, such as the model of amplified extended modes [130][75] and the model of absorption-induced confinement [131][76]; the other one is based on anomalously localized modes, such as the model of prelocalized modes [132,133][77][78]. The detailed explanations are given as follows.
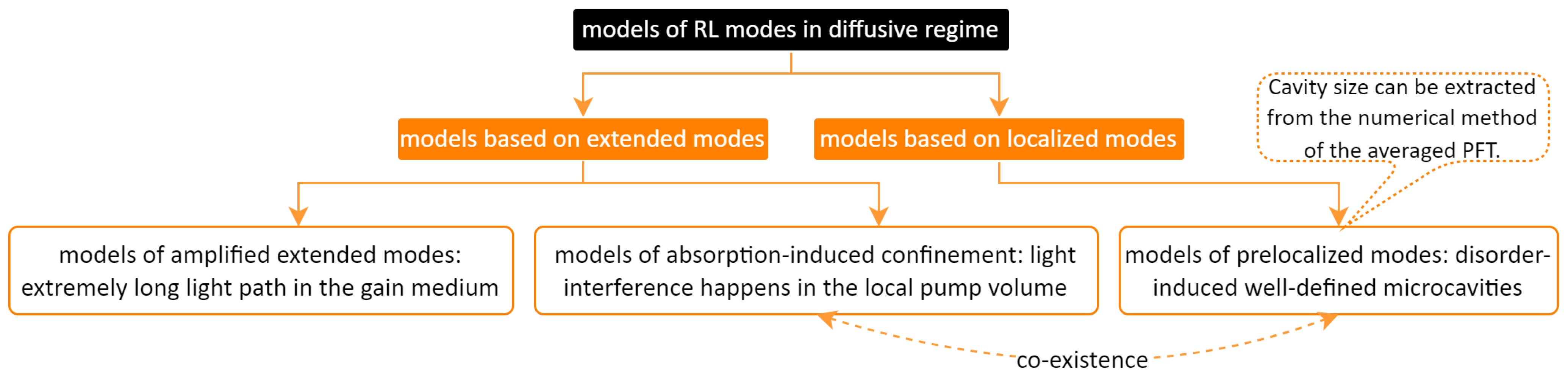
Figure 21.
Summary of the models of RL spatial modes in the light diffusive regime.
Amplified Extended Modes
In the simulation from Mujumdar et al. [130][75] using the Monte Carlo technique, lasing modes are amplified extended modes. They argued that certain single spontaneous emissions experience extremely long light paths by chance and are consequently amplified to form multiple modes. These extremely long light paths are rare in a passive system and therefore distinct in the RL spectra once they are selected by gain. The author also used the model to explain another experimental phenomenon, where the positions of multiple modes are different in the single-shot excitation. In other words, the multiple modes are random spikes rather than regular discrete peaks. They ascribed the chaotic behavior to the inherent randomness of spontaneous emission.
Absorption-Induced Confined Modes
In the numerical study of Yamilov et al. [131][76] using the finite-difference time-domain method, light confinement is attributed to the optical absorption, e.g., reabsorption from Rhodamine dyes, which limits the number of extended modes to lase. More specifically, the reabsorption effect can suppress the feedback from the unpumped part such that the lasing modes can be confined in the pumped volume. Since the spatial averaging effect is diminished by local pumping, the modes are present on the spectrum. The lasing modes within the effective volume are still the same extended modes as those in a passive system. However, the appearance of the lasing modes depends on the local pumping, e.g., the pumping spot size. In a rather weak scattering system, a regular FP-like cavity is even formed between the base and tip of the pumping cone [134][79].
Although the amplified extended modes and absorption-induced modes both originate from the extended modes of passive systems, the feedback mechanisms are different. In the latter one, a regular lasing cavity is formed due to the absorption outside the pump area leading to the correlated spectral modes, whereas no optical cavities exist in the former case and random spikes are formed due to the intrinsic randomness of spontaneous emission. Thereby, some authors [134,135,136][79][80][81] argued that the emission with stochastic spikes is not laser emission but is amplified spontaneous emission [136][81].
Prelocalized Modes and Size Calculation of the Prelocalized Cavity
The scenario of the optical cavity by simply being scattered from one scatterer to another was doubted for the reason that scatterers could also scatter the light out of the cavity and break the closed loop [132][77]. Hence, other models suggest that multiple modes are still generated from light interference in analogy to the localized modes in the Anderson localization regime, although there are much fewer localized modes than extended modes in the diffusive regime. This anomalously localized mode in the diffusive regime is named the prelocalized mode by Apalkov et al. [132][77].
Apalkov et al. modeled the scatterers into a ring-shaped waveguide structure, along which, a higher dielectric constant is present and the prelocalized modes are generated [132][77]. The likelihood of such ring-shaped microcavities with a fixed size crucially depends on the scatterer’s size [132,133][77][78]. Specifically, when the scatterer’s size is larger, the probability of cavity formation is enhanced and the number of scatterers required to form such a cavity is reduced [133][78]. The ring microcavity here is a simple model for the lasing cavity that is formed due to disorders, which is the same as the simplified model of the FP cavity for the absorption-induced cone volume.
The scenario of disorder-induced ring microcavities was proved by Polson et al. in π-conjugated polymer films with [6][82] or without [137][83] TiO2 doping. In these films, the inhomogeneity of the film thickness contributes to the long-range fluctuation in the refractive index. The refractive index difference between the microcavity and surrounding space further facilitates the scattering strength and therefore confines the light. Meanwhile, the existence of short-range disorder induced by individual scatterers suppresses the ability of the most random cavities to trap light, e.g., scatters the light out of the microcavities such that the survived long-range cavities are sparse and consequently almost identical [6][82]. A highly correlated RL spectrum with regular modes is generated. Although the single-shot RL spectrum is highly reproducible both in powders (Anderson localization regime) [63] and in polymer films (diffusive regime) [6][82], the lasing mechanism is different. One emission line from one localized cavity is detected in powder systems, whereas one prelocalized cavity in polymer films generates numerous correlated emission lines due to its larger size.
Cao et al. [138][84] investigated the prelocalized modes using spectrally resolved speckle analysis in both a dyed micro-particles polymer system and a semiconductor NPs system. They claimed that the size of the prelocalized mode varies and decreases when the scattering strength moves towards the Anderson localization regime. In other words, the size of the prelocalized mode in the diffusive regime is larger than the size of the localized mode in the Anderson localization regime. This larger cavity size in the diffusive regime agrees with the argument from Polson et al. [6][82], as mentioned above. In addition, the cavity size is independent of the pump intensity and pump area, indicating that the lasing mode is the intrinsic property of the passive system and only relates to the scattering strength. Note that Cao [64][85] later pointed out that the model of absorption-induced confinement does not contradict the model of prelocalized modes: the local pumping does not eliminate the possibility of prelocalized modes and these two models can be simultaneously applied when the prelocalized modes happen within the effective volume induced by the local pumping.
The sizes of the above prelocalized cavities can be characterized by the averaged power fourier transform (PFT) method. The averaged PFT reveals the universality of the hidden cavities among different scattering systems, such as the R6G infiltrated opals, polymers, scatters and chicken breast [25][86]. In detail, the size of the dominant cavity can be scaled with the transport mean free path lt among different scattering systems. This indicates again that the microcavity or prelocalized mode is not an artifact; rather, it is induced and only influenced by the multiple scattering despite the varieties of scattering systems [25][86].
References
- van der Molen, K.L.; Mosk, A.P.; Lagendijk, A. Quantitative analysis of several random lasers. Opt. Commun. 2007, 278, 110–113.
- Van Der Molen, K.L.; Mosk, A.P.; Lagendijk, A. Intrinsic intensity fluctuations in random lasers. Phys. Rev. A At. Mol. Opt. Phys. 2006, 74, 53808.
- Zhai, T.; Zhou, Y.; Chen, S.; Wang, Z.; Shi, J.; Liu, D.; Zhang, X. Pulse-duration-dependent and temperature-tunable random lasing in a weakly scattering structure formed by speckles. Phys. Rev. A At. Mol. Opt. Phys. 2010, 82, 23824.
- Leonetti, M.; López, C. Active subnanometer spectral control of a random laser. Appl. Phys. Lett. 2013, 102, 71105.
- Ignesti, E.; Tommasi, F.; Fini, L.; Lepri, S.; Radhalakshmi, V.; Wiersma, D.; Cavalieri, S. Experimental and theoretical investigation of statistical regimes in random laser emission. Phys. Rev. A 2013, 88, 33820.
- Ling, Y.; Cao, H.; Burin, A.L.; Ratner, M.A.; Liu, X.; Chang, R.P. Investigation of random lasers with resonant feedback. Phys. Rev. A 2001, 64, 63808.
- de Oliveira, M.C.A.; de Sousa, F.W.S., Jr.; Santos, F.A.; Abeg, L.M.G.; Alencar, M.A.R.C.; Rodrigues, J.J., Jr.; de Oliveiraa, H.P. Dye-doped electrospun fibers for use as random laser generator: The influence of spot size and scatter concentration. Opt. Mater. 2020, 101, 109722.
- Consoli, A.; Lopez, C. Emission regimes of random lasers with spatially localized feedback. Opt. Express 2016, 24, 10912–10920.
- Redding, B.; Choma, M.A.; Cao, H. Spatial coherence of random laser emission. Opt. Lett. 2011, 36, 3404.
- Oliveira, N.T.C.; Vieira, A.M.; Araújo, C.B.D.; Martins, W.S.; Oliveira, R.A.D.; Reyna, A.S. Light Disorder as a Degree of Randomness to Improve the Performance of Random Lasers. Phys. Rev. Appl. 2021, 15, 064062.
- Vieira, A.M.; Oliveira, N.T.C.; De Araújo, C.B.; Martins, W.S.; De Oliveira, R.A.; Reyna, A.S. Influence of the Excitation Light Disorder on the Spatial Coherence in the Stimulated Raman Scattering and Random Lasing Coupled Regime. J. Phys. Chem. C 2021, 125, 5919.
- Leonetti, M.; Conti, C.; Lopez, C. The mode-locking transition of random lasers. Nat. Photonics 2011, 5, 615–617.
- Leonetti, M.; Conti, C.; López, C. Random laser tailored by directional stimulated emission. Phys. Rev. A At. Mol. Opt. Phys. 2012, 85, 43841.
- Kumar, B.; Homri, R.; Priyanka.; Maurya, S.K.; Lebental, M.; Sebbah, P. Localized modes revealed in random lasers. Optica 2021, 8, 1033.
- Li, Y.; Xie, K.; Zhang, X.; Hu, Z.; Ma, J.; Chen, X.; Zhang, J.; Liu, Z.; Chen, D. Coherent Random Lasing Realized in Polymer Vesicles. Photonic Sens. 2020, 10, 254–264.
- Ismail, W.Z.W.; Kamil, W.M.W.A.; Dawes, J.M. Enhancement of Random Laser Properties on Solid Polymer Films by Increasing Scattering Effect. J. Russ. Laser Res. 2019, 40, 364–369.
- Kitur, J.; Zhu, G.; Bahoura, M.; Noginov, M.A. Dependence of the random laser behavior on the concentrations of dye and scatterers. J. Opt. 2010, 12, 24009.
- Tommasi, F.; Ignesti, E.; Fini, L.; Martelli, F.; Cavalieri, S. Random laser based method for direct measurement of scattering properties. Opt. Express 2018, 26, 27615–27627.
- Noginov, M.A.; Zhu, G.; Frantz, A.A.; Novak, J.; Williams, S.N.; Fowlkes, I. Dependence of NdSc3(BO3)4 random laser parameters on particle size. J. Opt. Soc. Am. B 2004, 21, 191.
- Okamoto, T.; Adachi, S. Effect of particle size and shape on nonresonant random laser action of dye-doped polymer random media. Opt. Rev. 2010, 17, 300–304.
- Gummaluri, V.S.; Nair, R.V.; Vijayan, C. Random lasing from a colloidal gain medium with urchin-like TiO2 structures. In Proceedings of the SPIE 9920, the Active Photonic Materials VIII, San Diego, CA, USA, 16 September 2016.
- Ning, S.; Dai, K.; Zhang, N.; Zhang, Y.; Wu, Y.; Huang, J.; Xue, T.; Zhang, F. Improving the random lasing performance using nanocubes-silver film hybrid structure. J. Lumin. 2021, 231, 117788.
- Fan, S.; Zhang, X.; Wang, Q.; Zhang, C.; Wang, Z.; Lan, R. Inflection point of the spectral shifts of the random lasing in dye solution with TiO2 nanoscatterers. J. Phys. Appl. Phys. 2009, 42, 15105.
- Fan, S.; Zhang, X.; Wang, Q.; Zhang, C.; Wang, Z. Inflection point of the spectral shifts of the random lasing in dye solution showing transformation to weak localization. In Proceedings of the SPIE 7201, Laser Applications in Microelectronic and Optoelectronic Manufacturing VII, San Jose, CA, USA, 24 February 2009.
- Yi, J.; Feng, G.; Yang, L.; Yao, K.; Yang, C.; Song, Y.; Zhou, S. Behaviors of the Rh6G random laser comprising solvents and scatterers with different refractive indices. Opt. Commun. 2012, 285, 5276–5282.
- Meng, X.; Fujita, K.; Murai, S.; Konishi, J.; Mano, M.; Tanaka, K. Random lasing in ballistic and diffusive regimes for macroporous silica-based systems with tunable scattering strength. Opt. Express 2010, 18, 12153.
- Dey, A.; Pramanik, A.; Kumbhakar, P.; Biswas, S.; Pal, S.K.; Ghosh, S.K.; Kumbhakar, P. Manoeuvring a natural scatterer system in random lasing action and a demonstration of speckle free imaging. OSA Contin. 2021, 4, 1712.
- Bian, Y.; Shi, X.; Hu, M.; Wang, Z. A ring-shaped random laser in momentum space. Nanoscale 2020, 12, 3166–3173.
- Shi, X.; Ge, K.; Tong, J.H.; Zhai, T. Low-cost biosensors based on a plasmonic random laser on fiber facet. Opt. Express 2020, 28, 12233.
- Ye, L.; Feng, Y.; Lu, C.; Hu, G.; Cui, Y. Coherent random lasing from liquid waveguide gain layer containing silica nanoparticles. Laser Phys. Lett. 2016, 13, 105002.
- Shi, X.; Chang, Q.; Tong, J.; Feng, Y.; Wang, Z.; Liu, D. Temporal profiles for measuring threshold of random lasers pumped by ns pulses. Sci. Rep. 2017, 7, 5325.
- Uppu, R.; Mujumdar, S. Lévy exponents as universal identifiers of threshold and criticality in random lasers. Phys. Rev. A At. Mol. Opt. Phys. 2014, 90, 25801.
- Lepri, S.; Cavalieri, S.; Oppo, G.L.; Wiersma, D.S. Statistical regimes of random laser fluctuations. Phys. Rev. A At. Mol. Opt. Phys. 2007, 75, 63820.
- Lippi, G.L.; Wang, T.; Puccioni, G.P. Phase Transitions in small systems: Why standard threshold definitions fail for nanolasers. Chaos Solitons Fractals 2022, 157, 111850.
- Ghofraniha, N.; Viola, I.; Di Maria, F.; Barbarella, G.; Gigli, G.; Leuzzi, L.; Conti, C. Experimental evidence of replica symmetry breaking in random lasers. Nat. Commun. 2015, 6, 6058.
- Conti, C.; DelRe, E. Photonics and the Nobel Prize in Physics. Nat. Photonics 2022, 16, 6–7.
- Dai, G.; Wang, L.; Deng, L. Flexible random laser from dye doped stretchable polymer film containing nematic liquid crystal. Opt. Mater. Express 2020, 10, 68.
- Haddawi, S.F.; Humud, H.R.; Hamidi, S.M. Signature of plasmonic nanoparticles in multi-wavelength low power random lasing. Opt. Laser Technol. 2020, 121, 105770.
- Ismail, W.Z.W.; Dawes, J.M. Synthesis and Characterization of Silver-Gold Bimetallic Nanoparticles for Random Lasing. Nanomaterials 2022, 12, 607.
- Wan, Y.; Wang, H.; Li, H.; Ye, R.; Zhang, X.; Lyu, J.; Cai, Y. Low-threshold random lasers enhanced by titanium nitride nanoparticles suspended randomly in gain solutions. Opt. Express 2022, 30, 8222.
- He, J.; Chan, W.k.E.; Cheng, X.; Tse, M.l.V.; Lu, C.; Wai, P.K.A.; Savovic, S.; Tam, H.Y. Experimental and Theoretical Investigation of the Polymer Optical Fiber Random Laser with Resonant Feedback. Adv. Opt. Mater. 2018, 6, 1701187.
- Chen, Y.C.; Tan, X.; Sun, Q.; Chen, Q.; Wang, W.; Fan, X. Laser-emission imaging of nuclear biomarkers for high-contrast cancer screening and immunodiagnosis. Nat. Biomed. Eng. 2017, 1, 724–735.
- Pramanik, A.; Biswas, S.; Kumbhakar, P.; Kumbhakar, P. External feedback assisted reduction of the lasing threshold of a continuous wave random laser in a dye doped polymer film and demonstration of speckle free imaging. J. Lumin. 2021, 230, 117720.
- Chen, Y.C.; Chen, Q.; Tan, X.; Chen, G.; Bergin, I.; Aslam, M.N.; Fan, X. Chromatin laser imaging reveals abnormal nuclear changes for early cancer detection. Biomed. Opt. Express 2019, 10, 838.
- Chen, Y.C.; Chen, Q.; Wu, X.; Tan, X.; Wang, J.; Fan, X. A robust tissue laser platform for analysis of formalin-fixed paraffin-embedded biopsies. Lab Chip 2018, 18, 1057–1065.
- Chen, Y.C.; Chen, Q.; Zhang, T.; Wang, W.; Fan, X. Versatile tissue lasers based on high-Q Fabry-Pérot microcavities. Lab Chip 2017, 17, 538–548.
- Wang, W.; Zhou, C.; Zhang, T.; Chen, J.; Liu, S.; Fan, X. Optofluidic laser array based on stable high-Q Fabry-Pérot microcavities. Lab Chip 2015, 15, 3862.
- Xu, Z.; Tong, J.; Shi, X.; Deng, J.; Zhai, T. Tailoring whispering gallery lasing and random lasing in a compound cavity. Polymers 2020, 12, 656.
- Karl, M.; Dietrich, C.P.; Schubert, M.; Samuel, I.D.; Turnbull, G.A.; Gather, M.C. Single cell induced optical confinement in biological lasers. J. Phys. D Appl. Phys. 2017, 50, 84005.
- Ignesti, E.; Tommasi, F.; Fini, L.; Martelli, F.; Azzali, N.; Cavalieri, S. A new class of optical sensors: A random laser based device. Sci. Rep. 2016, 6, 35225.
- Zehentbauer, F.M.; Moretto, C.; Stephen, R.; Thevar, T.; Gilchrist, J.R.; Pokrajac, D.; Richard, K.L.; Kiefer, J. Fluorescence spectroscopy of Rhodamine 6G: Concentration and solvent effects. Spectrochim. Acta Part A Mol. Biomol. 2014, 121, 147–151.
- Bavali, A.; Parvin, P.; Mortazavi, S.Z.; Mohammadian, M.; Mousavi Pour, M.R.; Pour, M.R.M. Red / blue spectral shifts of laser-induced fluorescence emission due to different nanoparticle suspensions in various dye solutions. Appl. Opt. 2014, 53, 5398–5409.
- Hohmann, M.; Späth, M.; Ni, D.; Dörner, D.; Lengenfelder, B.; Klämpfl, F.; Schmidt, M. Random laser as a potential tool for the determination of the scattering coefficient. Biomed. Opt. Express 2021, 12, 5439.
- Dominguez, C.T.; Maltez, R.L.; dos Reis, R.M.S.; de Melo, L.S.A.; de Araújo, C.B.; Gomes, A.S.L. Dependence of random laser emission on silver nanoparticle density in PMMA films containing rhodamine 6G. J. Opt. Soc. Am. B 2011, 28, 1118.
- Beckering, G.; Zilker, S.J.; Haarer, D. Spectral measurements of the emission from highly scattering gain media. Opt. Lett. 1997, 22, 1427.
- Ta, V.D.; Caixeiro, S.; Saxena, D.; Sapienza, R. Biocompatible Polymer and Protein Microspheres with Inverse Photonic Glass Structure for Random Micro-Biolasers. Adv. Photonics Res. 2021, 2, 2100036.
- Zhou, H.; Feng, G.; Yao, K.; Yang, C.; Yi, J.; Zhou, S. Fiber-based tunable microcavity fluidic dye laser. Opt. Lett. 2013, 38, 3604.
- El-Dardiry, R.G.; Lagendijk, A. Tuning random lasers by engineered absorption. Appl. Phys. Lett. 2011, 98, 161106.
- Zhang, W.; Cue, N.; Yoo, K.M. Emission linewidth of laser action in random gain media. Opt. Lett. 1995, 20, 961.
- Papadakis, V.M.; Stassinopoulos, A.; Anglos, D.; Anastasiadis, S.H.; Giannelis, E.P.; Papazoglou, D.G. Single-shot temporal coherence measurements of random lasing media. J. Opt. Soc. Am. B 2007, 24, 31.
- Ismail, W.Z.W.; Liu, D.; Clement, S.; Coutts, D.W.; Goldys, E.M.; Dawes, J.M. Spectral and coherence signatures of threshold in random lasers. J. Opt. 2014, 16, 105008.
- Noginov, M.A.; Egarievwe, S.U.; Noginova, N.; Caulfield, H.J.; Wang, J.C. Interferometric studies of coherence in a powder laser. Opt. Mater. 1999, 12, 127–134.
- Cao, H.; Xu, J.Y.; Ling, Y.; Burin, A.L.; Seeling, E.W.; Liu, X.; Chang, R.P. Random lasers with coherent feedback. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 111–119.
- Letokhov, V. Generation of Light by a Scattering Medium with Negative Resonance Absorption. Sov. J. Exp. Theor. Phys. 1968, 26, 835.
- Wiersma, D.S. The physics and applications of random lasers. Nat. Phys. 2008, 4, 359.
- Yin, L.; Liang, Y.; Yu, B.; Wu, Y.; Ma, J.; Xie, K.; Zhang, W.; Zou, G.; Hu, Z.; Zhang, Q. Quantitative analysis of “Δl = ls - lg” to coherent random lasing in solution systems with a series of solvents ordered by refractive index. RSC Adv. 2016, 6, 98066–98070.
- Cao, M.; Zhang, Y.; Song, X.; Che, Y.; Zhang, H.; Dai, H.; Zhang, G.; Yao, J. Random lasing in a colloidal quantum dot-doped disordered polymer. Opt. Express 2016, 24, 9325.
- Jiang, X.; Feng, S.; Soukoulis, C.M.; Zi, J.; Joannopoulos, J.D.; Cao, H. Coupling, competition, and stability of modes in random lasers. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 104202.
- Jiang, X.; Cao, H.; Ling, Y.; Xu, J.Y.; Soukoulis, C.M. Mode repulsion and mode coupling in random lasers. Phys. Rev. B Condens. Matter Mater. Phys. 2003, 67, 161101(R).
- Lin, S.; Wang, Z.; Li, J.; Chen, S.; Rao, Y.; Peng, G.; Gomes, A.S. Nonlinear dynamics of four-wave mixing, cascaded stimulated Raman scattering and self Q-switching in a common-cavity ytterbium/raman random fiber laser. Opt. Laser Technol. 2021, 134, 106613.
- Vanneste, C.; Sebbah, P. Selective Excitation of Localized Modes in Active Random Media. Phys. Rev. Lett. 2001, 87, 183903.
- Wiersma, D.S.; Bartolini, P.; Lagendijk, A.; Righini, R. Localization of light in a disordered medium. Nature 1997, 390, 671–673.
- Sapienza, R. Determining random lasing action. Nat. Rev. Phys. 2019, 1, 690–695.
- Wiersma, D.S.; Lagendijk, A. Light diffusion with gain and random lasers. Phys. Rev. E 1996, 54, 4256–4265.
- Mujumdar, S.; Ricci, M.; Torre, R.; Wiersma, D.S. Amplified extended modes in random lasers. Phys. Rev. Lett. 2004, 93, 53903.
- Yamilov, A.; Wu, X.H.; Cao, H.; Burin, A.L. Absorption induced confinement of lasing modes in diffusive random medium. Opt. Lett. 2005, 30, 2430.
- Apalkov, V.M.; Raikh, M.E.; Shapiro, B. Random resonators and prelocalized modes in disordered dielectric films. Phys. Rev. Lett. 2002, 89, 16802.
- Raikh, M.E.; Apalkov, V.M.; Shapiro, B.; Polson, R.C.; Vardeny, Z.V. Coherent random lasing: Trapping of light by the disorder. Proceedings of SPIE 5472, Noise and Information in Nanoelectronics, Sensors, and Standards II, Maspalomas, Gran Canaria Island, Spain, 25 May 2004.
- Wu, X.; Fang, W.; Yamilov, A.; Chabanov, A.A.; Asatryan, A.A.; Botten, L.C.; Cao, H. Random lasing in weakly scattering systems. Phys. Rev. A 2006, 74, 53812.
- Wu, X.; Cao, H. Statistics of random lasing modes in weakly scattering systems. Opt. Lett. 2007, 32, 3089.
- Vanneste, C.; Sebbah, P.; Cao, H. Lasing with resonant feedback in weakly scattering random systems. Phys. Rev. Lett. 2007, 98, 143902.
- Polson, R.C.; Raikh, M.E.; Valy Vardeny, Z. Universality in unintentional laser resonators in π-conjugated polymer films. C. R. Phys. 2002, 3, 509–521.
- Polson, R.C.; Raikh, M.E.; Vardeny, Z.V. Universal properties of random lasers. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 120–123.
- Cao, H.; Ling, Y.; Xu, J.Y.; Burin, A.L. Probing localized states with spectrally resolved speckle techniques. Phys. Rev. E Stat. Phys. Plasmas Fluids Related Interdiscip. Top. 2002, 66, 25601.
- Cao, H. Review on latest developments in random lasers with coherent feedback. J. Phys. Math. Gen. 2005, 38, 10497–10535.
- Polson, R.C.; Vardeny, Z.V. Organic random lasers in the weak-scattering regime. Phys. Rev. B 2005, 71, 45205.
More
