The design and operation of wastewater treatment plants must consider quite a few uncertain factors, such as the physical and chemical composition of wastewater and the biological composition of organisms used to treat the wastewater. There are increasing concerns about the environmental impacts of wastewater, in terms of safe treatment, safe disposal, and safe reuse ^[1][2][3][1,2,3]. Over the years, this has led to Artificial Intelligence techniques, predominantly nature-inspired Artificial Intelligence techniques, being used for process control within treatment plants to maximize the efficiency of treatment and decrease energy consumption [4].

The most common type of biological wastewater treatment is the activated sludge process (ASP). Activated sludge is a mix of wastewater that contains a population of bacteria that focus on removing biological nitrogen, biological phosphorous, and organic carbon substances from the wastewater [5]. A basic process diagram for ASP is shown in Figure 1.

2. Modelling of Activated Sludge Process

A typical model that would simulate the ASP operation will have the following steps: a model objective, data collection, mathematical equations or models for each ASP as mentioned above, model calibration, and model validation [6]. Mathematical modelling has become an integral part of the design and operation of wastewater treatment processes, particularly the ASP. Simulations conducted with the models created have been a great source of value for ASP operators, designers, and even the wider scientific community. The main benefits of these models are the wide range of system functions and conditions that can be simulated and tested and solutions that can be found in a short time with low associated costs [7]. There are three main types of modelling that have been historically used for the ASP: deterministic or mechanistic modelling, stochastic modelling, and hybrid models combining the two approaches. The most efficient models use hybrid models where stochastic modelling is used for the hard-to-define parameters and variables in the treatment process. Deterministic modelling is used for the parts of the process that are both better understood and can be validated using the biological, physical, and chemical laws of the ASP [8]. Historically, deterministic models were the earliest type of work on activated sludge plants. Experimental data were taken and used to generate mathematical equations that depicted the relationship between variables in the various stages of the ASP. The most used mathematical model of the ASP was created by the International Association on Water Pollution Research and Control (IAWPRC) Task Group [9]—the Activated Sludge Model No. 1 (ASM1). Even though it was developed in 1987, researchers still widely use it for their work, albeit with modified versions. The main processes involved in the traditional ASM1 model were the microorganisms’ growth, maintenance, and decay. Nitrification and denitrification were also included in some models along the way. It was accepted that this simplified approach has some demerits due to considering only these few processes and components [8]. Over the years, many modifications have been made to the traditional model approach. For example, Eckhoff et al. [10] used COD instead of BOD as a parameter to calculate the inert fraction of the substrate. Models based on COD are generally preferred over BOD in academic/research models because they are better at conserving the mass oxygen balance. However, BOD models are used to better characterize influent wastewater [11]. There are a few drawbacks to the ASM1 model. The International Water Association (IWA) has only given reference values for the dynamic or stoichiometric parameters of the model and its application to a real-life WWTP (real/ideal treatment plant); the parameters will have to be corrected [12]. Different calibration data sets can produce the same results. Some variables used cannot be measured in the real-time process, making it hard to verify the model. Certain factors are not considered, such as the dependency of temperature and pH on the constants used. Calibration and model verification can be difficult and highly sensitive—sometimes, extensive lab equipment is required. Phosphorous removal was also not considered in this model, which created issues in practical application [13]. In 1995, a modified version of the ASM1 called the Activated Sludge Model No. 2 (ASM2) was developed, which included phosphorous removal in addition to carbonaceous and nitrogenous material. However, phosphorous removal is complex, thereby complicating the calibration and verification of the ASM2 model. The ASM1 and ASM2 were further improved by creating two models, Activated Sludge Model No. 2d (ASM2d) and Activated Sludge Model No. 3 (ASM3). ASM2d builds upon ASM2 by adding denitrifying activity of Polysulphate Accumulating Organisms that show better relation between phosphorous and nitrate. ASM3 was developed similar to ASM1 but considering the effect of storage polymers in heterotrophic activated sludge conversion [14]. To summarize, ASM1 can be used to simulate both carbon removal and denitrification, ASM2 simulates phosphorous removal in addition to decarbonization and denitrification, ASM2d further improved the relationship between phosphorous and nitrate in ASM2, and ASM3 improved upon ASM1 adding the effect of storage polymers. All the ASM models are mechanistic models where differential equations are used to describe and restore the dynamic changes in the wastewater treatment system. The models ASM1 and ASM2, ASM2d use the theoretical basis of death–regeneration and maintenance, whereas ASM3 utilizes the theoretical basis of endogenous microbial respiration [13]. Due to the many processes, variables, and parameters involved, activated sludge models are often validated and calibrated by trial and error with no standard procedure ^[8][15][8,15]. For example, Siegrist and Tschui [16] created several models with different sets of parameters for partial and sequential calibration. Calibration for COD removal was undertaken by considering the oxygen consumption rate when other parameters were held constant. The model was validated by comparing it with full-scale treatment plant data, where an example would be [17]. They created a dynamic model for carbon and nitrogen removal and validated it with data obtained from 10 days of monitoring Norwich Sewage Works in England. Côté et al. [18] used a hybrid model, which improved upon previous work by using a neural network to predict and reduce error in mechanistic model variables such as effluent suspended solids, effluent COD, and volatile solids in return sludge, etc. The mechanistic model was validated with data from Norwich Sewage Works.

2.1. Artificial Intelligence Used in Modelling of WWTP

The traditional mechanistic models, such as ASM1, have reached a limit when considering the complexity and accuracy of application to the ASP, with some of the issues mentioned in Section 2. Thus, Artificial Intelligence can be used as a modelling tool to minimize the complexities and reduce computing time [19]. There are several different types of AI modelling tools adapted for different fields and functions. Of these are feedforward Artificial Neural Networks (ANNs); radial basis functions (RBFs); recurrent neural networks (RNNs); multilayer perceptron (MLP) using backpropagation learning; hybrid models such as adaptive neuro-fuzzy inference (ANFIS). More recently, deep neural networks (DNNs) contain multiple hidden layers and require significant computational power ^[20][21][20,21]. The traditional ANN has a few limitations such as poor generalization due to incorrectly chosen network structure, hard-to-interpret system information stored in neuron weights, and a large amount of data required for accuracy. ANFIS tends to overcome a few of these limitations [21]. Additionally, Feedforward Artificial Neural Networks (FANNs)—MLPs and RBFs—are commonly used in wastewater treatment operations. MLPs have been found to be better than regression models for wastewater treatment [8], whilst RBFs are useful because they can easily predict system behavior from past observations [22]. DNNs vary from typical feedforward neural networks (ANNs) because DNNs contain more neurons, complexity in connecting layers, more computing power required to train the network due to having more neurons/connections, and automatic feature extraction [22]. Some of these tools, along with applications in wastewater treatment, particularly the ASP, are discussed below.

2.2. Artificial Neural Network (ANN)

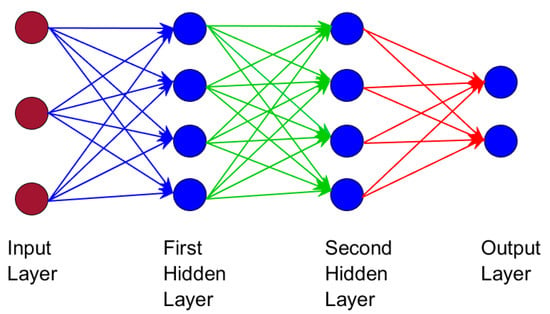
ANN is designed as a simplified version of the human brain, where inputted neurons generate output signals. The general structure of a neural network is shown in Figure 2, where there are layers of interconnected neurons. There are several layers: the input layer, where inputs are given as weights to input neurons; the output layer, where output neurons do processing based on the input using an activation function and generate output; and single/multiple hidden layers, where intermediary neurons process the weighted sums of the inputs. Sometimes, output neurons can also be connected to each other and not just to the previous inputs, but this is complex and uncommon ^[20][23][20,23]. The neuron weights are determined using multiple data sets’ training and validation processes. This is achieved by introducing various data sets of inputs and corresponding outputs (real experimental results) to the neural network. Weights will be continuously adjusted to minimize errors. These training data sets will also help identify the number of hidden neurons; more data points used means more hidden neurons are required. Validation or verification using separate datasets should be conducted at the end of the training process to ensure it was achieved correctly [23]. A few examples of ANN used in WWTP modelling are given below. Plonka [23] used a layered ANN to create a virtual sensor that measures nitrate–nitrogen in the activated sludge reactor tank. The predicted readings from the ANN were then compared to the actual probe in the reactor. Cascade training was used to form a layered ANN wherein more neurons are added, each creating another network layer. There has not been an exact method of calculating the size of an ANN, so this type of training is beneficial. The training was conducted using ‘FannTool’ graphical interface [23]. ANNs require large samples of inputs and outputs to train the network, in this case, the measuring probes. The input needed was obtained by computer simulation via the STOAT (Sewage Treatment Operation and Analysis over Time) application with the BSM1 (Benchmark Simulation Model No. 1) mathematical model. STOAT works with both COD and BOD measurements. The ANN was run with two sets of data—one obtained from the simulation and another set of distorted data where artificial random noise of ±2% of each individual value was introduced into the simulation data. Values of average error found for both sets of data were found to be well below the sensitivity of the actual measuring probes. The distortion had a negligible effect on the accuracy of the calculations. Messaoud et al. [24] used a standard feedforward neural network to predict the performance of the wastewater treatment process. The ANN used had one hidden layer and one output layer, with training conducted for a different number of iterations and a number of hidden layer neurons. Training and validation were conducted with different data sets taken from a WWTP in Ain Beida, Algeria, designed for 16,000 m³/day flow and 300,000 equivalent population. Sensitivity analysis was conducted to determine input parameters. Results showed the ANN model is a good tool for reliability prediction and can help plant operators predict parameters, especially BOD, which usually has a five-day determination period.

2.3. Multilayer Perceptron Neural Network (MLP)

MLPs are a class of feedforward ANNs, especially with backpropagation (MLPBPNN) which minimizes the error function of MLP by using a gradient descent method to change the value of the weights. Kusiak and Wei [25] used a multilayer perceptron (MLP) neural network to build and validate an ASP model. Data used were from an industrial Wastewater Reclamation Authority (WRA) in Des Moines, Iowa, US. Dissolved oxygen (DO) concentration was used as a control variable. The MLP neural network was used to build three prediction models for minimizing three parameters: airflow rate, effluent CBOD, and TSS concentration. Two hundred networks were trained for each model, each with one hidden layer and neurons between three and ten. All airflow rates and TSS rates were predicted accurately; however, CBOD values obviously differed. The correlation coefficient was 0.99, indicating an accurate model.

2.4. Adaptive-Network-Based Fuzzy Inference System (ANFIS)

ANFIS joins fuzzy logic and ANN to form a combined system that extracts fuzzy rules from data to a rule-base and feeds it to the ANN [21]. A few examples of ANFIS used in WWTP are summarized below. Araromi et al. [21] used an adaptive neuro-fuzzy inference system (ANFIS) for non-linear dynamic system identification of the wastewater treatment process. The study used ANFIS and GLM (Generalized Linear Model Regression). Brute force exhaustive search was used for the ANFIS model wherein all elements of the search space are tested iteratively, and LASSO (least absolute shrinkage and selection operator) was used as penalized regression method in GLM. Outliers were removed from the data and smoothed out. For both training and validation datasets, ANFIS predicted values better than GLM regression models. It was also found that ANFIS can be used to estimate the time required to reach an adequate performance level, as the model indicated that there are time lags in the treatment process. Rustum [8] used an improvised ANFIS using the Kohonen Self-Organizing Map (Hybrid KSOM-ANFIS) to model an ASP and predict effluent Biological Oxygen Demand (BOD₅) and Suspended Solids (SS) concentration. Results showed the hybrid model outperformed the ANFIS model in predicting the necessary values [8]. KSOM was used to extract features from noisy data and fill in missing values ^{[26][27][28][29]}[26,27,28,29]. Three years of data were taken from a WWTP in Edinburgh, UK, and two models were tested, one with ANFIS alone and another with the hybrid KSOM-ANFIS [27]. Du et al. also [30] used ANFIS to predict and have a heuristic understanding of sludge age in ASP. The combined fuzzy logic with the neural network was able to not only understand the complex relationships within the data, but also perform rule extraction. Additionally, Rustum and Forrest [31] developed a model for fault detection in the activated sludge process using the Kohonen self-organizing Map. Rustum and Adeloye [26] developed a model for knowledge discovery from activated sludge processes using unsupervised neural networks (Kohonen Self-Organizing Map).

2.5. Deep Learning Neural Network (DNN)

DNNs are a form of ANN where there is higher complexity in the number of layers and connections between layers. It is the latest development in the field of ANNs, and an example used in WWTP is given below. Oulebsir [32] used a deep neural network (DNN) to optimize the energy conservation of WWTP. It is estimated that energy costs consume 28% of the total costs of wastewater treatment. Daily data for entry/exit pollution parameters—[BOD5, COD, SS, NH4], total flow, total energy consumed, influent temperature, and recirculated sludge flow—were collected from the treatment plant and cleaned of missing data and outliers. Two types of data selection were performed; effluent quality values that were near design values corresponding to environmental standards were selected. Key performance indicators (KPIs) used here were Treatment Yield, Global Treatment Yield, and Standardized Global Treatment Yield. The second selection was made to find the best energy consumption according to certain KPIs: the Pollution Index, Abatement Degree of Pollution, Global Degree of Abatement of Pollution, and Water Quality Index. The selected data were then used to train (80% of data) and test (20% of data). Trial and error were used for the number of neurons/hidden layers. Results showed good performance for all models. A model trained with Global Degree of Abatement of Pollution (GPAB) selected data was best; however, Root Mean Squared Error observations standard deviation ratio (RSR) in the testing period, and Percentage Bias (PBIAS) values indicated overfitting. The model trained with Pollution Index PI (Water Quality Index, WQI) also had R² close to the GPAB model; however, PBIAS showed underfitting. It was concluded from the values of the KPIs that pollution entering the WWTP had more effect on energy consumption than effluent parameters and removal efficiency.