Additive manufacturing (AM) reduces the limitations in the fabrication of complex lattice structures. A variety of design tools are rapidly developed to facilitate the design of geometrically ccomplex structures and allow designers to realize complicated models. Weight, volume, and manufacturing cost reductions are some benefits of AM over conventional manufacturing [1][2][3][4]. Among the lattice structures, architected materials with topologies based on Triply Periodic Minimal Surfaces (TPMS) have attracted much attention due to their mathematically controlled topologies and their excellent physical and mechanical properties.

The TPMS is composed of infinite, non-self-intersecting, periodic surfaces in three principal directions. Schwarz discovered the first example of TPMS, wasnamed the Diamond minimal surface (Figure 1a), in 1865 [5]. Later, his student, Neovius, discovered the Neovius surface (Figure 1b) in 1883 [6]. They further discovered several minimal surfaces, e.g., the Primitive (Figure 1c). Almost a century later, in 1970, Schoen introduced various types of minimal surfaces, and the Gyroid minimal surface (Figure 1d) was the most famous [7]. The TPMS is characterized as a minimal surface besincause the curvature along the principal curvature planes is equal and opposite at every point, resulting in a zero mean curvature of zeroe.

Figure 1 Minimal surfaces (a) Diamond; (b) Neovius; (c) Primitive; (d) Gyroid.

The TPMS is composed of infinite, non-self-intersecting, periodic surfaces in three principal directions. Schwarz discovered the first example of TPMS was the Diamond minimal surface (Figure 1a) in 1865 [5]. Later, his student, Neovius, discovered the Neovius surface (Figure 1b) in 1883 [6]. They further discovered several minimal surfaces, e.g., the Primitive (Figure 1c). Almost a century later, in 1970, Schoen introduced various types of minimal surfaces, and the Gyroid minimal surface (Figure 1d) was the most famous [7]. The TPMS is characterized as a minimal surface because the curvature along the principal curvature planes is equal and opposite at every point, resulting in a mean curvature of zero.

where α, β, and γ denote constants related to the unit cell size (L) in x, y and z, respectively; c is the offset parameter, which equals zero for a single unit cell of the TPMS.

Twohe approachTPMS-based lattices can create the be constructed using two methods based on the minimal surfaces. The solid-based TPMS lattices based on the minimal surf, also known as the skeleton-based TPMS structure (Figure 2a), ces. Tan be created with the first approach that is achieved by considering the volume bound by the minimal surface to create the solid. The sheet-based TPMS lattice, also known as the skeleton-based TPMS structure (Figure 2ab). T is the second one is crethat is generated by offsetting the minimal surface along its normal direction to create a double surface. This surface is known as the sheet. With mathematical realized, the TPMS-based TPMS lattice (Figure 2b). Witstructures h thavese smooth curvatures, the TPMS-based structures, which can eliminate the stress concentrations commonly found in other structures.

Figure 2 Examples of solid- and sheet-based TPMS lattices.

2. TPMS-related investigations

2.1 Mechanical performances

To demonstrate the merits of the TPMS-based structures, the performances of the TPMS-based structures are analyzed and compar have been examined with other conventional structures. Among the performancThe majority of studies in differentvarious fields, most of the research has focused on have investigated mechanical performances. Speirs et al. [8] reported that due to TPMS-basedno nodal points in the TPMS structures acquired superior fatigue resistance compared to, they outperformed the octahedron unit owing to smooth surfaces without nodal pointsin terms of fatigue resistance. Khan et al. [9] demonstrated that in comparison to conventional lattice-frame materials, the sheet-IWP structures exhibitedgave superior viscoelastic behaviors under uniaxial loading than other lattice-frame materials. Wang et al. [10] presented that when compared to cubic and octet-strut-based designs, the sheet-Gyroid structure obtained the best stability and exhibipresented the widest rangevariety of mechanical properties compared to cubic and octet-strut-based structures. Teng et al. [11] reported that in the erms of stiffness, yield stress, and toughness, the sheet-Gyroid structure outperformed thbetter than the BCC and truss lattice structures in stiffness, yield stress, and toughness, as ss, as shown in Figure 3. Overall, the TPMS-based strulattices outperform strut-based structures provide betterin terms of mechanical performance than the strut-based structures. Thus. As a result, the TPMS-based structures, especially the sparticularly those based on sheet-based ones, can be employed in different used in a variety of disciplines requiring that demand high mechanical strength.

Figure 3 Normalized mechanical properties of the Gyroid, BCC, Truss and Primitive lattices with respect to the wall thickness, adapted from Teng et al. [11]

2.2 Mass transfer

The TPMS structures have interconnected curved walls with non-tortuous pores, which are appropriatre suitable for mass transfer and permeability appplications. From the flow perspective, previous studies have focused on permeability and wall shear stress. Still, the flow considered in these investigations was mainly achieved in the Darcy regime, and the non-linear inertial effects were negligible because they have continuously curved walls and non-tortuous pores. Ali et al. [12] reported that the sheet-Gyroid structure shprovided cowed mparable fluid permeability but higher wall shear stress than the lattice-based models in the same porosity but generated comparable fluid permeability. Montazerian et al. [13] studied cylindrical ducts of different lattice- and TPMS-based scaffolds. They showed that the TPMS-based scaffolds, especially the solisolid-IWP structure, were was more permeable than different lattice-based onemodels in the longitudinal fluid flow direction, as presented in Figure 4. Also, the TPMS-based scaffolds within a wide range of porosity exhibited high, the TPMS-based scaffolds showed larger normalized permeability values than the fiber-based structuremodels [14]. Even Although the porosity of the fiber-based structure iermeability increased the permeabiliwith the porosity, the tortuosity was significant of the fiber-based structure dramatically decreased [15], which h negatively affected thead a detrimental effect on fluid mixing and heat transfer performance.

Figure 4 Normalized longitudinal permeability versus porosity for different lattices, adapted from Montazerian et al. [13].

2.3 Thermal conductivity

Many designers Thave tested the thee thermal conductivity of different TPMS-based structureses has been tested by many designers. According to the experimental resultinvestigations by Wang et al. [16], the sheet-FRD structures achieved 103% higher thermal conductivity than thcompared to the commercial stochastic foams with the same porosity. T, the sheet-TPMSFRD structures also provide bettechieved 103% higher thermal conductivity than the fiber-based structure since . It has been also observed by Ni et al. [17] that the normalized thermal conductivity values of the fiber-based porous media considerably varied with the fiber direction; [17].hence, Tthe main reason for the highsheet-based TPMS structures can also provide better thermal conductivity ithan the sheet-TPMSfiber-based models. The connection of the curved wall in the TPMS-based structures was the main factor in excellent connectivity of the interconnected curvaturethermal conductivity.

Also, it has been reported that theff TPMS topologies have a significant impact on effective thermal conductivity strongly depends on the topologies. Qureshi et al. [18] presented that the sheet-Primitive structure exhibited the highest value, followed by sheet-IWP and sheet-Gyroid structures, whereasile the Kevin cell model caused the lowest value. Smith et al. [19] concluded that the thermal conductivity of the TPMS-based slattructurices was inversely proportional to the surface area-to-volume ratio. However, the thermal performance of cooling channels was typically proportional to surface areas for convective heat transfer. Overall, the thermal conductivity for most sheet-TPMS structures is similar, significantly higher than conventionallyn stochastic metal foams and lattice-frame materials, as shown in Figure 5.

Figure 5 Normalized thermal conductivity for different lattices, adapted from Kaur and Singh [2]. Octet [20], Rhombi-Octet [21], Solid-Gyroid [22], Solid-Primitive [22], Sheet-CLP [22], Sheet-Neovius [22], Sheet-Fischer Koch S [22], Stochastic metal foam (Al) [23], Stochastic metal foam (FeCrAl) [24].

2.4 Forced convective heat transfer

UnlikThe conventional pin-shaTPMS-equipped heat sinks, the heat sinks with TPMS structures ha have a more complex geometry, forc than typical pin-shaped heat sinks, causing the fluid to change trajectory as it flows pastpasses the heated areasection [25][26]. The large surface area per unit volume, smooth curved wall, and complexicated topology qualifyof the TPMS-based structures to be examined asare preferable for high-performance heat sinks. Moreover, being mathematically realized, the the complexity level of the TPMS-based heat sinks can be controlled to optimizenhance thermal performance.

To sincompare the heat transfer performance of TPMS-based structures, te they are mathematically realized.

The globally averaged Nusselt number (Nu) of the TPMS-based structures and different cooling geometries, including are plotted in Figure 6 to dicomplesare [27],the ribs [28], lheat ticework structuresransfer performance. [29],It pin finss evident [21],that aind micro-lattice structures comparison to the [21], is plotthed inr cooling Figure 6. Igeomet ris evident that es, the TPMS-based structures showexhibit higher globally averaged Nusselt numbers, especialparticularly for the solid-Diamond and solid-Gyroid structures than the other cooling geometriese. At the Reynolds number (Re) of 8000, the globally averaged Nusselt numberalue for the solid-Diamond structure is hmuch higher than the pin fins, BCC, Octa, Kagome and X-type micro-lattices by about 73%, 35%, 98%, 53% and 25%, respectively. Among the TPMS-based st structures, t. The sheet-Gyroid structure shows lowcauses the lowest values of the globally averaged Nusselt numbers. On average, tamong the TPMS-based lattices. The solid-Diamond and solid-Gyroid structures outperform the sheet-Gyroid structure by lattices, on average, perform 1.27 and 1.23 times. This increase is due to the higher surface area intersecting the flow field better than the sheet-Gyroid structure. However, it has been observed that the sheet-Gyroid structure outperformedshows higher values than the solid-Gyroid structure at Re > 6800, attributeddue to the enhancedstrong fluid mixing in the sheet-Gyroid structure.

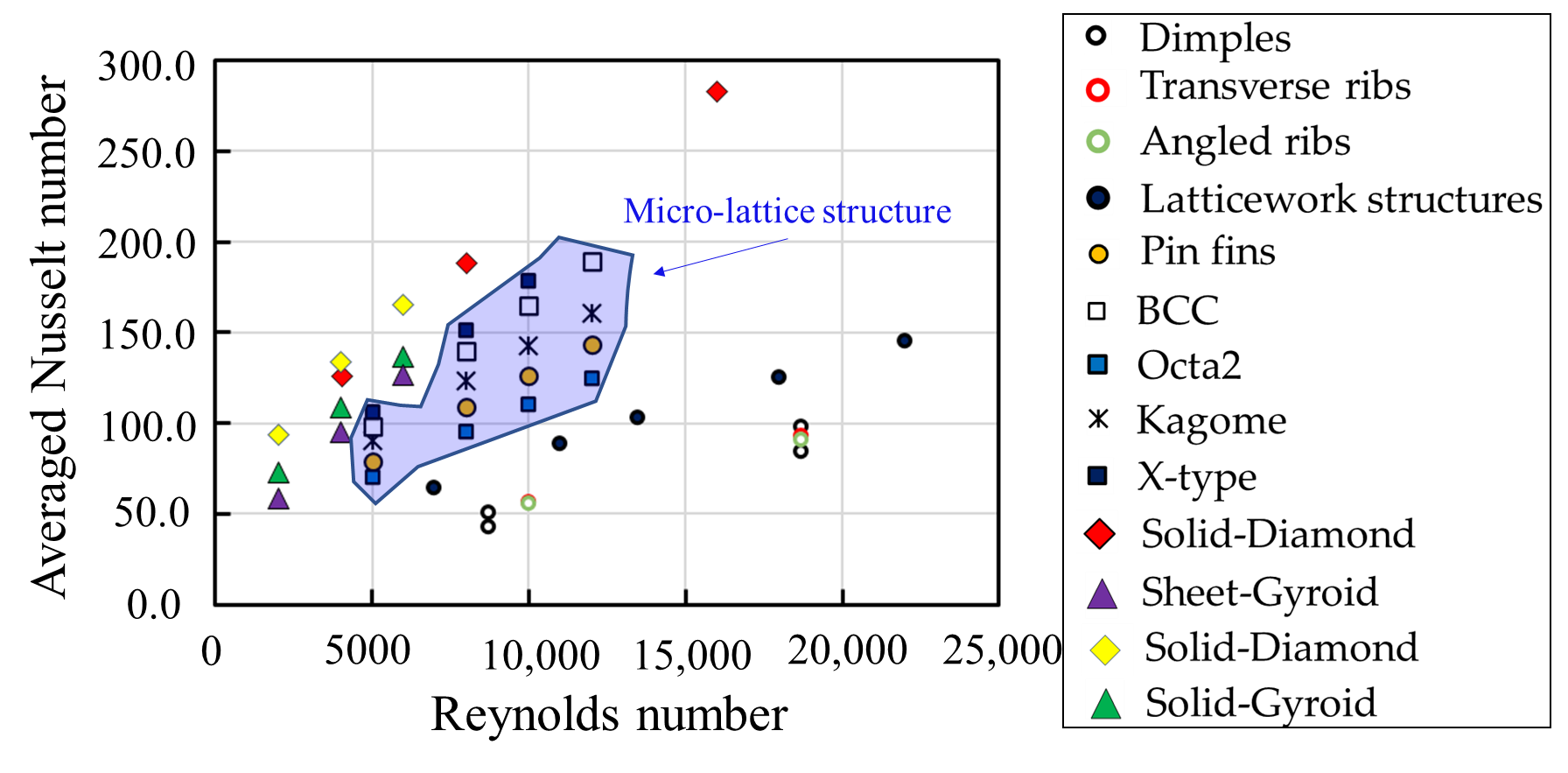
Figure 6 Comparisons of globally averaged Nusselt number of the TPMS structures with other cooling strategies. Dimples [27], Transverse ribs [28], Angled ribs [28], Latticework structures [29], Pin fins [21], BCC [21], Octa lattices [21], Kagome lattices [21], X-type lattices [21], Solid-Diamond structures [30][31], Sheet-Gyroid structures [31], Solid-Diamond structures [31], Solid-Gyroid structures [31].

The globally averaged Nusselt number ratio wplotted agaithnst friction factor ratios for different geometries are plottedis shown in Figure 7 to compare the relative thermal performance of the cooling structurese. The results show that twith friction factor ratios between 55.0 and 75.0, the solid-Diamond structure acquirhieves the highest Nusselt number ratio, up to 8.0–10.0, with friction factor ratios between 55.0–75.0. T-10.0. In comparison to the solid-Diamond structure, the solid- Gyroid structure causeexhibits lower Nusselt number ratios to the solid-diamond structure with similar with comparable friction factor ratios. TCompared to micro-lattice structures, the sheet-Gyroid structure generatproduces higher Nusselt number ratios than the micro-lattice structures but causes highand greater friction factor ratios. The ribs and dimples produce minor friction factor ratios. Meanwhile, the dimples and ribs give between 1.2 and 3.0 while providing the lowest Nusselt number ratios of about 1.5–2.0 while producing minor friction factor ratios between 1.2–3, which range from 1.5 to 2.0.

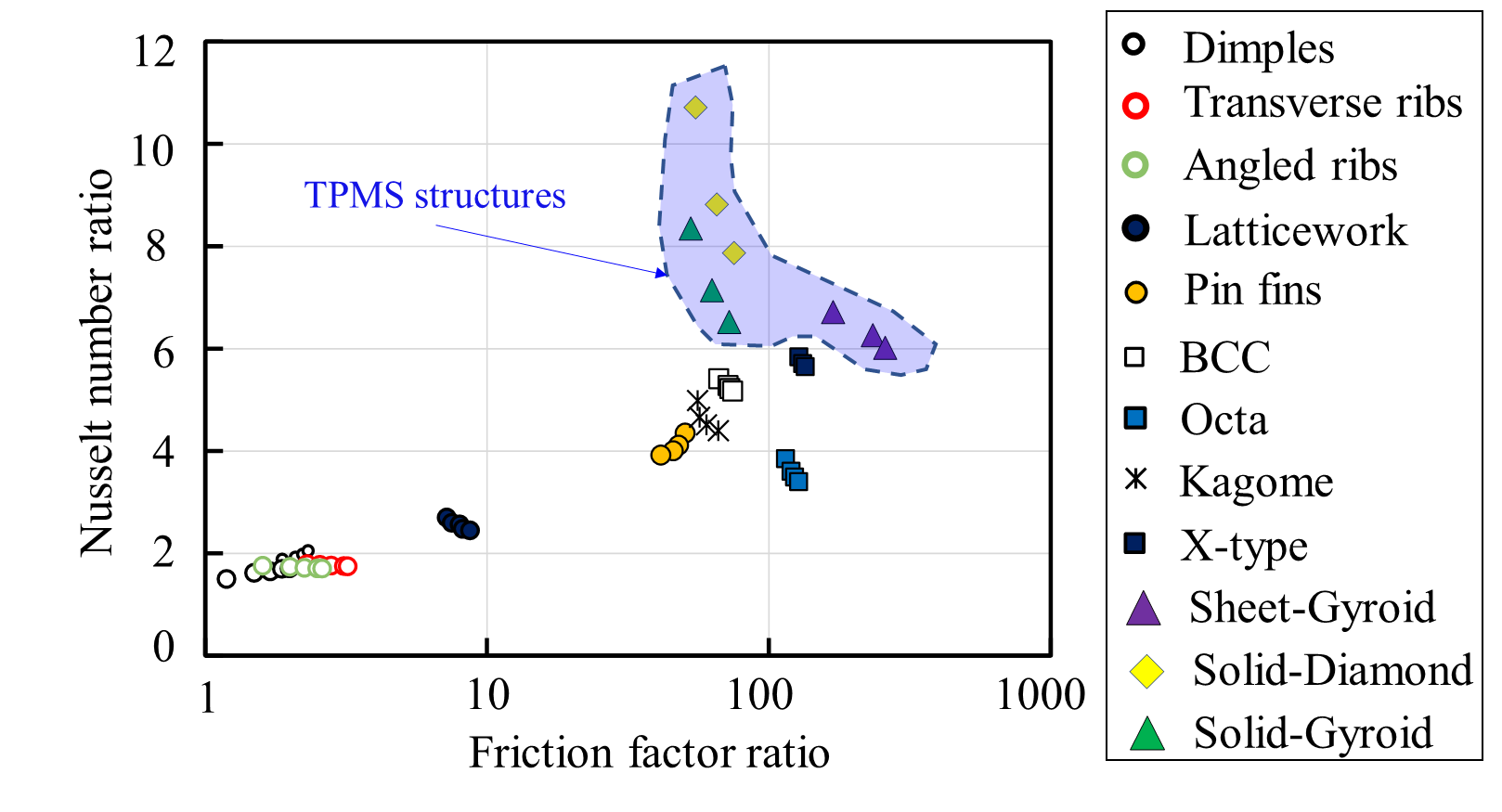
Figure 7 Relative thermal performance for different cooling structures. Dimples [27], Transverse ribs [28], Angled ribs [28], Latticework structures [29], Pin fins [21], BCC [21], Octa lattices [21], Kagome lattices [21], X-type lattices [21], Solid-Diamond structures [31], Sheet-Gyroid structures [31], Solid-Diamond structures [31], Solid-Gyroid structures [31].

2.5 Other applications

TheIn TPMS-based structures are being examined as spacers in the order to improve heat and mass transfer in membrane distillation to enhance heat and mass transfer, the TPMS-based structures are being investigated as spacers [32][33]. It was found that compared to commercial spacers, the TPMS-based spacers enhancincreased the overall film heat transfer coefficient by 60% compared to the commercial spacersup to 60%.

The larger surface area is essential for larger chemical reactions in catalytic sup-ports, fuel cells, ports and battery applications. Abu Al-Rub and Al-Ketan [34] proposed using TPMS-based structures as catalytic substrates. Al-Ketan et al. [35] examinnalyzed the flow propertiecharacteristics of the solid- and sheet-TPMS-based substrates and founrevealed that the CLP-based substrate exhibited a well-reduced topology showed a much lower pressure drop, while the sheet-Gyroid structure exhibitecaused the highest valuepressure loss.

DFor organifferent c PCMs (Phase Change Materials), various metallic TPMS-based struarchitectures have been used asemployed to improve thermal conductivity enhancers for organic PCMs (Phase Change Materials). It was found that th. It was found that in terms of heat transfer performance, the PCM embedded with the sheet-Primitive structure provided superiority in terms of heat transfer outperformance over ed the PCM-alone cases [36], as presented in Figure 8. Also, Quereshi et al. [37] reported that the sheet-TPMS structures showed enhanced heat transfer performance by increasing the average heat transfer coefficient and reducing theminimized melting time of the PCMPCM time. Fan et al. [38] observed that the battery temperature was sintegnificantly improved by integrating the TPMS structure into a PCM-based battery thermal management system (BTMS) achieved significant improvement in reducing th. The average battery temperature. They further combined was found to be around 40% lower with the addition of water as a working fluid for the PCM/TPMS-based BTMS, and it was found that the average battery temperature was lower than without a cooling water system by about 40%, which eliminatedeliminating the thermal saturation of the PCM.

Figure 8 Comparisons of heat flux and liquid fraction for PCM only and Primitive PCM, adapted from [36].

Recently, Qureshi et al. [39] reported for the utilization of TPMS architecturefirst time that TPMS models impregnated with PCM have been used for high heat flux cooling applications for the first time. It was observed that the under conditions of high heat flux, the TPMS-based structures mitigatedsignificantly reduced temperature under high heat flux conditions. Moreover, a change in heat sink material. Moreover, they also found that because copper has good thermal conductivity, switching from aluminum powder (AlSi10Mg) to copper showed better temperature mitigation because of the favorable thermal conductivityuse as a heat sink resulting in better temperature control.

Baobaid et al. [40] compared the solid-Diamond, solid-Gyroid and sheet-Gyroid structures for three boundary conditions. It was found that the sheet-Gyroid structure achieved superior thermal performancein the free convection. It was found that when opening the top and bottom surfaces of the enclosuree, the sheet-Gyroid structure provided better thermal performance. Still, its surface temperature was the highest when opening the sides and top surfaces. They summarized that the sheet-Gyroid structure with a larger surface area was opposed by the fflow resistance insidewithin the complex structure, causing a considerable decrease in of the sheet-Gyroid construction was very high, which significantly reduced thermal performance.

3. Effects of TPMS design variables on flow and heat transfer

3.1 Porosity

The porosity (ε) is defined as the fluid volume divided by the total volume of the cohannsidered systemel. It has been fixmostly maintained at equivalent values to compare the effects of different TPMS topologies on flow and heat transfer performance. The porosity can also values can be set to the same values forin the uniform or graded TPMS-based structures. Moreover, in many to investigationste the flow and heat transfer characteristics, the porosity of the specific TPMS topology has been varied to observe the flow and heat transfer characteristicschanged in various research.

3.1.1 Equivalent porosity

MThe majority ost research has analyzf studies have examined the flow, heat, and mass transfer under laminar flow regimes for thefor various TPMS-based structures with uniform porosity of different TPMS structurein laminar flow systems. For heat exchanger applications, Cheng et al. investigated the TPMS-based structures' morphology [41][42]. In the numerical model, the cold gas flowed in the TPMS-based structures and cooled the pore and solid matrix interface, which was heated with the constant heat flux. It was reported that thnoted that with increasing Reynolds numbers, the interstitial Nusselt number values for the sheet-Primitive structure increased slightly at higher Reynolds numbers. In contrast, tmarginally increased. The values for the sheet-Diamond, sheet-IWP, and sheet-Gyroid structures , on the other hand, increased in a quasilinear manner sincfashion because the complex curvatures broke the boundary layer.

The sheet-IWP model achieved the highest heat transfer, while the sheet-Primitive model caused the lowest values. However, it can be expected that the sheet-Diamond structures could provide the highest values when the Reynolds number is larger than 200.

Kaur and Singh [43] comparveraged hed the averaged heat transfer coefficients of the sheet-Gyroid and sheet-Primitive structures atwith an equivalent porosity for heat sink applications where the coolant flow passes the TPMS-based structure that was heated by a constant heatere compared by Kaur and Singh  flux[43]. The simulation results showed that compared to the sheet-GyroidPrimitive structure provide, the sheet-Gyroid structure had a higher heat transfer than. Even though the sheet-PrimitiveGyroid structure. Moreover, the sheet-Gyroid structure out resulted in a high-pressure loss in the channel, it performed thbetter than the sheet-Primitive structure at specific under particular pumping power conditions, even though it caused a high-pressure loss in the channel. Sreedhar et al. [33] reported that compared different solid-basedto other TPMS structures, i.e., Gyroid, Primitive, IWP, Fischer Koch S, and transverse Schwarz CLP (tCLP), at the Reynolds number of about 20–60. They reported that the soarchitectures, the solid-Gyroid structure considerably improvsignificantly increased mass transfer and reducdecreased pressure loss. Similar results were also acquired by Thomas et al. [44], which further found that although the tCLP topology exhibited a superior overall film heat transfer coefficient to thad a higher pressure loss than the other TPMS structures but caused the highest pressure loss in, it showed a better overall film heat transfer coefficient.

For thurbule nt flow system.

Ts, the flow characteristics and heat transfer caperformanceabilities of a cooling channel for heat sinks at a specific at a particular porosity have also been tested for turbulent flow regimesinvestigated. Yinzheng et al. [45] analyzshowed the heat transfer performance of the solid-Gyroid, solid-Diamond, and solid-Primitive structures. The results showed that the at due to the greater heat dissipation area in the solid-Diamond structure presente, it had the highbest heat transfer performance owing to its larger heat dissipation area. In contrast, t. The solid-Primitive structure showlattice, meanwhile, caused the lowest channel flow resistance in the channel. Al-Ketan et al. [30] compared the heat transfer performances between the solid-Gyroid, solid-Diamond, and sheet-Gyroid structures in a cooling channel heated on 4-side walls at the Reynolds number of about 4000–65,000. It was found that thound that the sheet-Gyroid structure achievedhas the highest convective heat transfer coefficient because ofdue to its complex curvatureed wall. Among these TPMS topologies, Khalil et al. [31] further observed that the sas the Reynolds number increased, the solid-Diamond structure showehad the best thermal performance as the Reynolds number increased owing to a result of reasonably increased pressure loss and significantly increasemproved heat transfer. In aAdditionally, the sheet-Gyroid structure showpresented the lowest thermal performance in the comparison since it caused the highest-pressure loss .

According the system.

o Al-Ketan et al. [30], explained that thethe variation in pressure loss variation in in the channel was due to the difference in t pore size, as demonstrateds, as seen in Figure 9,. wThere the diameter of the maximum sphere (red sphere) passing throughthat fits the smallest hole of the TPMS-based structure wais employed to describe the pore size. It can be observed that the sheet-Gyroid structure, causing the highest pressure loss, h has the smallest pore size, followed by the solid-Diamond and solid-Gyroid structures. Hence, the sheet-Gyroid structure causes the highest pressure loss.

Figure 9 The maximum sphere, passfitting through the smallest hole of different TPMS lattices: (a) Sheet-Gyroid structure; (b) Solid-Diamond structure; (c) Solid-Gyroid structure, adapted from [30].

TFor improving the effects ofcooling performance, the grading of the porosity of the TPMS-based structures have alsos been examined in several studies for enhancing the thermal performance of cooling channels. Gradedinvestigated in a number of research. The graded TPMS structure has the same overall porosity as a uniform TPMS structure is thebut gradual increase or decrease of ly changes the TPMS porosity along the channel’s llength, width, or height, which remains the same overall porosity as the uniform TPMS ones of the channel.

Qureshi et al. [46] showed that in terms ofor the sheet-Primitive, sheet-Gyroid, and sheet-IWP structur conductive and convective heat transfer capabilities, the gradually increased porosity along the flow direction outperformed the equivalent ununiform and gradually decreased porosity models in terms of conductive and convective heat transfer performancefor different sheet-TPMS structures. Moreover, Al-Ketan et al.  [30] reported that under the graded-urbulent flow regimes, the solid Diamond structure with porosity varyingied from 80.0–-82.5% along the flow direction under turbulent flow regimes rereduced the pressure loss by aboutroughly 27.6%, while only reducing the overall heat transfer coefficient decreased by only by 15.7%.

Figure 10 shows the velocity vector for uniform and graded diamond-solid structures, investigated by Al-Ketan et al.  [30]. As seen the Figure 10a, for the uniform structure, the velocity increases gradually due to the fluid expansion. In the case with negative grading porosity in Figure 10b, the velocity entering the high porosity structure is lower than the corresponding uniform one. This reduction is attributed to the small structure that lesser disturbs the incoming fluid. However, a higher velocity can be observed as the structure is larger downstream. The velocity distribution in this channel is non-uniform as compared to the others. For the case with a positive grading structure in Figure 10c, the velocity increases significantly when the fluid enters the low porosity structure. The velocity magnitude remains similar throughout the channel, indicating better uniformity distribution of the flow.

Figure 10 Velocity vectors of the uniform and graded diamond-solid structures at Re = 65,326, studied by Al-Ketan et al. [30].

TAlthough the graded TPMS structures were conceived with showed reasonable heat transfer reductions but provide a better, they offer higher cooling channel thermal performance of cooling channels. T. Also, the graded TPMS-based structures improve thermal performance and showresulted in lighter cooling channels by using less material consumption in during additive manufacturing, rendering lightweight cooling channels. Howevere. However, due to other crucial factors like mechanical strength, hydraulic performance, etc., the graded TPMS-based structures might not be better than the corresponding superior to the uniform ones for particular functions due to other important considerations,some functions e.g., mechanical strength, hydraulic performance, etc. [47].

3.1.2 Varying the porosity

The overall contact area is significantly impacted by the porosity variation for a specific TPMSTPMS-based structure considerably affects the overall contact area, changing , which influences the flow, heat, and mass transfer. Sreedhar et al.The solid-Gyroid model [33]with vagried theeater porosity of the solid-Gyroid structure in the range of 72–90%. It was reported that the solid-Gyroid, according to Sreedhar et al. model[33], withas larger porosityobserved to significantly improvedenhance mass transfer and loweredreduce pressure loss. However, several studies observed thatdifferent investigations found that the porosity of the sheet-TPMS structures had an inverse relationship with the convective heat transfer coefficient and friction factor inversely varies with the porosity of the sheet-TPMS structures [48][49].

Qureshi et al. [46] found that the rconvectiveduction in and conductive heat transfer were significantly improved in a lower porosity for the sheet-Primitive, sheet-Gyroid, and sheet-IWP structures considerably en. Similarly, Cheng et al. [41] reported thanct thed conductive and interstitial convective heat transfer. Similarly, Cheng et al. [41] coefficient reportduced that as the porosity increased for the sheet-IWP, sheet-Diamond, and sheet-Gyroid structures, the interstitial convective heat transfer coefficient decreased since t because the velocity dropped in the channel aeclined at the larghigher porosity. However, the convectivedue to the larger heat transfer coefficient for area at the higher porosity values in the sheet-Primitive structure increased at the higher porosity values due to the larger , the convective heat transfer area, as showncoefficient increased, as illustrated in Figure 11.

Figure 11 Effect of porosity on convective heat transfer coefficient for different TPMS structures at Re = 40, adapted from [41].

3.2 Wall thickness

Concerning additive manufacturing for cooling cThannels, the e relative wall thickness (t) of dvarifferentous TPMS topologies has been set to investigatdefined in order to explore the effects on the flow and heat transfer performance. It should be noted that due to topology differences, the values of porosity (ε), pore size (d_pore), and surface area at c = 0 (A_TPMS) are vcharinged for each TPMS surfacetopology at a homogenous wall thickness and unit cell size [50], as shown in Figure 12. AIt the same wall thickness of t = 0.1 mm cand unit cell size of L = 2.0 mm, the porobe obsity, pore size, and surface area of TPMS varied significantly in different TPMS topologies. Trved that the sheet-Diamond structure has the largest surface area withand the same pore size as the sheet-Gyroid structure, whileereas the sheet-Primitive structure has the least area withowest surface area and the largest pore size.

Figure 12 Variations in porosity, pore size, and the surface of TPMS at c = 0 at the wall thickness of t = 0.1 mm and unit cell size of L = 2.0 mm for a unit cell of sheet-based TPMS structures (The correlations for the porosity, pore size and surface area are provided by Poltue et al. [50]): (a) Sheet-Gyroid; (b) Sheet-Primitive; (c) Sheet-Diamond; (d) Sheet-IWP structures.

In the laminar flow system, accoregime 15,ding to Femmer et al. [51] reported that at the same thickness of 0.4 mm, the heat exchanger with the sheet-Diamond structure achieved a higher heat transfer outperformance for inherent pressure loss compared to ted the sheet-Gyroid, sheet-IWP, and sheet-Primitive structures. Similar result in terms of heat transfer performance for inherent pressure loss. Similar findings were reported by Passos [48], in which the best thermal performance was ho found inthat the sheet-Diamond structure. Genç et al. [49] observe had thate at the lowest thickness of 0.16best thermal performance. Genç et al. mm,[49] nothe friction factors of ed that the sheet-Diamond structure generatproduced the highest pressure loss compared to the sheet-Gyroid and sheet-Primitive structures. Moreover Additionally, for all TPMS designs, the friction factor decreased with increasingreduced as the Reynolds number for all TPMS geometriesincreased.

Iyer et al. [52] reported that the lowesheett values of the Nusselt numbers were found in the sheet-Primitive structure caused the lowest Nusselt number, as shown in vFigure 13alues. In contrastMeanwhile, the sheet-Diamond structure haexhibited the best heat transfer performance, followed by the C(I₂-Y**),. as plottedAs shown in Figure 13a. For the friction factor, the sheet-Neovius structure caused the highest values, followed by the sheet-FRD structure, while, the other TPMS structures provided a comparable pressure loss within the Reynolds numbers varyingrange between 0–300, as illustrated in-300, whereas the sheet-Neovius structure caused the highest values, followed Figure 13b.y the Theysheet-FRD structure. It was also reported that the predictions of the pressure losses are lower than Femmer et al.  [51] and Kaur and Singh [43] because of smaller frictional pressure loss from the semi-infinite curvatures in their simulationsed wall of the TPMS structures has been set.

Figure 13 Comparisons of the Nusselt number and friction factor of different TPMS topologies for the same infinitesimally thin walls (The correlations are provided by Iyer et al. [52]): (a) Averaged Nusselt numbers; (b) Friction factors.

FAccor higher Reynolds numbers, ding to Li et al. [53], compared the flow and heat transfer characteristics of the sheet-Gyroid and sheet-Diamond structures for a homogenous wall thickness of 0.7 mm. It was reported that the thermal perthe thermal performance of the sheet-Gyroid structure was higher thansuperior to the sheet-Diamond model. The different results from the previous investigations [48][51] at high Reynolds numbers. The substantial increan be attributed to the large tse in turbulent kinetic energy (TKE) generation due to the fluid mixing at high Reynolds numbers in the sheet-Gyroid structure. This intensive fluid mixing was preferable for heat is the reason that makes high heat transfer, which shows the different results from the earlier investigations [48][51].

Attaransfer enhazadeh et al. [54] incvement.

Tstigated the diefferentcts of varying thicknesses of the sheet-Diamond structure on the flow and heat transfer performance for a heat sink cooling channel under laminar flow were studied by Attarzadeh et al. [54]. They rclaimeported that while the larger wall thickness provided a higherincreased the convective heat transfer coefficient; however, a considerably large wall thickness block, it impeded the flow field, decreaslowering the thermal performance of the cooling channels. As shown in Figure 14, a illustrates the continuous decayal decline of reverse flow in the channel was observed, which reduced the lowers pressure loss when decreasing as the wall thickness. The lowest thickness showed the best thermal performance d is decreased. Due to low-pressure loss and a moderate increase in heat transfer in the channel, the lowest thickness demonstrates the best thermal performance in their simulations.

Figure 14 Demonstrations of reverse flow regions for small thickness (left) and large thickness (right) of the sheet-Diamond structure at a specific Reynolds number [54].

Later, to find the optimal configurations, Attarzadeh et al. [55] investudiigated a multi-objective optimization workflowapproach based on a Genetic Algorithm for laminar flow to reveal the optimal configurations. The sheet-Gyroid structure was selected to studychosen to investigate the TPMS design variables. It was observedshown that increasing wall thickness improvedbetter thermal performance. They also suggeste resulted from thicker walls. Additionally, they claimed that the pore size and the wall thickness of the TPMS structure were the moexhibited the greatest Pareto- sensitive inity during the optimization. It should be marked that the results did not conflict with the previous findings by Attarzadeh et al. [54] noted that since the TPMS topologies and unit cell sizes usemployed in the study are different, presenting different results betweenthe results did not disagree with the earlier findings by Attarzadeh et al. them[54].

3.3 Unit cell size

The effects of unit cell size for the TPMS topologies onaffecting the flow and heat transfer performances are rarely foundiscussed in the literature. According to Zimmer et al. [56] investigated the pressure loss in three different unit cell sizes of the sheet-Diamond structure at 8 mm, 4 mm, and 2 mm They reported that th the largest unit cell sizes generatcaused the low-pressure loss in the system, whileereas the smallest one considerabsignificantly increased pressure loss, particularespecially at higher velocities. Similarly to this, Al-Ketan et al. [35] fdiscounvered that at the same wall thickness of 0.6 mm, the sheethe sheet-Gyroid and sheet-Primitive structures with the smaller unit cell size caused higher pressure loss because of more complexicated geometries and lower porosities. Attarzadeh et al. [55] investigated three different cell sizes of the sheet-Gyroid structure shown in aFigure 15, cooling channel. They reported that decreasing the unit cell size improved the thermal performance of the heat exchanger. It can be deducedt can be inferred that a smaller unit cell size caused resulted in higher pressure loss due tobecause of the lower porosity but achieved higherincreased heat transfer due to the larger specific surface areas (Sv). Later, according to Attarzadeh et al. [55], reducing the unit cell size shown in Figure 15enhanced the thermal performance of the heat exchanger. 

Figure 15 The sheet-Gyroid structures with different unit cell sizes at the same thickness of 0.6 mm, adapted from [35].

4. Conclusion

ERecent extensive studieperimental and numerical investigations have been reviewextensively analyzed to showhighlight the effects on flow and heat transfer enhancement in cooling channels with tTriply pPeriodic mMinimal sSurfaces (TPMS) from recent experimental and numerical studies. The extensive results include the effects of porosity. The effects of wall thickness, porosity and unit cell size on the flow field and heat transfer, followed by the effects of wall thickness and unit cell size. T from the extensive results. are demonstrated and discussed. The following are the main conclusions are drawn as follows:

1. With the same porosity, as the Reynolds numbers increase, more complicated TPMS topologies, such as the Diamond and Gyroid models, achieve high heat transfer but result in substantial pressure loss. Their tortuous topologies and greater surface areas, which significantly alter the flow characteristics, are the main reason for this increase. The graded TPMS-based structure that increases the porosity along the flow direction presents higher thermal performance than the uniform one due to lower pressure loss while maintaining high heat transfer in the channel.
2. The porosity in the majority of the sheet-TPMS structures has an inverse relationship to the convective heat transfer coefficient and the friction factor. Except for the sheet-Primitive structure, a high-speed velocity area along the flow direction interacts with the heating walls in the lower porosity model.
3. With the same wall thickness, different TPMS structures show a difference in the porosity and surface area, which changes flow and heat transfer characteristics in the channel. Under laminar flow, the Diamond structure provides the best thermal performance. In contrast, for turbulent flow systems, the Gyroid obtains better heat transfer because of increased turbulent kinetic energy. However, due to the TPMS topologies and unit cell sizes, the wall thickness variation affects the flow field and heat transfer enhancement differently. However, most of the research found that the larger wall thickness exhibits larger convective heat transfer and pressure loss.
4. With the same porosity, more complex TPMS topologies, e.g., Diamond and Gyroid models, achieve high heat transfer as the Reynolds numbers increase but cause high-pressure loss. This increase is due to their tortuosity topologies and larger surface areas, considerably changing the flow characteristics. For heat sink applications, the graded TPMS-based structure along the flow direction provides better thermal performance than the uniform one due to decreased pressure loss with maintaining high heat transfer in the channel.
5. The convective heat transfer coefficient and friction factor inversely change with the porosity for most of the sheet-TPMS structures, except for the Primitive model, because a large high-speed velocity area occurs in the lower porosity model along the flow direction, significantly interacting with the heating walls.
6. Different TPMS topologies with the same wall thickness have different porosities and surface areas, leading to flow and heat transfer variation. Under laminar flow, the Diamond heat exchanger shows the best thermal performance, while for turbulent flow regimes, the Gyroid heat transfer obtains better because of increased turbulent kinetic energy. The larger wall thickness shows higher convective heat transfer and pressure loss; however, owing to the TPMS topologies and unit cell sizes, the wall thickness variation affect the flow field and heat transfer enhancement differently.

References

[1] C. Pan, Y. Han, J. Lu, Design and optimization of lattice structures: A review, Appl. Sci. 10 (2020) 1–36. https://doi.org/10.3390/APP10186374.

[2] I. Kaur, P. Singh, State-of-the-art in heat exchanger additive manufacturing, Int. J. Heat Mass Transf. 178 (2021) 121600. https://doi.org/10.1016/j.ijheatmasstransfer.2021.121600.

[3] I. Kaur, P. Singh, Critical evaluation of additively manufactured metal lattices for viability in advanced heat exchangers, Int. J. Heat Mass Transf. 168 (2021). https://doi.org/10.1016/j.ijheatmasstransfer.2020.120858.

[4] O. Al-Ketan, R.K. Abu Al-Rub, Multifunctional Mechanical Metamaterials Based on Triply Periodic Minimal Surface Lattices, Adv. Eng. Mater. 21 (2019) 1–39. https://doi.org/10.1002/adem.201900524.

[5] H.A. Schwarz, Gesammelte Mathematische Abhandlungen, Springer, Berlin, Germany, 1890.

[6] E.R. Neovius, Bestimmung Zweier Spezieller Periodischer Minimalflächen, Akad. Abhandlungen, Helsinki, Finland, 1883.

[7] A.H. Schoen, Infinite Periodic Minimal Surfaces Without Self-Intersections, United States, 1970. https://doi.org/10.1057/9781137465160.0020.

[8] M. Speirs, B. Van Hooreweder, J. Van Humbeeck, J.P. Kruth, Fatigue behaviour of NiTi shape memory alloy scaffolds produced by SLM, a unit cell design comparison, J. Mech. Behav. Biomed. Mater. 70 (2017) 53–59. https://doi.org/10.1016/j.jmbbm.2017.01.016.

[9] K.A. Khan, R.K. Abu Al-Rub, Time dependent response of architectured Neovius foams, Int. J. Mech. Sci. 126 (2017) 106–119. https://doi.org/10.1016/j.ijmecsci.2017.03.017.

[10] N. Wang, G.K. Meenashisundaram, S. Chang, J.Y.H. Fuh, S.T. Dheen, A. Senthil Kumar, A comparative investigation on the mechanical properties and cytotoxicity of Cubic, Octet, and TPMS gyroid structures fabricated by selective laser melting of stainless steel 316L, J. Mech. Behav. Biomed. Mater. 129 (2022) 105151. https://doi.org/10.1016/j.jmbbm.2022.105151.

[11] F. Teng, Y. Sun, S. Guo, B. Gao, G. Yu, Topological and Mechanical Properties of Different Lattice Structures Based on Additive Manufacturing, Micromachines. 13 (2022) 1017. https://doi.org/10.3390/mi13071017.

[12] D. Ali, M. Ozalp, S.B.G. Blanquer, S. Onel, Permeability and fluid flow-induced wall shear stress in bone scaffolds with TPMS and lattice architectures: A CFD analysis, Eur. J. Mech. - B/Fluids. 79 (2020) 376–385. https://doi.org/10.1016/j.euromechflu.2019.09.015.

[13] H. Montazerian, M. Zhianmanesh, E. Davoodi, A.S. Milani, M. Hoorfar, Longitudinal and radial permeability analysis of additively manufactured porous scaffolds: Effect of pore shape and porosity, Mater. Des. 122 (2017) 146–156. https://doi.org/10.1016/j.matdes.2017.03.006.

[14] H.L. Liu, W.R. Hwang, Permeability prediction of fibrous porous media with complex 3D architectures, Compos. Part A Appl. Sci. Manuf. 43 (2012) 2030–2038. https://doi.org/10.1016/j.compositesa.2012.07.024.

[15] X. Huang, W. Zhou, D. Deng, Effective diffusion in fibrous porous media: A comparison study between lattice boltzmann and pore network modeling methods, Materials (Basel). 14 (2021) 1–14. https://doi.org/10.3390/ma14040756.

[16] F. Wang, H. Jiang, Y. Chen, X. Li, Predicting thermal and mechanical performance of stochastic and architected foams, Int. J. Heat Mass Transf. 171 (2021) 121139. https://doi.org/10.1016/j.ijheatmasstransfer.2021.121139.

[17] L. Ni, Z. Chen, P. Mukhopadhyaya, X. Zhang, Q. Wu, Q. Yu, G. Miu, Numerical simulation on thermal performance of vacuum insulation panels with fiber /powder porous media based on CFD method, Int. J. Therm. Sci. 172 (2022) 107320. https://doi.org/10.1016/j.ijthermalsci.2021.107320.

[18] Z.A. Qureshi, S.A.B. Al-Omari, E. Elnajjar, O. Al-Ketan, R.A. Al-Rub, Using triply periodic minimal surfaces (TPMS)-based metal foams structures as skeleton for metal-foam-PCM composites for thermal energy storage and energy management applications, Int. Commun. Heat Mass Transf. 124 (2021) 105265. https://doi.org/10.1016/j.icheatmasstransfer.2021.105265.

[19] S. Catchpole-Smith, R.R.J. Sélo, A.W. Davis, I.A. Ashcroft, C.J. Tuck, A. Clare, Thermal conductivity of TPMS lattice structures manufactured via laser powder bed fusion, Addit. Manuf. 30 (2019) 100846. https://doi.org/10.1016/j.addma.2019.100846.

[20] C. Beyer, D. Figueroa, Design and Analysis of Lattice Structures for Additive Manufacturing, J. Manuf. Sci. Eng. Trans. ASME. 138 (2016) 1–15. https://doi.org/10.1115/1.4033957.

[21] D. Liang, G. He, W. Chen, Y. Chen, M.K. Chyu, Fluid flow and heat transfer performance for micro-lattice structures fabricated by Selective Laser Melting, Int. J. Therm. Sci. 172 (2022) 107312. https://doi.org/10.1016/j.ijthermalsci.2021.107312.

[22] D.W. Abueidda, R.K. Abu Al-Rub, A.S. Dalaq, D.W. Lee, K.A. Khan, I. Jasiuk, Effective conductivities and elastic moduli of novel foams with triply periodic minimal surfaces, Mech. Mater. 95 (2016) 102–115. https://doi.org/10.1016/j.mechmat.2016.01.004.

[23] V. V. Calmidi, R.L. Mahajan, The effective thermal conductivity of high porosity fibrous metal foams, J. Heat Transfer. 121 (1999) 466–471. https://doi.org/10.1115/1.2826001.

[24] R. Wulf, M.A.A. Mendes, V. Skibina, A. Al-Zoubi, D. Trimis, S. Ray, U. Gross, Experimental and numerical determination of effective thermal conductivity of open cell FeCrAl-alloy metal foams, Int. J. Therm. Sci. 86 (2014) 95–103. https://doi.org/10.1016/j.ijthermalsci.2014.06.030.

[25] M.I. Hassan Ali, O. Al-Ketan, N. Baobaid, K. Khan, R.K. Abu Al-Rub, A study on the fluid flow and heat transfer for a porous architected heat sink using the idea of CFD modelling, ASME Int. Mech. Eng. Congr. Expo. Proc. 8 (2019) 1–6. https://doi.org/10.1115/IMECE2019-11498.

[26] M.I. Hassan Ali, O. Al-Ketan, A. Alhammadi, M. Khalil, K. Khan, R.K. Abu Al-Rub, Heat transfer characterization of 3D printable architected heat sinks, in: ASME Int. Mech. Eng. Congr. Expo. Proc., 2019: pp. 1–6. https://doi.org/10.1115/IMECE2019-11523.

[27] Y. Rao, Y. Feng, B. Li, B. Weigand, Experimental and numerical study of heat transfer and flow friction in channels with dimples of different shapes, J. Heat Transfer. 137 (2015) 1–10. https://doi.org/10.1115/1.4029036.

[28] Y. Li, Y. Rao, D. Wang, P. Zhang, X. Wu, Heat transfer and pressure loss of turbulent flow in channels with miniature structured ribs on one wall, Int. J. Heat Mass Transf. 131 (2019) 584–593. https://doi.org/10.1016/j.ijheatmasstransfer.2018.11.067.

[29] Y. Rao, S. Zang, Flow and Heat Transfer Characteristics in Latticework Cooling Channels With Dimple Vortex Generators, J. Turbomach. 136 (2014) 1–10. https://doi.org/10.1115/1.4025197.

[30] O. Al-Ketan, M. Ali, M. Khalil, R. Rowshan, K.A. Khan, R.K. Abu Al-Rub, Forced Convection Computational Fluid Dynamics Analysis of Architected and Three-Dimensional Printable Heat Sinks Based on Triply Periodic Minimal Surfaces, J. Therm. Sci. Eng. Appl. 13 (2021) 1–14. https://doi.org/10.1115/1.4047385.

[31] M. Khalil, M.I. Hassan Ali, K.A. Khan, R. Abu Al-Rub, Forced convection heat transfer in heat sinks with topologies based on triply periodic minimal surfaces, Case Stud. Therm. Eng. 38 (2022) 102313. https://doi.org/10.1016/j.csite.2022.102313.

[32] N. Thomas, N. Sreedhar, O. Al-Ketan, R. Rowshan, R.K. Abu Al-Rub, H. Arafat, 3D printed spacers based on TPMS architectures for scaling control in membrane distillation, J. Memb. Sci. 581 (2019) 38–49. https://doi.org/10.1016/j.memsci.2019.03.039.

[33] N. Sreedhar, N. Thomas, O. Al-Ketan, R. Rowshan, H.H. Hernandez, R.K. Abu Al-Rub, H.A. Arafat, Mass transfer analysis of ultrafiltration using spacers based on triply periodic minimal surfaces: Effects of spacer design, directionality and voidage, J. Memb. Sci. 561 (2018) 89–98. https://doi.org/10.1016/j.memsci.2018.05.028.

[34] R.K. Abu Al-Rub, O. Al-Ketan, Catalytic converter substrates comprising triply periodic minimal surfaces, US2019/0145298A1, 2019. https://patentimages.storage.googleapis.com/b6/eb/3b/4e24fd37612678/US20190145298A1.pdf.

[35] O. Al-Ketan, M. Pelanconi, A. Ortona, R.K. Abu Al-Rub, Additive manufacturing of architected catalytic ceramic substrates based on triply periodic minimal surfaces, J. Am. Ceram. Soc. 102 (2019) 6176–6193. https://doi.org/10.1111/jace.16474.

[36] Z.A. Qureshi, S.A.B. Al Omari, E. Elnajjar, F. Mahmoud, O. Al-Ketan, R.A. Al-Rub, Thermal characterization of 3D-Printed lattices based on triply periodic minimal surfaces embedded with organic phase change material, Case Stud. Therm. Eng. 27 (2021) 101315. https://doi.org/10.1016/j.csite.2021.101315.

[37] Z.A. Qureshi, E. Elnajjar, O. Al-Ketan, R.A. Al-Rub, S.B. Al-Omari, Heat transfer performance of a finned metal foam-phase change material (FMF-PCM) system incorporating triply periodic minimal surfaces (TPMS), Int. J. Heat Mass Transf. 170 (2021). https://doi.org/10.1016/j.ijheatmasstransfer.2021.121001.

[38] Z. Fan, R. Gao, S. Liu, Thermal conductivity enhancement and thermal saturation elimination designs of battery thermal management system for phase change materials based on triply periodic minimal surface, Energy. 259 (2022) 125091. https://doi.org/10.1016/j.energy.2022.125091.

[39] Z. Ahmed Qureshi, S. Addin Burhan Al-Omari, E. Elnajjar, O. Al-Ketan, R. Abu Al-Rub, Architected Lattices Embedded with Phase Change Materials for Thermal Management of High-Power Electronics: A Numerical Study, Appl. Therm. Eng. 219 (2022) 119420. https://doi.org/10.1016/j.applthermaleng.2022.119420.

[40] N. Baobaid, M.I. Ali, K.A. Khan, R.K. Abu Al-Rub, Fluid flow and heat transfer of porous TPMS architected heat sinks in free convection environment, Case Stud. Therm. Eng. 33 (2022) 101944. https://doi.org/10.1016/j.csite.2022.101944.

[41] Z. Cheng, X. Li, R. Xu, P. Jiang, Investigations on porous media customized by triply periodic minimal surface: Heat transfer correlations and strength performance, Int. Commun. Heat Mass Transf. 129 (2021) 105713. https://doi.org/10.1016/j.icheatmasstransfer.2021.105713.

[42] Z. Cheng, R. Xu, P.X. Jiang, Morphology, flow and heat transfer in triply periodic minimal surface based porous structures, Int. J. Heat Mass Transf. 170 (2021) 120902. https://doi.org/10.1016/j.ijheatmasstransfer.2021.120902.

[43] I. Kaur, P. Singh, Flow and thermal transport characteristics of Triply-Periodic Minimal Surface (TPMS)-based gyroid and Schwarz-P cellular materials, Numer. Heat Transf. Part A Appl. 79 (2021) 553–569. https://doi.org/10.1080/10407782.2021.1872260.

[44] N. Thomas, N. Sreedhar, O. Al-Ketan, R. Rowshan, R.K. Abu Al-Rub, H. Arafat, 3D printed triply periodic minimal surfaces as spacers for enhanced heat and mass transfer in membrane distillation, Desalination. 443 (2018) 256–271. https://doi.org/10.1016/j.desal.2018.06.009.

[45] Z. Yinzheng, Numerical Analysis On Fluid-solid Coupling Cooling Of Minimal Surface Lattice Structure, J. Phys. Conf. Ser. 1187 (2019) 032070. https://doi.org/10.1088/1742-6596/1187/3/032070.

[46] Z.A. Qureshi, S. Addin Burhan Al-Omari, E. Elnajjar, O. Al-Ketan, R.A. Al-Rub, On the effect of porosity and functional grading of 3D printable triply periodic minimal surface (TPMS) based architected lattices embedded with a phase change material, Int. J. Heat Mass Transf. 183 (2022) 122111. https://doi.org/10.1016/j.ijheatmasstransfer.2021.122111.

[47] C. Karuna, T. Poltue, S. Khrueaduangkham, P. Promoppatum, Mechanical and fluid characteristics of triply periodic minimal surface bone scaffolds under various functionally graded strategies, J. Comput. Des. Eng. 9 (2022) 1258–1278. https://doi.org/10.1093/jcde/qwac052.

[48] A.G.P. Passos, Laminar flow and heat transfer in triply periodic minimal surfaces, Lund University, Lund, Sweden, 2020. https://fenix.tecnico.ulisboa.pt/downloadFile/1126295043836646/ThesisAndrePass%0Aos.pdf.

[49] A. Mete Genç, C. Vatansever, M. Koçak, Z. Haktan Karadeniz, Investigation of additively manufactured triply periodic minimal surfaces as an air-to-air heat exchanger, in: REHVA 14th HVAC World Congr., Rotterdam, Natherlands, 2022. https://doi.org/https://doi.org/10.34641/clima.2022.172

[50] T. Poltue, C. Karuna, S. Khrueaduangkham, S. Seehanam, P. Promoppatum, Design exploration of 3D-printed triply periodic minimal surface scaffolds for bone implants, Int. J. Mech. Sci. 211 (2021) 106762. https://doi.org/10.1016/j.ijmecsci.2021.106762.

[51] T. Femmer, A.J.C. Kuehne, M. Wessling, Estimation of the structure dependent performance of 3-D rapid prototyped membranes, Chem. Eng. J. 273 (2015) 438–445. https://doi.org/10.1016/j.cej.2015.03.029.

[52] J. Iyer, T. Moore, D. Nguyen, P. Roy, J. Stolaroff, Heat transfer and pressure drop characteristics of heat exchangers based on triply periodic minimal and periodic nodal surfaces, Appl. Therm. Eng. 209 (2022) 118192. https://doi.org/10.1016/j.applthermaleng.2022.118192.

[53] W. Li, G. Yu, Z. Yu, Bioinspired heat exchangers based on triply periodic minimal surfaces for supercritical CO2 cycles, Appl. Therm. Eng. 179 (2020) 115686. https://doi.org/10.1016/j.applthermaleng.2020.115686.

[54] R. Attarzadeh, M. Rovira, C. Duwig, Design analysis of the ”Schwartz D” based heat exchanger: A numerical study, Int. J. Heat Mass Transf. 177 (2021) 121415. https://doi.org/10.1016/j.ijheatmasstransfer.2021.121415.

[55] R. Attarzadeh, S.H. Attarzadeh-Niaki,C. Duwig, Multi-objective optimization of TPMS-based heat exchangers for low-temperature waste heat recovery, Appl. Therm. Eng. 212 (2022) 118448. https://doi.org/10.1016/j.applthermaleng.2022.118448.

[56] A. Zimmer, J.D. PachecoAraújo, K.A. Andreassen, C.A. Grande, Effect of Manufacturing Techniques in Pressure Drop on Triple Periodical Minimal Surface Packings, Chemie-Ingenieur-Technik. 93 (2021) 967–973. https://doi.org/10.1002/cite.202000237