PUFs and Their Operational Mechanism

1. PUFs and Their Operational Mechanism

Physical(ly) Unclon(e)able Functions (PUFs) are instances of hardware modules that ideally act as one-way functions, each of which provides a different output for the same input. Therefore, each PUF instance ideally implements a unique function, making its reproduction hard to achieve and, in this way, leading to a notion of unclon(e)ability.

The implementation of PUFs is usually based on the existence of minor imperfections in hardware modules produced using the exact same manufacturing process. Such imperfections do not affect the normal operation of the hardware module in a notic(e)able way, but introduce unique (secondary) characteristics. These characteristics are then exploited under specific conditions, being referred to as the

challenge

 that is fed into the PUF, in order to extract a unique (binary)

response from the hardware module, based on its unique imperfections and characteristics.

from the hardware module, based on its unique imperfections and characteristics (Figure 1).

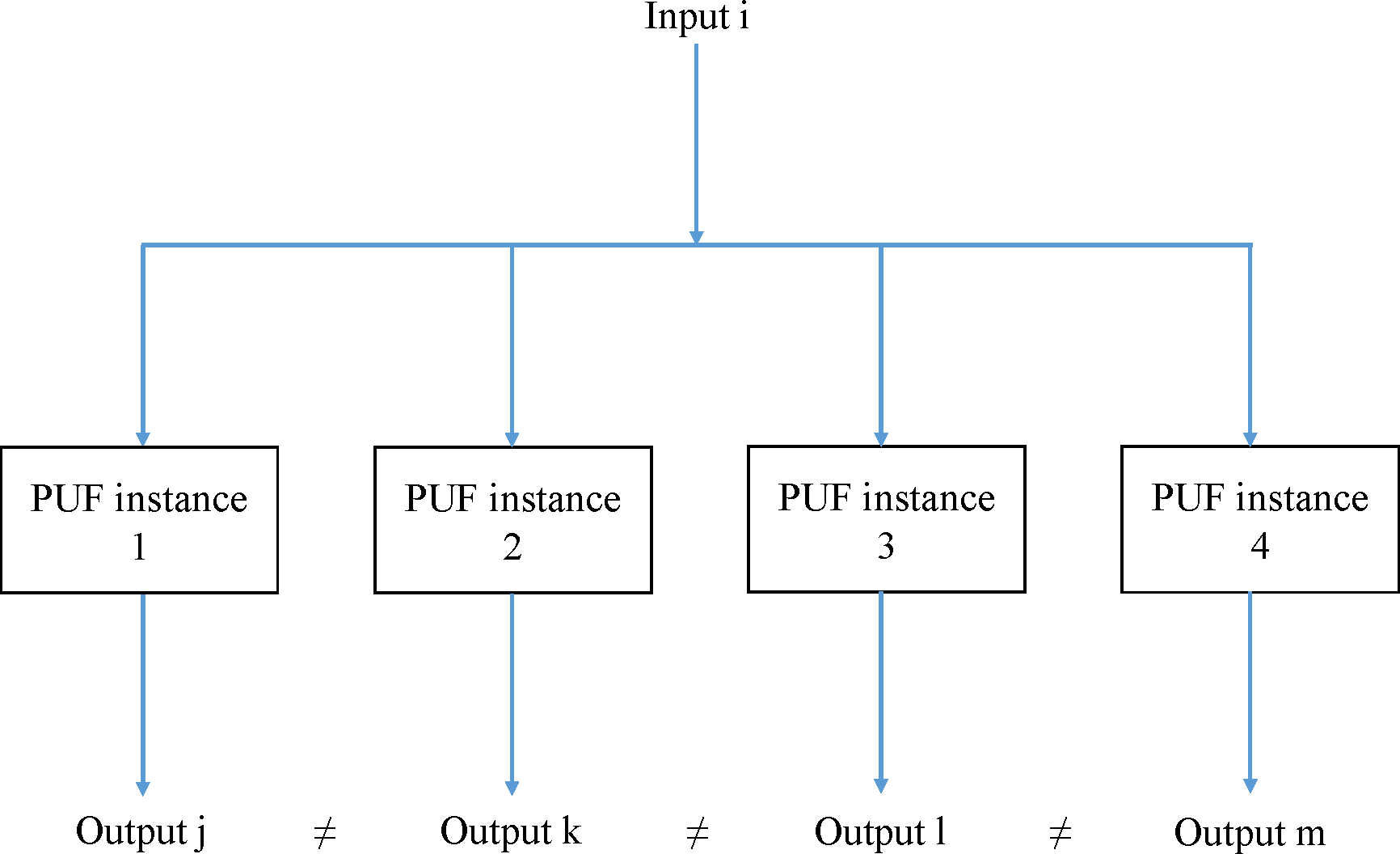
Operational mechanism of PUFs.

Figure 1. Operational mechanism of PUFs.

 PUF Implementations and Metrics

2. PUF Implementations and Metrics

A number of hardware modules and characteristics have been utilised for the implementation of PUFs, such as the unique reflection of optical materials

^[1]

, the delay characteristics of arbiters

^[2][3]

and ring oscillators

^[4]

, the capacitance of coating materials 

^[5]

, the start-up values of SRAMs 

^[6][7]

and DRAMs 

^[8]

and the decay characteristics of DRAM cells 

^[9][10][11]

. The concept of a physical one-way function can also be traced in literature dating from many decades ago

^[1]

.

PUFs are usually classified into

weak

ones, which provide a single or very few Challenge-Response Pairs (CRPs), and

strong

ones, which provide such a large number of CRPs that their complete characterisation within a limited time frame is not possible

^[12]

. Although this classification is important regarding the level of security a PUF can provide, it is also not always completely clear whether a PUF implementation can be considered as weak or strong, as well-known "strong" PUFs have proven vulnerable to modelling or machine learning attacks performed within limited time and, the number of CRPs that can be considered large enough to prevent the complete characterisation of a PUF, obviously, differs for each implementation.

PUFs have proven to be an important security primitive that can be used for cryptographic applications, especially in devices that are resource-constrained and cannot support other security mechanisms.  However, a number of attacks against them have brought their role as an adequate security mechanism into question. Therefore, current research is focused on the examination of novel PUF implementations with potentially better quality characteristics and/or the improvement of currently available ones. In general, since PUFs have been proven not to be unclon(e)able, the acronym "PUF" should rather stand for Physical

Unique

Functions, as uniqueness is a rather intrinsic property of any PUF, much like to its physical nature.

Well-known metrics used to assess the quality of the PUF responses include their Hamming weight, intra-device Hamming distance, inter-device Hamming distance, Shannon (binary) entropy and min-entropy. In practice, the values of the Hamming weight, intra-device Hamming distance and inter-device Hamming distance metrics are divided by the total number of elements (bits) contained in the PUF responses being examined, and their 

fractional

 equivalents are considered. Ideally, PUF responses would have a fractional Hamming weight of 0.5, a fractional intra-device Hamming distance of 0 (or ~0.1, considering error correction methods), a fractional inter-device Hamming distance of 0.5, a Shannon (binary) entropy of 1 and a min-entropy of 1. In practice, only certain instances of the PUFs that are based on the start-up values of SRAMs have been able to approach these ideal values. Since the responses of the PUFs that are based on the decay characteristics of DRAM cells are most often extremely biased, exhibiting a low entropy, the intra-device Jaccard index and the inter-device Jaccard index metrics have been proposed to replace the intra-device Hamming distance and inter-device Hamming distance metrics, as quality assessment metrics for these PUFs. Again, in practice, the

fractional

 intra-device Jaccard index and the

fractional

inter-device Jaccard index metrics are utilised for this purpose.

Moreover, it should also be mentioned that the responses of a particular PUF for a specific challenge at different times typically incorporate a certain degree of noise. Therefore, quite often, fuzzy schemes, such as fuzzy extractors

^[13][14]

, are employed in order to stabilise the PUF responses and usually, at the same time, convert them to bit strings of full binary entropy, which can then be used in cryptography, as keys, identifiers, etc.

 PUF Applications

3. PUF Applications

Common applications of PUFs proposed in the relevant literature include  identification, authentication, attestation, secure boot, anti-counterfeiting and secure key agreement protocols. Additionally, PUFs can also serve as the basis for the implementation of true random number generators. PUFs can also be combined with other security primitives and entropy sources, so that the overall construction will produce a different unique response for the same challenge, when queried at different times. In this case, the overall construction is referred to, in the relevant literature, as a

reconfigurable

PUF.

 Finally, in order to use PUFs in security protocols, most often an

enrollment

phase is required, during which one or some of the protocol's parties (most often the server) gains access to the PUF's CRPs and then one of the other parties (most often the client) acquires exclusive access to the PUF module. Nevertheless, it has been proven that it is impossible to achieve secure cryptographic protocols without any setup assumptions

^[15]

and, therefore, it is not possible to establish a security protocol without somehow exchanging some information first. Hence, in the case of PUFs, it is required that all parties have acquired knowledge on the PUF's CRPs or can directly access the PUF, in order for PUF-based protocols to work correctly. This setup phase, the enrollment phase, is most often followed by a

reconstruction

phase, during which the party that now has exclusive access to the PUF (re)constructs the PUF-based secret, which may be either a raw PUF response or a PUF-based token, identifier, key, etc. Then, the value of the secret (re)constructed by the party that now has exclusive access to the PUF (EA party) is directly or indirectly compared to the value of the secret acquired or constructed by the party or parties that have accessed to the PUF's CRPs during the enrollment phase (ENR party/parties). For example, if the secret is a raw PUF response and the PUF considered is a strong PUF, then the response acquired by the EA party can be directly transmitted to the ENR party/parties and compared to the response they had acquired during the enrollment phase. However, if the secret is a PUF-based key, the EA party can encrypt a nonce with the key based on its PUF response and transmit it to the ENR party/parties, which will then decrypt it with the key based on the response they had acquired during the enrollment phase. Of course, all the CRPs required in order for these protocols to function correctly need to have been acquired by all ENR parties during the enrollment phase.