Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Camila Xu and Version 1 by Rafia Nishat Toma.
A knowledge-based feature extraction technique has been developed by Bruna and Malat named wavelet scattering transform (WST), which utilizes complex wavelets to balance the discrimination ability and stability of the time-frequency domain signal.
- artificial neural network
- bearing fault diagnosis
- condition monitoring
1. Introduction
Induction motors (IMs) are widely used rotating machinery in the manufacturing and power industries, due to their certain advantages such as low cost, easy controlling mechanism, robust design, high efficiency, and reliability. However, the likelihood of faults cannot be overlooked, as the motors experience significant electrical and mechanical loads because of their prolonged working periods [1]. An intrinsic flaw in the machine or adverse surrounding conditions could be the reason for failure. If the initial erratic behaviour is not identified, it can lead to motor failure, which will result in downtime and increased operation loss. Rotating machine condition monitoring has thus become increasingly interesting to researchers due to the inherent vulnerability to damage and failure of these machines. In order to improve the accuracy and capabilities of fault diagnosis systems, researchers are currently analyzing weak fault signals to extract fault features and classify them to enable real-time monitoring and diagnosis [2]. It is important to diagnose and monitor faults accurately and in a timely manner to prevent significant damage, extend the life of machines, increase accessibility, and lessen maintenance costs [3].
Depending on the components, IM faults can be classified as bearing faults, faults connected to the rotor, faults connected to the stator, etc. Among them, approximately 44% of these faults occur in bearings [4,5][4][5]. In the case of bearing faults, the damage can occur in any of the four main components: the inner race, the outer race, the balls, and the cage. However, 90% of faults occur in the inner and outer races [6].
In attempts to avoid dangerous accidents due to electric motor failure, breakdown maintenance methods were initially replaced by time-based preventive maintenance techniques. These were performed in accordance with working time periods, regardless of whether the machine needed a maintenance checkup or not. This approach is not only expensive but causes an interruption in the continuous working flow. Therefore, non-invasive condition-based maintenance techniques are currently considered to be more effective because they can reduce the amount of unnecessary scheduled preventive maintenance operations and lower the operation cost [7]. Numerous studies have been conducted on bearing fault diagnosis to develop new advanced approaches by utilizing innovative technologies and industrial equipment. Model-based [8] and data-driven [9] approaches are two basic techniques utilized in fault diagnosis. Model-based methods require precise modelling of the dynamics of a system with a comparatively small dataset, which is crucial to design approaches for highly nonlinear and ambiguous circumstances. On the other hand, data-driven approaches have become popular as data acquisition processes have become easier due to improvements in advanced sensor technology. A data-driven approach requires less engineering and design effort, and it is possible to extract useful information about a system’s current condition using modern feature engineering techniques [10].
Various types of sensor data are available for bearing fault diagnosis, such as vibration signals, acoustic emission signals, current signals, stray flux, thermal images, etc. [11]. Vibration signal-based analysis is a popular approach because of its high sensitivity to bearing faults, which can transmit any sudden change of intrinsic information immediately. The main limitation of using this type of signal is the high cost and high maintenance requirements of vibration sensors [12]. Fault analysis using acoustic emissions can be effective for early fault detection with a low-energy signal, but it requires a high amount of data to provide a good result, which increases the computational complexity of the overall method [13]. Motor current signals have been used to effectively diagnose electrical faults (broken rotor bar faults, stator winding faults) and bearing faults. The acquisition of the current signal does not require any external sensors, which reduces the overall installation and data collection costs of the system.
Furthermore, current transducers can be used to measure the stator current from a single input source if frequency inverters and current transformers are not available. In addition to being highly reliable and noninvasive, motor current signal analysis (MCSA) is also considered one of the most effective conditions monitoring methods in bearing fault diagnosis [14,15,16][14][15][16]. MCSA has been applied to both to analyze bearing faults and the fault severity in IMs with fault frequency analysis [1,17][1][17].
Generally, the original signal acquired from sensors is not enough to spot the existence of a fault and classify fault conditions, due to the presence of surrounding noise. To avoid ambiguity, extracting effective features from the sensor data by applying signal processing techniques is essential. There are diverse techniques for feature extraction. In fault diagnosis, time-domain features such as the rms, peak-to-peak, root mean square, etc., are calculated using statistical formulas on the sensor signal; frequency-domain feature extraction involves fast Fourier transform, envelope analysis, and high-order spectral analysis of the time-series signal [18]; and time-frequency domain features are derived using the wavelet transform, short-time Fourier analysis, Hilbert–Huang transform, etc. [6,19][6][19]. Based on the processing gain and the ability to separate the fault characteristic frequency from the noise, frequency-domain analysis can provide a better understanding of fault frequencies than time-domain analysis. However, in many cases, methods based on the frequency domain do not perform well with nonstationary signals, whereas time-frequency-based methods can be an effective approach to deal with both stationary and nonstationary types of signals [20].
The main drawback of the Fourier transform-based feature extraction process is that it becomes unstable at high frequencies. In such cases, the wavelet transform is considered an effective signal processing technique for fault classification of the rotation machinery [21,22,23][21][22][23]. To create time shift, the discrete wavelet transform (DWT) and the second-generation wavelet transform (SGWT) perform splitting or downshifting operations, which result in erroneous output due to the aliasing effect, which hampers reflection on the original state of the system [24]. Another variant of the wavelet transform, named dual-tree complex wavelet transform (DT-CWT), reduces the aliasing effect due to its time shift invariance and parity sampling properties. Although the wavelet transform is stable for signal deformation, this approach is not translation invariant when subsampling is involved. For these reasons, the Fourier, as well as wavelet transforms, cannot be considered the ideal feature extractors.
Recently, a knowledge-based feature extraction technique has been developed by Bruna and Mallat named wavelet scattering transform (WST), which utilizes complex wavelets to balance the discrimination ability and stability of the time-frequency domain signal [25]. This method filters the signal by assembling a cascade of wavelet decomposition coefficients, complex moduli, and low-pass filtering operations. The WST approach enables the modulus and averaging operation of the wavelet coefficients to acquire stable features. After that, the cascaded wavelet transform is employed to recover the high-frequency information loss due to the previous wavelet coefficients’ averaging modulus operation. The resultant scattering coefficients possess local stability and translation invariance, and they have shown good performance in different application areas, such as image processing [26], sound classification [27], and heart sound classification [28]. The WST-based feature extraction process provides two advantages compared to other approaches in the fault diagnosis field. Firstly, the complex wavelet decompositions at multiple scales can provide rich descriptors of complicated structures for fault diagnosis through the co-occurrence of coefficients. Secondly, by using local weighted averaging, it is possible to reduce feature variability and preserve the local consistency of the class labels. It can also reduce the impact of noise originating from acquisition signals. Due to these reasons, researchers have become interested in this method and started implementing the WST in bearing and gearbox fault signal analysis. In [29], with the extracted scattering coefficients, a bearing fault was classified by SVM with 99% accuracy by utilizing vibration signals. Gearbox fault was analyzed in [30] with an acoustic emission signal by utilizing the WST with linear discriminant analysis (LDA); this approach had an affordable computational cost. Additionally, in [31], single and compound fault conditions were diagnosed by combining a denoising approach with WST coefficients to analyze rolling element bearings faults.
With the help of an effective feature extraction process, the original signal from sensors is transferred into a compact significant representation, which can be used as the input of machine learning classifiers for further training and optimizing decision functions. Common ML classifiers for fault diagnosis include support vector machine (SVM) [32], gradient boosting decision trees, k-nearest neighbours (KNN) [33], random forest (RF) [34[34][35],35], and neural network approaches [36,37][36][37]. Furthermore, deep learning (DL) methods have been implemented in multiple research areas, including bearing fault analysis and provide very good performance [38,39][38][39]. Recently, unsupervised cross-domain diagnosis based on a joint transfer network [40] and modified auxiliary classifier GAN (MACGAN) [41] were implemented to generate multi-mode fault samples where the fault samples are limited.
2. Wavelet Scattering Transform (WST)
A wavelet transform is a widely applied time-frequency analysis method that has the advantage of being stable and multi-scale in the presence of local deformation. It can effectively extract the local features from signals, but it is subject to change over time and can easily exclude significant signal features. A better time-frequency analysis technique built on the wavelet transform is the wavelet scattering transform (WST), which was proposed by Mallat [46][42]. The procedure is simply an iterative combination of a deep convolution network, consisting of low-pass filter averaging, a complex wavelet transform, and modulus operation [36]. With additional advantages of translation invariance, local deformation stability, and rich feature information representation, it also addresses the drawback of changing over time. For any given time-domain signal, x, the operation of WST can be described as follows:- 1.
-
At first, x is convolved with the dilated mother wavelet ψ, which has the center frequency of λ, to calculate the WST. This operation can be expressed as x*ψλ. Here, the average of the convolved signal, which oscillates at a scale of 2j, is zero.
- 2.
-
After that, a nonlinear operator, such as a modulus, is applied to the convolved signal to eliminate these oscillations (i.e., |x*ψλ|). This procedure is used to make up for the information lost due to downsampling by doubling the frequency of the given signal.
- 3.
-
Finally, a low-pass filter φ is applied to the resultant absolute convolved signal, which is equivalent to |x*ψλ|*φHere, S0x represents the zero-order scattering coefficients, which evaluate the local translation invariance of the given input signal. The high-frequency components of the convolved signal are lost during each stage’s averaging operation, but they can be recovered in the following stage’s convolution operation with the wavelet. The WST method possesses the stability of time warp deformation, conversion in energy, and contraction, which makes the overall system robust in a noisy environment and appropriate for many classification tasks [30]. As a result of implementing the low-pass filter, φ, the network is invariant to translations up to a certain invariance scale. The resultant features from Sx inherit properties of wavelet transforms, which make them stable against local deformations. This also allows the scattering decomposition to detect subtle changes in bearing signals’ amplitudes under different conditions and makes the classification task easier. Therefore, the wavelet scattering network can be used as an effective way to create robust representations of different bearing conditions that minimize the differences under the same condition and maintain enough discriminability to distinguish among different bearing conditions. Despite the similarity in structure between wavelet scattering networks and CNNs, there exist two main differences: the filters are predetermined rather than learned, and the features are not just the outputs of the final convolution layer but are all the layers combined. Based on previous research, nearly 99% of the scattering coefficient energy is contained within the first two layers of the scattering coefficient, with the energy decreasing rapidly as the layer level increases [25,47][25][43]. The WST applied in this woresearkch also considers scattering coefficients for two orders, which are represented as S1x and S2x. Through the cascaded wavelet decomposition, the WST can extract detailed feature information, and the local averaging technique can lessen the impact of noise. For these reasons, the WST can be considered a useful technique for extracting features in order to identify fault features in signals.
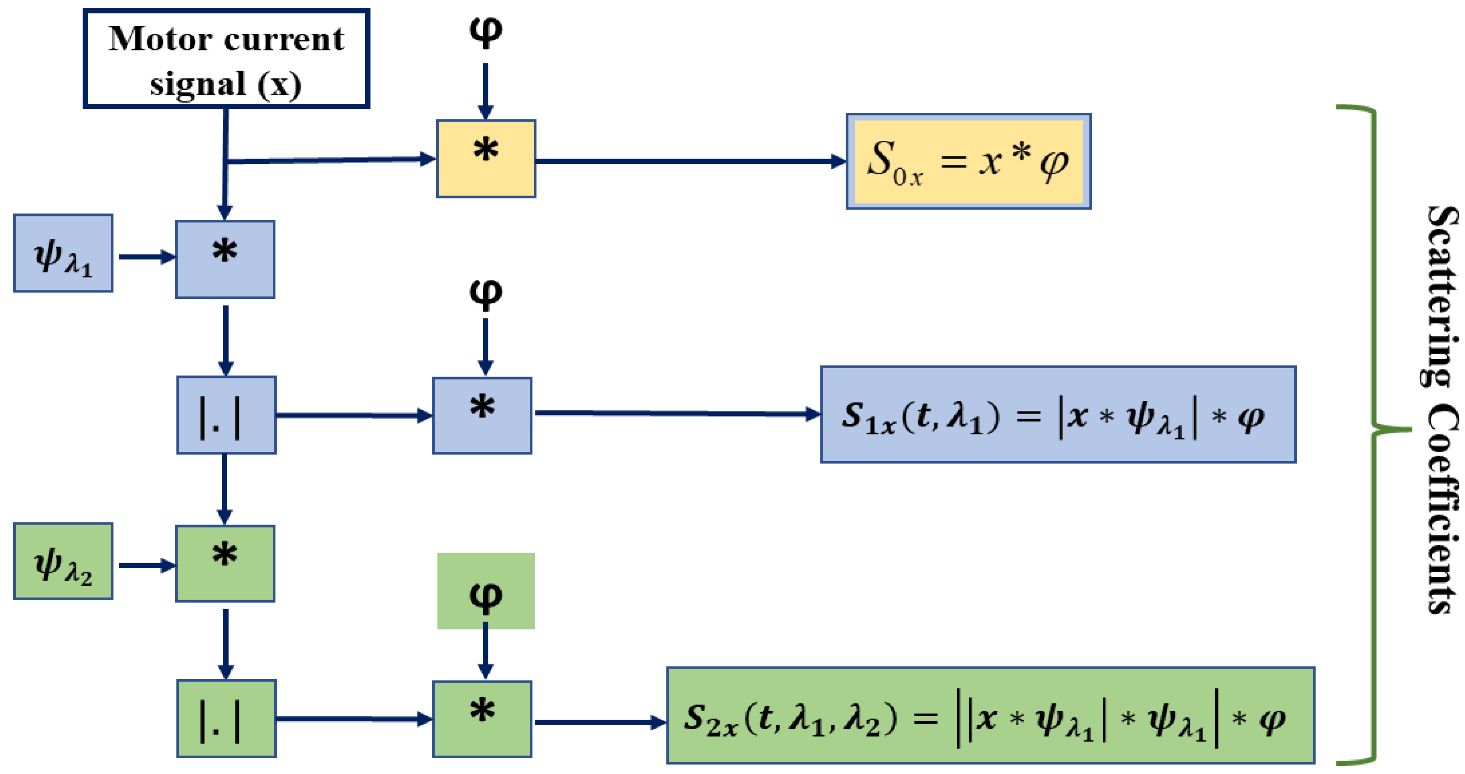 Figure 21.The schematic diagram of the feature extraction procedure with the second-order WST.
Figure 21.The schematic diagram of the feature extraction procedure with the second-order WST.
References
- Elbouchikhi, E.; Choqueuse, V.; Auger, F.; Benbouzid, M.E.H. Motor current signal analysis based on a matched subspace detector. IEEE Trans. Instrum. Meas. 2017, 66, 3260–3270.
- Ma, S.; Cheng, B.; Shang, Z.; Liu, G. Scattering transform and LSPTSVM based fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2018, 104, 155–170.
- Mehrjou, M.R.; Mariun, N.; Hamiruce Marhaban, M.; Misron, N. Rotor fault condition monitoring techniques for squirrel-cage induction machine—A review. Mech. Syst. Signal Process. 2011, 25, 2827–2848.
- Georgoulas, G.; Loutas, T.; Stylios, C.D.; Kostopoulos, V. Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition. Mech. Syst. Signal Process. 2013, 41, 510–525.
- Mboo, C.P.; Hameyer, K. Fault diagnosis of bearing damage by means of the linear discriminant analysis of stator current features from the frequency selection. IEEE Trans. Ind. Appl. 2016, 52, 3861–3868.
- Cerrada, M.; Sánchez, R.V.; Li, C.; Pacheco, F.; Cabrera, D.; Valente de Oliveira, J.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196.
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510.
- Martinez-Garcia, C.; Astorga-Zaragoza, C.; Puig, V.; Reyes-Reyes, J.; Lopez-Estrada, F. A Simple Nonlinear Observer for State and Unknown Input Estimation: DC Motor Applications. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 710–714.
- Maliuk, A.S.; Prosvirin, A.E.; Ahmad, Z.; Kim, C.H.; Kim, J.M. Novel bearing fault diagnosis using gaussian mixture model-based fault band selection. Sensors 2021, 21, 6579.
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581.
- Sarathee Bhowmik, P.; Pradhan, S.; Prakash, M. Fault Diagnostic and Monitoring Methods of Induction Motor: A Review. Int. J. Appl. Control. Electr. Electron. Eng. 2013, 1, 1–18.
- Immovilli, F.; Bianchini, C.; Cocconcelli, M.; Bellini, A.; Rubini, R. Bearing fault model for induction motor with externally induced vibration. IEEE Trans. Ind. Electron. 2013, 60, 3408–3418.
- Kim, J.Y.; Kim, J.M. Bearing fault diagnosis using grad-CAM and acoustic emission signals. Appl. Sci. 2020, 10, 2050.
- Giantomassi, A.; Ferracuti, F.; Iarlori, S.; Ippoliti, G.; Longhi, S. Electric motor fault detection and diagnosis by kernel density estimation and kullback-leibler divergence based on stator current measurements. IEEE Trans. Ind. Electron. 2015, 62, 1770–1780.
- Toma, R.N.; Prosvirin, A.E.; Kim, J.M. Bearing fault diagnosis of induction motors using a genetic algorithm and machine learning classifiers. Sensors 2020, 20, 1884.
- Toma, R.N.; Piltan, F.; Kim, J.M. A deep autoencoder-based convolution neural network framework for bearing fault classification in induction motors. Sensors 2021, 21, 8453.
- Martinez-Montes, E.; Jimenez-Chillaron, L.; Gilabert-Marzal, J.; Antonino-Daviu, J.; Quijano-Lopez, A. Evaluation of the Detectability of Bearing Faults at Different Load Levels Through the Analysis of Stator Currents. In Proceedings of the 2018 23rd International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 25 October 2018; pp. 1855–1860.
- Nikravesh, S.M.Y.; Nezamivand Chegini, S. Crack identification in double-cracked plates using wavelet analysis. Meccanica 2013, 48, 2075–2098.
- Pothisarn, C.; Klomjit, J.; Ngaopitakkul, A.; Jettanasen, C.; Asfani, D.A.; Negara, I.M.Y. Comparison of various mother wavelets for fault classification in electrical systems. Appl. Sci. 2020, 10, 1203.
- Tian, J.; Morillo, C.; Azarian, M.H.; Pecht, M. Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled with K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2016, 63, 1793–1803.
- Teng, W.; Ding, X.; Zhang, X.; Liu, Y.; Ma, Z. Multi-fault detection and failure analysis of wind turbine gearbox using complex wavelet transform. Renew. Energy 2016, 93, 591–598.
- Lu, W.; Jiang, W.; Yuan, G.; Yan, L. A gearbox fault diagnosis scheme based on near-field acoustic holography and spatial distribution features of sound field. J. Sound Vib. 2013, 332, 2593–2610.
- Toma, R.N.; Kim, J.M. Bearing fault classification of induction motors using discrete wavelet transform and ensemble machine learning algorithms. Appl. Sci. 2020, 10, 5251.
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15.
- Bruna, J.; Mallat, S. Invariant scattering convolution networks. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1872–1886.
- Leonarduzzi, R.; Liu, H.; Wang, Y. Scattering transform and sparse linear classifiers for art authentication. Signal Process. 2018, 150, 11–19.
- Souli, S.; Lachiri, Z. Audio sounds classification using scattering features and support vectors machines for medical surveillance. Appl. Acoust. 2018, 130, 270–282.
- Li, J.; Ke, L.; Du, Q.; Ding, X.; Chen, X.; Wang, D. Heart Sound Signal Classification Algorithm: A Combination of Wavelet Scattering Transform and Twin Support Vector Machine. IEEE Access 2019, 7, 179339–179348.
- Ambika, P.S.; Rajendrakumar, P.K.; Ramchand, R. Vibration signal based condition monitoring of mechanical equipment with scattering transform. J. Mech. Sci. Technol. 2019, 33, 3095–3103.
- Heydarzadeh, M.; Nourani, M.; Hansen, J.; Hedayati Kia, S. Non-invasive gearbox fault diagnosis using scattering transform of acoustic emission. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing—Proceedings, New Orleans, LA, USA, 5–9 March 2017; pp. 371–375.
- Guo, J.; Si, Z.; Xiang, J. A compound fault diagnosis method of rolling bearing based on wavelet scattering transform and improved soft threshold denoising algorithm. Meas. J. Int. Meas. Confed. 2022, 196, 111276.
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing health monitoring based on hilbert-huang transform, support vector machine, and regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62.
- Wang, D. K-nearest neighbors based methods for identification of different gear crack levels under different motor speeds and loads: Revisited. Mech. Syst. Signal Process. 2016, 70–71, 201–208.
- Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Huang, B.; Si, Y. A Data-Driven Design for Fault Detection of Wind Turbines Using Random Forests and XGboost. IEEE Access 2018, 6, 21020–21031.
- Cerrada, M.; Zurita, G.; Cabrera, D.; Sánchez, R.V.; Artés, M.; Li, C. Fault diagnosis in spur gears based on genetic algorithm and random forest. Mech. Syst. Signal Process. 2016, 70–71, 87–103.
- Andén, J.; Mallat, S. Deep scattering spectrum. IEEE Trans. Signal Process. 2014, 62, 4114–4128.
- Toma, R.N.; Kim, J.M. Bearing Fault Classification of Induction Motor Using Statistical Features and Machine Learning Algorithms. Lect. Notes Netw. Syst. 2022, 418 LNNS, 243–254.
- Pham, M.T.; Kim, J.M.; Kim, C.H. Efficient fault diagnosis of rolling bearings using neural network architecture search and sharing weights. IEEE Access 2021, 9, 98800–98811.
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnosticsx—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881.
- Xiao, Y.; Shao, H.; Han, S.Y.; Huo, Z.; Wan, J. Novel Joint Transfer Network for Unsupervised Bearing Fault Diagnosis From Simulation Domain to Experimental Domain. IEEE/ASME Trans. Mechatron. 2022, 1–10.
- Li, W.; Zhong, X.; Shao, H.; Cai, B.; Yang, X. Multi-mode data augmentation and fault diagnosis of rotating machinery using modified ACGAN designed with new framework. Adv. Eng. Inform. 2022, 52, 101552.
- Mallat, S. Group Invariant Scattering. Commun. Pure Appl. Math. 2012, 65, 1331–1398.
- Andén, J.; Mallat, S. Multiscale scattering for audio classification. In Proceedings of the International Society for Music Information Retrieval Conference ISMIR, Miami, FL, USA, 24–28 October 2011; pp. 657–662.
More
