External cavity semiconductor lasers (ECSLs) usually refer to the gain chip based on the introduction of external optical components (such as waveguides, gratings, prisms, etc.) to provide optical feedback. By designing the type, position and structure of external optical components, the optical properties of SLs (such as center wavelength, linewidth, tuning range, side-mode suppression ratio (SMSR), etc.) can be changed. Bragg grating external cavity semiconductor laser (BG-ECSL) is a device with a specific optical element (Bragg grating) in the external cavity. BG-ECSLs have excellent performances, such as narrow linewidth, tunability and high SMSR. They are widely used in WDM systems, coherent optical communication, gas detection, Lidar, atomic physics and other fields.
- tunable
- narrow linewidth
- Bragg grating
- BG-ECSL
1. Principle of Bragg Grating External Cavity Semiconductor Lasers (BG-ECSLs)

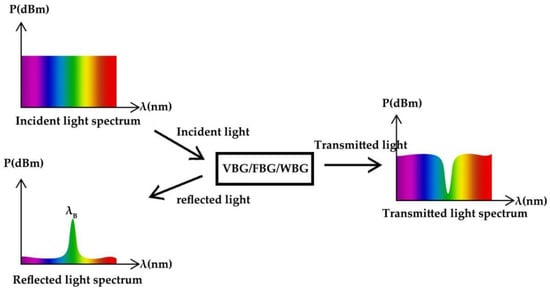
2. Research Progress of BG-ECSLs
The structures of BG-ECSLs can be mainly divided into the VBG structure, FBG structure and WBG structure. This research mainly discusses the research progress of VBG structure, FBG structure and WBG structure of BG-ECSLs. BG-ECSLs have a long history. Since the 1970s, in order to make Bragg grating in fiber and other materials, people have carried out a lot of research on the effect of UV radiation damage in silica, germanium-doped silicon glass and other materials. Nowadays, there are many kinds of Bragg grating, and the application fields are also very wide. Due to the unique characteristics and potential application prospects of Bragg grating, since the first batch of BG-ECSLs came out, a large number of companies have studied and continuously optimized the performance of BG-ECSLs. At present, Coherent, OptiGrate, DILAS and so on are well-known in the world. Among them, the United States, Germany, France, Sweden, Canada, Japan and other countries have certain technical advantages in the development of BG-ECSLs. In China, there are also a large number of companies and research institutions developing relevant cutting-edge technologies, such as Wuhan National Laboratory of Optoelectronics, Shanghai Institute of Optics and Precision Instruments, Chinese Academy of Sciences, Beijing Institute of Semiconductors, Chinese Academy of Sciences, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, etc. BG-ECSLs can be widely used in optical communication, biotechnology, environmental detection, material processing and other fields and has potential application prospects in high-precision detection, quantum communication system and other fields.3. Applications
BG-ECSLs can be widely used in optical communication, gas detection, coherent light detection, synthetic aperture Lidar, spectral gas sensing and other fields and has potential application prospects in underwater optical communication, spaceborne carbon dioxide detection Lidar, biomedical imaging system, high-speed long-distance quantum communication system, etc. [1][2][3]. In this research, the principle of BG-ECSLs is described, and the research achievements and latest progress in this field in the past ten years are reviewed. As shown in Table 1, the linewidth of VBG-ECSLs is in the range of kHz-THz (generally in the order of kHz-GHz), the SMSR is in the range of 16~57 dB and the tuning range is in the order of GHz (most of them are tens of picometers). The narrowest linewidth can be as low as 2 kHz while having SMSR up to 57 dB, but the continuous tunable range is small, only 0.063 nm. The maximum tuning range is 1.9 nm. The linewidth of FBG-ECSLs is in the range of kHz~GHz and that of SMSR is in the range of 25~82 dB. The tuning range is in the order of GHz and THz (from tens of picometers to tens of nanometers, and the tuning range is better than that of VBG-ECSLs). The narrowest linewidth can be as low as 125 Hz while having a continuous tunable range of 0.8nm. The maximum SMSR is 82 dB with a narrow linewidth of 16 kHz. The maximum continuous tuning range is 48 nm. The linewidth of WBG-ECSLs is in the range of KHz~GHz, and that of SMSR is in the range of 15~82 dB. The tuning range is in the order of GHz and THz (from hundreds of picometers to tens of nanometers, the tuning range is better than FBG-ECSLs). The narrowest linewidth can be as low as 320 Hz, and the SMSR can be greater than 55 dB. The maximum SMSR is greater than 60 dB, and the linewidth is less than 17 kHz, which can be continuously tuned to 20.2 GHz. The maximum tuning range is 81.8 nm. From the characteristics of commercial BG-ECSLs products, it is not difficult to find that VBG-ECSLs can obtain relatively large output power, while FBG-ECSLs and WBG-ECSLs can obtain a relatively wide tuning range, and the tuning range of WBG-ECSLs is larger, because commercial products are highly targeted (most of them are aimed at a certain module in a certain application or even a certain band). In order to meet the parameter requirements of their application field, most companies do not pursue performances with a low parameter impact on the field. For the application of DWDM, the company pursues parameters such as tuning range, linewidth, output power, SMSR, etc. when conducting research on commercial products, but some parameters cannot obtain the optimal values at the same time. For example, according to Formula (2), if the linewidth is narrower, the output power will be lower. Therefore, in the design of products, it is necessary to meet the requirements of the primary parameters (tuning range), combined with the existing technology, comprehensive consideration of production costs, product stability and other factors to adopt the optimal choice.| Type | VBG | FBG | WBG |
|---|---|---|---|
| Main Materials | Photo-Thermo-Refractive, Polymer | Glass, Crystal, Plastomer | Si, SiO2, Si3N4, LiNbO3, Polymer |
| Linewidth Range | 2 kHz~1.5 THz | 125 Hz~312 GHz | 320 Hz~85.3 GHz |
| Min linewidth | 2 kHz | 125 Hz | 320 Hz |
| SMSR Range | 16 dB~57 dB | 15 dB~82 dB | 15 dB~60 dB |
| Max SMSR | 57 dB | 82 dB | 60 dB |
| Tuning Range | 0.011 nm~2 nm | 0.1 nm~85 nm | 0.16 nm~100 nm |
| Max Tuning Range | 2 nm | 85 nm | 100 nm |
| Output Power | 10 mW~106.4 W | 0.05 mW~670 mW | 0.5 mW~312 mW |
| Maximum Output Power | 106.4 W | 670 mW | 312 mW |
References
- Saktioto, T.; Fadilla, F.D.; Soerbakti, Y.; Irawan, D.; Okfalisa. Application of Fiber Bragg Grating Sensor System for Simulation Detection of the Heart Rate. J. Phys. Conf. Ser. 2021, 2049, 012002.
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Advances in Waveguide Bragg Grating Structures, Platforms, and Applications: An Up-to-Date Appraisal. Biosensors 2022, 12, 497.
- Jinachandran, S.; Rajan, G. Fibre Bragg grating based acoustic emission measurement system for structural health monitoring applications. Materials 2021, 14, 897.
- Park, T.H.; Kim, S.M.; Oh, M.C. Polymer-waveguide Bragg-grating devices fabricated using phase-mask lithography. Curr. Opt. Photonics 2019, 3, 401–407.
- Nishijima, Y.; Ueno, K.; Juodkazis, S.; Mizeikis, V.; Fujiwara, H.; Sasaki, K.; Misawa, H. Lasing with well-defined cavity modes in dye-infiltrated silica inverse opals. Opt. Express 2009, 17, 2976–2983.
- Zheng, Y.; Yue, J.; Zhang, P. Analysis of parameter influence law of waveguide Bragg grating. Opt. Laser Technol. 2022, 146, 107576.
- Mikutis, M.; Kudrius, T.; Šlekys, G.; Paipulas, D.; Juodkazis, S. High 90% efficiency Bragg gratings formed in fused silica by femtosecond Gauss-Bessel laser beams. Opt. Mater. Express 2013, 3, 1862–1871.
- Roth, G.L.; Kefer, S.; Hessler, S.; Esen, C.; Hellmann, R. Polymer photonic crystal waveguides generated by femtosecond laser. Laser Photonics Rev. 2021, 15, 2100215.
