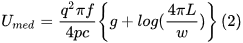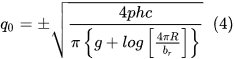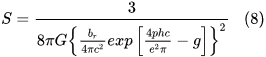Classical electrodynamics was introduced by James Clear Maxwell nearly 150 years ago and it is a subject that had been thoroughly explored over these years. Notwithstanding this long term scrutiny of this subject, there are hidden features in classical electrodynamics that actually heralds the emergence of Quantum electrodynamics in the future. Such examples can be found when analyzing the electromagnetic radiation generated by antennas working in both frequency and time domain and in the case of transition radiation generated by decelerating electrons. Here we discuss one such case. Consider the radiation generated by an antenna working in frequency domain. One can show that the energy dissipated as radiation within half a period of oscillation, say U, satisfies the inequality U ≥ hf →q ≥ e where q is the magnitude of the oscillating charge in the antenna, e is the elementary charge, f is the frequency of oscillation and h is the Planck constant. This result is derived while adhering strictly to the principles of classical electrodynamics alone. Combining this result with the concept of photons burrowed from quantum mechanics, one can derive an expression for the elementary charge as a function of other natural constants and the energy density of vacuum. The expression predicts the value of elementary charge to an accuracy higher than about 0.1%.
- Classical Electrodynamics
- Elementary charge
- Vacuum Energy
- Dark Energy
- Hubble Radius
- Electronic charge
1. Introduction
Classical electrodynamics is a classical field theory. The quantum version of this theory is the quantum electrodynamics. However, recent studies based on classical electromagnetic theory shows that there are several indications in this classical field theory that herald the future emergence of quantum electrodynamics. One can find such cases while analyzing the radiation generated by both frequency and time domain antennas and the transition radiation generated by decelerating electrons[1][2]. In this note we will concentrate only on the radiation from frequency domain antennas excited by oscillating currents. One can find the references pertinent to time domain and transition radiation also in reference [1].
2. Theory and results
As the radiating system consider a lossless transmitting antenna working in frequency domain located over a perfectly conducting ground plane. The antenna together with the ground plane acts as a center fed transmitting dipole. The length of the antenna is L, the radius of the antenna is r, the frequency of oscillation of the current or charge in the antenna is f , w is the corresponding wavelength and T is the period of oscillation. The power dissipated by this antenna, excited by an oscillating current, takes place in energy bursts with duration equal to half the period, i.e. T/2. This paper is concerned with the energy dissipated within such a single burst. The material to be given below is adapted from references [1] and [2].
As the value of L/w increases, the energy dissipated by this antenna over a period of T/2 oscillates around a median value. This median energy denoted by Umed is given by

In Equation (1), g is Euler’s constant, which is equal to 0.5772, p is the permittivity of free space, and q is the magnitude of the oscillating charge. For a given charge q , the median energy increases with increasing length of the antenna and decreasing wavelength. Therefore the median value of the energy increases with increasing ratio L/w. Note that for a given L This ratio increases with decreasing wavelength. To maximize the energy output of the antenna let us work with the smallest possible wavelength that can be accommodated by the theory that led to Equation 1. Since the above equation is valid when the wavelength is in the order of or larger than the radius of the antenna r, let us replace w with r in Equation 1. With this slight change, Equation 1 can be written as
As mentioned earlier, the median energy increases with increasing ratio L/r. Now, the smallest radius of the antenna that we can find in nature cannot be smaller than the atomic dimensions. We can represent the atomic dimension by the Bohr radius. Let us denote the Bohr radius by br. The largest possible value of the length of the antenna is given by the size of the universe. Actually, by the size of the universe we mean the region of the universe that is in causal contact with the observer. The outer boundary of this region is determined by the Hubble radius. Thus the maximum length of the antenna that can be accommodated within the universe is equal to the Hubble radius. However, the Hubble radius increases with time and the maximum length of the antenna ever possible is determined by the ultimate or the steady state value of the Hubble radius. Let us denote this steady state value by R. Thus, the maximum value of the ratio L/r ever possible in the current universe is given by R/br. Let us denote such an antenna as the 'ultimate antenna'. Note that ultimate antenna is a hypothetical antenna; it can never be realized in practice, and its radiating efficiency surpasses any other antenna in the universe. That is, for a given oscillating charge no other antenna in the universe can generate, over a given period of time, as much energy as the ultimate antenna. The energy radiated by the ultimate antenna over a period of T/2 is given by
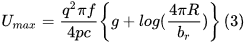
One can observe that this energy depends on the magnitude of the oscillating charge in the antenna. Let us now estimate the magnitude of the charge needed in the antenna so that Umax=hf where h is the Planck constant. Of course, hf is the energy associated with a single photon of frequency f. This charge denoted here by q0 is given by
In order to estimate the value of q0 we need to plug in the value of R into above equation. Theory of cosmology states that the value of R is determined by the energy density of the vacuum. The connection between these two parameters is given by
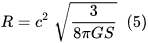
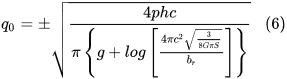
In the above equation, G is the gravitational constant and S is the energy density of the vacuum. Substituting the expression for R in equation 4 we obtain
Substituting numerical values for the variables together with the experimentally observed value of the energy density of the vacuum of about about 6×10-10 J/m3 into equation 6 we obtain q0=1.603×10-19 C. This value is equal to the elementary charge to an accuracy of about 0.1%. This shows that when the magnitude of the oscillating charge in the ultimate antenna is equal to the charge of an electron, the energy dissipated over a single burst of radiation of the antenna becomes equal to the energy of a photon. Now, recall that the ultimate antenna is the most efficient antenna that one can have in the universe, any other antenna will need a charge larger than the elementary charge to make the energy associated with a single burst of energy to be equal to that of a photon. The same is true if we include the losses pertinent to current propagation along the antenna. These losses will reduce the radiated energy for a given charge and, therefore, more charge is needed than the lossless case to reach the same level of energy dissipation. Thus we can write down the following universal condition which is valid for all the antennas: U ≥ hf →q ≥ e where q is the magnitude of the oscillating charge in the antenna, e is the elementary charge, f is the frequency of oscillation and h is the Planck constant. Note however that the reverse of this condition, namely, q ≥ e →U ≥ hf is not true because q ≥ e does not necessarily leads to U ≥ hf.
Note that up to this point we have not deviated from classical electrodynamics and the above relationship is a consequence of this classical theory.
3. Discussion
Let us look at the universal condition derived in the previous section, namely, U ≥ hf →q ≥ e. Consider the left hand side of this relationship. Classical electrodynamics does not place any restrictions on the amount of energy that can be generated in a single burst of radiation. That is, U can take any small value in classical electrodynamics. In other words, according to classical electrodynamics there is no reason for U to be larger than hf. However, we k,now from quantum mechanics that the energy dissipated in a single burst of radiation cannot be smaller than that of a photon. Thus, only by appealing to quantum mechanics we can ascertain that U ≥ hf is a correct and valid statement. Therefore, by appealing to quantum mechanics we can also state q ≥ e. That is the free charge available in nature has to be equal to or larger than that of an electron.
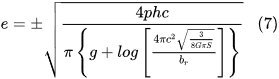
Equation 6 is derived using pure classical electrodynamics and it indicates that q0 is almost equal to the elementary charge. If we assume that q0 is exactly equal to the elementary charge, then, Equation 6 can be written as
As explained in reference [1], Note that even though Equations 6 and 7 are almost equivalent they are based on very different assumptions. In Equation 6, q0 is the charge necessary in the ultimate antenna so that the median energy dissipated over half a period, T/2 , is equal to hf . This is a result based purely on classical electrodynamics. The value of q0 is almost equal to the elementary charge (to an accuracy less than 1%) and we assume that q0 = e. However, the condition q0 = e is valid only if the value of U does not go below hf . But, classical electrodynamics does not place any restrictions on the value of U and accordingly, it can take any value larger than zero. The statement q0 = e is based, therefore, on quantum nature of the electromagnetic radiation. Thus, Equation 7 is a result of the fact that electromagnetic radiation consists of photons.
Equation 7 can be rewritten while making S the subject as
Equation 8 is an expression for the energy density of vacuum in terms of well-known physical constants. If we substitute numerical values to these constants, we find S =4×10-10 J/m3 which is close to the measured value 6×10-10 J/m3. Indeed, S =4×10-10 J/m3 is the value we need in Equation 6 to make q0 = e . Equation 8 can be considered as an alternative expression for the vacuum energy density.
In a glance, it is difficult to understand how the charge of an electron and the size of the steady state (or the ultimate) Hubble radius, as indicated by Equations 6, 7 and 8, are connected. We believe that the relationship between the size of the universe and the elementary charge is a secondary relationship. As per Equations 6 and 7, the true primary connection is probably associated with the energy density of the vacuum and the elementary charge. Observe also that if S=0 then R=∞ and the value of the elementary charge goes to zero. This seems to indicate that the vacuum energy is an essential feature for the existence of electric charge.
4. Conclusion
All radiating systems that generate frequency domain radiation satisfy the condition U ≥ hf →q ≥ e where U is the energy dissipated within the time T/2. By combining this result with the concept that electromagnetic radiation is a stream of photons, it is possible to show that the elementary charge and the vacuum energy are intimately connected.
References
- Cooray, Vernon; Cooray, Gerald; Novel Features of Classical Electrodynamics and Their Connection to the Elementary Charge, Energy Density of Vacuum and Heisenberg’s Uncertainty Principle—Review and Consolidation . Journal of modern physics 2019, 10, No 1, 74 - 90, DOI: 10.4236/jmp.2019.101007.
- Cooray, Vernon; Cooray, Gerald; Remarkable Predictions of Classical Electrodynamics on Elementary Charge and the Energy Density of Vacuum. Journal of Electromagnetic Analysis and Applications 2018, 10, 77-87, doi: 10.4236/jemaa.2018.105006.