The transversely isotropic media with a vertical axis of symmetry (VTI media) has been the most popular model for the sedimentary rocks in the interior of the earth. These rocks are usually isotropic within a given layer but strongly anisotropic from layer to layer. Reflection and refraction of acoustic waves between the adjacent rock layers have profound implications in geophysical applications. We discuss some anomalous reflection phenomena of the acoustic wave at the interface between the layered anisotropic rock media.
- Anomalous refraction
- VTI medium
- TTI medium,
- anisotropic media interface,
- anomalous incident angle,
- acoustic-logging,
- analysis of seismic signal
1. Introduction
Sedimentary rocks in the interior of the earth are usually considered in a sequence of thin layers. The physical properties, such as acoustic impedance, are commonly treated as invariant within a layer but can vary from layer to layer. Therefore, the layered rocks are preserved as transversely isotropic with respect to its vertical axis of symmetry but macroscopically anisotropic [1][2][3][4][1-4]. Reflection and refraction of acoustic waves between adjacent rocks have profound implications in geophysics, e.g., in earthquake seismology, seismic image and analysis, and underwater acoustics [5][6][7][8][9][10][11][5-11]. The physical properties of the transversely isotropic media with a vertical axis of symmetry (VTI media), as shown in Figure 1(a), can be described by an elastic stiffness tensor [2][7][12][13][14][15][16][2, 7, 12-16],
 , (1)
, (1)
where the matrix elements are functions of stress and strain in the medium and c12 =c11 - 2c66.
The reflection and refraction coefficients are influenced by several factors, including the acoustic-impedance, the anisotropy of the media at two sides of the interface, and the incident angle of the acoustic signal. The critical incident angles are also affected by the anisotropy.
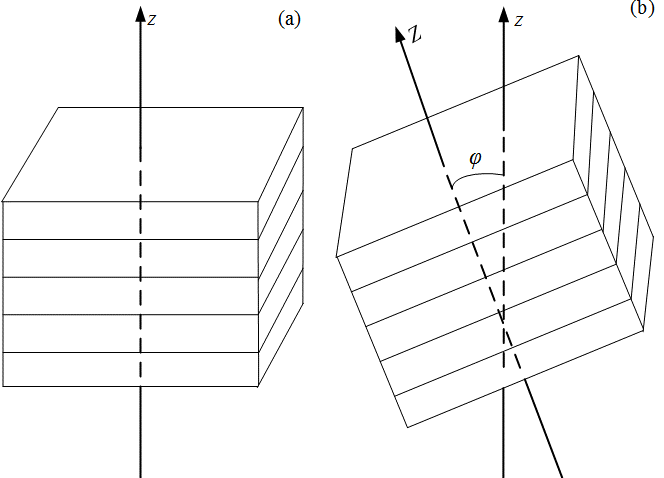
Figure 1. A schematic representation of the sedimentary rock layers: (a) a transversely isotropic medium with a vertical axis of symmetry (VTI medium), (b) a transversely isotropic medium with a tilt axis of symmetry (TTI medium) [17][Ref. 22].
At the interface between two VTI media, as shown in Figure 2, Snell’s law can be used to establish a fourth-order polynomial for the angles of the reflection and refraction [13]. Most recently, an eighth-order polynomial has also been established for the transversely isotropic medium with a tilt axis of symmetry (TTI medium), as shown in Figure 1(b) [17][22]. The solution reveals a possible anomalous incident angle that occurs for strongly anisotropic media.
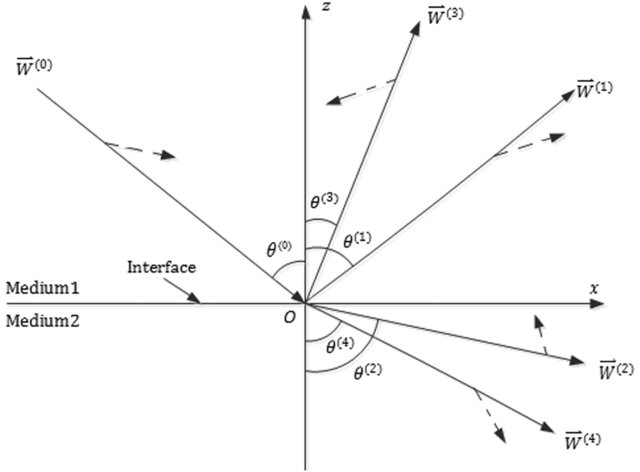
Figure 2. A schematic representation of reflection and refraction of acoustic waves at the VTI-VTI interface, where the solid lines with arrowheads indicate the phase velocity directions and the dashed lines with arrowheads show the polarization directions. W(m) is a particle displacement, and the index m denotes the incident P-wave (m = 0), reflected P-wave (m = 1), refracted (m = 2) P-wave, reflected SV-wave (m = 3), and refracted SV-wave (m = 4) respectively [18][Ref. 20].
2. Anomalous Incident Angle
The angles of reflection and refraction are defined in Figure 2. The anomalous incident angle is usually in the post-critical incidence region. The phase velocities are given as 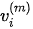 . The reflection and refraction are defined such that R(1) is the reflection coefficient of P-wave to P-wave, R(2) is the refraction coefficient of P-wave to P-wave, R(3) is the reflection coefficient of P-wave to SV-wave, and R(4) is the refraction coefficient of P-wave to SV-wave. Finally,
. The reflection and refraction are defined such that R(1) is the reflection coefficient of P-wave to P-wave, R(2) is the refraction coefficient of P-wave to P-wave, R(3) is the reflection coefficient of P-wave to SV-wave, and R(4) is the refraction coefficient of P-wave to SV-wave. Finally, 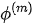 is a phase shift for an induced wave relative to the incident P-wave.
is a phase shift for an induced wave relative to the incident P-wave.
The physical origin of the anomalous reflection is the strong anisotropy of the media, embedded in Snell’s law. For any given incident angle regime, all waves involved in the reflection and refraction must satisfy Snell’s law (see Figure 2),
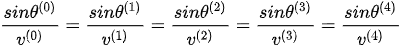 . (2)
. (2)
For some specific incident angle, the required root of the phase velocities of the refracted P-wave must be adjusted in order to satisfy Snell’s law, 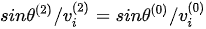 , where
, where 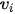 (i = 1, 2) are the two phase-velocity solutions.
(i = 1, 2) are the two phase-velocity solutions.
As an example, let’s consider the interface between two sedimentary rocks, specifically, anisotropic shale (A-shale) as the incidence medium and oil shale (O-shale) as the refraction medium. The physical properties of these sedimentary rocks have been reported in the literature [19][20][21][17-19], from which the angles of reflection and refraction may be calculated based on a fourth-order polynomial [13][19][20][21][13, 17-19]. Figure 3 shows the angle of the refracted P-wave as a function of the incident angle. Figure 4 presents the velocity of the refracted P-wave as a function of the incident angle.
Figures 3-4 show that for the interface of A-shale and O-shale, there is indeed an anomalous incident angle found at θ = 62.04o. This anomalous incident angle is at the post-critical angle region corresponding to the refracted P-wave.
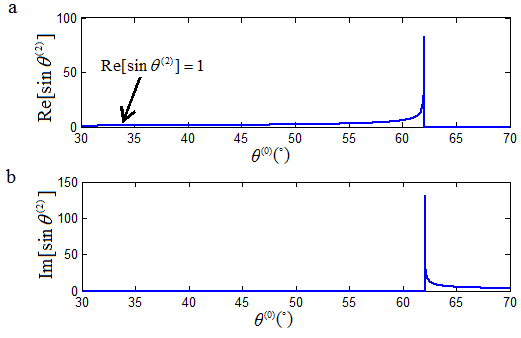
Figure 3. The angle of the refracted P-wave as a function of the incident angle at the interface of A-shale and O-shale, showing an anomalous incident angle at 62.04o [18][Ref. 20].
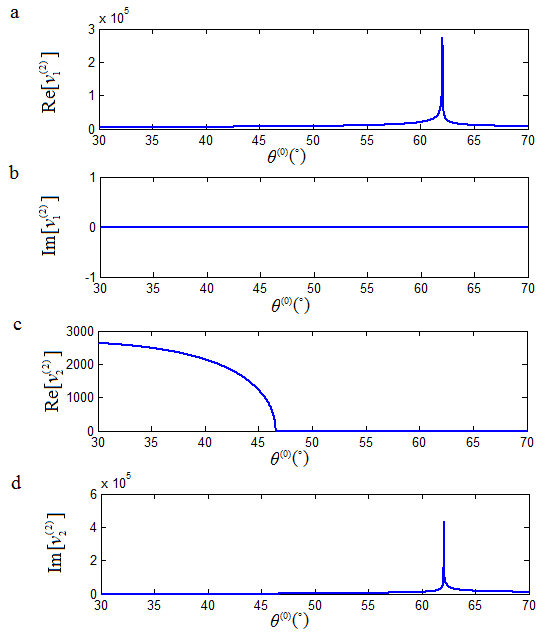
Figure 4. The velocity of the refracted P-wave as a function of the incident angle at the interface of A-shale and O-shale, showing an anomalous incident angle at 62.04o [18][Ref. 20].
3.
Anomalous Refraction
For the calculated results at the incident angle of 62.04o as shown in Figure 4, the phase velocity solution of the refracted P-wave is different before and after this incident angle, switching from 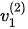 to
to 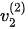 . The switching of the phase velocity solutions at this incident angle avoids a step variation of the calculated reflection and refraction coefficients that must abide by the law of energy conservation. This justification of the phase velocity from
. The switching of the phase velocity solutions at this incident angle avoids a step variation of the calculated reflection and refraction coefficients that must abide by the law of energy conservation. This justification of the phase velocity from 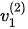 to
to 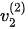 is anomalous for the P-wave to P-wave refraction.
is anomalous for the P-wave to P-wave refraction.
As an example, consider the P-wave to P-wave refraction coefficient R(2). For the interface of O-shale and A-shale, the refraction coefficient, as a function of incident angle, is presented in Figure 5. Similar results have been found for the reflection and refraction of P-wave to SV-waves.
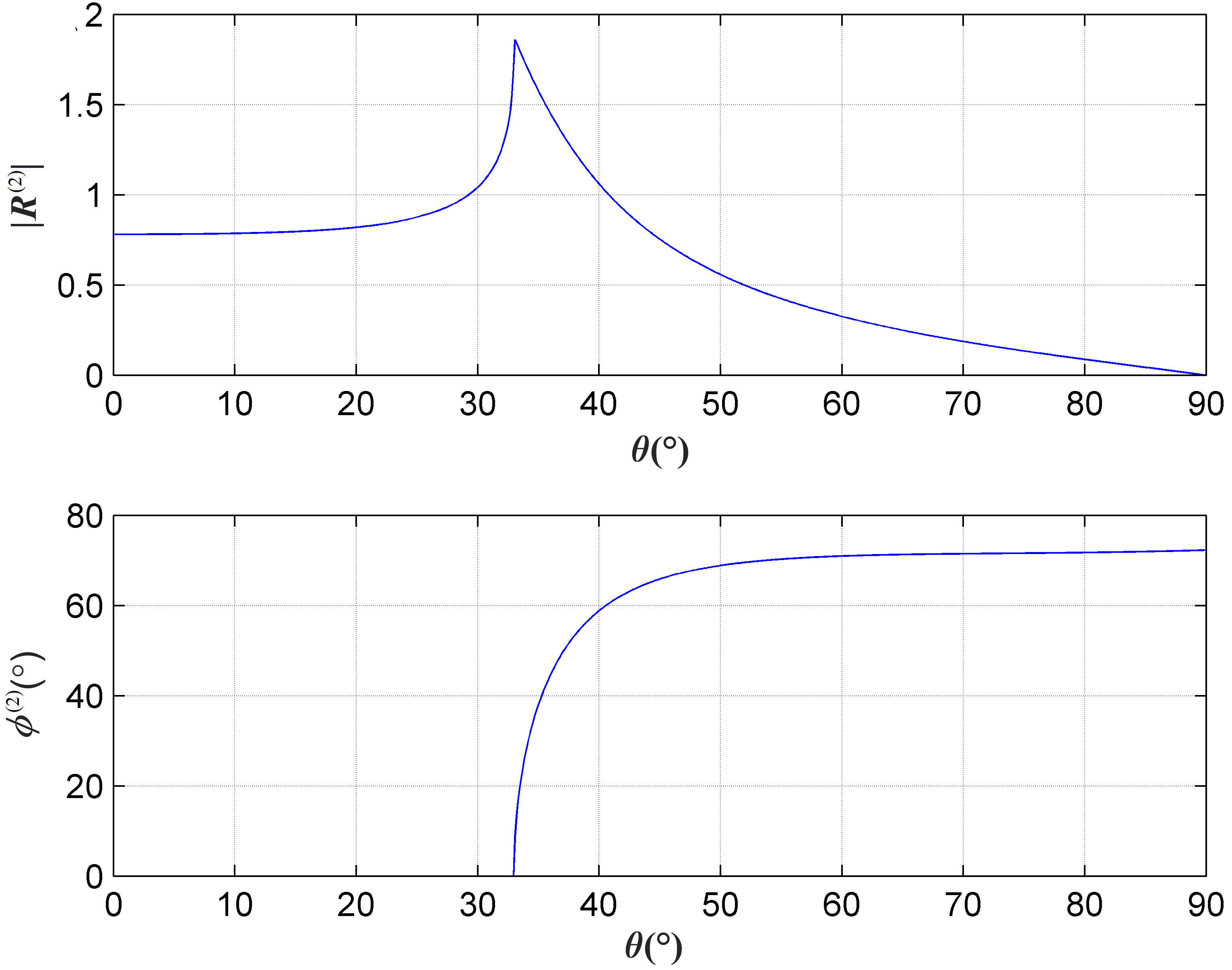
Figure 5. The refraction coefficient as a function of incident angle for the interface between A-shale and O-shale [20][Ref. 18]: (a) amplitude of the reflection coefficient, (b) phase angle.
It is noted that in the case of an anisotropic interface, the incident critical angle of the refracted P-wave is at 40.45°, e.g., in the weak anisotropic interface of A-shale and T-sandstone. In a strong anisotropic interface such as the interface of A-shale and O-shale, an anomalous incident angle is at 62.04° in the post-incident angle region. This corresponds to a critical angle of 33.63° for the refracted P-wave. At this critical angle of incidence, discontinuities in the reflection and refraction coefficients occur, as shown in Figure 5.
In such an abnormal angle of incidence, the solution of the phase velocity of the refracted P-wave must be adjusted, so that the solution of the phase velocity satisfies Snell's law. This guarantees that the calculated reflection and refraction coefficients are continuous at this anomalous incident-angle.
For the interface between A-shale and O-shale, the calculated reflection and refraction coefficients as functions of media anisotropy and incident-angle are given in Figure 6.
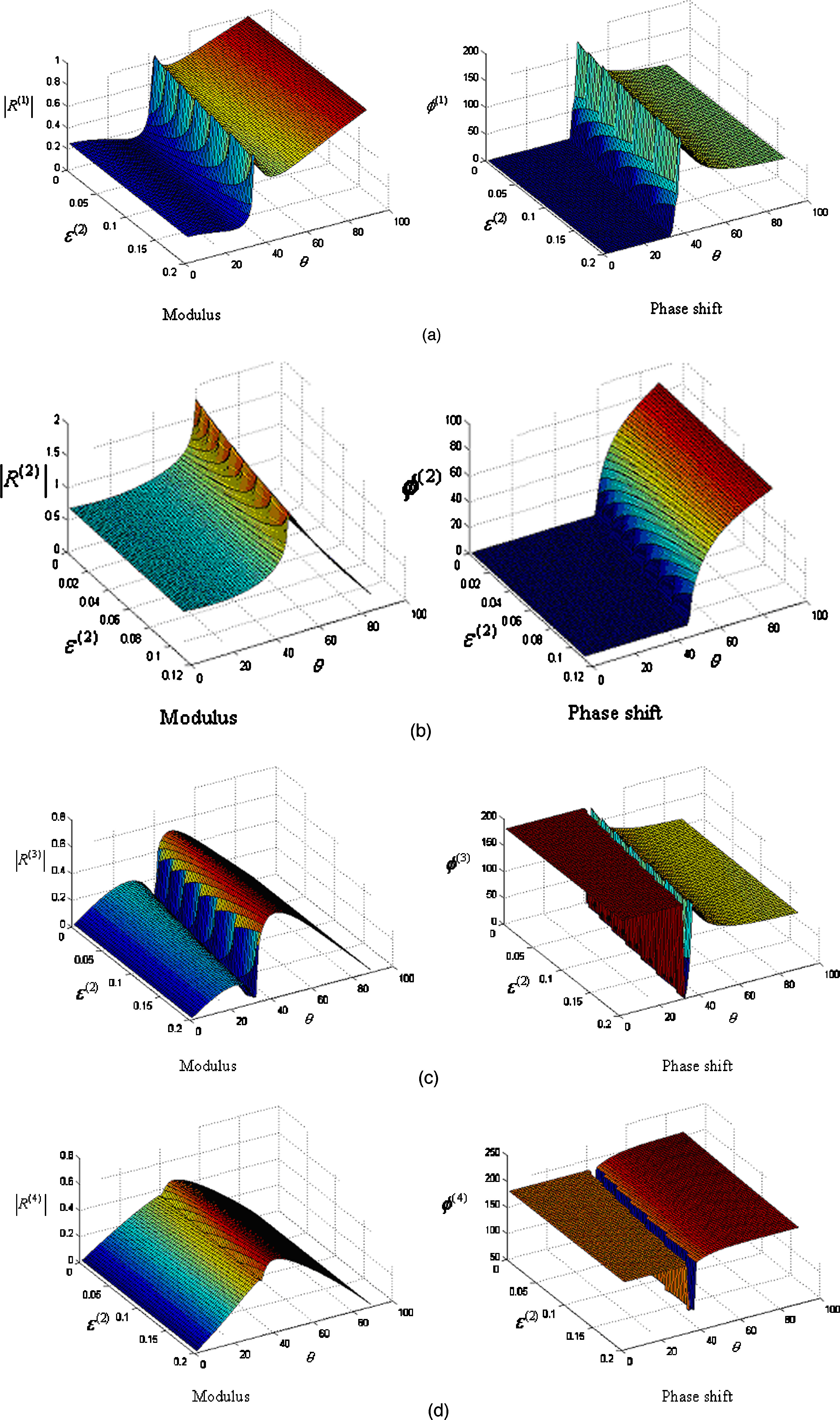
Figure 6. Reflection and refraction coefficients as functions of the incident angle and the anisotropic parameter for the interface between A-shale and O-shale: the left panel presents the amplitudes of the reflection and refraction coefficients and the right panel presents their corresponding phase angles [13][Ref. 13].
4.
Final Remarks
For the interface between two VTI media, it should be noted that the anomalous incident angle and the anomalous reflection are not universal for all interfaces of VTI media. The anomalous angle is most likely to occur only when there is strong anisotropy across the interface, e.g., at the interface of O-shale and A-shale, but not at the interface of O-shale and T-sandstone.
Intuitively, the anomalous incident angle and the anomalous reflection could also occur at the interface between two different sedimentary rock layers with strong anisotropy, e.g., at the interface either between VTI and TTI media or between TTI and TTI media. However, up to this moment, there is no published work to show this phenomenon at such an interface.
Finally, we consider the usefulness of these findings in the real world. While the existence and determination of anomalous reflections are theoretically substantial, their significance can be more fully realized if they are confirmed from experimental observations and applied to practical applications such as in geophysics and seismic exploration. Similar to many other cases of optical and acoustic phenomena [22][23][24][23-24], additional work needs to be done to fully understand their practical significance, which may further lead to productive industrial applications.
References
- L. Thomsen, “Weak anisotropy,” Geophys. 51(10), 1954-1966 (1986).
- J. Carcione, “Wave fields in real media: wave propagation in anisotropic, anelastic and porous media,” Elsevier, 2001.
- G. L. Backus, “Long-wave elastic anisotropy produced by horizontal layering,” J. Geophys. Res. 67, 4427–4440 (1962).
- V. Ĉervenŷ, “Seismic Ray Theory,” Cambridge University Press, 2001.
- I. Tsvankin, “P-wave signatures and notation for transversely isotropic media: an overview,” Geophys. 61, 467–483 (1996).
- K. Y. Kim, K. H. Wrolstad, F. Aminzadeh, “Effects of transverse isotropy on P-wave AVO for gas sands,” Geophys. 58, 883–888 (1993).
- A. Rüger, “P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry,” Geophys. 62, 713–722 (1997).
- N. C. Banik, “Velocity anisotropy of shales and depth estimation in the North Sea Basin,” Geophys. 52, 1654–1664 (1984).
- M. S. Sams, M. H. Worthington, M S. Khanshir, “A comparison of laboratory and field measurements of P-wave anisotropy,” Geophys. Prospect. 41, 189–206 (1993).
- L. Fa, L. Wang, L. Liu, Y. Zheng, Y. Zhao, N. Zhao, G. Li and M. Zhao, “Research progress in acoustical application to petroleum logging and seismic exploration,” The Open Acoustics Journal 6, 1-10 (2013), doi:1874-8376/13.
- L. Fa, M. Zhao, J. P. Castagna, Y. C. Liu, L. Wang, Y. Q. Wang and J. G. Sun, “On polarization of plane wave propagating inside elastic hexagonal system solids,” Science China: Physics, Mechanics & Astronomy 57, 1-12 (2014), doi: 10.1007/s11433-013-5363-3.
- Y. Zhao, N. Zhao, L. Fa and M. Zhao, “Seismic signal and data analysis of rock media with vertical anisotropy,” J. Modern Phys. 4, 11-18 (2013), doi:10.4236/jmp.2013.41003.
- L. Fa, R. Brown, J. Castagna, “Anomalous postcritical refraction behavior for certain transversely isotropic media,” J. Acoust. Soc. Am. 120, 3479-3492 (2006).
- L. Fa, M. Zhao, Liu, Y. C., Wang, L., Wang, Y. Q., and Sun, J. G. (2014). “Polarization of plane wave propagating inside elastic hexagonal system solids.” Sci. China-Phys. Mech. Astron. 57: 1-12.
- L. Fa and M. Zhao, “Recent progress in acoustical theory and applications,” in Understanding Plane Waves, Nova Science Publishers, Chapter 1, pp. 1-114, 2019.
- L. Fa and M. Zhao, “Recent development of an acoustic measurement system,” in Understanding Plane Waves, Nova Science Publishers, Chapter 2, pp. 115-147, 2019.
- L. Fa, J. Zhao, Y. Han and M. Zhao, “Polarization state of an inhomogeneously refracted compressional-wave induced at interface between two anisotropic-rocks,” J. of Acous. Soci. Ameri. 141, 1 (2017), doi:10.1121/1.4973410.
- L. Fa, J. Zhao, Y. Han, G. Li, P. Ding and M. Zhao, “The influence of rock anisotropy on the elliptical-polarization state of inhomogeneously refracted P-wave,” Science China Physics, Mechanics & Astronomy 59, 644301 (2016), doi:10.1007/S11433-015-00441-1.
- L. Fa, J. Castagna, H. Dong, “An accurately fast algorithm of calculating reflection/transmission coefficients.” Sci. China-Phys. Mech. Astron. 51, 823-846 (2008).
- L. Fa, Y. Fa, Y. Zhang, P. Ding, J. Gong, G. Li, L. Li, S. Tang and M. Zhao, “Anomalous incident-angle and elliptical-polarization rotation of an elastically refracted P-wave,” Scientific Reports 5, 12700 (2015), doi:10.1038/srep12700.
- L. Fa, J. P. Castagna, Z. Zeng, R. L. Brown and M. Zhao, “Effects of anisotropy on Time-Depth Relation in Transversely Isotropic Medium with a Vertical Axis of Symmetry,” Chin. Sci. Bulle. 55, 2241 (2010), doi: 10.1007/s11434-010-3186-4.
- L. Fa, J. Tang, Q. Zhang, M. Zhang, Y. Zhang, M. Liang, and M. Zhao, “Reflection and refraction of acoustic wave at VTI-TTI media interface,” Frontiers of Physics 15, 22601 (2020), doi: 10.1007/s11467-019-0934-z.
- Zhao and L. Fa, “The Goos-Hänchen Effect: An Intriguing Phenomenon from Optics to Acoustics,” Encyclopedia, 2019, v1, Available online: https://encyclopedia.pub/386.
- L. Fa and M. Zhao, “Network Modeling of Piezoelectric Transducers for Energy Conversion,” Encyclopedia, 2019, v1, Available online: https://encyclopedia.pub/367.
