Consider a biological evolutionary process.  We assume some (non-empty) finite set of offspring.  Assume each offspring is assigned as coming from a single set of parents in the previous generation.  There may be more than one offspring from each of set of parents.  This form of mathematical arrangement is called a surjection.   We have briefly described the mechanics of genetics; but we have also described much of mathematical anthropology.  

The finding that a process is a surjection does not just describe the algebra, it also predicts important results.  If we have found an inheritance process is a surjection, then each of the offspring is unique, but all of the acts of parental pairs must occur through identical (including isomorphic) means of reproduction; in fact here they require mathematical groups.  We demonstrate from published surveys that all offspring are unique.  Mathematical groups occur in both applications, determining the choices behind parental actions.  The surjection requirements are met in genetics in part because the mathematics are determined by the mathematical groups determined by quantum mechanics.  In culture theory, similar (and in some cases, isomorphic) groups occur.  Quantum mechanics is usually discussed for very small objects with incredibly short process intervals.  Here, the intervals of reproduction are observable within normal human perception, and for human cultural systems require decades of time for one generation system to be replaced by another. In genetics, counting of the number of offspring from each pair of “parents” is the actual number of offspring surviving from each pair to reproduce.  Each human culture has its own means of assigning offspring to parental pairs, which may include their surviving genetic offspring, but also may use culturally designated devices such as adoption. Since surjection also requires that distributions might be forecasted using the Stirling Number of the Second Kind that result allows culture theory to predict the numbers of offspring per assigned couple, and the percentage of adults engaging in that reproduction.  

1.  Foundation Discussion:  

In genetic inheritance and in human cultural systems each new offspring is assigned to be produced by a specific pair of the previous population.  In genetics, the biological descendants are the actual descendants of the identified parental pair.  In human systems, the descendants may be the actual biological descendants of the parental pair but may also cultural assignments, such as by (non-inherited) devices such as adoption.  In both cases, we have a mapping from each offspring to a particular set of parents.  The well know mathematical name for this relation is surjection.  Theorems on how inferences are made for surjections include ^[1] page 178, ^[2], ^[3] and ^[4] item 9 in his “Twelvefold Way” pages 69-79.  Due to these theorems, and more explicitly page 178 and ^[4] page 70.  Those theorems show that finding that a relation is a surjection also means that the newly created offspring individuals are each “unique”, and the entities to which offspring are assigned (their parental organisms) are “identical” in how they act. 

In genetic inheritance and in human cultural systems each new offspring is assigned to be produced by a specific pair of the previous population.  In genetics, the biological descendants are the actual descendants of the identified parental pair.  In human systems, the descendants may be the actual biological descendants of the parental pair but may also cultural assignments, such as by (non-inherited) devices such as adoption.  In both cases, we have a mapping from each offspring to a particular set of parents.  The well know mathematical name for this relation is surjection.  Theorems on how inferences are made for surjections include [1] page 178, [2], [3] and [4] item 9 in his “Twelvefold Way” pages 69-79.  Due to these theorems, and more explicitly [1] page 178 and [4] page 70.  Those theorems show that finding that a relation is a surjection also means that the newly created offspring individuals are each “unique”, and the entities to which offspring are assigned (their parental organisms) are “identical” in how they act. 

2.  Uniqueness of Individuals

When we say that the offspring of an evolutionary process are unique, we mean that there is at least one, but may be many differences between each of those offspring.  Radzevilavicius and Blackstone’s [5] very detailed review of the evolution of individuality of offspring populations shows that all individuals, of all species, created by evolution are also in some form unique; the reader should see that article for its many details.  [5] thus conclude “since [our review] … only relies on universal principles of life’s evolution, this framework can potentially be applied to all life, no matter what its chemistry, and wherever it is found” (page 1630).  It is also true that if we define a single species, there are common sets of DNA/RNA which define that single species,  But even within species identity by common DNA/RNA, there may also be recombination of the sequence of DNA/RNA codes [6]; [5] made a similar observation.  Thus despite isomorphism in the defining characteristics of a species (isomorphism of the DNA/RNA genetic codes that define that specific species), the uniqueness of individuals includes some genetic differences, which may be differences in the individuals own DNA/RNA pairs, and/or from recombination of DNA/RNA in their coding sequence.  

The mathematics that describes how biological evolution works began in the late 19th Century, representing the frequency or relative frequencies of alternative means of inheritance at specific alleles.  The first such description was Mendel [7], followed in the early 20

^th century by Bernstein ^[8]. Fischer ^[9]; Haldane ^{[10][11][12][13][14][15][16][17][18][19]}; Wright ^[20]; Nei ^[21]; Crow and Kimura ^[22] and others.  There are useful overall comparisons of those methods including ^{[23][24][25][26][27][28][29]} and others.  Though each of those authors uses somewhat different mathematical representations to determine the gene frequencies in specific cases, all show that devices such as those of Mendel allow many different forms of inheritance.  Because there are many possible allele sites in each organism, in nearly all organisms there may be diverse alleles at some sites; and hundreds, or thousands, or indeed many multiple thousands, of diverse allele sites per organism. Thus, while isomorphism of certain alleles at certain sites may define a specific species, the distinct frequencies in some or many other allele sites of individuals are one of the many reasons why many unique individual types of each species exist. 

century by Bernstein [8. 9]; Fischer [10]; Haldane [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]; Wright [21]; Nei [22]; Crow and Kimura [23] and others.  There are useful overall comparisons of those methods including [24, 25, 26, 27, 28, 29, 30] and others.  Though each of those authors uses somewhat different mathematical representations to determine the gene frequencies in specific cases, all show that devices such as those of Mendel allow many different forms of inheritance.  Because there are many possible allele sites in each organism, in nearly all organisms there may be diverse alleles at some sites; and hundreds, or thousands, or indeed many multiple thousands, of diverse allele sites per organism. Thus, while isomorphism of certain alleles at certain sites may define a specific species, the distinct frequencies in some or many other allele sites of individuals are one of the many reasons why many unique individual types of each species exist. 

3.  Identical Means for Genetic Reproduction by the Parental Generation

We must also show that each of the genetic parental pairs must use “identical” means of reproduction.  Petoukhov ^{[30][31][32][33][34]}; Petoukhov and Castro-Chaves ^[35];  Petoukhov and Hu ^[36]; Petoukhov, Petoukhova and Svirin ^[37]; Hainen ^[38]; Rakocevic ^[39]and others have demonstrated that the DNA/RNA devices used for genetic reproduction are described by mathematical groups.  In fact, the mathematical groups found for genetic reproduction are also the mathematical groups found for DNA by quantum mechanics.  The simplest basic description of genetic DNA/RNA is found in Figure 1 in ^[37], using descriptions of the 64 codons of DNA.  Figure 1 is based on the Figure 1 from ^[37] Figure 1 which shows all of the DNA alphabet of triplets with the arrangements of all members in accordance with the binary-oppositional signs of the bases A, C, G , T.

We must also show that each of the genetic parental pairs must use “identical” means of reproduction.  Petoukhov [31, 32,  33, 34, 35]; Petoukhov and Castro-Chaves [36];  Petoukhov and Hu [37]; Petoukhov, Petoukhova and Svirin [38]; Hainen [39]; Rakocevic [40] and others have demonstrated that the DNA/RNA devices used for genetic reproduction are described by mathematical groups.  In fact, the mathematical groups found for genetic reproduction are also the mathematical groups found for DNA by quantum mechanics.  The simplest basic description of genetic DNA/RNA is found in Figure 1 in [38], using descriptions of the 64 codons of DNA.  Figure 1 is based on the Figure 1 from [38] Figure 1 which shows all of the DNA alphabet of triplets with the arrangements of all members in accordance with the binary-oppositional signs of the bases A, C, G , T.

Figure 1:  64 CODONS OF DNA

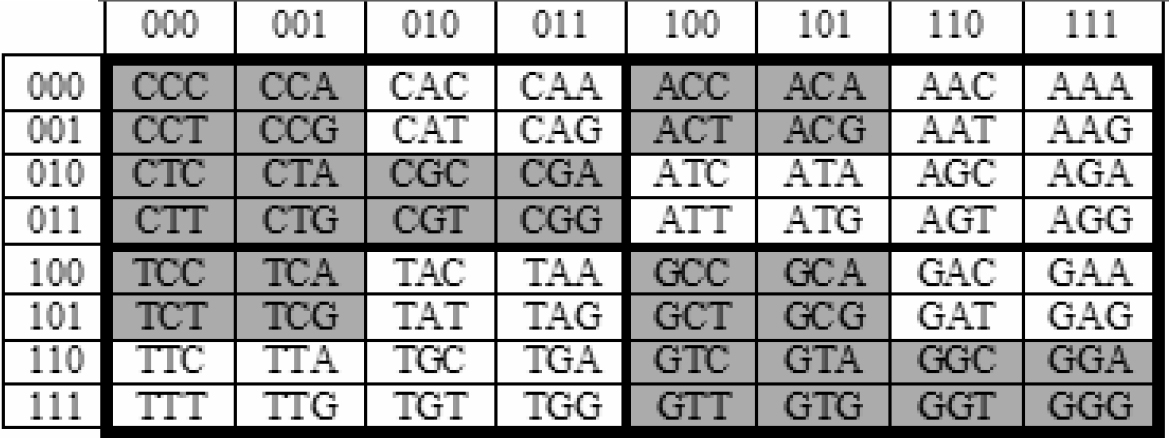
4.  Kinship

The realization that surjection affects cultural studies also requires understanding that basic cultural descriptions are also mathematical groups.  Ballonoff ^[40][41][42] recently reviewed the literature of mathematical anthropological description, in relation to the ability of a system to survive.  The earliest paper ^[43] for mathematical description of kinship is from 1882. ^[43] modeled strings of symbols to represent semantic concepts, such as “MBD” (mothers brothers daughter) for an instance of part of the English term “first cousin”.   In 1945 ethnographer Ruheman ^[44] created the first description of kinship which identified objects that are clearly mathematical groups,.  She denoted each cultural system by placing names of kinship relations onto finite sets of offspring, used diagrams to show how a terminology relates those sets of labels onto representative sets of parents, and assumed each system had distinct generations. ^[44] page 543 said: “… The system must be self-contained and consistent; must provide a sufficient number of descent lines (a) to enable every member to select a spouse from his own generation; (b) to allow space for every distinct relationship term; and no term may appear more than twice … in any one generation.   “… The system must be able to reproduce itself after a number of generations. …”.  She also said ^[44] page 576 that by using mathematical representations: “… It is independent of any special principles, which might at best be controversial, and proceeds simply from a systematic arrangement of the recorded facts; … It enables the dominating features of even a very complex system of kinship terms to be brought into full view in a single picture; … It makes possible the comparison and classification of widely divergent kinship systems, and provides a useful check on the completeness of our information.”  Ruheman’s methods do not therefore discuss many of the issues often treated in non-mathematical analysis of cultural systems. Avoiding non-mathematical descriptions is one of her purposes. 

The realization that surjection affects cultural studies also requires understanding that basic cultural descriptions are also mathematical groups.  Ballonoff [41, 42] recently reviewed the literature of mathematical anthropological description, in relation to the ability of a system to survive.  The earliest paper [43] for mathematical description of kinship is from 1882.  [43] modeled strings of symbols to represent semantic concepts, such as “MBD” (mothers brothers daughter) for an instance of part of the English term “first cousin”.   In 1945 ethnographer Ruheman [44] created the first description of kinship which identified objects that are clearly mathematical groups,.  She denoted each cultural system by placing names of kinship relations onto finite sets of offspring, used diagrams to show how a terminology relates those sets of labels onto representative sets of parents, and assumed each system had distinct generations.  [44] page 543 said: “… The system must be self-contained and consistent; must provide a sufficient number of descent lines (a) to enable every member to select a spouse from his own generation; (b) to allow space for every distinct relationship term; and no term may appear more than twice … in any one generation.   “… The system must be able to reproduce itself after a number of generations. …”.  She also said [44] page 576 that by using mathematical representations: “… It is independent of any special principles, which might at best be controversial, and proceeds simply from a systematic arrangement of the recorded facts; … It enables the dominating features of even a very complex system of kinship terms to be brought into full view in a single picture; … It makes possible the comparison and classification of widely divergent kinship systems, and provides a useful check on the completeness of our information.”  Ruheman’s methods do not therefore discuss many of the issues often treated in non-mathematical analysis of cultural systems. Avoiding non-mathematical descriptions is one of her purposes. 

Ruheman’s illustrations use “=“ for a "marriage" between two individuals; two sets of parallel but opposite arrows between individuals as “brothers and/or sisters”; and placed objects into columns labelled m and f for males and females.  In an illustration [44] page 547, Ruheman labeled A and B for moiety names: 

Figure 2:  Example from Ruheman’s study of Australian kinship

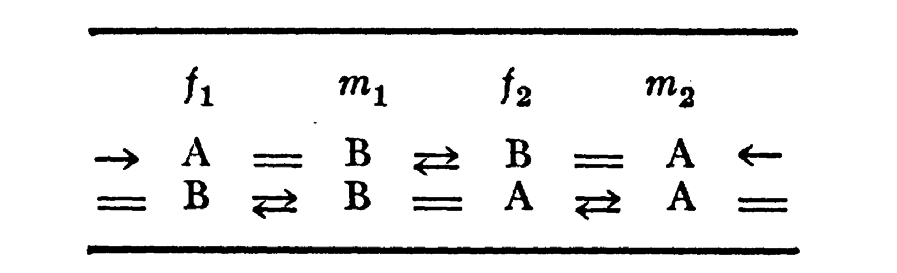
Descents of a male of A are also called A; descendants of a male of B are also called B; the top layer is one generation of two sets of moieties, with two marriages, which reproduces in one generation another set of A and B moieties.  The arrows or = signs on each end of each line connect to the persons on the other end of each line.  This system thus has two sets of marriages in each generation; each A always marries a B; and it has what we later call a “structural number” s = 2, as the minimal group found here has group order 2 among the two marriages per generation it depicts.  The mathematical groups for each minimal set of kinship terms described by Ruheman is also now called the “minimal structure” [41] of that system of kinship description; and it is also described [41] as the “history” of that system since they describe how possible parental pairs of that culture may be created.  The minimal structure is not a literal description of how all marriages work, though in some cases some empirical relations can also look like the Ruheman minimal descriptions in some ethnographies.

Ruheman uses rules of that culture’s language to derive the basic minimal groups.  Related to this result, Petoukhov [45] demonstrated that there are similar mathematics behind literary texts (thus including kinship in human languages) and long genetic texts; and when analyzing human Dravidian kinship categories, Vaz [46] showed that mathematical representation of DNA/RNA (such as using codes in Figure 1) was isomorphic to the groups that minimally represent the Dravidian kinship categories. 

While Ruheman created the notion, the most referenced “first” version using group mathematics for kinship was Andre Weil ^[45], in an appendix to Claude Levi-Strauss’ 1947

While Ruheman created the notion, the most referenced “first” version using group mathematics for kinship was Andre Weil [47], in an appendix to Claude Levi-Strauss’ 1947

The elementary structures of kinship ^[47][48]. Weil was then expanded by ^{[49][50][51][52]}.   Use of Cayley groups was described in ^[53]. While groups require an associative operation, the first work showing that kinship rules are actually non-associative algebras was ^[54]. But a non-associative algebra, which includes most languages for example, can have an associative sub-set (the kinship rules for example), which are allowed by ^[54] and required by . ^[55] derives mathematical kinship groups entirely from purely mathematical assumptions. ^[56][57] elaborated many group-theoretical examples. ^[58] reviewed Weil’s original work and its subsequent history. ^[59] extended Weil’s work by using semigroups and homomorphisms among semigroups, as well as groups.  Other extensions include ^{60][61][62][63][64][65][66][67][68][69][70][71][72][73]};  many of those  also related kinship math  to other concepts of cultural order; sought the same results.   Thus Read ^[67] page 54 cited the necessity of mathematical groups in kinship descriptions:  “… Because the core structure for classificatory terminologies has inverses and not just reciprocity between ascending and descending kin terms, the core structure is a group; that is, an algebra with an (associative) binary product, an identity element, and an inverse for each element in the algebra.”  Read is thus also describing the empirical facts that make Ruheman’s concepts necessary. 

[48]. Weil was then expanded by [49, 50, 51, 52].   Use of Cayley groups was described in [53]. While groups require an associative operation, the first work showing that kinship rules are actually non-associative algebras was [54].  But a non-associative algebra, which includes most languages for example, can have an associative sub-set (the kinship rules for example), which are allowed by [54] and required by [42].  [55] derives mathematical kinship groups entirely from purely mathematical assumptions.  [56, 57] elaborated many group-theoretical examples.  [58] reviewed Weil’s original work and its subsequent history.  [59] extended Weil’s work by using semigroups and homomorphisms among semigroups, as well as groups.  Other extensions include [60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73];  many of those  also related kinship math  to other concepts of cultural order; [54] sought the same results.   Thus Read [67] page 54 cited the necessity of mathematical groups in kinship descriptions:  “… Because the core structure for classificatory terminologies has inverses and not just reciprocity between ascending and descending kin terms, the core structure is a group; that is, an algebra with an (associative) binary product, an identity element, and an inverse for each element in the algebra.”  Read is thus also describing the empirical facts that make Ruheman’s concepts necessary. 

5.  Culture and Population Measurements

In genetics, the ability to predict future generations depends on how the genes cause surviving individuals;  the relevant population number to measure that per parental couple is their actual reproduction.  In human cultures, the fact that the relation is a surjection also predicts changes in the demography of any society following one or a mixture of specific histories.    But for “reproduction” assigned to each assigned  human parental pair, there may be actual genetics between them, but there may also be “cheating” (sometimes known but often not known to other members of the population), assignment of other non-genetic offspring by adoption, and maybe other means of assigning offspring to the each parental pair.   But ^[1][2][3][4] show that surjection also requires that counting the of the possible numbers of offspring to parental pairs can be estimated using the Stirling Number of the Second Kind (SNSK).  We briefly discuss how to do that in Equations 1 through 4 below (assuming predictions that seek equilibrium size), given the histories of that system.  Ethnographic studies are from several months to several years; but observations over several decades are needed to fully verify the human populations predictions offered here. However the results described by the references given here or in their citations imply the predictions are correct.

In genetics, the ability to predict future generations depends on how the genes cause surviving individuals;  the relevant population number to measure that per parental couple is their actual reproduction.  In human cultures, the fact that the relation is a surjection also predicts changes in the demography of any society following one or a mixture of specific histories.    But for “reproduction” assigned to each assigned  human parental pair, there may be actual genetics between them, but there may also be “cheating” (sometimes known but often not known to other members of the population), assignment of other non-genetic offspring by adoption, and maybe other means of assigning offspring to the each parental pair.   But [1, 2, 3, 4] show that surjection also requires that counting the of the possible numbers of offspring to parental pairs can be estimated using the Stirling Number of the Second Kind (SNSK).  We briefly discuss how to do that in Equations 1 through 4 below (assuming predictions that seek equilibrium size), given the histories of that system.  Ethnographic studies are from several months to several years; but observations over several decades are needed to fully verify the human populations predictions offered here. However the results described by the references given here or in their citations imply the predictions are correct.

Many things affect population size; we do not here attempt to identify most of those.  The formulas that determine the objects described by D in the illustration just below are results from demographic processes.  The Leslie matrix ^[74][75] produces a growth rate and stable age distribution as eigenvalues and eigenvectors of a matrix of age-structured mortality and fertility or fecundity rates.  This reflects Lotka ^[76] who assumes the “normal” demographic discussion of populations growth is analogous to “capital” growth in economics.  Neither the Leslie matrix nor the Lotka models treats the cultural system, and thus do not treat consequences on population change due to changes in the cultural system.   But the surjection requirement of using SNSK statistics allows us to predict how the demographics of a society may change, as the histories change.  To explore this ^[77] defined: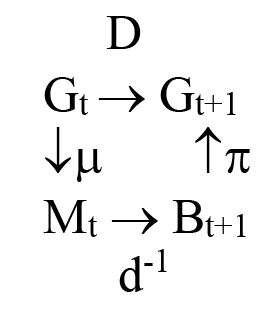    

Many things affect population size; we do not here attempt to identify most of those.  The formulas that determine the objects described by D in the illustration just below are results from demographic processes.  The Leslie matrix [74, 75] produces a growth rate and stable age distribution as eigenvalues and eigenvectors of a matrix of age-structured mortality and fertility or fecundity rates.  This reflects Lotka [76] who assumes the “normal” demographic discussion of populations growth is analogous to “capital” growth in economics.  Neither the Leslie matrix nor the Lotka models treats the cultural system, and thus do not treat consequences on population change due to changes in the cultural system.   But the surjection requirement of using SNSK statistics allows us to predict how the demographics of a society may change, as the histories change.  To explore this [77] defined: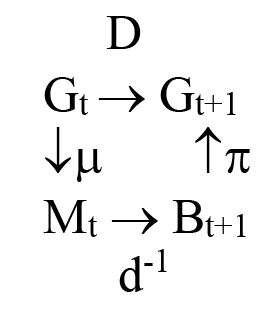    

D         summarizes biological population operators for genetics and demographics of the population at the indexed time t,

M

_t

       the sets of married couples at time t, with M

_t

⊆ G

_t

B

_t+1

      a partition of G

_t+1

into sets of persons with the same parents, with B

_t+1

⊆ G

_t+1

μ          a surjection corresponding to assignments of M

_t

,

π          a partition of G

_t+1

showing kin groups of a population within a generation t+1, as assigned by the cultural rules of marriage

d

^-1

       a surjection corresponding to descent

d          an injection corresponding to ancestor

so that the d

^-1

surjection maps the progress of population change following sets of descendants in generation t + 1 onto the sets of their parents in generation t. 

Let s be the structural number of history a.  Let n

_s

  = 

average family siz

e of a system with structural number s.  Define the proportion of (socially ascribed)

reproducing females

as p

_s

.  Let p

_s

= 2/n

_s

.  The specific values of p

_s

, and n

_s

by structural number s as fixed numbers, given s are described in [3] appendix 2, [42], and [78, 79].  Note that n

_s

is always ≥ 2, so n*p = 2, or 

1.     ½ (n

_s

* p

_s

) = 1.

Since the exponential form e

^r(t)

 = 1 then we can also derive a general “equity growth” equation for any system with structural number s:

2.    e

^r(t)

 =  ½ n*p.

Thus equity growth r(t) is distinct from capital growth idea per Lotka, which we here call R(t).  We thus next derive an estimate of capital growth R(t) from the equity growth r(t).

When we use specifically the values n

_s

, p

_s

given a history of structural number s (see also [42, 79]) then n

_s

p

_s

= 2'  Then Equation 2 shows r(t) = 0, so if we have only one structural number per generation,  the predicted n

_s

and p

_s

allow that history to have neither growth nor decline.  As structural number s increases (above s = 3), then [3, 42, 78, 79] show that values of n

_s

increase and p

_s

decrease, to maintain cultural stability with  r(t) = 0.  As the cultural systems gets “more complex” (as the structural number s increases) then n

_s

per household also increases; this is similar to the notion that as general systems become more complex, their size must increase to maintain the same level of reliability – which here is when r(t) = 0.

Now assume the population at time t use some set of histories α, … β.  Then the for each α the proportion of each G

_t

using history α is v

_αt

, the proportion of G

_t

using history β is v

_βt

, etc.  We require that 0 ≤ v

_αt

,, …, v

_βt

 ≤ 1 and ∑v

_αt

= 1 over all histories allowed in time period t.  Then the average n(t) = ∑v

_αt

n

_s

over all histories allowed at time t; the average p(t) = ∑v

_αt

p

_s

over all histories allowed at time t; and we get an equation that allows prediction at time t of the time-dependent average population measures for n(t), p(t) and r(t) as the percentages of histories α, … β change:  

3.     e

^r(t)

  =  ½ n(t)*p(t).

From  whenever all rules have the same structural number (or all have only s = 2 or 3) and r(t) = 0 .  But r(t) ≠ 0 whenever there is a change in cultural dynamics by allowing rules with more than one structural number (and at least one of structural number > 3); that is, all such changes cause population growth (or decline). This result empirically is well known by anthropologists: as cultures change, population statistics can also change.  It is however predicted by recognizing surjection.   To then relate r(t) to the demographic R(t) we now apply the mathematics developed for analysis of financial leverage (see ^[80] Chapters 3 and 4, ^[78] especially its Equation 17, and ^[79]), and thus:

From [42, 79] whenever all rules have the same structural number (or all have only s = 2 or 3) and r(t) = 0 .  But r(t) ≠ 0 whenever there is a change in cultural dynamics by allowing rules with more than one structural number (and at least one of structural number > 3); that is, all such changes cause population growth (or decline). This result empirically is well known by anthropologists: as cultures change, population statistics can also change.  It is however predicted by recognizing surjection.   To then relate r(t) to the demographic R(t) we now apply the mathematics developed for analysis of financial leverage (see [80] Chapters 3 and 4, [78] especially its Equation 17, and [79]), and thus:

4.    R(t)  =  2 p(t)r(t) / [p(t)2 + 2r(t)]. 

See ^[79] for more citations of examples. 

See [41, 42, 78, 79] for more citations of examples. 

6.  The Use of Quantum Logic

In genetics, the recognition that we have a surjection requires us to apply quantum theory to the molecules of inheritance - and thus significantly, to use quantum mechanics to infer biological evolution; see citations in Part 3 above.  The notion that quantum mechanics would create biological evolution was first shown by citations to genetic selection, to the knowledge of this author, by Schroeck [81], pages 223 - 253.  Schroeck showed that in the mammals called bats, identification of other objects in flight was described by quantum mechanical devices inside the bat, when the speeds of object became fast enough.  The more extensive work by Petoukhov and others (Part 3 citations) used notions of quantum mechanics similar to those found by Schroeck. 

Mathematical anthropology is certainly not a “quantum” theory.  But the ideas of quantum logic use both full and partial algebras, thus specific parts of quantum logic are also useful in describing cultural theory; for example ^{[82][83][84][85]} use quantum logic in large part because the underlying math objects might not be full.  There are empirically probably less than 20 distinct forms of kinship systems (though there may be thousands of cultures with distinct languages in which they are expressed), and most of those systems have structural numbers at or well under s = 16.  If we look at combinations of cultures and seek to create a lattice of all structural numbers in the lattice, the product of all structural numbers can create a lattice whose top-group order may be well above 16.  Empirically there may be no such systems.  Another way to state this is that there may be sets of possible histories, not all of which can be allowed to find each other from within that set.  That in turn may also create possible changes among histories in which some ranges of values of n(t) and of p(t) - hence of r(t) and R(t) - are also not allowed.  The homotopy of these systems may therefore tell us a lot on which kinds of cultural systems might evolve into each other or in which sequences, and which if any might not evolve; see also.  The possible limits to which sequences of histories might be allowed or inhibited to co-exist or transition to each other needs further work, both mathematically and empirically.

Mathematical anthropology is certainly not a “quantum” theory.  But the ideas of quantum logic use both full and partial algebras, thus specific parts of quantum logic are also useful in describing cultural theory; for example [42, 82, 83, 84, 85] use quantum logic in large part because the underlying math objects might not be full.  There are empirically probably less than 20 distinct forms of kinship systems (though there may be thousands of cultures with distinct languages in which they are expressed), and most of those systems have structural numbers at or well under s = 16.  If we look at combinations of cultures and seek to create a lattice of all structural numbers in the lattice, the product of all structural numbers can create a lattice whose top-group order may be well above 16.  Empirically there may be no such systems.  Another way to state this is that there may be sets of possible histories, not all of which can be allowed to find each other from within that set.  That in turn may also create possible changes among histories in which some ranges of values of n(t) and of p(t) - hence of r(t) and R(t) - are also not allowed.  The homotopy of these systems may therefore tell us a lot on which kinds of cultural systems might evolve into each other or in which sequences, and which if any might not evolve; see also [42].  The possible limits to which sequences of histories might be allowed or inhibited to co-exist or transition to each other needs further work, both mathematically and empirically.

Many ethnographies discuss a cultural system as if there is only one history present in that population. Therefore their discussion does not talk of “probabilities” that a culture is in some specific history; they assume a specific history, and thus no probabilities are needed.  Applications of the same history at each instance of time also means that there is no change in demographics of the population: if the same structural number repeats, then the predictions of n(t) and p(t) do not change; they remain at n

_s

and p

_s.   demonstrated that either cultural histories of a society follow one history, consistently, or may have more than one history possibly present at each instance of t.  But when probabilities are needed they use Pauli coefficients, as complex probabilities simplify following specific paths.  Thus while not an analogy to quantum theory, complex Hilbert space probabilities can also be used for cultural theory.    

.   [41] demonstrated that either cultural histories of a society follow one history, consistently, or may have more than one history possibly present at each instance of t.  But when probabilities are needed [42] they use Pauli coefficients, as complex probabilities simplify following specific paths.  Thus while not an analogy to quantum theory, complex Hilbert space probabilities can also be used for cultural theory.    

Quantum mechanics ^[86][87][88] can use a “consistent histories” approach, in which the same history is consistently followed in each generation of a descent structure. This approach defines a

Quantum mechanics [86, 87, 88, 89] can use a “consistent histories” approach, in which the same history is consistently followed in each generation of a descent structure. This approach defines a

descent map

(called “descent” in quantum theory as well), which, like the descent map of genetics or in cultural theory, is a partial order.  In physics, the physical object in each instance of t+1 is a copy of the same object as in time t; only its momentum or location may have changed. In both genetics and culture theory the objects at time t+1 are descendants of the objects at time t; they are

distinct objects, not the same objects as assumed in physical theory.  The single objects discussed in physics as non-commutative have been found in physics to have “uncertainty”.  Our Part 5 here (see also^[42] ) found that when objects in culture theory are similarly non-commutative our equations forecast r(t) ≠ 0 and thus also that generation growth (or decline) occurs; we get significant changes, but we do not get uncertainty.  Nor does uncertainly apparently occur in the genetic applications (our Part 3).  We thus also hope that mathematicians, perhaps with philosophical guidance, and provide further ideas on these differences. 

objects, not the same objects as assumed in physical theory.  The single objects discussed in physics as non-commutative have been found in physics to have “uncertainty”.  Our Part 5 here (see also [42]) found that when objects in culture theory are similarly non-commutative our equations forecast r(t) ≠ 0 and thus also that generation growth (or decline) occurs; we get significant changes, but we do not get uncertainty.  Nor does uncertainly apparently occur in the genetic applications (our Part 3).  We thus also hope that mathematicians, perhaps with philosophical guidance, and provide further ideas on these differences.