Neuroimaging is a widely available, less-invasive method to investigate the whole brain of humans, and with neuroimaging, the brain’s morphological and microstructural features can be obtained. A neuroimaging-based brain-age estimation can provide a reliable neuropsychiatric biomarker at the single-subject level. In addition, brain MRI—particularly T1-weighted structural Magnetic resonance imaging (MRI)—is a widely available examination in most countries, which may support easier and wider clinical applications of brain-age analyses. Considering the utility, availability, and reproducibility of neuroimaging-based brain-age estimations for single patients, brain age can be expected to become a useful personalized biomarker in neuropsychiatry.
1. Aging, Disease, and the Brain
The aging process in humans is associated with the progressive decline of various physiological and organ functions
[1], and many diseases including cancer, cardiovascular disease, diabetes, and dementia are associated with aging
[2]. It is not uncommon for elderly people to suffer from multiple diseases simultaneously. Since humans’ bodies change with age and as humans are living longer in several regions of the world, the aging process has become a key issue in public health, disease prevention, and treatment. Many discussions concerning the pathological meaning of aging in the context of epigenetic change, proteotoxic or oxidative stress, and telomere damage have thus been conducted
[3].
The brain is also affected by aging
[4]. In the early stage of life, the aging process is regarded as brain development in which the brain matures, and children usually experience an increase in their cognitive ability along with their physical growth. During late adulthood, the brain aging process has different effects, e.g., a decline of cognitive function, and advancing age is associated with neurodegeneration, particularly Alzheimer’s disease and other forms of dementia
[5][6][5,6]. If the aging process of the brain could be measured precisely and accurately, the findings may have potential as biomarkers for neuropsychiatric disorders. In fact, frameworks to quantify the age of a human brain have been attempted for several decades
[7]. Today, advances in medical imaging and analytical methods (especially machine learning) have allowed the calculation of an individual’s biological age from the extracted biological features
[8]. The frameworks that are now used to estimate the age of an individual’s brain have the potential to provide useful, objective, and personalized biomarkers for neurological and psychiatric disorder
2. Neuroimaging-Based Brain Age Estimation
2.1. Theory of Neuroimaging-Based Brain-Age Estimation
In 2010, Katja Franke and her peers developed a prediction model that was able to estimate a subject’s age based on brain imaging data and the use of a regression machine-learning model
[9]. The output of a brain-age estimation framework has been called the “brain age-delta,” “brain predicted age difference (Brain-PAD),” “brain age gap estimation (BrainAGE),” and “brain age gap (BAG),” each of which is computed by deducting the estimated brain age from the subject’s chronological age.
HIn this re
re, itview, we refer
s to “brain age-delta” as the output of a brain-age estimation framework. The brain age-delta is known as a heritable biomarker for both monitoring cognitively healthy aging and identifying age-associated disorders
[8]. There are three possibilities for a brain age-delta value: (i) a brain age-delta close to zero, representing normal brain aging, (ii) a positive brain age-delta (i.e., estimated brain age > chronological age), representing an older-appearing brain, and (iii) a negative brain age-delta (i.e., estimated brain age < chronological age), representing a younger-appearing brain.
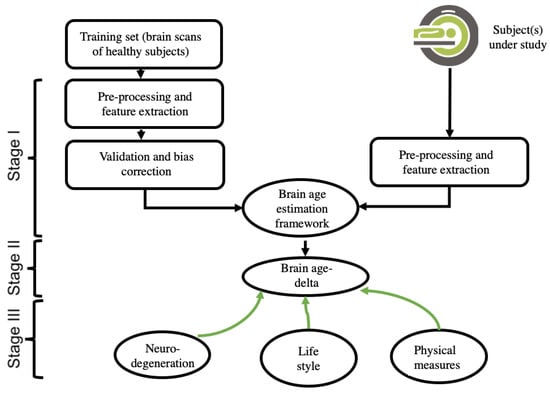
A brain-age estimation study is generally composed of three main stages: (i) creating a prediction model by using extracted brain features and a regression machine-learning model, validation, and bias correction; (ii) computing the brain age and brain age-delta for the subject under study; and (iii) interpreting the results, including the use of a within-group and/or a between-groups analysis. Figure 1 depicts the pipeline of a typical brain-age estimation study.
Figure 1.
This is a figure. Schemes follow the same formatting.
2.2. Input Data and Feature-Extraction Methodologies of Neuroimaging
One of the key concerns among researchers attempting to develop a brain-age estimation framework is the selection of the input data. Each modality offers unique insights into the brain. For example, fluorodeoxyglucose-positron emission tomography (FDG-PET) scans provide information about the brain’s glucose metabolism, whereas magnetic resonance imaging (MRI) data provide information about the anatomy of the brain. Among the different brain, MRI modalities such as T1-weighted MRI images (T1w MRI), T2-weighted MRI images (T2w MRI), resting-state functional (f)MRI, and fluid-attenuated inversion recovery (FLAIR), the majority of brain-age estimation studies have used T1w MRI data. The main reason for using T1w MRI is because it is more readily available than other modalities
[10][15]. Brain age frameworks generally require a large dataset for training a prediction model, and many public neuroimaging datasets such as ADNI (
https://www.adni.loni.usc.edu, accessed on 31 October 2022), PPMI (
https://www.ppmi-info.org, accessed on 31 October 2022), IXI (
http://brain-development.org/ixi-dataset/, accessed on 31 October 2022), and OASIS (
https://www.oasis-brains.org/, accessed on 31 October 2022) have provided a great number of T1W MRI scans for research studies.
Each brain imaging modality requires a specific feature extraction strategy. The feature extraction approaches for T1w MRI data can be classified into two categories: (i) voxel-wise methods (e.g., statistical parametric mapping [SPM],
http://www.fil.ion.ucl.ac.uk/spm, accessed on 31 October 2022)
[8][11][12][8,16,17], which use gray matter (GM) and/or white matter (WM) signal intensities as brain features; and (ii) region-wise methods (e.g., FreeSurfer,
http://surfer.nmr.mgh.harvard.edu/, accessed on 31 October 2022)
[13][18], which use the subcortical and cortical and measurements of volume, surface, and thickness values as brain features. Both voxel-wise and region-wise feature extraction approaches have been widely used in T1-w MRI-driven brain-age estimation studies
[14][15][16][19,20,21].
A direct comparison of voxel-wise and region-wise metrics as well as their integration in the accuracy of brain age has been conducted
[17][12]. For functional MRI-driven brain-age frameworks, the extracted features can be functional connectivity (FC) measures between brain regions or intrinsic connectivity networks and voxel-wise whole-brain FC measures (e.g., FSLNets,
https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FSLNets, accessed on 31 October 2022)
[18][19][22,23]. In terms of the PET modality, the extracted features for estimating brain ages include measurements of brain metabolism (i.e., PET regional total glucose, aerobic glycolysis, oxygen) and cerebral blood flow
[18][19][22,23]. White-matter microstructure measurements such as mean diffusivity, fractional anisotropy, axial diffusivity, and radial diffusivity have been employed as brain features for a diffusion tensor imaging (DTI)-based brain age framework
[20][24].
2.3. Data Reduction, Validation, and Bias Adjustment Neuroimaging Methodologies
The ‘curse of dimensionality’ is one of the major concerns in developing a brain-age estimation framework, particularly when the number of brain features is far higher than the number of samples (e.g., in voxel-based feature extraction strategies). High-dimensional data can give rise to some substantial issues in a prediction model, such as overfitting and decreased computational efficiency. A data reduction technique that can decrease the high dimensionality of data and diminish redundant information is thus required. In the area of brain-age estimation, most studies have used the principal component analysis (PCA) strategy, which is an unsupervised learning technique
[9][14][9,19]. The effect of the number of principal components on the accuracy of brain-age predictions has been investigated
[9]. The number of principal components may influence the prediction accuracy in a brain age estimation framework. However, it can be adjusted to achieve maximum accuracy in the training set
[9].
After a prediction model is developed, it is critical to validate the model’s prediction accuracy. Most studies in the field of brain-age estimation have used a K-fold cross-validation strategy (e.g., K = 5 or 10) to assess the prediction performance on a training set
[11][16][17][21][12,14,16,21]. In the K-fold cross-validation technique, the data are randomly divided into K folds, and the learning process is repeated K times so that K-1 folds are used for training a prediction model, and the remaining fold is used as a test for each iteration. To assess the prediction accuracy, researchers generally use the coefficient of determination (R2) between the subjects’ chronological age and estimated age, the MAE, and root mean square error (RMSE) metrics.
Many brain-age estimation studies have reported age dependency on the prediction outputs, and this is considered a substantial issue in brain-age frameworks
[16][22][13,21]. This bias, which could be a result of regression dilution bias, may adversely affect the predicted values and alter the interpretation of results. Several techniques have been proposed to diminish this bias (i.e., age dependency)
[16][22][23][13,21,25]. For instance, Le and colleagues proposed using chronological age as a covariate in the statistical analyses and interpreting the results
[24][26]. However, it should be highlighted that Le’s method is appropriate for group comparison only and not able to deliver bias-free brain age values at the individual level. A bias adjustment strategy is proposed in
[16][21] (i.e., Cole’s method) that uses the intercept and slope of a linear regression model of estimated brain age against chronological derived from the training set. The bias-free Brain-age values in the test sets are then calculated by subtracting the intercept from the predicted brain age and dividing by the slope
[16][21]. The most recent bias adjustment technique is suggested in
[22][13] (i.e., Beheshti’s method) which computes offset values for test subjects on the basis of the intercept and slope of a linear regression model of brain age-delta against chronological age achieved from the training set. Then, the bias-free Brain-age values are computed by subtracting the offset values from the estimated brain-age values
[22][13]. A direct comparison of these bias adjustment techniques has shown that Beheshti’s method greatly reduces the variance of the predicted ages, whereas Cole’s method increases it
[22][13].
2.4. Machine-Learning Methodologies
One of the important steps in developing a brain-age estimation framework is choosing a regression machine-learning model. A regression model establishes a pattern between independent variables (here, brain features) and the corresponding dependent variable (a subject’s chronological age) based on the training dataset, and the model uses this pattern to predict the brain age based on unseen data (i.e., independent test datasets). The most widely used traditional regression algorithms include support vector regression (SVR)
[14][19][19,23], relevance vector regression (RVR)
[9], Gaussian process regression
[16][21], an ensemble of gradient-boosted regression trees
[23][25], and XGBoost
[23][25]. It has been demonstrated that the type of regression algorithm used influences the prediction accuracy and the interpretation of outcomes in brain-age frameworks
[21][14].
In addition to the traditional regression algorithms, deep learning models have become a prominent methodology in the area of brain-age estimation
[25][11], as they can be used to develop more accurate prediction models. A major advantage of deep learning models is that they can be applied directly with 3D brain image data and incorporate feature extraction, data reduction, and prediction stages into a unified system. The main challenge of deep learning-based brain-age estimation frameworks is that this methodology requires a large dataset to train a model. In 2017, James Cole and his peers developed the first deep learning-based brain-age estimation framework, with a 3D convolutional neural network (CNN) that uses 3D gray matter and 3D white matter intensity maps as the input data
[25][11]. Other deep learning architectures used in brain-age estimation frameworks include feed-forward neural networks, VGGNet
[26][27], ResNet
[27][28], U-Net
[28][29], and an ensemble of CNN architectures
[29][30].