1. Constructions

There are many different ways of constructing the Sierpinski triangle.

1.1. Removing Triangles

The Sierpinski triangle may be constructed from an equilateral triangle by repeated removal of triangular subsets:

1. Start with an equilateral triangle.
2. Subdivide it into four smaller congruent equilateral triangles and remove the central triangle.
3. Repeat step 2 with each of the remaining smaller triangles forever.

Each removed triangle (a trema) is topologically an open set.^[1] This process of recursively removing triangles is an example of a finite subdivision rule.

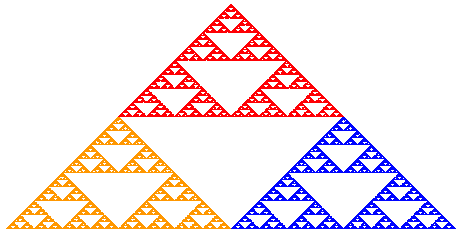
1.2. Shrinking and Duplication

The same sequence of shapes, converging to the Sierpinski triangle, can alternatively be generated by the following steps:

1. Start with any triangle in a plane (any closed, bounded region in the plane will actually work). The canonical Sierpinski triangle uses an equilateral triangle with a base parallel to the horizontal axis (first image).
2. Shrink the triangle to 1/2 height and 1/2 width, make three copies, and position the three shrunken triangles so that each triangle touches the two other triangles at a corner (image 2). Note the emergence of the central hole—because the three shrunken triangles can between them cover only 3/4 of the area of the original. (Holes are an important feature of Sierpinski's triangle.)
3. Repeat step 2 with each of the smaller triangles (image 3 and so on).

Note that this infinite process is not dependent upon the starting shape being a triangle—it is just clearer that way. The first few steps starting, for example, from a square also tend towards a Sierpinski triangle. Michael Barnsley used an image of a fish to illustrate this in his paper "V-variable fractals and superfractals."^[2]

The actual fractal is what would be obtained after an infinite number of iterations. More formally, one describes it in terms of functions on closed sets of points. If we let d_A denote the dilation by a factor of 1/2 about a point A, then the Sierpinski triangle with corners A, B, and C is the fixed set of the transformation d_A ∪ d_B ∪ d_C.

This is an attractive fixed set, so that when the operation is applied to any other set repeatedly, the images converge on the Sierpinski triangle. This is what is happening with the triangle above, but any other set would suffice.

1.3. Chaos Game

If one takes a point and applies each of the transformations d_A, d_B, and d_C to it randomly, the resulting points will be dense in the Sierpinski triangle, so the following algorithm will again generate arbitrarily close approximations to it:^[3]

Start by labeling p₁, p₂ and p₃ as the corners of the Sierpinski triangle, and a random point v₁. Set v_n+1 = 1/2(v_n + p_rn), where r_n is a random number 1, 2 or 3. Draw the points v₁ to v_∞. If the first point v₁ was a point on the Sierpiński triangle, then all the points v_n lie on the Sierpinski triangle. If the first point v₁ to lie within the perimeter of the triangle is not a point on the Sierpinski triangle, none of the points v_n will lie on the Sierpinski triangle, however they will converge on the triangle. If v₁ is outside the triangle, the only way v_n will land on the actual triangle, is if v_n is on what would be part of the triangle, if the triangle was infinitely large.

Animated construction of a Sierpinski triangle. https://handwiki.org/wiki/index.php?curid=1891558

Or more simply:

1. Take three points in a plane to form a triangle, you need not draw it.
2. Randomly select any point inside the triangle and consider that your current position.
3. Randomly select any one of the three vertex points.
4. Move half the distance from your current position to the selected vertex.
5. Plot the current position.
6. Repeat from step 3.

This method is also called the chaos game, and is an example of an iterated function system. You can start from any point outside or inside the triangle, and it would eventually form the Sierpinski Gasket with a few leftover points (if the starting point lies on the outline of the triangle, there are no leftover points). With pencil and paper, a brief outline is formed after placing approximately one hundred points, and detail begins to appear after a few hundred. An interactive version of the chaos game can be found here.

1.4. Arrowhead Curve

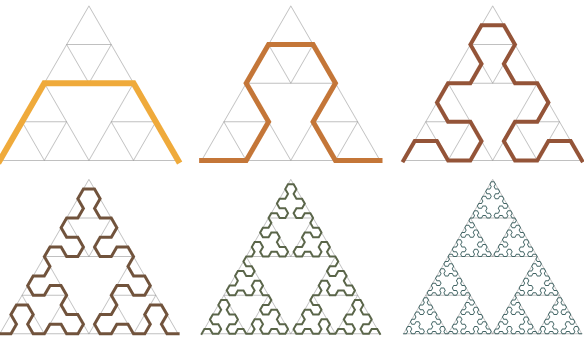
Another construction for the Sierpinski triangle shows that it can be constructed as a curve in the plane. It is formed by a process of repeated modification of simpler curves, analogous to the construction of the Koch snowflake:

1. Start with a single line segment in the plane
2. Repeatedly replace each line segment of the curve with three shorter segments, forming 120° angles at each junction between two consecutive segments, with the first and last segments of the curve either parallel to the original line segment or forming a 60° angle with it.

The resulting fractal curve is called the Sierpiński arrowhead curve, and its limiting shape is the Sierpinski triangle.^[4] Actually the aim of the original article by Sierpinski of 1915, was to show an example of a curve (a Cantorian curve), as the title of the article itself declares.^[5][6]

1.5. Cellular Automata

The Sierpinski triangle also appears in certain cellular automata (such as Rule 90), including those relating to Conway's Game of Life. For instance, the Life-like cellular automaton B1/S12 when applied to a single cell will generate four approximations of the Sierpinski triangle.^[7] A very long one cell thick line in standard life will create two mirrored Sierpinski triangles. The time-space diagram of a replicator pattern in a cellular automaton also often resembles a Sierpinski triangle, such as that of the common replicator in HighLife.^[8]

1.6. Pascal's Triangle

If one takes Pascal's triangle with 2ⁿ rows and colors the even numbers white, and the odd numbers black, the result is an approximation to the Sierpinski triangle. More precisely, the limit as n approaches infinity of this parity-colored 2ⁿ-row Pascal triangle is the Sierpinski triangle.^[9]

1.7. Towers of Hanoi

The Towers of Hanoi puzzle involves moving disks of different sizes between three pegs, maintaining the property that no disk is ever placed on top of a smaller disk. The states of an n-disk puzzle, and the allowable moves from one state to another, form an undirected graph, the Hanoi graph, that can be represented geometrically as the intersection graph of the set of triangles remaining after the nth step in the construction of the Sierpinski triangle. Thus, in the limit as n goes to infinity, this sequence of graphs can be interpreted as a discrete analogue of the Sierpinski triangle.^[10]

2. Properties

For integer number of dimensions d, when doubling a side of an object, 2^d copies of it are created, i.e. 2 copies for 1-dimensional object, 4 copies for 2-dimensional object and 8 copies for 3-dimensional object. For the Sierpinski triangle, doubling its side creates 3 copies of itself. Thus the Sierpinski triangle has Hausdorff dimension ^log(3)/_log(2) = log₂ 3 ≈ 1.585, which follows from solving 2^d = 3 for d.^[11]

The area of a Sierpinski triangle is zero (in Lebesgue measure). The area remaining after each iteration is clearly 3/4 of the area from the previous iteration, and an infinite number of iterations results in zero.^[12]

The points of a Sierpinski triangle have a simple characterization in barycentric coordinates.^[13] If a point has coordinates (0.u₁u₂u₃…, 0.v₁v₂v₃…, 0.w₁w₂w₃…), expressed as binary numerals, then the point is in Sierpinski's triangle if and only if ui + vi + wi = 1 for all i.

3. Generalization to Other Moduli

A generalization of the Sierpinski triangle can also be generated using Pascal's triangle if a different Modulo is used. Iteration n can be generated by taking a Pascal's triangle with Pn rows and coloring numbers by their value for x mod P. As n approaches infinity, a fractal is generated.

The same fractal can be achieved by dividing a triangle into a tessellation of P² similar triangles and removing the triangles that are upside-down from the original, then iterating this step with each smaller triangle.

Conversely, the fractal can also be generated by beginning with a triangle and duplicating it and arranging n(n + 1)/2 of the new figures in the same orientation into a larger similar triangle with the vertices of the previous figures touching, then iterating that step.^[14]

4. Analogues in Higher Dimensions

A Sierpinski square-based pyramid and its 'inverse'. https://handwiki.org/wiki/index.php?curid=1455372

A Sierpiński triangle-based pyramid as seen from above (4 main sections highlighted). Note the self-similarity in this 2-dimensional projected view, so that the resulting triangle could be a 2D fractal in itself.

The Sierpinski tetrahedron or tetrix is the three-dimensional analogue of the Sierpinski triangle, formed by repeatedly shrinking a regular tetrahedron to one half its original height, putting together four copies of this tetrahedron with corners touching, and then repeating the process. This can also be done with a square pyramid and five copies instead.

A tetrix constructed from an initial tetrahedron of side-length L has the property that the total surface area remains constant with each iteration. The initial surface area of the (iteration-0) tetrahedron of side-length L is L²√3. The next iteration consists of four copies with side length L/2, so the total area is 4(L/2)²√3 = 4L²√3/4 = L²√3 again. Meanwhile the volume of the construction is halved at every step and therefore approaches zero. The limit of this process has neither volume nor surface but, like the Sierpinski gasket, is an intricately connected curve. Its Hausdorff dimension is log(4)/log(2) = 2. If all points are projected onto a plane that is parallel to two of the outer edges, they exactly fill a square of side length L/√2 without overlap.

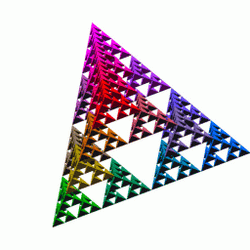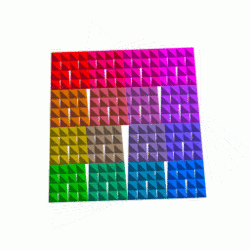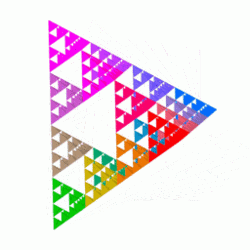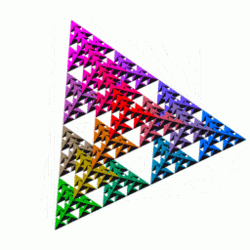
4.1. Numerical Generation

A short code in the Mathematica internal language: the recursive procedure SiPyramid generates a 3D pyramid of arbitrary order n as the displayable graphic object Graphics3D:

vect[1] = {0, 0, 0}; vect[2] = {1, 0, 0}; vect[3] = {0.5, 3^0.5/2, 0}; vect[4] = {0.5, 1/3*3^0.5/2, ((3^0.5/2)^2 - (1/3*3^0.5/2)^2)^0.5}; Tetron[{i_, j_, k_}] := Tetrahedron[{vect[1] + {i, j, k}, vect[2] + {i, j, k}, vect[3] + {i, j, k}, vect[4] + {i, j, k}}]; SiPyramid[0, {i_, j_, k_}] := {Tetron[{i, j, k}]}; SiPyramid[n_, {i_, j_, k_}] := Module[{s = {}}, Do[s = Union[s, SiPyramid[n - 1, 2^(n - 1)*vect[u] + {i, j, k}]], {u, 4}]; s];

File:Sierpinski tetrahedrons.stl

5. History

Wacław Sierpiński described the Sierpinski triangle in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral of Anagni, Italy,^[15] and other places of central Italy, for carpets in many places such as the nave of the Roman Basilica of Santa Maria in Cosmedin,^[16] and for isolated triangles positioned in rotae in several churches and basilicas.^[6][17] In the case of the isolated triangle, the iteration is at least of three levels.

A medieval triangle, with historically certain dating ^[6] has been studied recently. It is in porphiry and golden leaf, isolated, level 4 iteration

The Apollonian gasket was first described by Apollonius of Perga (3rd century BC) and further analyzed by Gottfried Leibniz (17th century), and is a curved precursor of the 20th-century Sierpiński triangle.^[18]

6. Etymology

The usage of the word "gasket" to refer to the Sierpinski triangle refers to gaskets such as are found in motors, and which sometimes feature a series of holes of decreasing size, similar to the fractal; this usage was coined by Benoît Mandelbrot, who thought the fractal looked similar to "the part that prevents leaks in motors".^[19]