The techno-economic analysis (TEA) and the life cycle cost analysis (LCCA) are the most widely used approaches for modeling and calculating processes’ economic impacts. A simulation-based TEA is a cost-benefit analysis that simultaneously considers technical and economic factors. In addition, the method facilitates the development of the entire project and provides a systematic approach for examining the interrelationships between economic and technological aspects. When it comes to economic studies, it is intimately bonded with uncertainty. There are numerous uncertainty sources, classified in various ways. The uncertainty reflects “an inability to determine the precise value of one or more parameters affecting a system.” The variability refers to the different values a given parameter may take. This implies that a probability density function (PDF), for instance, can be employed to estimate and quantify the variability of a given parameter. The bias refers to “assumptions that skew an analysis in a certain direction while ignoring other legitimate alternatives, factors, or data.”
1. Techno-Economic Analysis
Generally, a
techno-economic analysis (TEA
) compares costs and benefits by examining technological and economic aspects
[1]. TEA combines engineering design and process modeling with economic evaluation, providing a means of assessing the economic viability of a process. From another perspective, TEA is a method of estimating a plant’s performance, emissions, and cost in advance of its construction. A variety of definitions of evaluation methods are presented in the literature, most of which differ in terms of the evaluation scope and level of detail. TEA was offered not only as a tool in which investment and performance analysis converge but also as an appropriate approach for integrating engineering design and process modeling with the economic aspects
[1][2][1,18].
Despite the significant increase in the use of TEA, in the absence of an agreed upon definition, it is difficult to determine what constitutes a TEA
[3][19]. However, researchers have attempted to define the methodology of TEA. Kuppens et al.
[4][17] discussed that three key questions need to be answered by a TEA: What is the mechanism of the technology? Does the technology have profit potential? How desirable is the technology? Nevertheless, they defined TEA as a combination of economic and technical evaluations. There are still some methodological guidelines that need to be clarified despite the effectiveness of the provided definition. In addition, the NABC (National Advanced Biofuels Consortium) provided a detailed description of the purpose of TEA in order to determine the financial viability of a conversion strategy. As part of TEA, engineering design, process modeling, and economic evaluation are integrated.
Appendix A provides some definitions and statements of TEA.Before delving into existing uncertainty analysis methodologies, offering a general overview of techno-economic models is useful since different investigations may necessitate different uncertainty analysis techniques. Van der Spek et al.
[5][3] summarized the types of uncertain parameters based on the model complexity (simple, moderate, and complex). For simple models, uncertain parameters include financial parameters such as lifetime, discount rate, fuel and consumables costs, and scaling exponents. In moderate systems, uncertain parameters include simple model parameters, equipment sizes, equipment costs, and escalation factors. In addition, uncertain parameters include scaling factors, detailed capital costs, operational costs, and simple and moderate parameters in complex models. Giacomella
[1] reported that the TEA’s methodological steps could be categorized into the following six steps: (1) defining technology readiness levels (TRL), (2) system elements and boundaries identification, (3) Analyzing market conditions, costs, and feasibility, (4) profitability analysis, (5) analysis of risk and uncertainty using sensitivity and scenario forecasting, and (6) recommendations.
2. Life Cycle Cost Analysis
Life cycle cost analysis (LCCA) is a technique used to evaluate all relevant expenses of a project, product, or measure over its time. LCCA takes into account all costs, including initial costs (such as capital investment, purchase, and installation), future costs (such as energy, operating, maintenance, capital replacement, and financing costs), and any resale, salvage, or disposal costs, over the lifetime of the project or product
[6][7][8][9][20,21,22,23]. Compared to TEA, LCCA relies on a broader regulatory foundation. The LCCA may depend on a broader set of legal regulations, standards, and guidelines than the TEA, whose primary sources are individual guidelines and intellectual debate
[1]. The European Union recognizes LCCA through its directives (2014/24/EU
[10][24], 2014/25/EU
[11][25]), and several product-specific standards have been developed for the oil and gas and construction industries. (ISO 15663:2000 and 15686:2017, respectively).
In the literature, LCCA is also described in several different ways, but it appears to have a higher degree of coherence than TEA.
As obtained from definitions in Appendix A, LCCA facilitates the proper decision-making process by aggregating and estimating costs into easy-to-read figures, as well as revealing and counting the influence of different factors, such as the time value of money and other uncertain economic factors, on decisions. The cost generally includes all costs related to production, operation, maintenance, and retiring/disposing of a product from the cradle to the grave.
Uncertainty in parameters, such as cash flows and their timing, interest rates, and duration analysis, are the most commonly reported uncertainty sources in LCCA. The uncertainty of cash flow is called cash flow unpredictability
[12][26]. The uncertainty of interest rates results from fluctuating economic conditions and markets, and the change of interest rates over time puts uncertainty into any study
[13][14][27,28]. The literature addresses uncertainty in describing the cash flows’ timing using the same reasoning that applies to interest rates and cash flows.
According to the literature
[1][15][16][1,29,30], the TEA’s methodological steps can be categorized into the following five steps: (1) problem definition and objectives, (2) cost analysis, (3) discounting future cash flows and economic evaluation, (4) considering risks and uncertainties, and (5) comparing the alternatives and possibilities.
3. Uncertainty
According to Finnveden et al.
[17][31], uncertainty is defined as the deviation between a quantity measured or calculated and its true value and discussed many reasons to make the uncertainty happen. Different variables influence how decision-makers interpret uncertain outcomes, including their preferences, timing, and scenario framing
[18][32]. In the literature, sources of uncertainty, such as data, choices, and relations, are distinguished from types of uncertainty. As examples of uncertainty types, data variability, inconsistency between alternative products, and an incorrect relationship between pollutant emissions and their environmental impact can be cited.
[19][33]. From the literature, an overview of different types of uncertainty and their definitions is given in
Table 1. As seen, 26 different types of uncertainty were listed and defined. The most significant types of uncertainty in TEA and LCCA are model, parameter, and scenario uncertainties, as well as variability
(see Section 4). Over time, different methods have been developed to deal with different types of uncertainty. Uncertainty modeling can be used to reduce, evaluate, and demonstrate uncertainty. These methods can be classified into four groups: deterministic, probabilistic, possibilistic, and other methods
[20][34]. In another classification, these methods were categorized into quantitative and qualitative techniques
[21][35]. Barahmand et al.
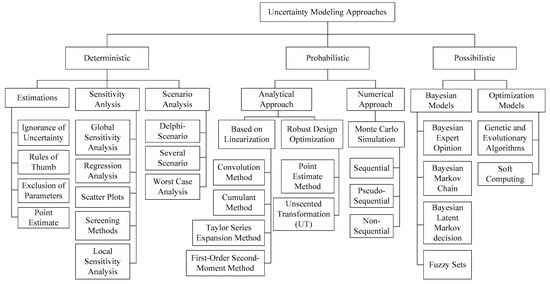
[22][36] reported another classification which consists of possibilistic, probabilistic, hybrid possibilistic-probabilistic, interval-based analysis, robust optimization, and information gap decision theory. A diagram illustrating well-known methods of dealing with various types of uncertainty is shown in
Figure 1 (based on
[20][23][34,37]).
Figure 1.
Classification of different methods to cope with system uncertainties.
Table 1.
Overview of different types and sources of uncertainty.
| Type |
Source |
Ref. |
| Variability |
An unpredictable result of changes in systems (involving time, space, or other variables) |
[24][38] |
| Systematic errors |
Bias in sampling procedures or measuring equipment |
[24][38] |
| Measurement error |
Errors that appear random due to imperfections in the measurement equipment and observational methods |
[24][38] |
| Random errors |
A measurement error caused by varying factors between measurements |
Oxford definition |
| Parameter uncertainty |
Measurement errors, sampling errors, variability, and surrogate data contribute to incomplete knowledge of parameters |
[25][39] |
| Model uncertainty |
Our limitations in representing physical systems may result in uncertainty when we approximate a model in order to solve a problem. |
[24][38] |
| Scenario uncertainty |
A level of uncertainty associated with specifying an exposure scenario that is consistent with the purpose and scope of the exposure assessment |
[26][40] |
| Exposure factor Uncertainty |
Contributes to the specification of numerical values for human exposure |
[26][40] |
| Uncertainty due to choices |
Different choices of partitioning methods, etc. |
[27][41] |
| Spatial variability |
The phenomenon occurs when the value of a quantity is different at different spatial locations. A descriptive spatial statistic such as the range can be used to assess spatial variability. |
[28][42] |
| Temporal variability |
A measure of the frequency and magnitude of fluctuations in ecosystem structure such as standing stocks of resources and species abundance |
[29][43] |
| Data uncertainty |
This type of data contains noise that causes it to deviate from the correct or original values. |
[30][44] |
| Completeness uncertainty |
Like modeling uncertainties, completeness uncertainties occur at the beginning of the probabilistic risk analysis process. In probabilistic risk analysis, there is uncertainty as to whether all significant phenomena and significant relationships have been considered. |
[31][45] |
| Aleatory uncertainty |
Samples and parameters are intrinsically random |
[24][38] |
| Epistemic uncertainty |
An insufficient understanding of fundamental phenomena |
[24][38] |
| Ambiguity |
Being open to multiple interpretations |
Oxford definition |
| Volitional uncertainty |
Whether or not an individual will follow through on an individual’s commitment |
[32][46] |
| Statistical variation |
A measure of how widely distributed a group of data is |
[33][34][47,48] |
| Subjective judgment |
A lack of certainty in the interpretation of data or the estimations of experts |
[24][38] |
| Linguistic imprecision |
Depends on the utterance alternatives available to the speaker in the context |
[35][49] |
| Inherent randomness |
Resulting from the irreducibility of a system to a deterministic system |
[24][38] |
| Disagreement |
Lack of consensus or approval, inconsistency or correspondence |
Oxford definition |
| Approximation |
Nearly accurate but not exactly correct value or quantity |
Oxford definition |
| Semantic uncertainty |
Occurs when humans give names to things, especially when those things are mapped as geographic data |
[36][50] |
| Interpretational uncertainty |
Occurs when interpreters use inconsistent decoding methodologies to extract information from data or models. |
Helmholtz dictionary |