1. History

Inoue Dōsetsu Inseki, the fourth head of the Inoue house and Meijin from 1708 to his death in 1719, is best known for his role as guardian of the young Dōchi after the death of his master Dōsaku;^[1] his exceptional skill as a composer of go problems was only discovered after the collapse of the Four go houses from 1868, during the Meiji Restoration.^{[N 1]}

In 1713, Dōsetsu compiled Igo Hatsuyōron from a collection of more than 1500 problems, many of which were composed by him or improved from previous problems.^[2] The book is designed to serve the training of the best disciples, and to this end contains only the problems, without any indication on their solution.^{[N 2]} For more than 150 years, it was kept secret, being studied only one problem at a time, under the direct control of the Inoue house; the very existence of the book was ignored by the other three houses (Hon'inbō, Hayashi and Yasui).^[2]

The Hatsuyōron became public after 1868 (passing from hand to hand in the Hon'inbō house),^[2] and a first edition is published in 1914 by Hon'inbō Shūsai, enriched with solutions and comments; from that moment, the book acquired its reputation of the "most difficult collection of go problems".^[3] Two other editions, mostly from Shūsai’s, but improving and detailing the solutions, appeared in 1953 (under the direction of Hideyuki Fujisawa) and in 1980 (under the direction of Utaro Hashimoto). These editions, however, are based not on the original manuscript (which is thought to have been destroyed in a fire),^[2] but on incorrect copies, into which some problems from Xuanxuan Qijing (the oldest Chinese classics) slipped.

In 1982, Araki Naomi discovered a previous copy^[4] apparently containing only the problems of the original version, including two previously unknown; the responsibility of a new edition was entrusted to Hideyuki Fujisawa (then Kisei), which caused him to look more closely at one of these two problems (the number 120), to conclude that this is "The most difficult problem ever composed"; he publishes an article on this subject,^[5] detailing the remarks of the complete edition.

From 1988, an analysis of the solutions of the 1982 edition by Chinese professionals led them to question some of the Japanese conclusions; Cheng Xiaoliu^{[N 3]} published in 2010 a revised edition of their comments, under the title of Wéiqí Fāyánglùn Yánjiū (围棋 发 阳 论 研究, Research on Hatsuyōron).^[6]

2. Content

The exact initial composition of the collection is unknown, and the order of the problems is probably corrupt; Cheng Xiaoliu noted that in the edition of 1914, the first problem has no solution,^{[N 4]} and suggests that it could have been placed in first position by some rival school, to discredit the book.^[7]

The copy used in the 1982 edition, however, is considered fairly close to the original work composed by Dōsetsu,^[2] and also contains a written postface by his hand, in which he explains in particular the meaning of the title of the collection and how it should be studied;^{[N 2]} this copy contains 183 problems, divided into six sections:^{[N 5]}

• live (30 problems);
• kill (46 problems, among which 13 problems of sacrifice of blocks (nakade and ishinoshita) grouped at the end of section);
• ko battles (51 problems);
• capturing races (semeai) (36 problems);
• ladders (shichō^{[N 6]}) (12 problems);
• various problems (8 problems).

Most of these problems (except perhaps those of the last two sections) can be considered life and death problems; the Hatsuyōron does not deal with issues of strategy, but only aims to develop the capacity of tactical play.^{[N 2]} These problems, however, are not "realistic" in the sense that they would come from situations that can be met in a real game; they seek above all to show extraordinary moves and maneuvers, and to force one to envisage well-hidden resistances; moreover, one of the conventions chosen for these problems is that "all the stones of the initial setting must be useful",^{[8][N 7]} which Dōsetsu sometimes exploits for additional artistic effects, as displayed by the example of problem 43.

Almost all these problems are at the level of professional players (and are still used in their training),^[2] that is to say that an amateur player cannot solve them in a game situation, without the mental aid of laying stones on the board; some of them are so difficult that they are probably insoluble under these conditions, even by the best players; this is particularly the case of the seven problems covering the entire goban, including the astonishing problem 76, which he gives the title "the bait catches the fish".^[9]

3. The Most Difficult Problem Ever Composed

 

Igo Hatsuyōron 120- black to play and win.

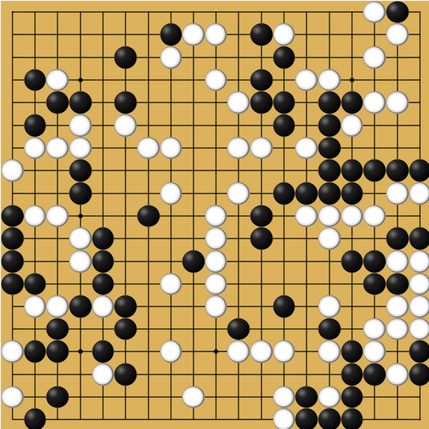
In 1982, a copy from the 19^th century was found, containing two problems not included in previous editions.^[4] The manuscript was entrusted to Fujisawa Hideyuki (then Kisei) to make a new edition commented on it, but, assuming that the problem 120 had been copied badly, he handed it over to one of his disciples, Yasuda Yasutoshi, to try to rectify it.^[10] He finally saw the unprecedented sacrifice maneuver which is the main theme of the problem, and after about a thousand hours of collective work,^{[N 8]} Fujisawa believed that the problem is solved, and published its solution, translated in GB World number 29 under the title The Most Difficult Problem Ever, accompanied by a complimentary comment, mentioning "the surprising novelty of the theme and forms, the precise calculation of the fights, and the delicate balance of trade and score, all of which make this unique problem the masterpiece of a lifetime".^[11]

The statement of the problem (figure on the right) is a position that could almost be drawn from a real game, accompanied by the caption "Black plays and wins the game";^{[N 9]} the solution is, in the main variant, a long series of battles using tactics unthinkable even for professional players, containing in particular a sacrifice of twenty black stones that White is obliged to refuse as long as possible,^{[N 10]} and completing, after more than one hundred and fifty moves, end-game subtleties (yose) finally ending in a Black victory by one or two points.^[12]

This analysis is not disputed by the Chinese edition of Hatsuyōron in 1988, although this edition contains an improvement of the main sequence, bringing the margin of Black's victory to three points. But in 2005, a German amateur player, Joachim Meinhardt, discovered an unexpected resistance of White^[4] confirmed by professionals,^{[N 11]} this line of play questions all previous solutions. At the end of 2007, another German amateur, Thomas Redecker, observed that a seemingly mediocre play by Black, which had never been envisaged until then, played at the opportune moment (at move 67) of the main variant), perhaps allows the situation to be saved and decided to publish all of the analyses on a website, later in the form of a book.^[13] They are enriched (first with the help of a wiki)^[14] by many amateur and professional players, and a winning line for Black was confirmed by professional players starting in 2012, but, in 2015, new variations appeared again;^[14] the problem cannot therefore be considered as completely resolved.^{[N 12]}

From 2016 onwards, the spectacular progress in artificial intelligence led some optimistic amateurs to believe that a solution could be obtained by computer, but attempts in this direction were disappointing until 2019.^[15] However, in October 2019, a significant improvement in the deep learning techniques used made it possible to discover new variations based on moves never before envisaged, showing that a definitive solution has still not been reached.^[16]

4. Notes and References

Notes

References