Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Camila Xu and Version 1 by Vladimir Kindra.
The use of combined cycle gas turbine (CCGT) plants allows the most efficient conversion of the chemical heat of fossil fuels for generating electric power. In turn, the combined cycle efficiency is largely dependent on the working flow temperature upstream of a gas turbine.
- thermodynamic analysis
- net efficiency
- turbine
1. Promising Methods to Increase the CCGT Plant Efficiency
Natural gas is currently one of the most common types of fuels: it accounts for about 23.6% of the total structure of electricity generation [1]. The most efficient conversion of the chemical energy of natural gas into electrical power is carried out by CCGT plants, in which most components of the working flow are combustion products of the air-and-fuel mixture (Brayton cycle) and water steam (Rankine cycle). The net electric efficiency of advanced CCGT plants exceeds 63%.
High efficiency figures, in particular, are demonstrated by CCGT using SGT5-9000HL gas turbine plants from Siemens, with the working flow temperature upstream of such plants being about 1550 °C and an exhaust gas temperature of 670 °C. In Russia, GTE-160 gas turbine plants are widely used, but they feature a significantly lower initial temperature of the working flow, of about 1100 °C, and an exhaust gas temperature equal to 537 °C. The net efficiency of these GTPs in a free running mode reaches 34.4%, and when operated as part of the CCP-220T CCGT power plant, it reaches 50.4%.
The most obvious method to increase the CCGT efficiency is increasing the working flow temperature upstream of the gas turbine. However, for this method to be implemented, weit is needed to develop high-temperature technology for electric power generation [2,3][2][3].
An alternative way to increase the CCGT plant efficiency (by 2–3%) consists of the useful application of low-potential heat sources [4,5,6][4][5][6]. In particular, it is possible to add the organic Rankine cycle to CCGT plants for a deeper utilization of the exhaust gas heat or for decreasing the cold source temperature [7,8,9][7][8][9]. However, most heat carriers in low-temperature cycles (first of all, freons) are characterized by lower availability and chemical compound stability, as well as higher toxicity as compared to water. Besides, adding one more cycle entails an increase in capital costs for the power facility. The combination of the above factors was the main reason for the lack of widespread use of this technology [10,11][10][11].
2. Replacing the Water Stream Circuit with Carbon Dioxide for CCGT Plants
A promising method to increase the heat efficiency and to reduce the cost of power plants is the use of carbon dioxide as the working flow that works at supercritical parameters, which allows implementation of the Brayton cycle with low costs for auxiliary needs at a moderate initial temperature and compact dimensions of the main power equipment [12,13,14][12][13][14]. Today, at least five variations of carbon dioxide cycles are known [15,16,17][15][16][17]. The reasons why researchers worldwide are interested in this technology are largely related to the advantages of carbon dioxide as compared to other heat carriers.
In particular, carbon dioxide heat carriers feature low values of critical temperature (30.98 °C) and pressure (7.38 MPa). The low critical temperature of carbon dioxide, being close to the ambient temperature, makes it possible to compress the working flow near the saturation line [18[18][19],19], which reduces the compressor workload and the temperature of heat removal from the cycle without condensation of the working flow. In addition, carbon dioxide has a relatively low aggressiveness as compared to water and shows its corrosive activity only in the presence of moisture in gas or a water film on the metal surface. The price of carbon dioxide gas is comparable to that of the water heat carrier.
Long-term thermodynamic studies of S-CO2 power facilities resulted in the development of the five cycles presented in Figure 1. The simplest S-CO2 cycle is a closed Brayton cycle with the heat utilization of the exhaust gases (Figure 1a). It contains a compressor (C), regenerator (RH), reactor (R), turbine (T), electricity generator (G), and pre-cooler (PC). The S-CO2 Brayton cycle with reheating is shown in Figure 1b. Here, the turbine consists of a high-pressure turbine (HPT), and a low-pressure turbine (LPT). The S-CO2 Brayton cycle with intermediate cooling is presented in Figure 1c. The introduction of intermediate cooling allows for an increase in the cycle efficiency due to a reduction in the compressor’s energy consumption. The S-CO2 Brayton cycle with partial cooling is presented in Figure 1d. It differs from the simplest S-CO2 Brayton cycle (Figure 1a) by application of a cooler (CR), pump (P), recompressing compressor (RC), high-temperature regenerator (HTR), and low-temperature regenerator (LTR). The use of partial cooling together with two sections of regenerators improves the regeneration system’s efficiency.
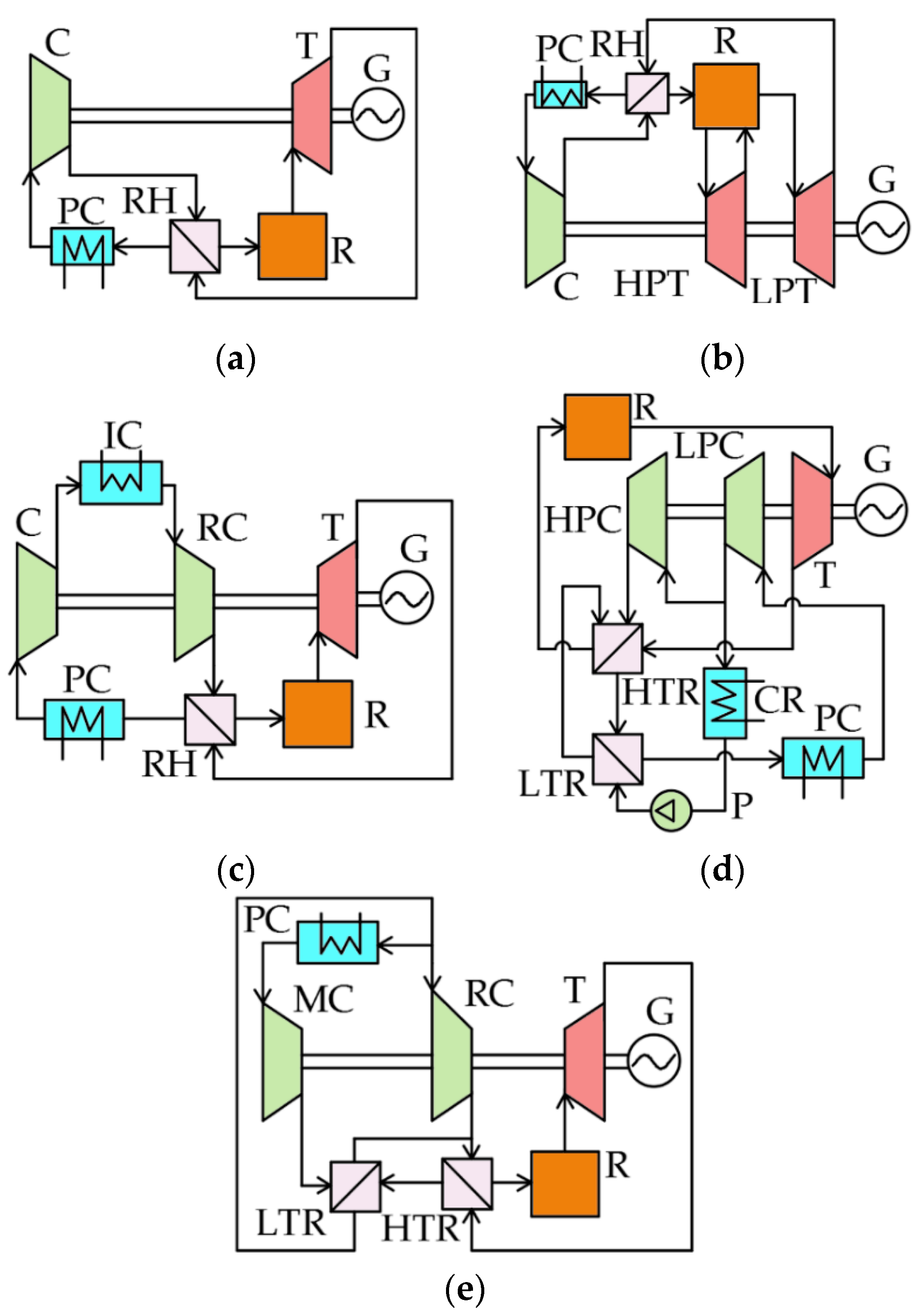
Figure 1. Supercritical CO2 Brayton cycles: (a) S-CO2 Brayton cycle with regeneration; (b) S-CO2 Brayton cycle with reheating; (c) S-CO2 Brayton cycle with intermediate cooling; (d) S-CO2 Brayton cycle with partial cooling; (e) S-CO2 Brayton cycle with recompression. C—compressor, RH—regenerator, R—reactor, T—turbine, G—electricity generator, PC—pre-cooler, HTP—high-pressure turbine, LPT—low-pressure turbine, CR—cooler, P—pump, RC—recompressing compressor, HTR—high-temperature regenerator, LTR—low-temperature regenerator, MC—main compressor, and IC—intermediate cooler.
With the initial working flow temperature of 550 °C, the most effective is the Brayton cycle using supercritical CO2 with recompression. Its net efficiency is 47.3% [20]. However, it should be noted that all the cycles under consideration are characterized by a high initial temperature of heat supply, which will certainly have a negative impact on the efficiency of the waste heat boiler. In this connection, additional measures are required to reduce the temperature of gases released into the atmosphere.
Many scientific studies consider combined plants with several sequential carbon dioxide recovery cycles [20,21][20][21]. Thus, the paper [21] assesses the impact of the heat circuit in heat recovery cycles on the efficiency of a combined plant operating based on Siemens SCC5-4000F. The exhaust gas temperature of this GTP is about 580 °C. The above research has established that one of the most effective options is using circuits with the recompression Brayton cycle and the Brayton cycle with partial heating; in this case, the net efficiency of a combined plant reaches 57.9%. At the same time, this restudy dearch does not include a full optimization of the basic thermodynamic parameters, whereas the analysis of initial temperatures is little relevant for the domestic power sector.
3. Current State of Research on Carbon Dioxide Cycles
In the modern literature, one can find many modifications of the considered basic configurations of the Brayton supercritical carbon dioxide cycle, which allow for increasing the efficiency of the power unit and expanding the applicability range [22,23][22][23]. One of the most attractive directions is the usage of the Brayton cycle with liquefied natural gas (LNG). Advantages of this technology are described in the work [24]. In particular, the use of liquefied natural gas increases the attractiveness of energy resources for maritime transport, which is relevant for plants operating in coastal areas. In addition, the use of liquefied natural gas could be used as a cooling stream. Therefore, it is advisable to use the heat generated at low potential sources, which significantly increases the efficiency of the Brayton cycle. According to the presented research results, the cycle efficiency could be equal to 52% at an inlet gas temperature of 550 °C. At the same time, the main disadvantages of this scheme are the narrow application range (it can be used only near a regasification terminal) and the expensiveness of LNG technology (it is more than twice as expensive as pipeline natural gas). Due to the low boiling point of carbon dioxide at atmospheric pressure, the use of trigeneration cycles (plants producing heat, power, and chilled water for air conditioning or refrigeration), is becoming relevant. Particularly, the article [25] states that the advantage of trigeneration cycles is the high efficiency of the power unit up to 78% (heat cold and power energy are considered to be of equal value in calculations). The main disadvantages of this design are high complexity, poor maneuverability, and high capital costs due to additional compressor technology and heat exchangers. The use of a pump compression process is more effective than the use of a compressor. In work [26], the Brayton cycle with condensation of heat carrier using acetone to dissolve carbon dioxide is considered. After compression in the compressor, the carbon dioxide is cooled down and dissolved in acetone. The mixture is then compressed by a pump, the carbon dioxide is separated, heated in a regenerator, and heated in a heater. Then supercritical CO2 is expanded in the turbine and cooled in the regenerator. The cycle efficiency is 56% at the turbine inlet temperature of 1400 °C. It is worth noting that the modifications considered earlier lead to an increase in capital costs and technological complexity of the power unit. Therefore, the use of these solutions will negatively affect the payback period, reliability, and maneuverability of the combined cycle unit. Thus, it was decided to use the simple supercritical CO2 Brayton cycle with recompression and the basic option, allowing efficient utilization of low-potential heat.4. Approaches to Energy Cycle Optimisation
Determination of the power cycle optimum parameters requires the definition of the target function, the variables, and the way of optimization. The main target function for optimization is efficiency. The main variable parameters usually are pressures and temperatures. In turn, the optimization approaches can be divided into three main categories. Firstly, there is the equation-oriented approach. In this approach, the optimization problem and the simulation problem are solved simultaneously since the model equations are included as constraints in the problem. Thus, there is no distinction between independent and dependent variables or between model equations and technical-economic constraints. As a rule, the resulting optimization problem is solved by means of gradient-based algorithms using quadratic programming. It is worth noting that due to the large number of variables the algorithm may return local minima or even an unallowable solution if the first iterative point is far from the real value [27]. A second way to optimize energy cycles is to apply a black-box approach. In this approach, the optimization algorithm examines the space of independent design, and, for each sample solution, the simulation program develops a cycle diagram, outputting the power unit performance. The main advantage of the black-box approach is the higher probability of determining the global optimum, as the optimization only considers the independent variables and specification constraints that are hidden in the computational model. Another advantage of this approach is the ability to introduce corrective design variables to resolve potential inconsistencies. However, the black-box method has the disadvantage of omitting modeling constraints and transition conditions that are not obvious from the specification [28]. A final, common, way to optimize thermal schemes is to use the infeasible path approach. This model consists of a set of black boxes in which some equations are “open” and are included in the algorithm as constraints. To speed up the convergence of the target function in closed loops, the “open” equations are disabled (e.g., in the so-called “recycling equations” related to the recirculation of material and energy flows, as in the case of a recuperator), provided the desired accuracy is achieved. Thus, the main advantage is saving the computing time required for each black-box evaluation. On the other hand, the intermediate solutions chosen by the optimization algorithm are generally inadmissible since they do not satisfy the open constraints and feasibility is only guaranteed when the optimization algorithm achieves convergence. Furthermore, in addition to the independent decision variables, additional auxiliary variables (called “gap variables”) need to be optimized, which increases the computation time of the optimization algorithm [29]. Due to the aforementioned advantages, such as simplicity and relative convergence accuracy, this research will use the black-box approach, which is widely used in energy cycle optimization [28]. On the other hand, due to the complex equations modeling the cycle components, the resulting performance figures returned by the solver may be noisy and unsmooth.References
- World Energy Balances—International Energy Agency. Available online: https://www.iea.org/data-and-statistics/data-product/world-energy-balances (accessed on 1 August 2022).
- Uvarov, A.; Antonova, A.; Vorobjev, A. The Analysis of Initial Parameters of Steam in the Combined-Cycle Plant with High Temperature Gas Turbine. MATEC Web Conf. 2015, 37, 01062.
- Rogalev, A.; Komarov, I.; Kindra, V.; Osipov, S. Methods for Competitiveness Improvement of High-Temperature Steam Turbine Power Plants. Inventions 2022, 7, 44.
- Vélez, F.; Segovia, J.J.; Martín, M.C.; Antolín, G.; Chejne, F.; Quijano, A. A technical, economical and market review of organic Rankine cycles for the conversion of low-grade heat for power generation. Renew. Sustain. Energy Rev. 2012, 16, 4175–4189.
- Rogalev, N.; Kindra, V.; Komarov, I.; Osipov, S.; Zlyvko, O.; Lvov, D. Comparative Analysis of Low-Grade Heat Utilization Methods for Thermal Power Plants with Back-Pressure Steam Turbines. Energies 2021, 14, 8519.
- Rogalev, A.; Rogalev, N.; Kindra, V.; Zlyvko, O.; Vegera, A. A Study of Low-Potential Heat Utilization Methods for Oxy-Fuel Combustion Power Cycles. Energies 2021, 14, 3364.
- Cao, Y.; Mihardjo, L.W.; Dahari, M.; Tlili, I. Waste heat from a biomass fueled gas turbine for power generation via an ORC or compressor inlet cooling via an absorption refrigeration cycle: A thermoeconomic comparison. Appl. Therm. Eng. 2021, 182, 116117.
- Kindra, V.; Rogalev, N.; Osipov, S.; Zlyvko, O.; Naumov, V. Research and Development of Trinary Power Cycles. Inventions 2022, 7, 56.
- Braimakis, K.; Karellas, S. Energetic Optimization of Regenerative Organic Rankine Cycle (ORC) Configurations. Energy Convers. Manag. 2018, 159, 353–370.
- Sun, W.; Yue, X.; Wang, Y. Exergy Efficiency Analysis of ORC (Organic Rankine Cycle) and ORC-Based Combined Cycles Driven by Low-Temperature Waste Heat. Energy Convers. Manag. 2017, 135, 63–73.
- Shi, L.; Shu, G.; Tian, H.; Deng, S. A Review of Modified Organic Rankine Cycles (ORCs) for Internal Combustion Engine Waste Heat Recovery (ICE-WHR). Renew. Sustain. Energy Rev. 2018, 92, 95–110.
- Xu, J.; Liu, C.; Sun, E.; Xie, J.; Li, M.; Yang, Y.; Liu, J. Perspective of S−CO2 Power Cycles. Energy 2019, 186, 115831.
- Song, J.; Li, X.; Ren, X.; Gu, C. Performance Analysis and Parametric Optimization of Supercritical Carbon Dioxide (S-CO2) Cycle with Bottoming Organic Rankine Cycle (ORC). Energy 2018, 143, 406–416.
- Song, J.; Li, X.-S.; Ren, X.-D.; Gu, C.-W. Performance improvement of a preheating supercritical CO2 (S-CO2) cycle based system for engine waste heat recovery. Energy Convers. Manag. 2018, 161, 225–233.
- Dostal, V.; Hejzlar, P.; Driscoll, M.J. Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors. Ph.D. Thesis, MIT Center for Advanced Nuclear Energy Systems (CANES), Cambridge, MA, USA, 2004.
- Angelino, G. Real Gas Effects in Carbon Dioxide Cycles. In Gas Turbine Conference and Products Show; American Society of Mechanical Engineers: Cleveland, OH, USA, 1969; p. V001T01A071.
- Reyes-Belmonte, M.A.; Sebastián, A.; Romero, M.; González-Aguilar, J. Optimization of a recompression supercritical carbon dioxide cycle for an innovative central receiver solar power plant. Energy 2016, 112, 17–27.
- Rogalev, A.; Kindra, V.; Komarov, I.; Osipov, S.; Zlyvko, O. Structural and Parametric Optimization of S-CO2 Thermal Power Plants with a Pulverized Coal-Fired Boiler Operating in Russia. Energies 2021, 14, 7136.
- Liu, Y.; Wang, Y.; Huang, D. Supercritical CO2 Brayton Cycle: A State-of-the-Art Review. Energy 2019, 189, 115900.
- Cheng, W.-L.; Huang, W.-X.; Nian, Y.-L. Global Parameter Optimization and Criterion Formula of Supercritical Carbon Dioxide Brayton Cycle with Recompression. Energy Convers. Manag. 2017, 150, 669–677.
- Thanganadar, D.; Asfand, F.; Patchigolla, K. Thermal Performance and Economic Analysis of Supercritical Carbon Dioxide Cycles in Combined Cycle Power Plant. Appl. Energy 2019, 255, 113836.
- Invernizzi, C.M.; Iora, P. The exploitation of the physical exergy of liquid natural gas by closed power thermodynamic cycles. An overview. Energy 2016, 105, 2–15.
- Angelino, G.; Invernizzi, C.M. Carbon dioxide power cycles using liquid natural gas as heat sink. Appl. Therm. Eng. 2009, 29, 2935–2941.
- Qiang, W.; Yanzhong, L.; Xi, C. Exergy analysis of liquefied natural gas cold energy recovering cycles. Int. J. Energy Res. 2005, 29, 65–78.
- Bellos, E.; Tzivanidis, C. Parametric Analysis of a Polygeneration System with CO2 Working Fluid. Appl. Sci. 2021, 11, 3215.
- Li, X.; Huang, H.; Zhao, W. A supercritical or transcritical Rankine cycle with ejector using low-grade heat. Energy Convers. Manag. 2014, 78, 551–558.
- Walraven, D.; Laenen, B.; D’haeseleer, W. Optimum configuration of shell-and-tube heat exchangers for the use in low-temperature organic Rankine cycles. Energy Convers. Manag. 2014, 83, 177–187.
- Martelli, A.; Martelli, E.; Pierobon, L. Thermodynamic and technoeconomic optimization of Organic Rankine Cycle systems. In Organic Rankine cycle (ORC) Power Systems; Woodhead Publishing: Cambridge, UK, 2017; pp. 173–249.
- Biegler, L.; Cuthrell, J. Improved infeasible path optimization for sequential modular simulators—II: The optimization algorithm. Comput. Chem. Eng. 1985, 9, 257–267.
More
