You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 2 by Conner Chen and Version 1 by siddharth sinha.
Molecular Dynamics (MD) Simulations is increasingly used as a powerful tool to study protein structure-related questions. Starting from the early simulation study on the photoisomerization in rhodopsin in 1976, MD Simulations has been used to study protein function, protein stability, protein–protein interaction, enzymatic reactions and drug–protein interactions, and membrane proteins.
- molecular dynamics simulations
- enhanced sampling techniques
- membrane dynamics
1. Introduction
The essence of Molecular Simulations (MS) is a statistical mechanics and numerical method governed by the Newtonian laws of motion [1] for molecular properties, i.e., velocity, position, and energy, towards insights of molecular system while retaining macro-system physio-chemical properties. Two factors have promoted the increased application of molecular simulations over the years (Figure 1). One is the growing availability of experimentally determined protein structures, such as membrane proteins (ion channels, neurotransmitters and GPCRs etc.) [2[2][3],3], the other is the wide availability of graphics processing units (GPUs), which allows running simulations locally. MS typically analyses protein structure at a minimum of nano to micro-second time scale to reveal the dynamic nature of protein molecules covering a wide variety of biomolecular processes, such as conformational change, ligand binding and protein folding. Among the numerous approaches to MS, the Monte Carlo (MC) Simulation sampling method and the molecular Dynamics (MD) Simulation method are the two common methods. The basic concept of MCS is to generate an ensemble of conformation under specific thermodynamics conditions through stochastic approach; whereas the concept of MD Simulation is to iterate a time-dependent Newtonian equation of motions for hard sphere particles in a system [4,5][4][5], which can provide an ensemble of thermodynamic properties.
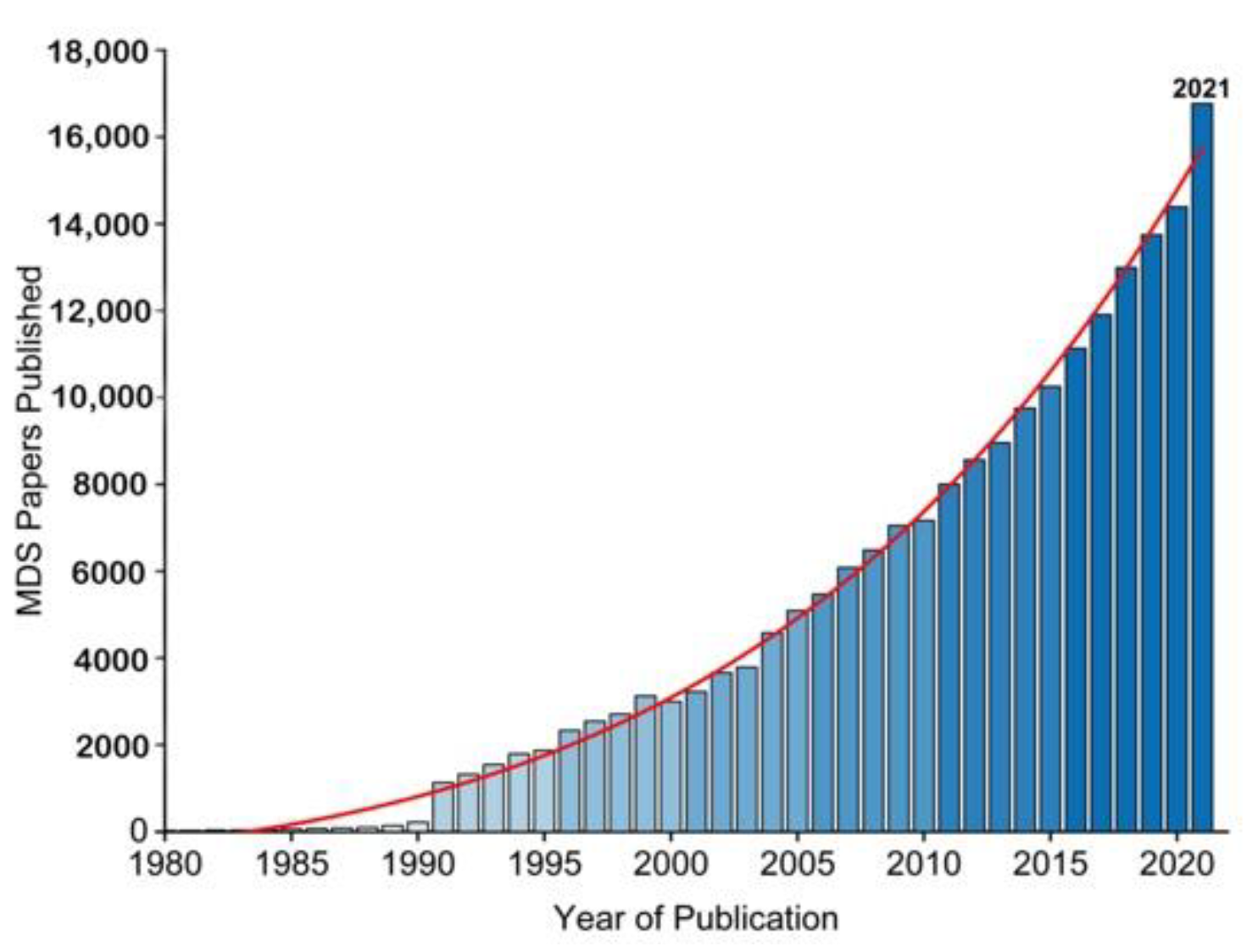
Figure 1. The growing use of MD Simulation studies over the years as reflected by publication (1980–2021). Data was from Web of Science.
2. A Brief History of Molecular Simulations
MS was first introduced in 1949 by Metropolis et al. to study particle interaction [6]. Metropolis proposed a probabilistic approach to approximate the “properties” of a set of particles [6]. Instead of treating particles as individuals, simulation was applied to measure the interactions of all particles until they reach equilibrium by the governing laws. Its success inspired the development of MS by Alder and Wainwright in 1959 [7]. The early MS algorithm used a rudimentary electronic computer to iterate atom collision. Each atom was assigned an initial velocity and position. Based on the elastic collision, the MS algorithm was applied to simulate attraction and repulsion of particles. In 1964, Rahman et al. published the first study in using MS to analyze liquid Argon [8]. The work demonstrated that MS was indeed possible to analyze Lennard Jones potential for interactions between Argon atoms. In 1971, Rahman and Stilinger reported their MS study on modelling liquid water, a system composed of molecules not just atoms [9]. Their work demonstrated that differing from its solid phases structure, liquid water consists of a random network of hydrogen bonds. In 1976, Warshel and Levitt expanded MS by integrating quantum mechanics and molecular mechanics (QM/MM) to study lysozyme reaction by proposing the exchange of the classical charge of atom i and j with quantum mechanics calculations [10]. In 1977, Karplus and collaborators first used MS to study protein by using constraint method to freeze out fast-degree freedom to reach longer simulation time [11,12][11][12]. Their study led to the Noble Prize in Chemistry awarded to Warshel, Levitt and Karplus in 2013 for the development of multiscale models for complex chemical systems [10]. Anderson et al. in 1980 used MS to sample the isoenthalpic (constant pressure) ensemble. Anderson’s solution to achieve constant pressure in MD Simulation sampling was to extend dynamic variable by including volume [13]. Parrinello and Rahman showed that the scheme can be generalized to include shape and volume fluctuations by using Lagrangian mechanics. This made it possible to study the issues such as crystallization and solid–solid phase transition [14]. Their idea of extending the system dynamic variables was to assume that the system exchanges energy with a fictitious pressure or temperature reservoir. Their method took into consideration the dielectric effect caused by the atomic polarizability and increased the accuracy of the binding site. In 1985, Car and Parrinello pioneered a scheme of combining MS with direct calculation of electronic structure by means of Density Function Theory (DFT). This work was important as it indicated the possibility of combining finite temperature into simulation for electronic structure calculations, which was not possible before [15]. During 1980s and 1990s, MS approach witnessed a rise in studies of condensed matter with growing access of enhanced computing power; further leading to the challenges of phase equilibria. Moreover, to address these challenges Panagiotopolus revised the MC algorithm, known as Gibbs ensemble Monte Carlo, to distinguish the phase equilibria approach that only require to simulate the involved phases but by-pass the interface [16]. Novel algorithms such as blue moon ensemble [17] hyper-MD [18] as well as advanced theoretical methods such as Nudged-Elastic Band [19] and String [20] were devised to address the challenges of time-scales (long-time dynamics of protein folding) and rare events. Further, the advancement in quantum programs outside chemistry field and the Noble prize in Chemistry 1998 being divided equally between Walter Kohn “for his development of density-function theory” and John A. Pople “for his development of computational methods in quantum chemistry” led to form a unified approach for molecular dynamics and density-function theory. Over the following years, time-dependent density-function theory (TDDFT) further enhanced the accuracy of large-scale simulations of excited state dynamics [21,22,23][21][22][23]. TDDFT-MD coupled simulations to simulate excited state dynamics of biomolecules and other nanostructures achieves high accuracy through utilizing small number of basic function thereby significantly reduced the memory requirements and computation time compared to plane-wave and real-space grid bases [24]. Furthermore, utilizing multiple computer processors in parallel for MD force calculations substantially enhanced with IBM’s Blue Matter code for its Blue Gene/L general-purpose supercomputer [25], resulting in improved parallel performances for the widely used MD platforms NAMD [26] GROMACS [27] AMBER [28]. Increasing innovation and with advent of GPU (Graphics processing units) and special-purpose processors such as Anton (parallel supercomputer to enable fast MD simulations) having computing power to perform up to 20 μs/day [29] further accelerated the simulation study in different biochemical processes. However, long-timescale simulations requires stringent force field (discussed in following section) compared with short-timescale simulations. To conclude this brief history of MS, it would be appropriate to remark that MS has clearly established itself as a key scientific instrument driven by enhanced computing power, fast and efficient algorithms and force fields (FF) are demonstrated by growing number of publications utilizing both experiments and simulation tools. Major breakthroughs over the years in MS studies are shown in Figure 2.
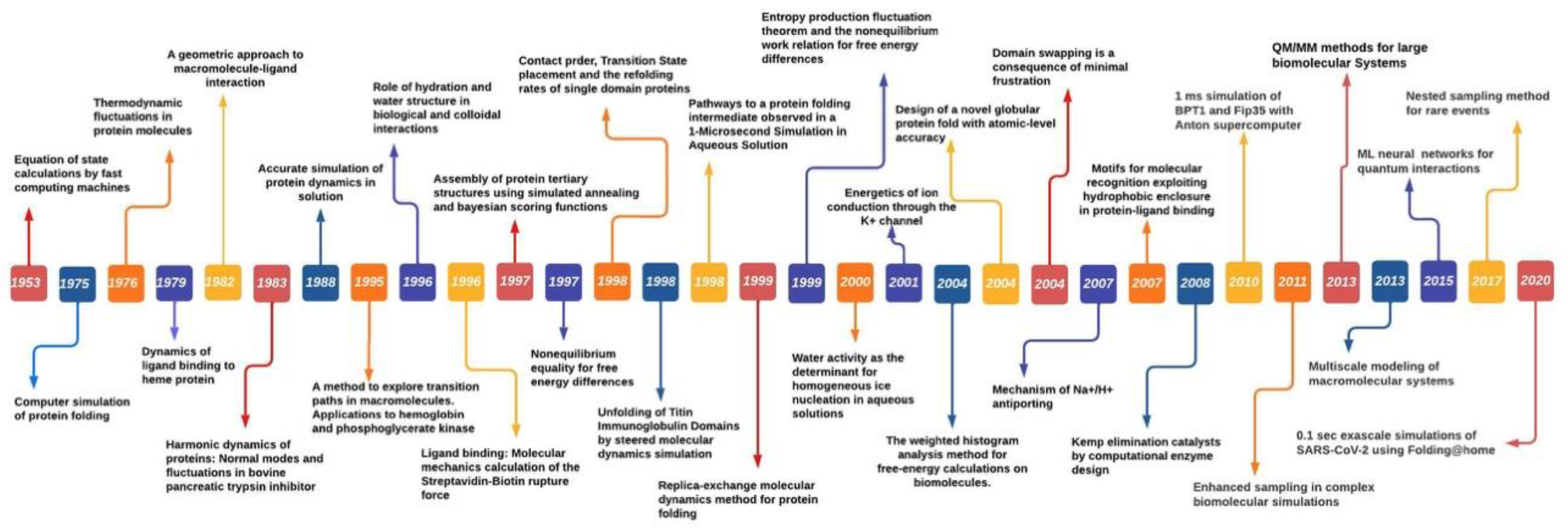
Figure 2.
The Molecular Simulations timeline showing the breakthrough achievements in MD Simulation studies.
3. Basic Concept of Force Field
Currently, it is a routine to simulate proteins with hundreds of amino acid residues at 10–100 ns surrounded by water and salt [30,31,32][30][31][32]. User-friendly platforms are widely available, i.e., GROMACS [33], AMBER [28], vCHARMM [34], DL_POLY [35], NAMD [26], LAMMPS [36] have been developed for MD Simulations analysis. The output of the platforms can be visualized and analyzed by external software, i.e., VMD [37], Chimera [38]. However, robust simulation requires appropriate parameters for studying a physical system. Force field, a set of mathematical expressions and parameters to describe the inter- and intra- molecular forces, are also essential to describe a physical system.
Three major molecular models have been developed: all-atom [39,40][39][40], coarse grained (CG) [41,42][41][42] and all-atom/coarse-grain mixed models [43,44,45][43][44][45] (Table 1). The all-atom force field for MD Simulation of lipid bilayers includes CHARMM, AMBER and OPLS-AA. GROMOS is an atomistic force field with an exception such as CHn modelled as united-atoms [46]. CHARMM (Chemistry at HARvard Macromolecular Mechanics) forcefield for lipids is widely used for simulating lipid bilayer and membrane proteins [47,48][47][48]. CHARMM force field is continuously updating and improving with the most recent version of CHARMM36m [49]. CHARMM36 lipid forcefield is parameterized for lipids [39], CHARMM36 DNA and CHARMM36 RNA are parameterized for DNA and RNA [50[50][51],51], CHARMM36m is parameterized for protein, and CHARMM General Force Field (CGenFF) is parameterized for drugs and general usage [52]. AMBER (Assisted Model Building with Energy Refinement) forcefield was developed in parallel. It treats all hydrogen atoms explicitly as CHARMM [53]. AMBER was designed and parameterized for specific biological systems: AMBER lipids 21 was parameterized for lipids [54]; AMBERff19SB was parameterized for proteins [55]; AMBER OL15 and AMBER OL3 were parameterized for DNA and RNA [56,57][56][57]; General AMBER forcefield (GAFF) was parameterized for drugs and general usage [58]; OPLS-AA (Optimized Parameters for Liquid Simulations All Atom) [59] was initially designed for simulating thermo-dynamical properties of short-chain hydrocarbons alkanes and later expanded to include lipids through a parameter set called OPLS/L [60], although the availability of lipids in the OPLS/L forcefield has not been as diverse as that of CHARMM and AMBER-compatible force fields. The latest improvement of OPLS-AA/M was its modification for peptides and protein torsional energetics [61]. The GROningen Molecular Simulation (GROMOS) forcefield utilizes a different approach for simulating analysis by fitting the parameters against experimental thermo-dynamic data. Its forcefield was generalized into a single package. The latest version is GROMOS 54A8 package updated in 2012 [62].
Table 1.
Atomistic and coarse-grained forcefield in MD Simulations.
| No. | Forcefield | Drugs | Lipid | DNA & RNA | Protein |
|---|---|---|---|---|---|
| 1 | GROMOS | GROMOS 43A1, GROMOS 45A3/4, GROMOS53A5/6, GROMOS54A7, GROMOS54B7, GROMOS54A8 | |||
| 2 | OPLS | OPLS-AA | OPLS-AA | OPLS-AA/M | OPLS-AA, OPLS-AA/L |
| 3 | CHARMM | CHARMM general force field (CGenFF) | CHARMM27 lipids, CHARMM36 lipids | CHARMM27 DNA, CHARMM27 RNA/DNA, CHARMM 36 RNA, CHARMM 36 DNA | CHARMM22/CMAP, CHARM27, CHARMM36, CHARMM36m |
| 4 | AMBER | General AMBER force field (GAFF) | LIPID14, LIPID21 | AMBER99 OL3, AMBER99bsc, AMBER OL15 | AMBER94, AMBER96, AMBER99, AMBER99sb, AMBER03, AMBER14sb, AMBER15ipq, AMBER19sb |
| 5 | MARTINI | MARTINI 2, MARTINI22, MARTINI22p, MARTINI 3, MARTINI dry, MARTINI ELNEDYN22, MARTINI ELNEDYNP22 | MARTINI 2, MARTINI22, MARTINI22p, MARTINI 3, MARTINI-Dry, MARTINI ELNEDYN22, MARTINI ELNEDYNP22 | MARTINI 2015 | MARTINI 2, MARTINI22, MARTINI22p, MARTINI 3, MARTINI dry, MARTINI ELNEDYN22, MARTINI ELNEDYNP22 |
| 6 | Coarse-grained forcefield models (additional) | - | Electrostatics-based model (ELBA) [90][63] protein-lipid CG model [91][64] |
PRIMONA, DMD, NAST, ENMs, oxRNA, SimRNA, SPQR | Rosetta centroid (CEN), UNRES, CABS, PRIMO, AWSEM, SURPASS, Scorpion, OPEP |
Compared to all-atom models, coarse-grained models significantly reduce the computing time by decreasing the number of particles explicitly during simulations. Over the last decade, coarse-grained model has also been widely used in protein [63][65] and nucleic acid studies [64,65][66][67]. Different coarse-grained models have been developed to extend the timescale of the simulation, since the first model used the concept of coarse grain in 1975 by Levitt and Warshal [66][68]. One of the most popular models is the MARTINI for membrane proteins [42], in which several atoms in protein and lipid are approximated as a single bead and four water molecules are treated as a single particle (known as one bead 4:1 mapping) although the beads can differ by their polarity or hydrophilicity. For particular cases, smaller beads can also be used, such as 3:1 and 2:1 mapping [67][69]. In MARTINI version 2.2, beads classified into 18 types are categorized into four groups: Q (charged), P (polar), N (intermediate) and C (apolar). In the latest version MARTINI 3, 29 beads have been sorted into seven groups with additional groups of halo-compounds (X), divalent ions (D) and water (W) [68][70]. MARTINI ELNEDIN model modified by utilizing an elastic network, with the peptide backbone beads position on the Cα atoms and heavier bead mass, improves the conformation transition in simulation [68][70]. MARTINI-Dry version provides an implicated solvation model [69][71]. The Born model is another model where the effects of the solvent and membrane are included implicitly in the simulation [70,71][72][73]. Implicit solvent forcefield is less used as it can cause significant errors due to it smoothen energy landscapes, which causes protein structure to deviate from the experimental crystal structure [72,73][74][75]. Coarse-grained protein models have been mainly used for analyzing protein folding mechanism and protein structure prediction [74,75][76][77]. Every alternate year, the CASP (Critical Assessment of Protein Structure Prediction) experiments provide an excellent platform to test the performance of coarse-grained models for predicting structures [76][78]. Several coarse-grained protein models apart from MARTINI are as follows: UNRES (united residue) [77][79], AWSEM (associated memory, water mediated, structure and energy model) [78][80], OPEP (optimized potential for efficient protein structure prediction) [79][81], SURPASS (Single United Residue per Pre-Averaged Secondary Structure fragment) [80][82] and CABS (C-alpha, c-beta, side chain) [81][83] models have been increasingly utilized for protein folding, structure prediction and interactions. PRIMO [82][84] and Scorpion [83][85] (solvated coarse-grained protein interaction) models are increasingly used in peptide and small protein structure prediction and protein–protein solvated complexes. The Rosetta centroid mode (CEN) model developed by Rohl et al. is also one of the widely used coarse-grained protein models in CASP protein structure prediction, de novo blind predictions, protein–protein and protein–ligand docking and modelling of protein-DNA interaction [84][86]. Coarse-grained models have been further utilized in nucleic acid molecular dynamics to analyze the three dimensional (3D) structural models of RNA [85,86,87][87][88][89]. Ding et al. introduced the discrete molecular dynamics (DMD) utilizing coarse-grained model to rapidly explore the conformational folding of RNA molecules [88][90]. Recently, Jonikas et al. have developed a fully automated coarse-grained model NAST (the nucleic acid simulation tool) using statistical potential capable enough to ensemble over 10,000 RNA plausible (3D) structures [89][91].
4. Molecular Simulations in Protein Study
The importance of MS arises from the fact that biomolecules such as proteins are under a dynamic state of motion, which is essential for the function of biomolecules. Although multiple experimental techniques can reveal the structural features of biomolecules, they are often incapable to show the dynamic features. MS provides a means to model the flexibility and conformational changes in the biomolecule at atomistic level, which is difficult to achieve by experimental approaches [11]. MS is more effective when combined with experiments to validate and improve the accuracy of experimental results. A key feature of MS is its ability to mimic both the in vitro and in vivo conditions, for example, at different pH conditions, in the presence of water and ions, at different salt or ionic concentrations, and in the presence of a lipid bilayer and other cellular components [92]. MS has been used to study multiple protein-related issues, such as protein-binding, protein–protein interaction and signaling [93]. The followings are examples.
References
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Mol. Biol. 2002, 9, 646–652.
- Minor, D.L., Jr. The neurobiologist’s guide to structural biology: A primer on why macromolecular structure matters and how to evaluate structural data. Neuron 2007, 54, 511–533.
- Coleman, J.A.; Green, E.M.; Gouaux, E. X-ray structures and mechanism of the human serotonin transporter. Nature 2016, 532, 334–339.
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 6.
- Alder, B.J.; Wainwright, T.E. Phase Transition for a Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209.
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341.
- Alder, B.J.; Wainwright, T.E. Studies in Molecular Dynamics. I. General Method. J. Chem. Phys. 1959, 31, 459–466.
- Rahman, A. Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev. 1964, 136, A405–A411.
- Rahman, A.; Stillinger, F.H. Molecular Dynamics Study of Liquid Water. J. Chem. Phys. 1971, 55, 3336–3359.
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249.
- McCammon, J.A.; Gelin, B.R.; Karplus, M. Dynamics of folded proteins. Nature 1977, 267, 585–590.
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341.
- Andersen, H.C. Molecular dynamics simulations at constant pressure and/or temperature. J. Chem. Phys. 1980, 72, 2384–2393.
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190.
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471–2474.
- Panagiotopoulos, A.Z. Direct determination of phase coexistence properties of fluids by Monte Carlo simulation in a new ensemble. Mol. Phys. 1987, 61, 813–826.
- Carter, E.A.; Ciccotti, G.; Hynes, J.T.; Kapral, R. Constrained reaction coordinate dynamics for the simulation of rare events. Chem. Phys. Lett. 1989, 156, 472–477.
- Voter, A.F. A method for accelerating the molecular dynamics simulation of infrequent events. J. Chem. Phys. 1997, 106, 4665–4677.
- Mills, G.; Jacobsen, W. Classical and Quantum Dynamics in Condensed Phase Simulations; World Scientific: Singapore, 1998.
- Weinan, E.; Ren, W.; Vanden-Eijnden, E. String method for the study of rare events. Phys. Rev. B 2002, 66, 052301.
- Ben-Nun, M.; Quenneville, J.; Martínez, T.J. Ab Initio Multiple Spawning: Photochemistry from First Principles Quantum Molecular Dynamics. J. Phys. Chem. A 2000, 104, 5161–5175.
- Jones, C.M.; List, N.H.; Martínez, T.J. Steric and Electronic Origins of Fluorescence in GFP and GFP-like Proteins. J. Am. Chem. Soc. 2022, 144, 12732–12746.
- Wasif Baig, M.; Pederzoli, M.; Kývala, M.; Cwiklik, L.; Pittner, J. Theoretical Investigation of the Effect of Alkylation and Bromination on Intersystem Crossing in BODIPY-Based Photosensitizers. J. Phys. Chem. B 2021, 125, 11617–11627.
- Meng, S.; Kaxiras, E. Real-time, local basis-set implementation of time-dependent density functional theory for excited state dynamics simulations. J. Chem. Phys. 2008, 129, 054110.
- Fitch, B.G.; Rayshubskiy, A.; Eleftheriou, M.; Ward, T.J.C.; Giampapa, M.; Zhestkov, Y.; Pitman, M.C.; Suits, F.; Grossfield, A.; Pitera, J.; et al. Blue Matter: Strong Scaling of Molecular Dynamics on Blue Gene/L. Comp. Sci. 2006, 3992, 846–854.
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802.
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447.
- Case, D.A.; Cheatham, T.E., 3rd; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688.
- Shaw, D.E.; Dror, R.O.; Salmon, J.K.; Grossman, J.P.; Mackenzie, K.M.; Bank, J.A.; Young, C.; Deneroff, M.M.; Batson, B.; Bowers, K.J.; et al. Millisecond-scale molecular dynamics simulations on Anton. In Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, Portland, OR, USA, 14–20 November 2009; p. 65.
- Levitt, M.; Sharon, R. Accurate simulation of protein dynamics in solution. Proc. Natl. Acad. Sci. USA 1988, 85, 7557–7561.
- Mackerell, A.D., Jr. Empirical force fields for biological macromolecules: Overview and issues. J. Comput. Chem. 2004, 25, 1584–1604.
- Price, D.J.; Brooks, C.L., 3rd. Modern protein force fields behave comparably in molecular dynamics simulations. J. Comput. Chem. 2002, 23, 1045–1057.
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718.
- Brooks, B.R.; Brooks, C.L., 3rd; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614.
- Smith, W.; Yong, C.W.; Rodger, P.M. DL_POLY: Application to molecular simulation. Mol. Simul. 2002, 28, 385–471.
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19.
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38.
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612.
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J. Phys. Chem. B 2010, 114, 7830–7843.
- Moore, P.B.; Lopez, C.F.; Klein, M.L. Dynamical properties of a hydrated lipid bilayer from a multinanosecond molecular dynamics simulation. Biophys. J. 2001, 81, 2484–2494.
- Saiz, L.; Klein, M.L. Computer simulation studies of model biological membranes. Acc. Chem. Res. 2002, 35, 482–489.
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824.
- Shi, Q.; Izvekov, S.; Voth, G.A. Mixed atomistic and coarse-grained molecular dynamics: Simulation of a membrane-bound ion channel. J. Phys. Chem. B 2006, 110, 15045–15048.
- Wan, C.-K.; Han, W.; Wu, Y.-D. Parameterization of PACE Force Field for Membrane Environment and Simulation of Helical Peptides and Helix–Helix Association. J. Chem. Theory Comput. 2012, 8, 300–313.
- Kar, P.; Gopal, S.M.; Cheng, Y.-M.; Panahi, A.; Feig, M. Transferring the PRIMO Coarse-Grained Force Field to the Membrane Environment: Simulations of Membrane Proteins and Helix–Helix Association. J. Chem. Theory Comput. 2014, 10, 3459–3472.
- Daura, X.; Mark, A.E.; Van Gunsteren, W.F. Parametrization of aliphatic CHn united atoms of GROMOS96 force field. J. Comput. Chem. 1998, 19, 535–547.
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, A.D. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273.
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616.
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73.
- Hart, K.; Foloppe, N.; Baker, C.M.; Denning, E.J.; Nilsson, L.; MacKerell, A.D. Optimization of the CHARMM Additive Force Field for DNA: Improved Treatment of the BI/BII Conformational Equilibrium. J. Chem. Theory Comput. 2012, 8, 348–362.
- Denning, E.J.; Priyakumar, U.D.; Nilsson, L.; Mackerell, A.D., Jr. Impact of 2′-hydroxyl sampling on the conformational properties of RNA: Update of the CHARMM all-atom additive force field for RNA. J. Comput. Chem. 2011, 32, 1929–1943.
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690.
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D., Jr. Extension of the CHARMM General Force Field to sulfonyl-containing compounds and its utility in biomolecular simulations. J. Comput. Chem. 2012, 33, 2451–2468.
- Dickson, C.J.; Walker, R.C.; Gould, I.R. Lipid21: Complex Lipid Membrane Simulations with AMBER. J. Chem. Theory Comput. 2022, 18, 1726–1736.
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552.
- Galindo-Murillo, R.; Robertson, J.C.; Zgarbová, M.; Šponer, J.; Otyepka, M.; Jurečka, P.; Cheatham, T.E. Assessing the Current State of Amber Force Field Modifications for DNA. J. Chem. Theory Comput. 2016, 12, 4114–4127.
- Zgarbová, M.; Otyepka, M.; Šponer, J.; Mládek, A.; Banáš, P.; Cheatham, T.E.; Jurečka, P. Refinement of the Cornell et al. Nucleic Acids Force Field Based on Reference Quantum Chemical Calculations of Glycosidic Torsion Profiles. J. Chem. Theory Comput. 2011, 7, 2886–2902.
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174.
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236.
- Komáromi, I.; Owen, M.C.; Murphy, R.F.; Lovas, S. Development of glycyl radical parameters for the OPLS-AA/L force field. J. Comput. Chem. 2008, 29, 1999–2009.
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509.
- Reif, M.M.; Hünenberger, P.H.; Oostenbrink, C. New Interaction Parameters for Charged Amino Acid Side Chains in the GROMOS Force Field. J. Chem. Theory Comput. 2012, 8, 3705–3723.
- Orsi, M.; Essex, J.W. The ELBA Force Field for Coarse-Grain Modeling of Lipid Membranes. PLoS ONE 2011, 6, e28637.
- Shih, A.Y.; Arkhipov, A.; Freddolino, P.L.; Schulten, K. Coarse grained protein-lipid model with application to lipoprotein particles. J. Phys. Chem. B 2006, 110, 3674–3684.
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936.
- Uusitalo, J.J.; Ingólfsson, H.I.; Akhshi, P.; Tieleman, D.P.; Marrink, S.J. Martini Coarse-Grained Force Field: Extension to DNA. J. Chem. Theory Comput. 2015, 11, 3932–3945.
- Šulc, P.; Romano, F.; Ouldridge, T.E.; Doye, J.P.; Louis, A.A. A nucleotide-level coarse-grained model of RNA. J. Chem. Phys. 2014, 140, 235102.
- Levitt, M.; Warshel, A. Computer simulation of protein folding. Nature 1975, 253, 694–698.
- De Jong, D.H.; Singh, G.; Bennett, W.F.D.; Arnarez, C.; Wassenaar, T.A.; Schäfer, L.V.; Periole, X.; Tieleman, D.P.; Marrink, S.J. Improved Parameters for the Martini Coarse-Grained Protein Force Field. J. Chem. Theory Comput. 2013, 9, 687–697.
- Periole, X.; Cavalli, M.; Marrink, S.-J.; Ceruso, M.A. Combining an Elastic Network With a Coarse-Grained Molecular Force Field: Structure, Dynamics, and Intermolecular Recognition. J. Chem. Theory Comput. 2009, 5, 2531–2543.
- Arnarez, C.; Uusitalo, J.J.; Masman, M.F.; Ingólfsson, H.I.; de Jong, D.H.; Melo, M.N.; Periole, X.; de Vries, A.H.; Marrink, S.J. Dry Martini, a Coarse-Grained Force Field for Lipid Membrane Simulations with Implicit Solvent. J. Chem. Theory Comput. 2015, 11, 260–275.
- Bashford, D.; Case, D.A. Generalized born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 2000, 51, 129–152.
- Im, W.; Chen, J.; Brooks, C.L. Peptide and Protein Folding and Conformational Equilibria: Theoretical Treatment of Electrostatics and Hydrogen Bonding with Implicit Solvent Models. In Advances in Protein Chemistry; Academic Press: Cambridge, MA, USA, 2005; Volume 72, pp. 173–198.
- Zhang, J.; Zhang, H.; Wu, T.; Wang, Q.; van der Spoel, D. Comparison of Implicit and Explicit Solvent Models for the Calculation of Solvation Free Energy in Organic Solvents. J. Chem. Theory Comput. 2017, 13, 1034–1043.
- Zhou, R. Free energy landscape of protein folding in water: Explicit vs. implicit solvent. Proteins Struct. Funct. Bioinform. 2003, 53, 148–161.
- Chouard, T. Structural biology: Breaking the protein rules. Nature 2011, 471, 151–153.
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972.
- Moult, J.; Fidelis, K.; Kryshtafovych, A.; Schwede, T.; Tramontano, A. Critical assessment of methods of protein structure prediction (CASP)--round x. Proteins 2014, 82 (Suppl. S2), 1–6.
- Liwo, A.; Baranowski, M.; Czaplewski, C.; Gołaś, E.; He, Y.; Jagieła, D.; Krupa, P.; Maciejczyk, M.; Makowski, M.; Mozolewska, M.A.; et al. A unified coarse-grained model of biological macromolecules based on mean-field multipole-multipole interactions. J. Mol. Modeling 2014, 20, 2306.
- Davtyan, A.; Schafer, N.P.; Zheng, W.; Clementi, C.; Wolynes, P.G.; Papoian, G.A. AWSEM-MD: Protein Structure Prediction Using Coarse-Grained Physical Potentials and Bioinformatically Based Local Structure Biasing. J. Phys. Chem. B 2012, 116, 8494–8503.
- Sterpone, F.; Melchionna, S.; Tuffery, P.; Pasquali, S.; Mousseau, N.; Cragnolini, T.; Chebaro, Y.; St-Pierre, J.-F.; Kalimeri, M.; Barducci, A.; et al. The OPEP protein model: From single molecules, amyloid formation, crowding and hydrodynamics to DNA/RNA systems. Chem. Soc. Rev. 2014, 43, 4871–4893.
- Dawid, A.E.; Gront, D.; Kolinski, A. SURPASS Low-Resolution Coarse-Grained Protein Modeling. J. Chem. Theory Comput. 2017, 13, 5766–5779.
- Kolinski, A. Protein modeling and structure prediction with a reduced representation. Acta Biochim. Pol. 2004, 51, 349–371.
- Kar, P.; Gopal, S.M.; Cheng, Y.-M.; Predeus, A.; Feig, M. PRIMO: A Transferable Coarse-Grained Force Field for Proteins. J. Chem. Theory Comput. 2013, 9, 3769–3788.
- Basdevant, N.; Borgis, D.; Ha-Duong, T. Modeling Protein–Protein Recognition in Solution Using the Coarse-Grained Force Field SCORPION. J. Chem. Theory Comput. 2013, 9, 803–813.
- Rohl, C.A.; Strauss, C.E.; Misura, K.M.; Baker, D. Protein structure prediction using Rosetta. Methods Enzym. 2004, 383, 66–93.
- Cao, S.; Chen, S.J. Predicting structures and stabilities for H-type pseudoknots with interhelix loops. RNA 2009, 15, 696–706.
- Setny, P.; Zacharias, M. Elastic Network Models of Nucleic Acids Flexibility. J. Chem. Theory Comput. 2013, 9, 5460–5470.
- Boniecki, M.J.; Lach, G.; Dawson, W.K.; Tomala, K.; Lukasz, P.; Soltysinski, T.; Rother, K.M.; Bujnicki, J.M. SimRNA: A coarse-grained method for RNA folding simulations and 3D structure prediction. Nucleic Acids Res. 2016, 44, e63.
- Ding, F.; Sharma, S.; Chalasani, P.; Demidov, V.V.; Broude, N.E.; Dokholyan, N.V. Ab initio RNA folding by discrete molecular dynamics: From structure prediction to folding mechanisms. RNA 2008, 14, 1164–1173.
- Jonikas, M.A.; Radmer, R.J.; Laederach, A.; Das, R.; Pearlman, S.; Herschlag, D.; Altman, R.B. Coarse-grained modeling of large RNA molecules with knowledge-based potentials and structural filters. RNA 2009, 15, 189–199.
- Van Gunsteren, W.F.; Berendsen, H.J.C. Computer Simulation of Molecular Dynamics: Methodology, Applications, and Perspectives in Chemistry. Angew. Chem. Int. Ed. Engl. 1990, 29, 992–1023.
- Dror, R.O.; Dirks, R.M.; Grossman, J.P.; Xu, H.; Shaw, D.E. Biomolecular simulation: A computational microscope for molecular biology. Annu. Rev. Biophys. 2012, 41, 429–452.
More
