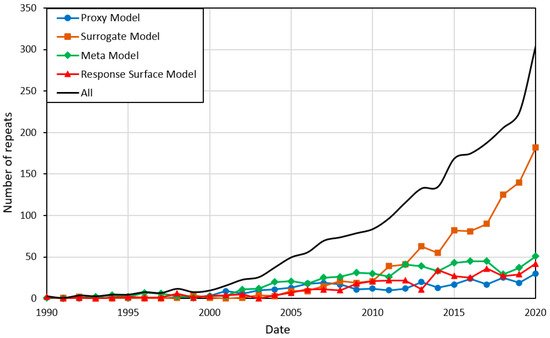
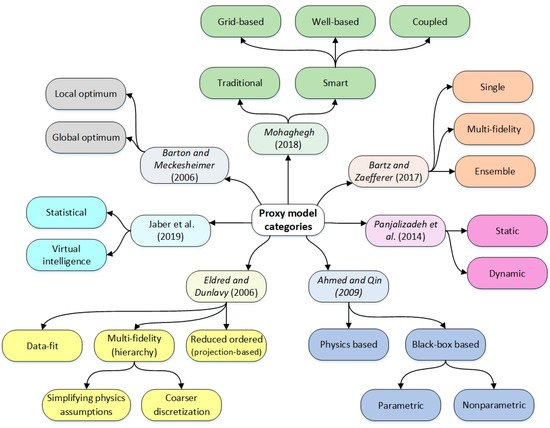
3.2. Reduced-Order Models (ROM)
4.2. Reduced-Order Models (ROM)
The popular methods in the class of ROM that are used for reservoir modeling approximations are POD, TPWL, and DEIM. As discussed in
Section 2, ROM methods project the exact model into a lower-dimensional subspace. The subspace basis in POD is achieved by accomplishing a singular value decomposition of a matrix containing the solution states obtained from previous runs
[34][144]. POD has been implemented in different areas such as reservoir modeling
[35][36][145,146], finding the optimal control parameters in water flooding
[37][38][147,148], and history matching
[39][149]. Nevertheless, POD methods need to solve the full Jacobean of the matrix for projecting the non-linear terms in every iteration. Since the reservoir environment is highly non-linear, the speedup potential of POD to approximate the reservoir simulation is not significant. For instance, Cardoso et al.
[36][146] achieved speedups of at most a factor of 10 for ROMs based on POD in reservoir simulation. To solve this drawback, retain the non-linear feature of parameters and further increase the speedup potential, a combination of the TPWL or DEIM method and POD has been the focus of attention in the literature. The combination of TPWL and POD was implanted in various cases such as waterflooding optimization
[40][41][150,151], history matching
[42][43][152,153], thermal recovery process
[44][154], reservoir simulation
[40][150], and compositional simulation
[45][155]. In work carried out by Cardoso and Durlofsky
[40][150], a POD in combination with TPWL could increase the speedup for the same reservoir discussed earlier from a factor of 10 to 450. Additionally, the application of DEIM and POD is applied in some studies to create proxies for reservoir simulation
[46][47][156,157], fluid flow in porous media
[48][49][158,159], and water flooding optimization
[50][160].
3.3. Traditional Proxy Models (TPM)
4.3. Traditional Proxy Models (TPM)
In the literature, a wide variety of techniques can be considered as TPMs. This type of proxy can approximate different areas in the subsurface or surface environment such as production optimization
[51][52][100,167], uncertainty quantification
[53][54][168,169], history matching
[55][56][170,171], field development planning
[57][172], risk analysis
[58][59][173,174], gas lift optimization
[60][61][109,175], gas storage management
[62][176], screening purposes in fractured reservoirs
[63][177], hydraulic fracturing
[64][178], assessing the petrophysical and geomechanical properties of shale reservoirs
[65][179], waterflooding optimization
[66][67][68][69][180,181,182,183], well placement optimization
[70][71][72][184,185,186], wellhead data interpretation
[73][187], and well control optimization
[74][188]. Additionally, TPMs have a wide range of applications in various EOR recovery techniques such as steam-assisted gravity drainage (SAGD)
[75][189], CO
2-gas-assisted gravity drainage (GAGD)
[76][190], water alternating gas (WAG)
[77][78][191,192], and chemical flooding
[79][193].
3.4. Smart Proxy Models (SPM)
4.4. Smart Proxy Models (SPM)
SPMs are implemented in various areas such as waterflood monitoring
[80][81][20,194], gas injection monitoring
[82][21], and WAG monitoring
[83][18] using the grid-based SPM, history matching
[84][85][19,22], and production optimization in a WAG process
[83][18] using the well-based SPM.
45. Conclusions
The most significant advantage of constructing a proxy model is the reduction in computational load and the time required for tasks such as uncertainty quantification, history matching, or production forecasting and optimization. According to the literature, different classes of proxy models exist, and there is no agreement on the proxy model categorization. Existing categories do not provide a comprehensive overview of all proxy model types with their applications in the oil and gas industry. Furthermore, a guideline to discuss the required steps to construct proxy models is needed. The proxy models
in this work can fall into four groups: multi-fidelity, reduced-order, traditional proxy, and smart proxy models. The methodology for developing the multi-fidelity models is based on simplifying physics, and reduced-order models are based on the projection into a lower-dimensional. The procedure to develop traditional and smart proxy models is mostly similar, with some additional steps required for smart proxy models. Smart proxy models implement the feature engineering technique, which can help the model to find new hidden patterns within the parameters. As a result, smart proxy models generate more accurate results compared to traditional proxy models. Different steps for proxy modeling construction are comprehensively discussed
in this review. For the first step, the objective of constructing a proxy model should be defined. Based on the objective, the related parameters are chosen, and sampling is performed. The sampling can be either stationary or sequential. Then, a new model is constructed between the considered inputs and outputs. This underlying model may be trained based on statistics, machine learning algorithms, simplifying physics, or dimensional reduction.