The concept of heat transfer refers to the flow of thermal energy through a process that involves a difference in temperature, subsequently leading to changes and redistribution of temperature. The study of transport phenomena involves the exchange of mass, momentum, and energy in the form of radiation, convection, and conduction. HT enhancement is a technique that can be utilized to improve the rate of heat removal. These techniques are further divided into two clusters: active and passive, as shown in Figure 1. Active enhancement techniques include ultrasonic enhancement and electrohydrodynamic, whereas the use of passive enhancement techniques can add extended surfaces, enhance thermal conductivity, and make surface or geometrical modifications to the flow channel by using inserts or additional devices, as shown in Figure 1. Boiling, unlike pure conduction, is a phase-changing process of convection and radiation that involves a high rate of heat transfer from a liquid to a vapour state. When a surface is exposed to liquid, and its saturation temperature exceeds that of the liquid, it becomes hot enough to cause boiling. This can be understood by the boiling curve. Boiling has many industrial applications, such as in steam production, distillation, refining, dehydration, cooling of nuclear reactors, metallurgical processing, air conditioning, refrigeration and cryogenics, fluid handling and control, power systems, electronics cooling, on-orbit storage, microchip cooling, chemical process industries, space systems, thermal management, food processing, health care processes, etc. The heat transfer rate/heat flux in boiling is calculated by using:

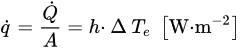
where h = HT Coefficient (W/(m²∙K), A = Area (m²), ∆T_e = Excess Temperature = T_surface−T_saturation, T_S = Surface Temperature, and T_sat = Saturation Temperature of Liquid.

2. Surface Characteristics

Surface roughness and porosity are parameters that must be considered when enhancing the heat transfer rate. Both parameters are described below:

• Roughness was found to have a large effect on the heat transfer rate in one of the early research works by Jerome, 1960 [2]. With an increased roughness in a particular metal of particular geometry, there were greater occurrences of active nucleation sites. Having a higher density of sites may enhance the heat transfer coefficient.
• Porosity also enhances the heat transfer rate. Surface porosity can be increased by manually/artificially creating cavities on the surface.

• Roughness was found to have a large effect on the heat transfer rate in one of the early research works by Jerome, 1960 ^[1]. With an increased roughness in a particular metal of particular geometry, there were greater occurrences of active nucleation sites. Having a higher density of sites may enhance the heat transfer coefficient.
• Porosity also enhances the heat transfer rate. Surface porosity can be increased by manually/artificially creating cavities on the surface.

Utilizing the above-mentioned surface modifications and a cylindrical surface as the geometric modification, this experiment aimed to increase the rate of heat transfer, and investigate how these passive heat transfer enhancement techniques affected the heat transfer rate. 

3. Background of Boiling Heat Transfer

Nukiyama, 1934 [3]^[2] ran the very first study on boiling heat transfer in Japan. He experimented with saturated pool boiling around an electrically heated platinum wire. The boiling regimes sho wn in Figure 2 was partially discovered by Nukiyama. He plotted nucleate boiling and film boiling on a q. T  plot but was unable to explain the process between nucleate and film boiling, which is now known as transition boiling. The studies of Nukiyama were later validated by Drew and Mueller, 1937 [4]^[3] through experiments performed on an organic liquid. Since then, there have been numerous studies performed on various subtopics related to nucleate and film boiling, and boiling heat transfer. Guo et al., 1998 [5]^[4] proposed a new approach to the convective heat transfer energy equation. They noted that enhancement of the synergetic effect between velocity and temperature could be increased by raising mean heat convection intensity and the dimensionless temperature difference. This could be achieved using a combination of methods. According to the field synergy principle, increasing the synergy between the velocity and heat flow fields may result in an increase of heat transfer. This is useful in various engineering fields as it can reduce flow resistance and improve the efficiency of a system. The synergistic interaction between the velocity vector and the temperature gradient is quantified by the field synergy angle. Thus, heat transfer augmentation could be accomplished using this approach. Then, the authors introduced heat convection velocity. The first step in this process was to explore the mechanism by which heat convection velocity could be generated in a smooth circular tube. The heat transfer in the circular tube was then improved by creating a new insert. An analysis of heat convection velocity was carried out to study various aspects of the enhanced tube.

4. Techniques to Improve Heat Exchange

Heat transfer enhancement is the process of increasing the heat transfer rate (or improving performance, to be more precise). There have been numerous studies on the methods of enhancing heat transfer. Bergles, 1997 [6]^[5] categorized both active and passive techniques used in improving heat transmission. Figure 1 illustrates the classification of heat transfer enhancement techniques, with examples. Calmidi and Mahajan, 2000 [7]^[6] performed an experimental and numerical study on aluminum metal foams with high porosity for single-phase forced convection. They found good agreement between the numerical results and their experimental findings. Mori and Okuyama, 2009 [8]^[7] investigated pool boiling using a honeycomb porous media. The critical heat flux (CHF) increased approximately 2.5 times more than on a plain surface. They also calculated CHF performance with capillary suction, permeability, pore radius, wall thickness, height of the porous media, and vapour scope channels. Al-Zaidi et al., 2019 [18]^[8], investigated the impact of the channel aspect ratio on HFE-7100 flow boiling properties, including flow patterns, heat transmission, and pressure drop in copper multi-microchannel heat sinks. The average surface roughness of the channel bottom surface was nearly the same in the three heat sinks, with a base area of 500 mm² and channel hydraulic diameter of 0.46 mm. The HFE-7100 flow boiling experiments were carried out in horizontal multi-microchannel heat sinks. The flow patterns that were observed included bubbly, slug, churn, and annular flow. There were also small nucleating bubbles visible in the annular flow liquid film. Forward motion, stagnation period, and backward motion were discovered to represent the flow reversal cycle. As a result of this flow reversal, pressure drop fluctuated more in channels with small aspect ratios. The heat transfer coefficient was larger when vapor quality was low, but decreased as vapour quality rose. The amount of heat that could be removed from the chipset (base heat flow) increased with a reduced channel aspect ratio. Further study of other aspect ratio ranges, operational conditions, and working fluids is required to validate these findings.

5. Heat Transfer Enhancement in Heat Exchangers

There have been numerous studies in the field of heat exchangers on how to improve the ability to transfer heat by using different types of inserts and tube geometries. Abdel-Rahmen et al., 1996 [36]^[9] demonstrated that the perfect tape width exists, and to see the best thermohydraulic performance, researchers need to pay attention to the Reynolds number and twist ratio. Freund et al., 2004 [37]^[10] also studied hydraulic and thermal performance when tape was inserted in a large, hydraulic diameter annulus in the shape of a twist. This research has led to other similar research. Promvonge et al., 2007 [38]^[11] studied circular tubes with twisted tapes and saw that the heat transferability of a conventional heat exchanger increases when twisted tapes are introduced. Nanan et al., 2014 [39]^[12] examined the effect on heat transfer when helical screw tape was used, in a double pipe, both with and without a core rod; they concluded that helical screw tape used without the core rod gave better results than with the core rod. Thianpong et al., 2012 [40]^[13] tested the heat transfer coefficient and friction factor values for various twisted and wing cut ratio values. Thianpong et al., 2012 [41]^[14] also studied twisted cassettes with alternating counterclockwise and clockwise directions, from which clockwise twisted tapes were found to be better at heat transfer. Wongcharee et al., 2011 [42]^[15] compared twisted tapes with alternating wings along the axis as inserts and found that alternating wings were better at heat transfer. Another study by Eiamsa-Ard et al., 2010 [43]^[16] found that temperature-transfer efficiency and the friction factor value was maximized when the twist ratio for alternate twisted tapes in clockwise and counterclockwise directions was set to three. Eiamsa-Ard et al., 2010 [44]^[17] further validated that a tube with a twist ratio of three is better at heat transfer. Eiamsa-Ard et al., 2009 [45]^[18] observed the greatest rate of heat transmission in the tube when it was connected with a conical ring and twisted tape, compared with smooth tubes. Thianpong et al., 2012 [41]^[14] experimented with twisted tapes and ring turbulators in a circle with varying ratios of pitch and twist. A combination of a circular ring and tapes showed maximum thermal performance compared with a pitch ratio and twist ratio of one and three, respectively. Eiamsa-Ard et al., 2009 [45]^[18] studied consistent and irregular twisted tapes with alternative axes for Reynolds numbers ranging from 5K to 21.5K. They concluded that a tube using twisted tapes with alternate axes that are non-uniform and has the smallest value of alternate length to twist length ratio is better at heat transfer. Eiamsa-Ard et al., 2010 [43]^[16] also studied the effects of serrated-edge twisted tapes on the performance of heat exchangers and concluded that increasing the width ratio and decreasing the depth ratio enhances performance. Promvonge et al., 2012 [46]^[19] found that a dimpled tube with inserted twisted tape had a high friction factor, more convective heat transfer, and overall, more efficient convective heat transfer than a smooth dimpled tube. Skullong et al., 2016 [47]^[20] used twisted tape with perforations and parallel wings to improve heat transfer in a circular tube. Wings produced obstacles and perforations reduced the friction factor by releasing the flow. They concluded that thermal performance is maximized when the hole diameter ratio is minimized and wing depth ratio is maximized. Pethkoolet al., 2010 [48]^[21] compared helically corrugated tubes and smooth tubes and concluded that helically corrugated tubes are better at heat transfer and have higher values of the heat transfer coefficient when compared with a smooth tube. Nanan et al., 2014 [39]^[12] studied perforated helical twisted-tape inserts, keeping the twist ratio constant and varying the ratios between the diameter and perforation pitches. They found that when the perforation diameter decreases and perforation pitch increases, thermal performance factor also increases. Using twisted tape with perforation decreased the intensity of turbulence and area of blockage, resulting in reduced friction and a reduced heat transfer rate, unlike when inserted with a solid insert. Kongkaitpaiboon et al., 2010 [49]^[22] also studied solid and perforated conical rings and found that reducing the pitch ratio and number of perforated holes increased the heat transfer rate and friction factor of perforated conical rings; however, the thermal performance factor rose when the pitch ratio and number of perforated holes were reduced. Guo et al., 2011 [50]^[23] tested center-cleared twisted tape used as inserts in a circular tube, and found improved thermohydraulic performance. By cutting the edges of twisted tapes to a narrow width, thermohydraulic performance was degraded. Chang et al., 2007 [51]^[24] compared tapes with a different number of twists, ranging from one to three, and concluded that triple twisted tapes showed the highest performance factors for turbulence. Kathait and Patil, 2014 [52]^[25] studied the heat transfer and frictional losses in a heat exchanger tube as a function of discrete corrugated rib roughness and found that a corrugated tube with five gaps improved the Nusselt number and friction factor. Vashistha et al., 2016 [53]^[26] reported in a review that studies using twisted tapes with a twist ratio of 2.5 significantly increased heat transfer, with a comparable increase in friction losses, compared with a smooth tube. The highest heat transfer rate and friction enhancements were determined to be 2.42 and 6.96 times that of a smooth tube, respectively. Li et al., 1982, [54]^[27] using high speed and flow visualization, explained the flow structure of helically finned tubes. They employed one to three fin beginnings, four tubes with rounded ribs, and helix angles between 38 and 80° in their investigation. It was observed from photographs that there were parabolic patterns of bubbles in laminar flow. These patterns break in turbulent flow, due to random separation vortices. Li et al., 1982 [54]^[27] found that both spiral pattern and boundary-layer separation flow occurred in helical ridging tubes; however, they occurred with different intensities in the tubes, having different configurations. Wen et al., 2004 [55]^[28] showed that maximum enhancement occurs at an axial distance of approximately a hundred times more than the tube diameter.

6. Nanofluids

In recent years, energy consumption has exponentially increased for things such as electronic devices, nuclear power reactors, the cooling of rocket nozzles, etc. Thermal management is classified into single-phase and two-phase heat transfer. Two-phase heat transfer has higher heat transfer efficiency compared with single-phase heat transfer; however, this process is very complicated, and involves bubble formation, condensation, vapour quality, flow boiling geometry, liquid subcooling temperature, etc. Therefore, new technologies such as making surface modifications, decreasing flow area dimensions, using nanofluids and porous media structures, etc., have been proposed by researchers to increase the heat flux and CHF. In a variety of heat transfer applications, including heat exchangers, cooling of electronic equipment, and chemical processes, nanofluids are considered the heat transfer fluid of the future. Small solid particles suspended in energy transmission fluids can increase thermal conductivity, which is an efficient and creative technique to greatly improve heat transfer properties. Numerous researchers have rim experimental and numerical studies to investigate the use of nanofluids to manage heat transfer, due to their expanding use in applications in recent years. Nanofluids have been shown to improve critical heat flux under pool boiling conditions due to deposits of the nanoparticle on the heater surface (Kim et al., 2007 [56]^[29]). The use of nanofluid in buildings was investigated by Amirahmad et al., 2021 [57]^[30]. Gunnasegaran et al., 2012 [58]^[31] studied numerical simulations of nanofluid flow. They discussed two types of compact heat exchangers (CHE): thermal and hydraulic. Thermal and hydraulic CHEs were studied using conventional coolant to determine how nanofluids affect factors such as heat transfer coefficient variation, shear stress skin friction, pressure drop, and pumping power as a function of the Reynolds number. Maddah et al., 2014 [59]^[32] studied heat transfer in a double-pipe heat exchanger fitted with twisted-tape elements and titanium dioxide nanofluid. Maddah et al., 2018 [60]^[33] explored the increase in heat transfer in a twin-pipe heat exchanger using a nanofluid combining water and aluminium oxide nanoparticles in turbulent flow. The heat transfer values were determined in the nanofluid turbulent flow, containing 20 nm aluminium oxide suspended particles in water at a volume concentration of 0.1–0.3%. According to a comparison based on a fixed Reynolds number, the heat transfer coefficient and Nusselt number of the nanofluid increased by 15 to 20% compared with the base fluid. The addition of nanoparticles to the fluid increased the average heat transfer coefficient in the turbulent flow regime. The Reynolds number increased together with the overall heat transfer coefficient. Two potential causes of this increase were the use of a nanofluid with suspended nanoparticles that could have enhanced the thermal conductivity of the mixture, or a high energy exchange process that was brought on by the amorphous mobility of the nanoparticles. Sandeep et al., 2016 [17]^[34], in their review paper, observed that nanoparticles pose less of a risk for heat exchanger problems, such as abrasion, clogging, fouling, and additional pressure loss, than bigger particles. This is due to their similar size to the molecules of the base fluids and higher thermal conductivity than the working fluids. The inclusion of nanoparticles helps in the construction of more efficient heat exchange equipment, as they improve thermal conductivity of regular cooling fluids, such as water, oil, and ethylene-glycol. A theoretical inquiry investigated how nanoparticle migration affects the improvement of heat transmission during film boiling of nanofluids across a vertical cylinder. Two different kinds of nanoparticles, titania and alumina, were taken into consideration. Their effectiveness in accelerating the rate of heat transfer was investigated. Nanoparticles that are not evenly dispersed throughout the film can gather at the heated wall due to thermophoresis. This results in increased heat transmission rates. The net improvement or decrement in the heat transfer rate, however, depends on the trade-off between a decrease in thermal conductivity and an increase in the temperature gradient at the wall. In order to improve this performance, Freitas et al., 2021 [61]^[35] investigated combining personalised surface modifications with the usage of nanofluids.

7. Effect of Droplet Dynamics on Heat Transfer

During droplet spreading and receding phases below the saturation temperature, droplet temperature changes spatially and temporally, making it difficult to measure. Pasandideh-Fard et al., 2002 [62]^[36] studied the effect of droplet diameter on heat transfer characteristics when a droplet falls onto a flat or smooth surface, and developed a mathematical model for this process. Larsen et al., 2011 [63]^[37] conducted numerical simulations and presented a modified equation of cooling effectiveness for smooth surfaces. Roisman, 2009 [64]^[38] with the help of the N–S equation and energy transport equation, examined the flow and heat transfer characteristics of impinging droplets with consideration of phase change. Herbert et al., 2013, [65]^[39] with the help of dimensionless numbers, also studied heat transfer during droplet impact. Another study by Ahn et al., 2012 [66]^[40] looked at the behavior of an impinging droplet on a heated textured surface, and examined the variation in the evaporating meniscus by measuring the dynamic contact angle. There have been several other studies by Alizadeh et al., 2012, Negeed et al., 2014, Tran et al., 2012 [67,68,69]^[41][42][43] on spreading and receding dynamics, the effect of surface smoothness, phase change of droplet impacts on heated rough surfaces, and the Leidenfrost phenomena of a droplet on a textured surface; however, there is a deficiency of experimental data. A study by Moon et al., 2016 [70]^[44] suggested a modified equation for total thermal energy and studied the cooling effectiveness for the three types of wetting surfaces, i.e., partial, non-wetting, and total wetting. Due to the holes of the textured surface, a liquid droplet spreads and penetrates the surface, leading to the formation of the air pockets. When this phenomenon occurred on a heated surface, it resulted in the recoil of diameter, although initially the contact diameter increased. This was because the viscosity of the thin layer of liquid decreased on the heated surface.