Introduction

Tautomerism is typically the relocation of a light atom, often hydrogen, at the same time as a rearrangement of the electronic structure.  Typical examples are acetylacetone and acetone.  In the latter molecule a keto-enol equilibrium is present (Figure 1), but the enol form is in a very low amount and not “visible”.

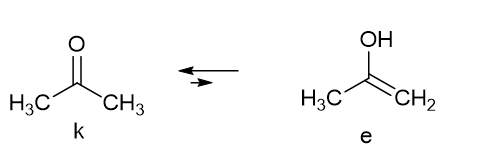
Figure 1.  Acetone tautomeric equilibrium.

In the case of acetylacetone (as a representative of the broader group of β-diketones) two equilibria takes place, a keto-enol one, which is slow at the NMR time scale (which means that separate resonances from the two tautomers can be observed)  and a fast movement of the enol proton from one oxygen to the other

(Figure 2). 

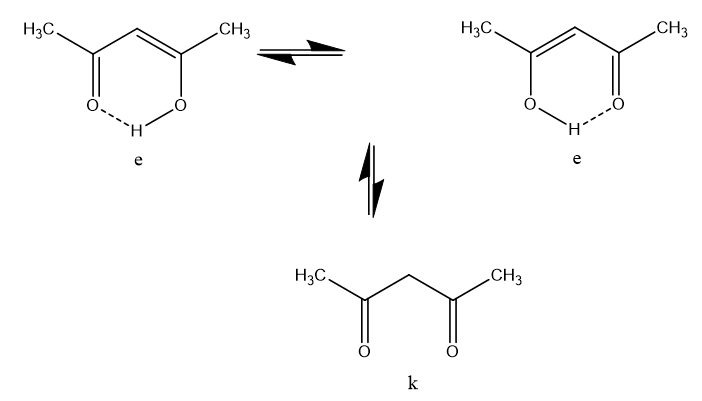
Figure 2.  Tautomeric species of acetylacetone.

This latter equilibrium is very fast (the barrier is very low).  It is not visible as such, but can be inferred from the fact that the two methyl resonances have the same chemical shift (see Figure 3). However, this is not the case in unsymmetrical cases.  It is already clear that it can be difficult to detect the presence of an equilibrium.  Could other spectroscopic techniques be useful?  Yes, Infra Red spectroscopy is usually fast enough to detect the two tautomers and so is UV-VIS spectroscopy.  However, Infra Red spectra of tautomeric compounds with two or more forms become very complex to interpret and for UV-VIS both forms may not have suitable chromophores.  NMR clearly suffers from being a “slow” technique and will typically only provide average chemical shifts and coupling constants.

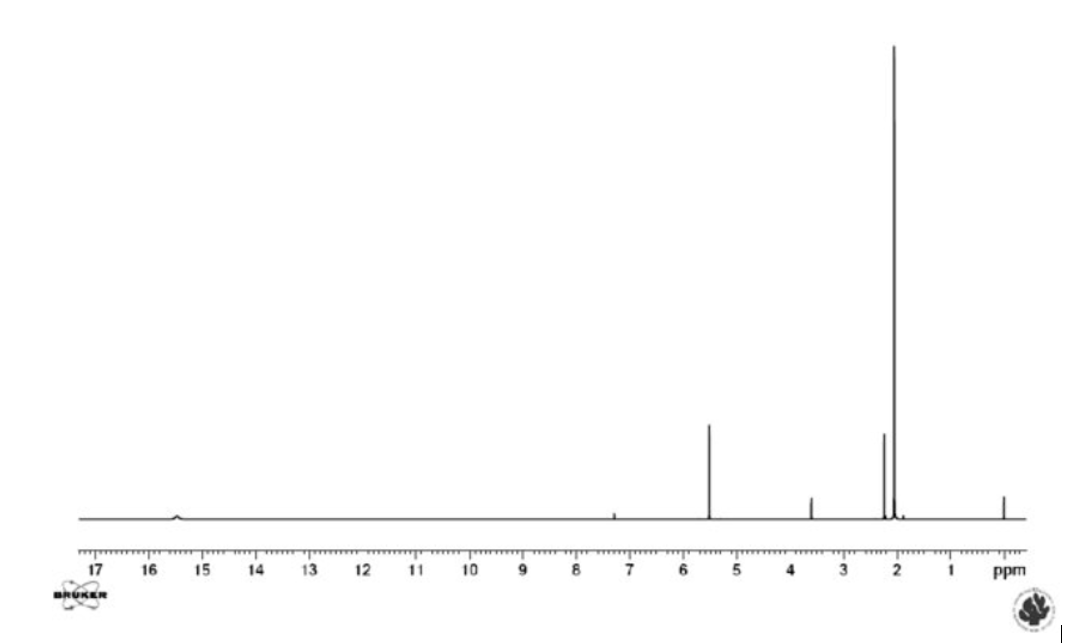
Figure 3.  ¹H NMR spectrum of acetylacetone in CDCl₃.  The resonances belonging to the keto form are those at 3.6 and 2.2 ppm.

Using NMR we are concentrating on chemical shifts, coupling constants and isotope effects on chemical shifts and temperature can be of additional help.  Furthermore, as we often only observe an average signal, it is very useful to know the parameters of both tautomers.  Density Functional Theory (DFT) calculations may be of great help.  It is important that tautomeric equilibria can occur both in solution and in the solid state. ^[1]

Chemical shifts primarily used in tautomeric studies are ¹H, ¹³C, ¹⁵N and ¹⁹F (if present) and to a much lesser degree ¹⁷O.  Common for the latter four nuclei is a very large chemical shift range.

¹H and ¹³C chemical shifts

 ¹H is especially interesting when looking at XH protons (X=O, N or S) and when a large chemical shift difference is present between the two tautomers.  A case is β-thioxoketones in which a large chemical shift difference is found between OH and SH chemical shifts, as well as large chemical shift differences between ¹³C chemical shifts of C=S and CSH exist (see Table 1).  Furthermore, large equilibrium isotope effects are also seen in this type of tautomeric equilibrium (see later).  However, one may easily make mistakes as in the present case by only assuming the traditional two types of tautomers (A and B of Figure 4).  It turns out that also an open form with the SH not hydrogen bonded does exist (form C of Figure 4). ^[2]

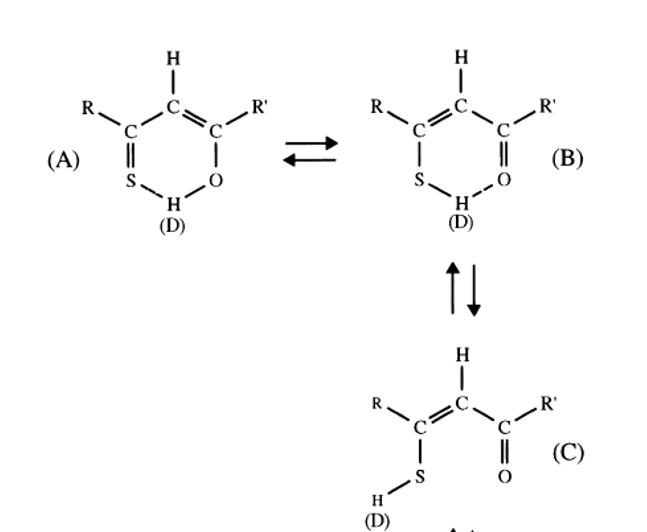
Figure 4.  β-thixoketones.  With R and R` equal to CH₃ it is thioacetylacetone. D is referring to deuteriation (see isotope effects).

Table 1.  Chemical shifts of thioacetylacetone from Ref. 2.

1. Estimated by comparison with model compounds

It is of course important to know the chemical shifts of the two tautomers.  Chemical shifts for one of the two can normally  be obtained from solid state NMR spectra. ^[3] Model compounds have also been suggested, but in that case the monitoring atom has to be far from the site of tautomeric action. ^[4] The chemicals shifts of both tautomeric species may be estimated from theoretical calculations (see later).

¹⁹F chemical shifts

The very large chemical shift range of ¹⁹F makes it well suited for detecting of tautomeric equilibria.  A good example is fluorosubstituted o-hydroxyazo compounds (see Figure 5). ^[4] 

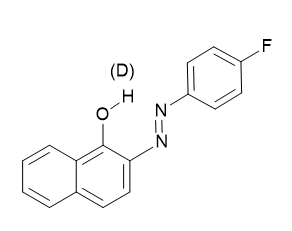
Figure 5.  Only one tautomer is shown.  For deuterium isotope effects on ¹⁹F chemical shifts see later.

Other examples are  fluorosubstituted fuchsones and benzaurins ^[5]  or fluoro-X-benzofurans. ^[6]

Also ¹³C-¹⁹F coupling constants may be used in the characterization of tautomeric systems.^[7] This is building on the fact the one-bond C-F coupling depend strongly on the double character of the C-F bond.

¹⁷O chemical shifts

The ¹⁷O resonances suffer from broad lines, but this is normally compensated by the very large chemical shift range. ^[8]  Examples of b-diketones and 1,8-dihydroxy2-acetyl, 3,6-dimethylnaphthalene are given in Ref. ^[9]

Coupling constants

A much used parameter is the ¹J(N,H) in nitrogen containing compounds with an NH motif.  This type of coupling is typically around 90 Hz. ^{[10]  1}J(N,H) can be used in all compounds containing an NH group taking part in tautomerism.  A typical examples is “ o-hydroxy Schiff bases”  see Figure 6. ^[10]

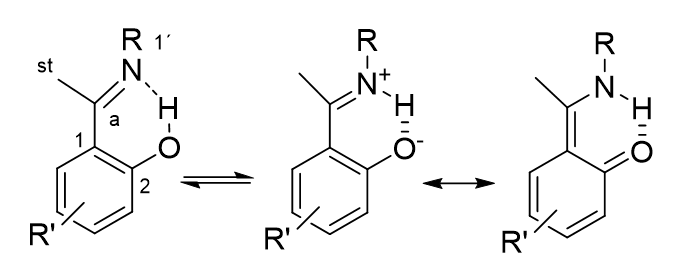
Figure 6.  o-Hydroxy Schiff bases.

A typical problem to consider is NH exchange with the surrounding leading to too small coupling constants. Temperature studies may be helpful in eliminating this problem.  For cases in which suitable model compounds are not available, ¹J(N,H) can be predicted based on calculated NH bond lengths. ^[11]

Isotope effects on chemical shifts

Two types of isotope effects on chemical shifts, primary and secondary can be applied. They are  defined as follows in case of deuterium as the isotope : primary , ^PΔH(D) = δH-δD and secondary, ⁿΔX(D) = δX(H)-δX(D).  n is the number of bonds between the deuterium and the atom in question, X.   The most common isotope to be used is deuterium, as also indicated in the definition. In case of an equilibrium, the isotope effects are different from the so called intrinsic isotope effects, which are found in “static” cases.

Equilibrium isotope effects

The definition of the equilibrium isotope effects  is expressed as:

ΔX_H(D) x (δC_M- δC_PT)    in which ΔX_H(D  is the change in the equilibrium upon deuteriation.  The full equation was given early on by Bordner et al. ^[12] : 

ΔC(D) =  (δC_A - δC_B ) x (a - a_D ) + [a_D x ΔC_A(D)_i + (1-  a_D ) x ΔC_B(D) _i]                      Eq.1

The first term in this equation corresponds to the equilibrium isotope effect, whose magnitude depends on the change in the position of  equilibrium (a - a_D ) due to substitution of H by D and on the difference in the magnitude of the chemical shifts of the given carbon in the  A and B forms.  The second term represents the direct effect of the isotopic substitution on the chemical shifts  (intrinsic isotope effect, ΔC(D)_i ).  The equilibrium term is a consequence of the potential energy diagram Figure 7.  Deuteriation will in a double well potential lead to a change in the equilibrium.  This means that the chemical shift difference comes into play multiplied with the change in the equilibrium upon deuteriation (see Eq. 1)

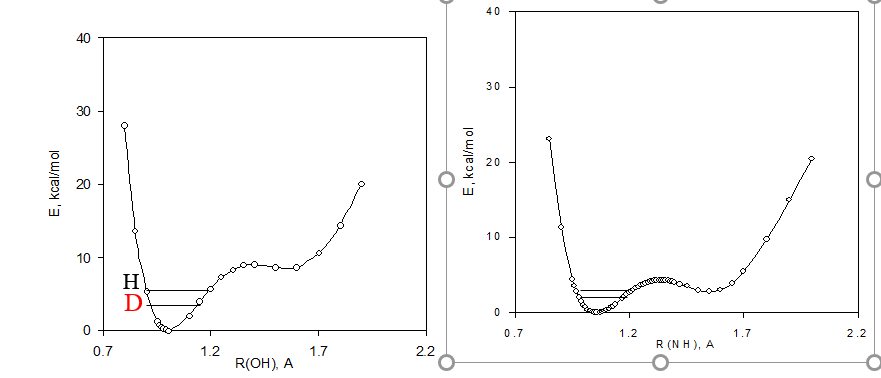
Figure 7.  Potential energy diagrams including zero point energies for H and d species for a tautomeric equilibrium of o-hydroy Schiff  bases.

The Limbach group has used an approach based on bond valences.  See e.g. Ref. ^[13]

Reviews dealing with equilibrium isotope effects can be found. ^{[11][14][15][16][17][18]}

Primary deuterium isotope effects

The sign of the primary deuterium isotope effect can be used to estimate hydrogen bond strength.  Positive primary isotope effects are for weak to medium strong isotope effects, whereas a negative isotope effects was claimed to be an indicator of a strong hydrogen bond. ^[19] However, if equilibrium is occurring positive as well as negative effects may occur. ^[11]

Secondary deuterium isotope effects

Deuterium isotope effects on ¹³C chemical shifts

Secondary deuterium isotope effects have a characteristic S-shaped dependence if plotted vs. the mole fraction as illustrated in Figure 8. ^[20]  It is also obvious that at the maximum and minimum the changes will be minimal, whereas they will be large and of different sign at the edges (small and large mole fractions).

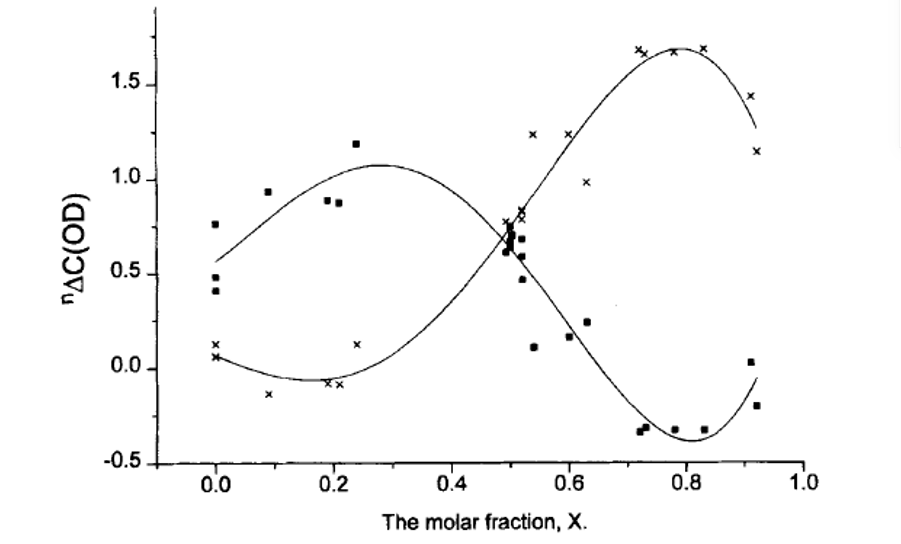
Figure 8.  Plot of two-bond deuterium isotope effects of ¹³C chemical shifts vs. mole fraction.  From Ref. 20 with Permission from Wiley-VCH.

Lifting degeneracy in symmetrical systems

¹³C NMR.   Deuterium isotope effects on ¹³C chemical shifts can in a very elegant way be used to detect an equilibrium.  The technique was originally invented in the study of carbonium ions. ^[21] A typical example of this technique is seen in Figure 9.  The origin of the effect is the difference in CH stretching frequencies of the aldehyde, 2770 cm^-1 and the enol type, 3020 cm^-1.

Figure 9.  Lifting of degeneracy by deuterium substitution. ^[22]

¹⁸O has been used as the isotope in order to distinguish between double well and symmetric hydrogen bond potentials in compounds having strong intramolecular hydrogen bonds between carboxylic acid and carboxylate groups. Figure 10. ^[23]

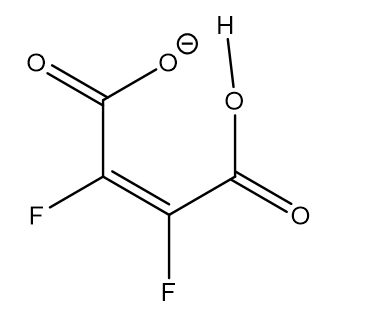
Figure 10.  ¹⁸O labelled maleic anion.

What is the characteristics of equilibrium isotope effects?  They can be measured at nuclei far from the site of isotope substitution and can be very large.  In case of thioacetylacetone (Figure 4) deuteriation at the OH;SH position leads to ¹³C isotope effects at the “CS” carbon as large as -10.5 ppm depending on temperature. ^[2]  Furthermore, as seen from Eq.  1 they will in those cases that they are larger than the intrinsic ones be proportional to the chemical shift difference between the nuclei in question (the chemical sift differences can be estimated from DFT calculations of NMR nuclear shieldings). An example of the latter is shown in Table 2.

Table 2. Calculated ¹³C nuclear shieldings for the Schiff base 2-(N-methyl-α-iminoethyl)-3,5-dibromophenol (Figure 6 with R= CH₃ and  R´= 3,5-dichloro)

From the above table we can predict that all carbons except C-4, C-6 and Cst will show large equilibrium isotope effects.

In addition, the ratio between isotope effects can be expressed in those cases in which the equilibrium isotope effects dominate:

ΔC-1/ ΔC-2 = (δC-1_M- δC-1_PT)/ (δC-2_M- δC-2_PT)

This shows the ratio between isotope effects for C1 and C2 of the two tautomers called M and PT.

An illustration is given in Figure 11 for a series of o-hydroxy Schiff bases (Figure 5). ^[7]

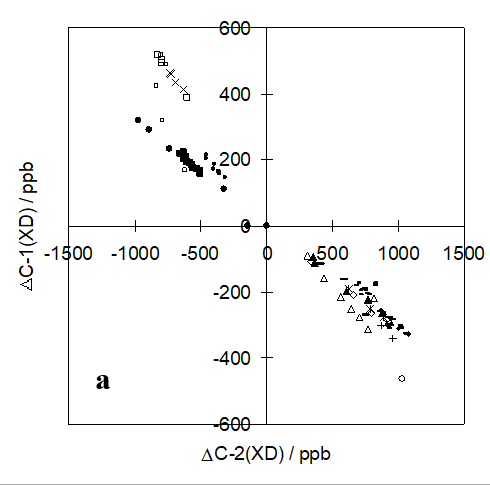
Figure  11. Ratios between deuterium isotope effects on ¹³C chemical shifts for C-1 and C-2 for a series of o-hydroxy Schiff bases. Taken from Ref. ^[7] with permission from the American Chemical Society.

Deuterium isotope effects on ¹⁹F chemical shifts

These have been demonstrated in o-hydroxyazo compounds  (see Fig. 6). However, in the benzene derivative case no tautomerism is taking pIace ,the  isotope effect is only 0.011 ppm, whereas in similar naphthalene derivatives the effects in the equilibrium case is 0.077 ppm or 0.123 ppm For the azo group in 1- respective 2-position. ^[24]

Deuterium isotope effects on ¹⁷O chemical shifts

These isotope effects are large at both oxygens involved (Figure 12). ^[9]

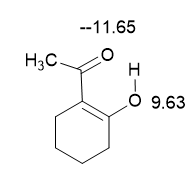
Figure 12.  Deuterium isotope effects on ¹⁷O chemical shifts.  Only one of the tautomers is shown.

Determination of equilibrium constants

As NMR parameters, chemical shifts and coupling constants, are average ones, the equilibrium constants can be determined, if we have determined the corresponding parameters for the two tautomers.  Furthermore, as described in Figure 8 the mole fractions can be determined from deuterium isotope effects on 13C chemical shifts.