Cellular Automata in Modeling and Predicting Urban Densification: Comparison
View Latest Version
Please note this is a comparison between Version 3 by Dean Liu and Version 2 by Dean Liu.

The creation of an accurate simulation of future urban growth is considered to be one of the most important challenges of the last five decades that involves spatial modeling within a GIS environment. Even though built-up densification processes, or transitions from low to high density, are critical for policymakers concerned with limiting sprawl, the literature on models for urban study reveals that most of them focus solely on the expansion process. Although the majority of these models have similar goals, they differ in terms of implementation and theoretical assumptions. Cellular automata (CA) models have been proven to be successful at simulating urban growth dynamics and projecting future scenarios at multiple scales.

  • cellular automata
  • urban densification
  • urban models

1. Introduction

Urbanization is a multifaceted, worldwide process that reveals itself in rapidly changing human population densities and shifting land-use patterns. In the last 30 years, there has been a rapid growth in urban expansion owing primarily to development policies that prioritized urban growth over agricultural and rural development. Large-scale immigration to cities has resulted in rapid urbanization and land-use change [1]. Accelerating urbanization has put a strain on land resources and resulted in a slew of environmental and social issues [2]. In different countries, the shape or pattern of urban growth varies greatly, but in general, city growth is a twofold process of external expansion and rapid physical growth or internal growth and reorganization [3]. This can be further subdivided into two categories: Urban expansion, which deals with horizontal growth and urban densification; or infill development, which is referred as vertical expansion or in-between development [4].
Globally, many cities and regions have enacted policies aimed at encouraging urban densification through a combination of spatial planning and fiscal or economic measures, as well as encouraging infill development and land recycling [5][6]. Urban densification, through infill development, is frequently addressed in urban planning literature as a possible approach to produce compact communities, curb sprawl, and establish urban sustainability [7][8][9]. For more efficient planning and management, a greater understanding of the process of urban densification and the implications of this growth and land-use change is essential [10]. As a result, several empirical and theoretical modeling tools for the simulation and prediction have recently been developed [11][12].
Urban densification is influenced by various driving factors such as those related to the natural environment, socioeconomics, the built environment, and governance policies, thus making modeling of urban growth complex [13]. Due to their simplicity, versatility, and intuitiveness, CA-based models have been widely used [14]. The application of cellular space models to geographic modeling dates backs to the 1980s [15][16][17]. Building on these ideas and owing to the fact that new generations of hardware and software to simulate CA have been improved upon since the 1900s, a generic modeling framework based on discrete-time, cell-spaced models was proposed for cellular computation [18][19]. Transition rules are used to calculate development probability as a function of neighborhood, a series of geographical parameters, and stochastics disturbance terms which form the base of CA [1][20][21]. Furthermore, CA is highly compatible with the GIS environment. The nature in which CA works has a natural affinity with raster data, as both treat the input as a representation of cells. As a result of this, ref. [22] stated that CA has a high computational and operational efficiency, and that the neighborhood function has an analogous relationship to focal sum or focal mean function, making it suitable for any kind of simulation. These inherent similarities with GIS helped geographers to quickly adopt it as a framework for modeling spatial dynamics [23][24].
Hence, the nature of the CA model to explicitly consider the spatiotemporal dynamics of urban growth makes it more advantageous than other existing models [25]. Recently, there have been many other developments, such as hybrid CA urban models, which incorporate artificial intelligence based on empirical data such as artificial neural networks [26], case-based reasoning (CBR) [27], and colony optimization [28].The increasing uncertainty due to rapid environmental and societal and technological changes makes it crucial to explore multiple urban models, and driving factors have become important. With urban densification being an innovative yet crucial component of global environmental change, researchers reviewed the CA model in detail, including various integration approaches with other urban models. Moreover, the CA model facilitates movement toward an environment-sensitive modeling [29] which can be used to establish future development pillars and can be utilized to resolve any limitations or shortcomings.

2. Cellular Automata (CA) Model

Cellular automata (CA) are computational methods for simulating the growth of a complex system by describing it with a set of simple rules [30]. It is a system of cells representing a discrete moment and a set of rules, determining the local transfer function based on the current state of an adjacent cell [31]. In the modeling of urban processes, CA models have a number of advantages, including the ability to perform spatial dynamics and time explicitly [32]. Wagner [33] proposed that CA can be considered an analytical engine of GIS after successfully analyzing the similarities and capabilities of CA. Sgandurra [34] defined a cell as the smallest unit of space made up of only one component. Each cell in the lattice structure known as cellular space is in one of several predetermined states. The law guiding the change between states is known as the local rule. It is particularly important to choose the optimum transition rules for the phenomenon being studied [35]. Since a cell’s finite state machine only accepts input from the neighborhood, it is referred to as “local” in this definition. The term “neighborhood” refers to the cells that are immediately adjacent to a certain cell, and they have the power to affect the subsequent state of that cell. Thus, different states with a CA transition rule will yield different results, but will be similar in statistical form [36]. Understanding the nature of the spatial dynamic requires the use of dynamic models as well as social, economic, and environmental concepts [37]. Over the past few decades, there has been a substantial advancement in various modeling techniques to understand urban expansion [38]. Various simulation and prediction methods have been used in the past to simulate future expansion and a few studies considered densification [39][40][41].

3. Cellular Automata in Urban Densification

The introduction and implementation of CA models designed to simulate urban land-use change from a bottom-up perspective has radically altered the study of urban systems over the last four decades. While models (in general) are abstractions of reality, few attempts have been made to capture the wider chaotic dynamics of urban densification to date [42]. Due to CA models’ inability to represent entities at the most disaggregated levels, current urban models focus on horizontal urban growth. Recent studies [43][44] have made it more evident that CA-based urban models mainly focus on urban sprawl and expansion. Traditionally, CA models simulate the spatiotemporal dynamics of land-use structures using grid units that are the same size as a cell lattice, similar to raster pixels or patches [45]. The transition rule is the most significant element in the CA model, and researchers have utilized a variety of methods, such as artificial neural networks [46], genetic algorithms [47], Markov models [48], the Bayesian method [49], kernel functions [28], and support vector machines [50] to produce transition rules. Vertical urban growth or urban densification is one of the most essential parts of ‘sustainable, low carbon, equitable, resilient development’, as it changes the operation of cities even more [51]. Furthermore, building distribution patterns can have a substantial impact on the nature of the urban heat island effect [52] and can increase pollution levels [53] and road traffic noise levels [54]. Even though CA models for urban densification have recently emerged, there have been studies about 3D CA models [55] which provide an even more realistic representation. As a result, spatial and local variables should be added in order to increase the accuracy of CA simulation [56]. It is significant to understand the various types of drivers and constraints underlying the urban CA models. This would help urban CA modelers to understand the relation between global patterns and local actions, thus acting as a vehicle to construct and validate a new urban model based on “what-if” decision making. CA urban models should also consider qualitative factors such as land ownership and density change by adjusting the models’ parameter settings. There have been few works carried out with CA and densification in recent years, but the number is insignificant, as seen in the Figure 61. As a result of which, it is crucial to review CA-based urban study scenarios based on the data collected, driving factors, and the undergoing process which produces an accurate model. This can open several possibilities and the necessity to expand the horizon of studying different aspects of urban densification.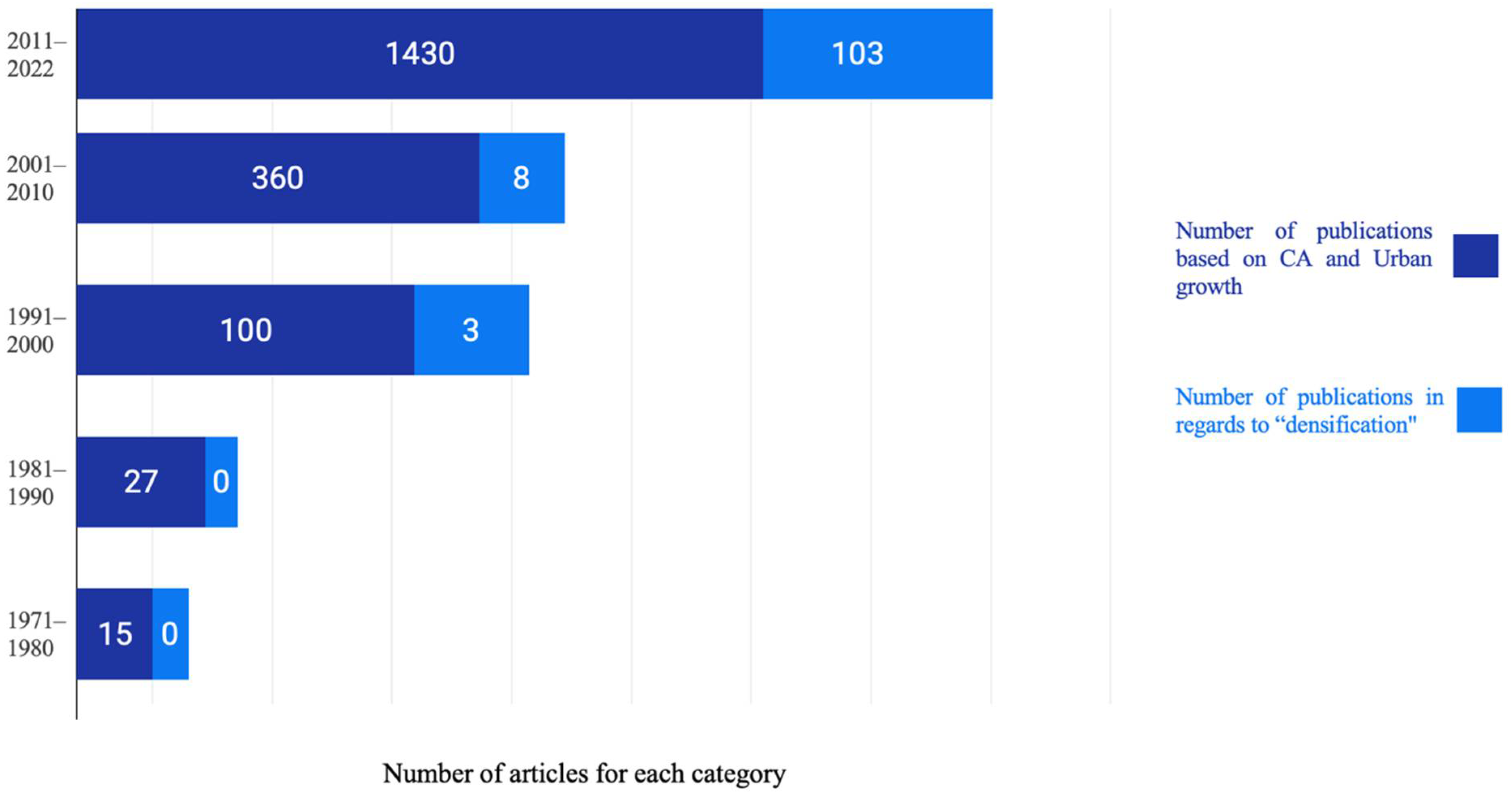
Figure 61. Total number of stud

References

  1. Liu, X.; Ma, L.; Li, X.; Ai, B.; Li, S.; He, Z. Simulating urban growth by integrating landscape expansion index (LEI) and cellular automata. Int. J. Geogr. Inf. Sci. 2014, 28, 148–163.
  2. Lambin, E.F.; Turner, B.L.; Geist, H.J.; Agbola, S.B.; Angelsen, A.; Bruce, J.W.; Coomes, O.T.; Dirzo, R.; Fischer, G.; Folke, C. The causes of land-use and land-cover change: Moving beyond the myths. Glob. Environ. Chang. 2001, 11, 261–269.
  3. Rasoul, G.; Noushad, S. Smart growth strategy in urban development, principles and approaches. J. Geogr. Develop. 2008, 6, 163–180.
  4. Shi, L.; Shao, G.; Cui, S.; Li, X.; Lin, T.; Yin, K.; Zhao, J. Urban three-dimensional expansion and its driving forces—A case study of Shanghai, China. Chin. Geogr. Sci. 2009, 19, 291–298.
  5. Teller, J. Regulating urban densification: What factors should be used? Build. Cities 2021, 2, 302–317.
  6. Mustafa, A.M.; Heppenstall, A.; Omrani, H.; Saadi, I.; Cools, M.; Teller, J. Modelling built-up expansion and densification with multinomial logistic regression, cellular automata and genetic algorithm. Comput. Environ. Urban Syst. 2018, 67, 147–156.
  7. Gordon, P.; Richardson, H.W. Are compact cities a desirable planning goal? J. Am. Plan. Assoc. 1997, 63, 96–106.
  8. Kaur, M.; Hewage, K.; Sadiq, R. Investigating the impacts of urban densification on buried water infrastructure through DPSIR framework. J. Clean. Prod. 2020, 259, 120897.
  9. Broitman, D.; Koomen, E. Residential Density Change: Densification and Urban Expansion. Geogr. Urban Process. (Sub-Top.) 2015, 54, 32–46.
  10. Leao, S.; Bishop, I.; Evans, D. Simulating urban growth in a developing nation’s region using a CA-based model. J. Urban Plan. Dev. 2004, 130, 145–158.
  11. Herold, M.; Goldstein, N.C.; Clarke, K.C. The spatiotemporal form of urban growth: Measurement, analysis and modeling. Remote Sens. Environ. 2003, 86, 286–302.
  12. Poelmans, L.; Van Rompaey, A. Detecting and modelling spatial patterns of urban sprawl in highly fragmented areas: A case study in the Flanders–Brussels region. Landsc. Urban Plan. 2009, 93, 10–19.
  13. Wang, H.; He, S.; Liu, X.; Dai, L.; Pan, P.; Hong, S.; Zhang, W. Simulating urban expansion using a cloud-based cellular automata model: A case study of Jiangxia, Wuhan, China. Landsc. Urban Plan. 2013, 110, 99–112.
  14. Santé, I.; García, A.M.; Miranda, D.; Crecente, R. Cellular automata models for the simulation of real-world urban processes: A review and analysis. Landsc. Urban Plan. 2010, 96, 108–122.
  15. Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240.
  16. Couclelis, H. Cellular Worlds: A Framework for Modeling Micro—Macro Dynamics. Environ. Plan. A 1985, 17, 585–596.
  17. Phipps, M. Dynamical Behavior of Cellular Automata under the Constraint of Neighborhood Coherence. Geogr. Anal. 2010, 21, 197–215.
  18. Batty, M. Urban Evolution on the Desktop: Simulation with the Use of Extended Cellular Automata. Environ. Plan. A 1998, 30, 1943–1967.
  19. Aburas, M.M.; Ho, Y.M.; Ramli, M.F.; Ash’aari, Z.H. The simulation and prediction of spatio-temporal urban growth trends using cellular automata models: A review. Int. J. Appl. Earth Obs. GeoInf. 2016, 52, 380–389.
  20. Liang, X.; Liu, X.; Li, D.; Zhao, H.; Chen, G. Urban growth simulation by incorporating planning policies into a CA-based future land-use simulation model. Int. J. Geogr. Inf. Sci. 2018, 32, 2294–2316.
  21. Tong, X.; Feng, Y. A review of assessment methods for cellular automata models of land-use change and urban growth. Int. J. Geogr. Inf. Sci. 2020, 34, 866–898.
  22. Al-sharif, A.; Pradhan, B. A novel Approach for Predicting the Spatial Patterns of Urban Expansion by Combining the Chi-Squared Automatic Integration Detection Decision Tree, Markov Chain, and Cellular Automata Models in GIS. Geocarto Int. 2015, 30, 858–881.
  23. Singh, A.K. Modelling Land Use Land Cover Changes Using Cellular Automata in a Geo-Spatial Environment. Master’s Thesis, ITC, Enschede, The Netherlands, 2003.
  24. Liu, Y. Modelling Urban Development with Geographical Information Systems and Cellular Automata: A Case Study of Sydney since 1971; Taylor and Francis: New York, NY, USA, 2001.
  25. Basse, R.; Omrani, H.; Charif, O.; Gerber, P.; Bódis, K. Land use changes modelling using advanced methods: Cellular automata and artificial neural networks. The spatial and explicit representation of land cover dynamics at the cross-border region scale. Appl. Geogr. 2014, 53, 160–171.
  26. Li, X.; Yeh, A.G.O. Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 2002, 16, 323–343.
  27. Li, X.; Liu, X.P. An extended cellular automaton using case-based reasoning for simulating urban. Int. J. Geogr. Inf. Sci. 2006, 20, 1109–1136.
  28. Liu, X.; Li, X.; Liu, L.; He, J.; Ai, B. A bottom-up approach to discover transition rules of cellular automata using ant intelligence. Int. J. Geogr. Inf. Sci. 2008, 22, 1247–1269.
  29. Mitsova, D.; Shuster, W.; Wang, X. A cellular automata model of land cover change to integrate urban growth with open space conservation. Landsc. Urban Plan. 2011, 99, 41–153.
  30. Mantelas, L.; Prastacos, P.; Hatzichristos, T.; Koutsopoulos, K. Using fuzzy cellular automata to access and simulate urban growth. GeoJournal 2012, 77, 13–28.
  31. Liu, Y.; Feng, Y. A Logistic Based Cellular Automata Model for Continuous Urban Growth Simulation: A Case Study of the Gold Coast City, Australia. In Agent-Based Models of Geographical Systems; Heppenstall, A., Crooks, A., See, L., Batty, M., Eds.; Springer: Dordrecht, The Netherlands, 2012.
  32. Al-Shalabi Al-Sharif, A.A.; Pradhan, B. Monitoring and predicting land use change in Tripoli Metropolitan City using an integrated Markov chain and cellular automata models in GIS. Arab. J. Geosci. 2013, 7, 4291–4301.
  33. Wagner, D.F. Cellular Automata and Geographic Information Systems. Environ. Plan. B Plan. Des. 1997, 24, 219–234.
  34. Sgandurra, D. An Introduction to Cellular Automata (Powerpoint presentation); Bio-inspired Models of Computation, Dipartimento di Informatica, Università di Pisa: Pisa, Italy, 16 October 2009.
  35. Rodríguez Puente, R.; Pérez Betancourt, Y.G.; Mufeti, K. Cellular Automata and Its Applications in Modeling and Simulating the Evolution of Diseases ; National Research Symposium: Windhoek, Namibia, 2015.
  36. Wolfram, S. Cellular automata as models of complexity. Nature 1984, 311, 419–424.
  37. Grimm, N.; Grove, M.; Pickett, S.T.A.; Redman, C. Integrated Approaches to Long-Term Studies of Urban Ecological Systems; Springer: Boston, MA, USA, 2008.
  38. Allen, J.; Lu, K. Modeling and Prediction of Future Urban Growth in the Charleston Region of South Carolina: A GIS-based Integrated Approach. Conserv. Ecol. 2003, 8.
  39. Amato, F.; Pontrandolfi, P.; Murgante, B. Using Spatiotemporal Analysis in Urban Sprawl Assessment and Prediction. In Computational Science and Its Applications–ICCSA 2014. ICCSA 2014. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8580, pp. 758–773.
  40. Verburg, P.; Overmars, K.; Huigen, M.; Groot, W.; Veldkamp, A. Analysis of the effects of land use change on protected areas in the Philippines. Appl. Geogr. 2006, 26, 153–173.
  41. Jokar Arsanjani, J.; Zipf, A.; Mooney, P.; Helbich, M. An Introduction to OpenStreetMap in Geographic Information Science: Experiences, Research, and Applications. In OpenStreetMap in GIScience; Jokar Arsanjani, J., Zipf, A., Mooney, P., Helbich, M., Eds.; Lecture Notes in Geoinformation and Cartography; Springer: Cham, Switzerland, 2015.
  42. Arsanjani, J.J.; Barron, C.; Bakillah, M.; Helbich, M. Assessing the quality of OpenStreetMap contributors together with their contributions. In Proceedings of the AGILE, Leuven, Belgium, 14–17 May 2013; pp. 14–17.
  43. Liu, Y.; Batty, M.; Wang, S.; Corcoran, J. Modelling urban change with cellular automata: Contemporary issues and future research directions. Prog. Hum. Geogr. 2019, 45, 3–24.
  44. Musa, S.I.; Hashim, M.; Reba, M.N. A review of geospatial-based urban growth models and modelling initiatives. Geocarto Int. 2017, 32, 813–833.
  45. Aburas, M.M.; Ho, Y.; Ramli, M.F.; Ash’aari, Z.H. Improving the capability of an integrated CA-Markov model to simulate spatio-temporal urban growth trends using an Analytical Hierarchy Process and Frequency Ratio. Int. J. Appl. Earth Obs. Geoinf. 2017, 59, 65–78.
  46. Clarke, K.; Gaydos, L. Loose-Coupling a Cellular Automaton Model and GIS: Long-Term Urban Growth Prediction for San Francisco and Washington/Baltimore. Int. J. Geogr. Inf. Sci. IJGIS 1998, 12, 699–714.
  47. Mustafa, A.M.; Rompaey, A.V.; Cools, M.; Saadi, I.; Teller, J. Addressing the determinants of built-up expansion and densification processes at the regional scale. Urban Stud. 2018, 55, 3279–3298.
  48. Kang, J.; Fang, L.; Li, S.; Wang, X. Parallel Cellular Automata Markov Model for Land Use Change Prediction over MapReduce Framework. ISPRS Int. J. Geo-Inf. 2019, 8, 454.
  49. Yang, Q.; Li, X. Nonlinear transition rules of urban cellular automata based on a Bayesian method. Acat Sci. Nat. Univ. Sunyatseni 2007, 46, 105–109. (In Chinese)
  50. Yang, Q.; Li, X.; Shi, X. Cellular automata for simulating land use changes based on support vector machines. Comput. Geosci. 2008, 34, 592–602.
  51. Palme, M.; Ramirez, J.E. A Critical Assessment and Projection of Urban Vertical Growth in Antofagasta, Chile. Sustainability 2013, 5, 2840–2855.
  52. Huang, C.; Homer, C.; Yang, L. Regional forest land cover characterisation using medium spatial resolution satellite data. In Remote Sensing of Forest Environments; Springer: Boston, MA, USA, 2003; pp. 389–410.
  53. Aristodemou, E.; Boganegra, L.M.; Mottet, L.; Pavlidis, D.; Constantinou, A.; Pain, C.C.; Robins, A.; ApSimon, H.M. How tall buildings affect turbulent air flows and dispersion of pollution within a neighbourhood. Environ. Pollut. 2018, 233, 782–796.
  54. Tang, U.W.; Wang, Z.S. Influences of urban forms on traffic-induced noise and air pollution: Results from a modelling system. Environ. Model. Softw. 2007, 22, 1750–1764.
  55. Koziatek, O.; Dragićević, S. iCity 3D: A geosimualtion method and tool for three-dimensional modeling of vertical urban development. Landsc. Urban Plan. 2017, 167, 356–367.
  56. Jian, S.U.N.; Zhang, L.; Chunlu, P.E.N.G.; Zhongren, P.E.N.G.; Meng, X.U. CA-based urban land use prediction model: A case study on orange county, Florida, US. J. Transp. Syst. Eng. Inf. Technol. 2012, 12, 85–92.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback