Classical Nucleation Theory: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Catherine Yang and Version 1 by Zhou Jianmin.

Crystal nucleation determining the formation and assembly pathway of first organic materials is the central science of various scientific disciplines such as chemical, geochemical, biological, and synthetic materials. Classical nucleation theory (CNT)  applies to systems of small organic molecules with an emphasis on the molecular interpretation of nucleation kinetics. CNT holds that density fluctuations are concomitant with the development of crystalline order. In other words, a crystal nucleus has an identical structure to its bulk crystal. 

  • crystal nucleation
  • solution chemistry
  • polymorphism

1. Thermodynamics

CNT was originally derived from the pioneering work of Fahrenheit on the supercooling of water in the early 1700s. It was endowed with thermodynamic underpinnings by Gibbs in the late 1800s on the studies of droplet formation on a supersaturated vapor. In the early 1900s, Volmer and Weber, and others formulated the kinetic aspects of CNT for vapor condensation; subsequently, they were extended by Turnbull and Fisher in the 1950s to address the cases of nucleation in condensed phases [45][1].
Nucleation is the first step of the phase transition that occurs by local density fluctuations of the old phase from a supersaturated state [11][2]. The path by which the phase transition takes place is often described by the cluster approach. A cluster of a certain number n of molecules (or building units) may be formed rarely because of a free-energy barrier presented in the course of cluster formation (Figure 1a). The barrier results from the competition in the growing clusters between the gain in bulk free energy (∆Gv = −n∆μ) due to the addition of a molecule and the increasing surface free energy (∆Gs = aγ) via the creation of the additional crystal-liquid interface with specific interfacial free energy, γ, and a surface area, a. The total free energy is thus given by
ΔG=ΔGv+ΔGs=−nΔμ+aγ  (1) Δ G = Δ G v + Δ G s = − n Δ μ + a γ
Δμ=μl−μs=kBTlnS             (2)
S=c/c0                               (3)
a=A(v0n)2/3                               (4) Δ μ = μ l − μ s = k B T ln S
S = c c 0
a = A ( v 0 n ) 2 / 3
where kB is the Boltzmann constant, T is the absolute temperature, S is the solution supersaturation ratio, c is the actual concentration, c0 is the equilibrium (saturated) concentration, A is a shape factor, and v0 is the molecular volume in the crystalline phase.
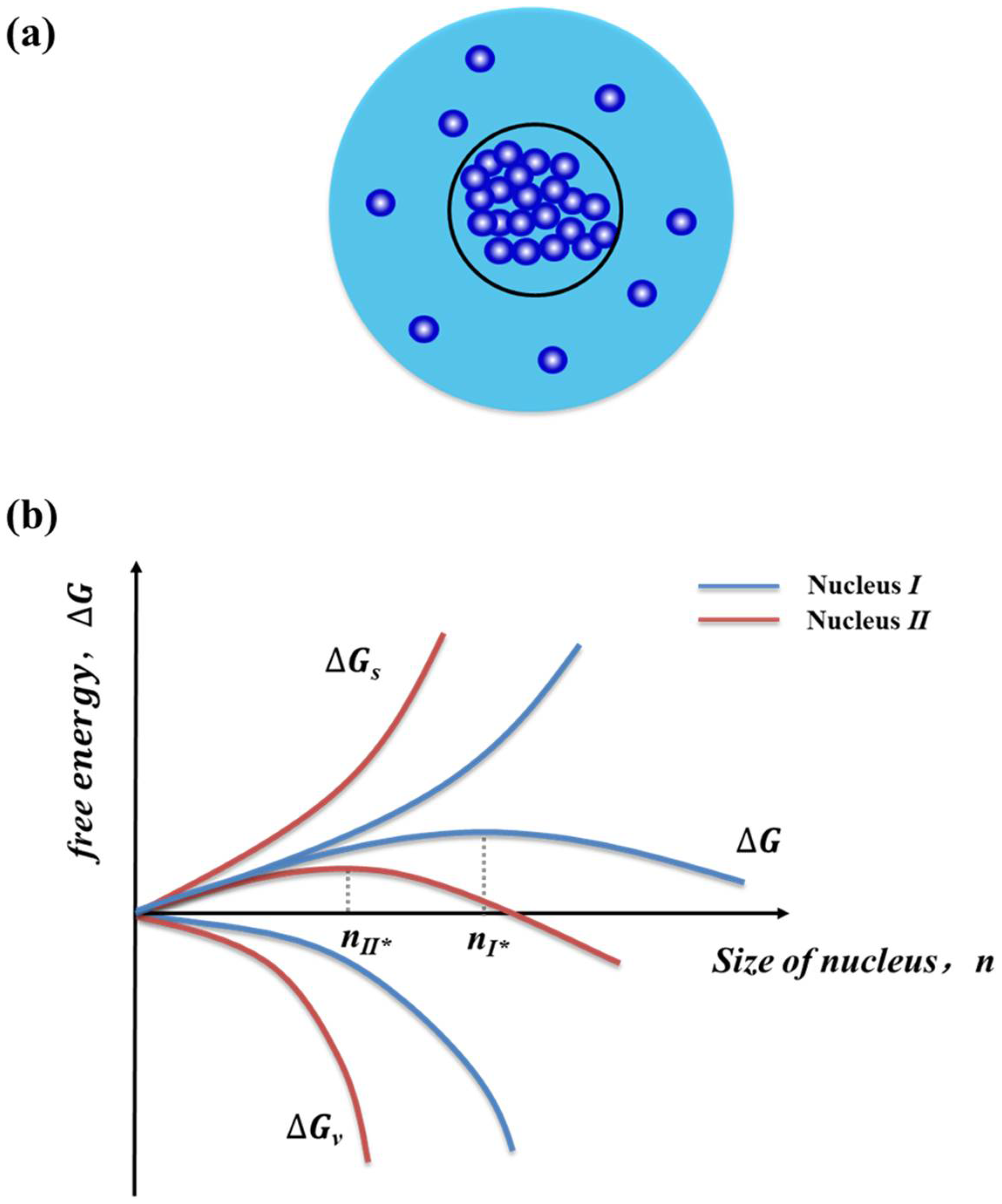
Figure 1. Cluster formation and the associated changes of free energy during crystal nucleation. (a) Nanoscopical formation of new phase via molecular clustering and (b) free energy diagram of crystal nucleation showing the formation of critical nucleus size and supersaturation influence wherein a high supersaturation in the solution leads to a lower critical size of the nucleus (i.e., n∗I  n I * > n∗II n II * ).
When the size of a cluster is small, the contribution of the surface free energy will be dominant over the bulk free energy, and the cluster will tend to dissolve. However, the bulk free energy will become dominant for the clusters with relatively large sizes. Therefore, a critical size of cluster (n*, also named as nucleus) exists, beyond which the cluster probably survives from dissolution and becomes a nucleus growing further (Figure 1b) [46][3]. The critical size of a nucleus and the critical nucleation barrier (∆Gc) were given by
n∗=8c3v02γ3/27(kBTlnS)3             (5) n * = 8 c 3 v 0 2 γ 3 27 ( k B T l n S ) 3
ΔGc=4c3v02γ3/27(kBTlnS)2         (6) Δ G c = 4 c 3 v 0 2 γ 3 27 ( k B T l n S ) 2
The size of a critical nucleus is dependent upon the strength of free energy barrier, which is influenced by crystallization conditions such as supersaturation, solvent, and temperature [13][4]. Higher levels of solution supersaturations (i.e., greater driven force) leads to the lower free energy barrier and thus the lower size of the critical nucleus. The critical clues and the size-dependence on the thermodynamic driving force have been recently demonstrated experimentally [47][5].

2.2. The Kinetics of Crystal Nucleation

2. The Kinetics of Crystal Nucleation

Resembling the kinetic theory of reaction, the steady-state rate of nucleation (J), which is defined as the number of nuclei per unit time per unit volume, is expressed in the form of the Arrhenius rate equation:
J=Aexp(−ΔGc/kBT)           (7) J = A exp − Δ G c k B T
where A is the pre-exponential factor. Equation (6) can be rewritten as
J=Aexp(−Bln2S)               (8) J = A exp ( − B l n 2 S )
B=4c3γ3v02/27(kBT)3          (9) B = 4 c 3 γ 3 v 0 2 27 k B T 3
Here B represents the thermodynamic parameter. Equation (8) is valid for homogenous nucleation from the solution. In the case of heterogeneous nucleation, the interfacial energy γ should be replaced by an effective interfacial energy γHEN = φγ, where the activity factor of template substrate, φ, is in the range of 0 to 1, dependent upon the wetting ability of a cluster with the substrate surface. Note that in the case of homogeneous nucleation, the interfacial free energy represents an average over different crystal planes. More discussions on heterogeneous nucleation can be found in a book by Kashchiev [11][2].
The nucleation kinetics is controlled by the frequencies fn* and gn* of monomer attachment and detachment from an n*-sized cluster, respectively. In a stationary state of the nucleation process with a constant concentration Xn of n-size clusters, the nucleation rate was defined as the difference between the transformation frequency fn*Xn* of the nuclei (n*) into the smallest super-nuclei (n* + 1) and detachment frequency gn*+1Xn*+1 of the super-nuclei n* + 1 into the nuclei n*:
J=fn*Xn*−gn*+1Xn*+1=ξfn*Xn*          (10) J = f n * X n * − g n * + 1 X n * + 1 = ξ f n * X n *
ξ=1−gn*+1Xn*+1/fn*Xn*                      (11) ξ = 1 − g n * + 1 X n * + 1 f n * X n *
With f* ≡ fn*, X* ≡ Xn*, Equation (9) is rearranged into a familiar form
J=zf∗C∗                                                     (12) J = z f * C *
z=ξX∗/C∗=ln2S/√12πB                (13) z = ξ X * C * = l n 2 S 12 π B
where z is the Zeldovich factor accounting for the use of C* instead of the actual nucleus concentration X* and for those clusters larger than nuclei but eventually decay rather than grow into macroscopic crystals. C* = C0exp(−∆Gc/kBT) is the equilibrium concentration of crystal nuclei. C0 is the concentration of nucleation sites in the system and is assumed equal to 1/v0 for homogenous nucleation (v0 is the volume of a single solute molecule).
The nucleation rate was thus determined by not only the nucleation barrier ∆Gc and the concentration C0 of nucleation sites but also the attachment frequency f* of monomers to the nucleus. According to Equations (7), (11), and (12), the pre-exponential factor zf*C0 is related to molecular attachment events of monomers to the critical nucleus. The kinetic attachment over the course of nucleation could be controlled either by the volume diffusion process of monomers in solution towards the nucleus or by the interfacial transfer of monomers across the interface of the crystal nucleus and the surrounding solution.
When volume diffusion was the rate-determining step in monomer attachment to the nucleus, f* = j*S* wherein S* is the surface area of a nucleus and j* is the diffusion flux of monomers to the nucleus surface. By the assumption of a spherical shape, the radius of a nucleus:
r∗=(3v0n∗/4π)1/3                                                                  (14) r * = ( 3 v 0 n * / 4 π ) 1 / 3
The flux j* = DC/r* and f* is given by
f∗=(48π2v0)1/3DCn*1/3=(48π2v0)1/3Dn*1/3C∗S                      (15) f * = ( 48 π 2 v 0 ) 1 / 3 D C n * 1 / 3 = ( 48 π 2 v 0 ) 1 / 3 D n * 1 / 3 C * S
where D is the diffusion coefficient of monomers and C is the concentration of monomers in the bulk solution.
If the event of molecular attachment is controlled by interface transfer, the monomers are in immediate contact with the nucleus but need to make a random jump over a distance d0 ≈ (60/π)1/3 before joining into the nucleus. Assuming that such a jump is proportional to D and the sticking coefficient λ of monomers, j* = DC/d0 and S* = 4πr*2, and f* is given by
f∗=λ(6π2v0)1/3DCn*2/3=λ(6π2v0)1/3Dn*2/3C∗S                      (16) f * = λ ( 6 π 2 v 0 ) 1 / 3 D C n * 2 / 3 = λ ( 6 π 2 v 0 ) 1 / 3 D n * 2 / 3 C * S
The aforementioned molecular interpretations of nucleation kinetics appear plausible and were used to qualitatively explain crystal nucleation phenomena in condensed phases. In some cases, CNT does provide a reasonable prediction on nucleation rate, e.g., the homogeneous nucleation of water droplets in vapors [48][6], but it fails in many other cases wherein the predicted nucleation rate often displays a few orders of magnitude derivation from measurements [49][7]. Even for simple mono-component nucleation in vapor condensation like methanol, the measured nucleation rate is 10−10 slower than the predicted one [50][8]. Several major assumptions of CNT are responsible for these discrepancies: (1) The molecular arrangement of a crystal nucleus is identical to the bulk crystalline phase, and no surface free energy or interface tension difference between the two (the so-called capillarity approximation). This assumption, however, appears incompatible with the Gibbs–Thomson effect in which the curved step displays higher surface tension than that of the straight one. In addition, the surface tension of a crystal nucleus can be also less than that at a flat interface [51[9][10],52], which is valid at least in isobaric supercooling [53,54][11][12]. (2) The evolution of crystalline order and clusters’density occurs simultaneously in crystal nucleation, and growth and dissipation of clusters proceed respectively via the attachment and detachment of monomers (i.e., Szilard–Farkas model). However, it is possible that some organic systems displaying significant molecular association or aggregation form clusters via dimer or oligomers, not only monomers [13,38,55][4][13][14]. Further, the large stable ionic aggregates or clusters were also reported in solution prior to nucleation in inorganic systems [56,57][15][16]. (3) The steady-state nucleation process is assumed, and the stationary distribution of clusters is established instantaneously upon reaching the supersaturation state. In addition, the overestimated rate of crystal nucleation was often attributed to heterogeneous nucleation through foreign particles, which, nevertheless, are not well defined in both structure and concentration. Besides, recent studies have also shown that the discrepancy at high metastability is due to the nucleation times measured in not-fully relaxed liquids [58,59,60][17][18][19].

References

  1. Kelton, K.F.; Frenkel, D. Preface: Special Topic on Nucleation: New Concepts and Discoveries. J. Chem. Phys. 2016, 145, 211501.
  2. Kashchiev, D. Nucleation: Basic Theory with Applications; Butterworth Heinemann: Oxford, UK, 2000.
  3. Tung, H.-H. Crystallization of Organic Compounds: An Industrial Perspective; John Wiley & Sons: Chichester, UK, 2009.
  4. Davey, R.J.; Schroeder, S.L.M.; Ter Horst, J.H. Nucleation of Organic Crystals—A Molecular Perspective. Angew. Chem. Int. Ed. 2013, 52, 2166–2179.
  5. Bai, G.; Gao, D.; Liu, Z.; Zhou, X.; Wang, J. Probing the critical nucleus size for ice formation with graphene oxide nanosheets. Nature 2019, 576, 437–441.
  6. Kashchiev, D. Analysis of experimental data for the nucleation rate of water droplets. J. Chem. Phys. 2006, 125, 044505.
  7. Sharaf, M.A.; Dobbins, R.A. A comparison of measured nucleation rates with the predictions of several theories of homogeneous nucleation. J. Chem. Phys. 1982, 77, 1517–1526.
  8. Strey, R.; Wagner, P.E.; Schmeling, T. Homogeneous nucleation rates for n-alcohol vapors measured in a two-piston expansion chamber. J Chem Phys. 1986, 17.
  9. Schmelzer, J.W.; Abyzov, A.S. Crystallization of glass-forming liquids: Thermodynamic driving force. J. Non-Cryst. Solids 2016, 449, 41–49.
  10. Schmelzer, J.W.P.; Abyzov, A. Crystallization of glass-forming liquids: Specific surface energy. J. Chem. Phys. 2016, 145, 064512.
  11. Espinosa, J.R.; Vega, C.; Valeriani, C.; Sanz, E. Seeding approach to crystal nucleation. J. Chem. Phys. 2016, 144, 034501.
  12. Tipeev, A.O.; Zanotto, E.D.; Rino, J.P. Diffusivity, Interfacial Free Energy, and Crystal Nucleation in a Supercooled Lennard-Jones Liquid. J. Phys. Chem. C 2018, 122, 28884–28894.
  13. Chattopadhyay, S.; Erdemir, D.; Evans, J.M.B.; Ilavsky, J.; Amenitsch, H.; Segre, C.U.; Myerson, A.S. SAXS Study of the Nucleation of Glycine Crystals from a Supersaturated Solution. Cryst. Growth Des. 2005, 5, 523–527.
  14. Gidalevitz, D.; Feidenhans’L, R.; Matlis, S.; Smilgies, D.-M.; Christensen, M.J.; Leiserowitz, L. Monitoring In Situ Growth and Dissolution of Molecular Crystals: Towards Determination of the Growth Units. Angew. Chem. Int. Ed. 1997, 36, 955–959.
  15. Gebauer, D.; Völkel, A.; Cölfen, H. Stable Prenucleation Calcium Carbonate Clusters. Science 2008, 322, 1819–1822.
  16. Myerson, A.S.; Trout, B.L. Nucleation from Solution. Science 2013, 341, 855–856.
  17. Fokin, V.M.; Abyzov, A.S.; Yuritsyn, N.S.; Schmelzer, J.W.; Zanotto, E.D. Effect of structural relaxation on crystal nucleation in glasses. Acta Mater. 2021, 203, 116472.
  18. Rodrigues, L.R.; Abyzov, A.S.; Fokin, V.M.; Schmelzer, J.W.; Zanotto, E.D. Relaxation effect on crystal nucleation in a glass unveiled by experimental, numerical, and analytical approaches. Acta Mater. 2022, 223, 117458.
  19. Xia, X.; Van Hoesen, D.C.; McKenzie, M.E.; Youngman, R.E.; Kelton, K.F. Low-temperature nucleation anomaly in silicate glasses shown to be artifact in a 5BaO·8SiO2 glass. Nat. Commun. 2021, 12, 2026.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
Video Production Service
Feedback