Free Route Airspace

Free Route AirspaceThe acronym (FRA), a new stands for Free Route Airspace. It is an operational concept implemented across that was created to modernize the European airspace, is designed to eliminate the adverse effects of air traffic, reduce fuel consumption, simplify. This modernization is expected to help in reducing fuel consumption, emissions production and to improve flight efficiency; also, to overcome the problems related to the environment and the aviation sectors’ efficiency and capacity. FRA is defined as a specified volume of airspace in which the airspace users can freely plan a route by using the FRA significant points. FRA significant points are published in the national States’ AIP (Aeronautical Information Publications), part ENR 4.1/ ENR 4.4 with a clear reference to FRA and indicating the FRA relevance of the point, see (1). The FRA relevance of the points is important as it specifies the usage of the FRA point. All flights inside the FRA airspace remain subject to air traffic control (ATC) which is the service provided by the ground-based air traffic controllers. Its primary goal is to prevent collisions, organize and expand flight planning. edite the flow of air traffic, and provide information and other support for pilots. Europe is the first region in the world that fully implemented the FRA concept. The first country that introduced full FRA was Portugal (in 2009). So far, FRA has been successfully implemented in the countries of northern, south-east, and central south-east Europe. 

Significant Points and Mathematical Modelling

We can model FRA system by using graph theory, networks and geometry. We work with 2-dimensional space defined by latitude a longitude in the horizontal part of FRA. The airspace is defined by significant points. The significant point is given by GPS coordinates, name, and other attributes, see ^[1] and ^[2]. The FRA significant points, are divided in:

1. FRA Horizontal Entry Point - It is a published significant point located on the horizontal boundary of FRA from which the FRA operations are allowed. It should be located exactly on the boundary of the relevant FRA area. This type of point is displayed with a symbol \Delta (Δ) and black colour in Figure 1.

2. FRA Horizontal Exit Point - It is a published significant point located on the horizontal boundary of FRA to which the FRA operations are allowed. It should be located exactly on the boundary of the relevant FRA area. In Figure 1, this type of point is displayed with a symbol \Delta (Δ) and blue colour.

3. Combined FRA Horizontal Entry and Exit Point - It is a published significant point located on the horizontal boundary of FRA from or to which the FRA operations are allowed. It should be located exactly on the boundary of the relevant FRA area. This type of point is displayed with a symbol \Delta (Δ) and brown colour in Figure 1.

4. FRA Intermediate Points (I) - It is a published or unpublished point defined by geographical coordinates or by bearing and distance via which FRA operations are allowed. The FRA concept includes other type of significant points as well, but these are not necessary for us now. This type of point is displayed with a symbol \ circ (º) in Figure 1. We can also see the different colours. The intermediate points can be used for overflights and/or for arrivals to the airports and/or departures. We needed this detailed division for our calculations, but this is not a part of this description.

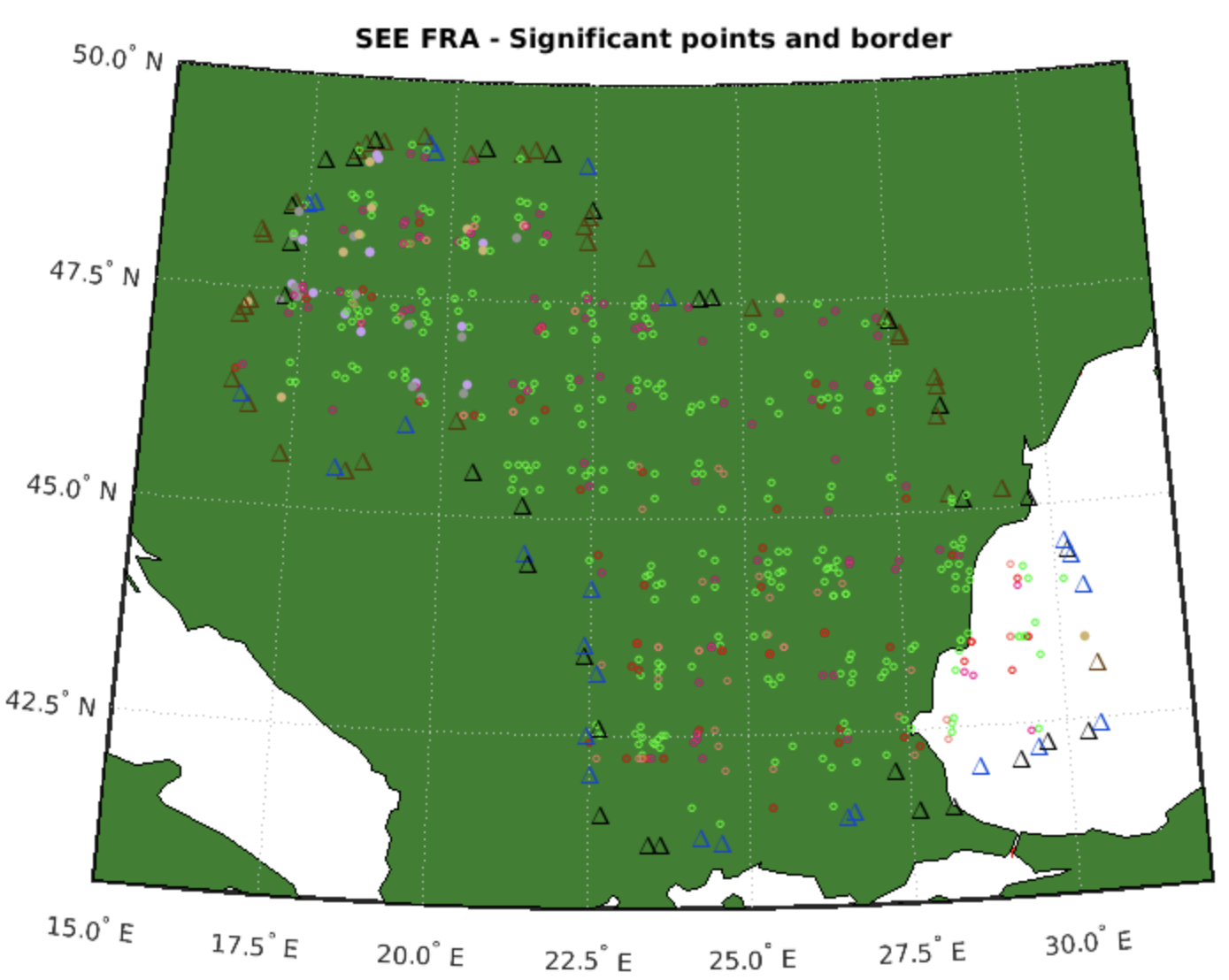Figure 1: Significant Entry, Entry and Exit, and Intermediate points

Simple Polygon

We sought to answer the question of what mathematical object can be used to describe the FRA concept. We found such an object, this object was the simple polygon with vertices Horizontal Entry or Combined Horizontal Entry and Exit points. We define terms polygon and simple polygon before the axiom is determined. The polygon is a two-dimensional closed polyline consisting of a set of line segments (sides or edges) connected such that no two segments cross. The points where two edges meet are the polygon's vertices. The simple polygon is a polygon that does not intersect itself and encloses only one region (polygon is simply connected). 

Spatially Bounded Airspace Axiom

For each airspace V there is a simple polygon

\begin{equation*} B({V})=\left\{ [x_{i},y_{i}];[x_{i},y_{i}]\in {V},i=0,1,\cdots,n,and\;x_{0}=x_{n},y_{0}=y_{n}\right\} \end{equation*}

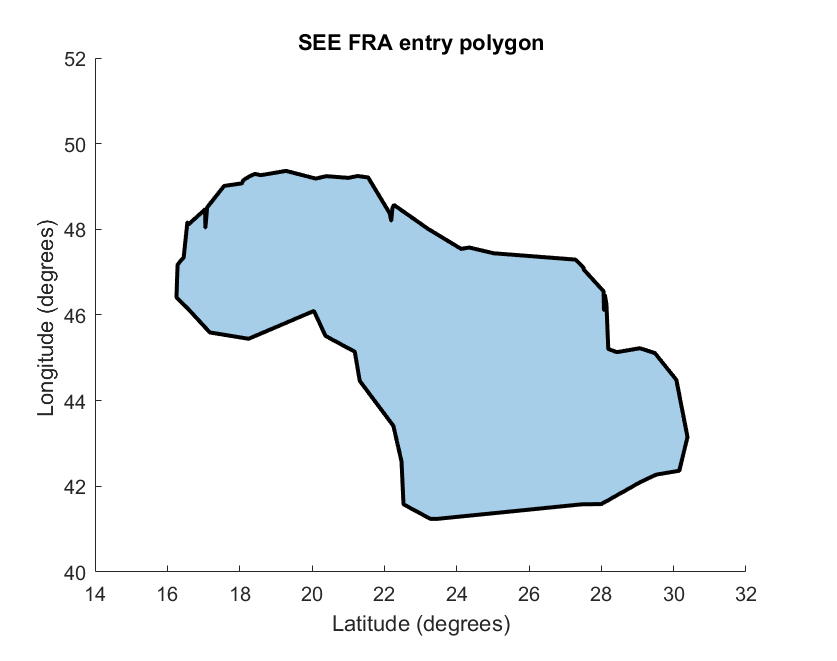Figure 2: SEE FRA airspace polygon

We can see the graph with SEE FRA significant points in

For any set of significant points of airspace it is possible to construct a simple airspace polygon, which means the horizontal boundary of airspace. The airspace polygon exists in the plane (on the 2D map) and on the sphere, on the surface of the Earth. 

We can see the graph with South-East Europe Free Route Airspace (SEE FRA) significant points in

Figure 1. All these points have the coordinates that are expressed by longitude and latitude in a geodetic coordinate system. We identified the axiom that determines an airspace.

. SEE FRA presents an airspace over European states: Slovakia, Hungary, Romania and Bulgaria, in the year 2021. All  SEE FRA significant points have the coordinates that are expressed by longitude and latitude in a geodetic coordinate system. We identified the axiom that determines an airspace.

Each airspace is given by a simple polygon of significant entry or (entry and exit) points.

We can see a polygon for SEE FRA airspace in

We can see the SEE FRA airspace polygon in Figure 2. It is a simple polygon because polygon has only one region and does not intersect itself. Some publications (^[3] also) use the term "no loop" instead of "does not intersect itself". Similarly, instead of "has only one region", "no hole". These terms have the same meaning in different fields of mathematics.

The Figure 1. and

Figure 2, for details see

. was constructed using a MATLAB program, which can be found in the MATLAB File Exchange database, see

^[4]. This polygon defines the horizontal boundary of airspace. The characteristics of this polygon are that it does not contain holes and loops. We were able to formulate and prove all these statements after studying an airspace’s FRA concept and mathematical properties. We have also shown that for any set of significant points of airspace, it is possible to construct a simple airspace polygon.

. The program shows how we can work with maps, significant points, GPS coordinates and airspace polygon in Free Route Airspace.