Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Jason Zhu and Version 1 by Oludamilare Bode Adewuyi.
In recent times, microgrids (MG) have emerged as solution approach to establishing resilient power systems. However, the integration of renewable energy resources (RERs) comes with a high degree of uncertainties due to heavy dependency on weather conditions. Hence, improper modeling of these uncertainties can have adverse effects on the performance of the microgrid operations. Due to this effect, more advanced algorithms need to be explored to create stability in MGs’. The model predictive control (MPC) technique has gained sound recognition due to its flexibility in executing controls and speed of processors.
- Microgrids
- Renewable Energy Resources
- Model Predictive Control
1. Introductino
1. Introduction
Managing the optimal planning of a microgrid is a very difficult task due to the fact that they are small decentralized low voltage systems with small demand and a high rate of disturbances from intense penetration of renewable energy resources (RERs). Model predictive control (MPC) has been applied to both grid-connected and isolated microgrids(MG) systems to help deal with several parameters as seen in Figure 1. Many scholarly works have been done to minimize the operating cost or maximize the revenue generation of microgrids but accurately implementing the mentioned objectives has been difficult due to numerous factors. These factors could be as a result of the intermittency posed by nature (weather conditions), error in trying to predict the situation of nature, and the computational complexities that are associated with optimizing the situation to get an optimal plan. According to [61][1], there are two standard methods or approaches used to solve the problem of uncertainty in MGs: Reactive approach and preventive approach.
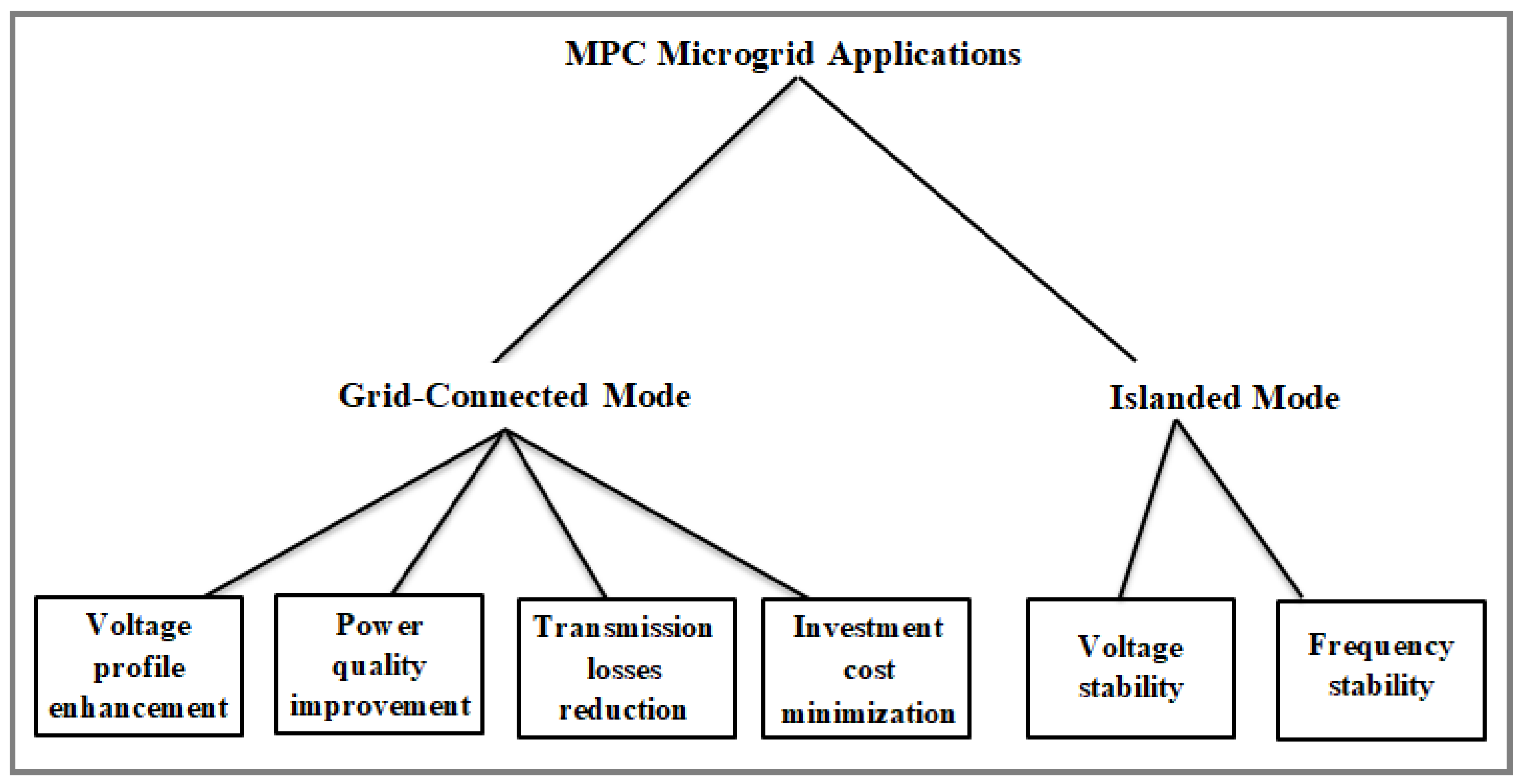
Figure 1. MPC solution approach to MG operations.
The reactive method depends on a priori information or historical or predefined deterministic data (MPC and rolling horizon approaches) and the preventive method depends on scenario generations (stochastic and robust optimizations). Majority of both the reactive and preventive optimization techniques carried out in MGs are centered on grid-connected systems compared to isolated MGs [62][2]. The preventive approaches have proven to be ineffective and not reliable for uncertainty considerations.
The stochastic optimization approach requires assigning probabilities for scenario generations, which is sometimes computationally demanding with the static assumption of uncertainty. The robust optimization becomes over-conservative for measurements and requires different algorithms for different uncertainty sets. This is not the case of MPC; it works on inputs of a system considering the internal dynamics to give or predict an output by capturing forecast error to compensate for unforeseen initial forecasting, making it ideal for uncertainty consideration [63,64,65][3][4][5].
Many times, MPC has been combined with either of the two preventive methods to prevent or reduce uncertainties in many scholarly articles. When MPC is combined with stochastic optimization to give the Stochastic Model Predictive Control (SMPC), the stochastic scenarios are used to execute the optimization process by assigning probabilities without much or totally considering the disturbances in the process. The MPC technique helps to reduce the computational time and takes account of the uncertainties without assuming by implementing a feedback scenario where compensation is done to eradicate the external influences of the integration of renewable technologies.
Thus, combining model predictive control with robust optimization gives a better result compared to robust optimization because instead of employing different algorithms which require time and more expertise, MPC does a single consideration of all the uncertainties or disturbances acting on the system. The optimizer in the MPC algorithm has the ability to trace errors made by the process model in predicting future outputs based on the dynamics of the system. Conservatism is highly reduced by the action of the MPC compensation process.
2. MPC for Grid-Connected MG Applications
More work of MPC applications to MG is centered on grid-connected systems than isolated systems because the cost of implementing measurements, automation, forecasting, and information processing is very small compared with the derived economic benefits as opposed to isolated systems [10][6]. Accuracy of the forecast of load and RERs is of better quality in grid-connected systems. Decentralizing power systems through the establishment of MGs has led to an increase in demand and accessibility of energy but comes with uncertainties of demand and RERs. Barrios et al. proposed an MPC approach for unit commitment in MG in the presence of high uncertainties associated with demand and RESs [66][7]. A particular type of energy market is considered so that the MG can provide the required demand of load and RERs. An MPC technique is applied at every time step to cover demand regarding uncertainties introduced due to prediction. The main objective of the MPC technique adopted in the work is to reduce the operational cost. Two conditions are considered in the study, which is the conventional unit commitment and unit commitment based on MPC. Prediction errors increased the operation cost of the conventional system but a reduced cost is seen for the MPC unit commitment due to the feedback mechanism. Parisio et al. proposed that the decentralization of the power system has led to an increase in energy demand and therefore requires new methodologies to model a smart grid environment [67][8]. The work is focused on minimizing overall MG operational costs to match predicted demand for a certain day by obeying the complex constraints. Four different strategies are considered, which are heuristics, Mixed-Integer Linear Programming (MILP), MILP-MPC, and benchmark. It is supposed that the demand for load and RERs are known with certainty. The proposed MILP-MPC gives less violation because of the feedback mechanism introduced by the MPC, giving a result closed to the benchmark. Xie and IIic proposed an MPC algorithm to dispatch all the available resources to supply fluctuating loads at a minimum cost due to consideration of the prediction model [68][9]. The output of the controllable units is adjusted to compensate for uncertainties. Kou et al. [69][10] proposed a Stochastic Model Predictive Control (SMPC) approach that works in a two-layer step. The top layer ensures that there is a balance of power in the system and the bottom layer considers the uncertainties emerging from both supply and demand ends. The main objective of the proposed approach is to ensure optimal power scheduling with total consideration of disturbances acting on the system. The special attribute associated with this proposed approach is the consideration of all uncertainties from both demand and supply sides. The uncertainties from wind generation and PEV charging both have different distribution characteristics but the MPC controller in the system handles both uncertainties simultaneously instead of treating them as separate uncertainty sets. Despite MPC’s ability to compensate for disturbances in the RERs system, some violations have been experienced in scheduling optimal resources. In order to mitigate, these violations, forecasting errors have to be taken into consideration. Y. Zhang et al. proposed an MPC approach, considering forecasting uncertainties and forecast errors of load, wind, PV, and electricity price [70][11]. The work incorporated stochastic analysis where scenarios are generated to approximate forecast errors and uncertainties. The objective is to minimize operation costs. Three different states of the art approaches are compared to the proposed stochastic MPC; a Deterministic Day Ahead programming (D-DA), a Stochastic Day Ahead programming (S-DA), and Deterministic Standard MPC (D-MPC). Simulation results show that S-MPC yields the lowest cost compared to D-MPC. This is because both S-DA and D-DA are open-loop systems where optimization takes place only at the beginning of the scheduling. Both D-MPC and S-MPC are closed-loop where optimization is executed once for each time step. S-MPC considers all uncertainties affecting the system while D-MPC assumes that the system is stable with known demand and no disturbance. Gulin et al. proposed an approach of a power flow optimization in a Direct Current (DC) MG that accounts for predictions uncertainty [71][12]. Unlike other methods of uncertainty consideration, here a chance-constrained method is used to account for power prediction uncertainties. The work is done on the idea of allowing violations of constraints in line with predefined probability levels, allowing the utility grid to compensate for error(s) on the prediction horizon. Two different approaches are used to deliver a minimum cost; D-MPC and S-MPC. D-MPC did not account for uncertainties while S-MPC accounted for uncertainties and gives a lower cost by allowing a tradeoff between constraints being violated and prospect. Dao et al. proposed a hierarchical and distributed MPC approach for the energy management of a microgrid. The main objective of the proposed approach is to provide an economic management framework to maximize the benefits of the system. In order to ensure that forecast errors are taken into consideration and that uncertainties are effectively and efficiently handled to enhance maximum benefits, a negotiation activity or process is carried out between the hierarchical and distributed MPC algorithms to compensate for forecast errors within the system [72][13]. Gambino et al. proposed an economic dispatch problem for an integrated microgrid (heat and electricity generation). The main objective of the proposed approach is to optimally dispatch resources so as to minimize the overall cost of the microgrid. Microgrids that normally incorporate dual derivatives, as the case of combined heat and power to solve economic dispatch problems, are prone to uncertainties from loads, energy prices, and weather forecasts. A feedback mechanism generated by the MPC controller compensates for uncertainties associated with time-varying loads, energy prices, and RERs power outputs [73][14]. Bella et al. proposed a hierarchical MPC (two-layer control system) control scheme that constitutes of dynamic decoupled subsystems. The main objective of the approach is to optimally share resources among the various subsystems so as to satisfy the overall demand and account for disturbances acting on the system [74][15]. Scheduling takes place in the upper layer and each subsystem is adjusted or designed in a way that at any time instance, an independent control action can be executed from the internal request or a neighboring subsystem based on the MPC. At the end of every time step, the supervisor checks the system for either a deficit or excess demand in each subsystem. A compensation activity is initiated by the supervisor in the subsystem(s) that exhibit shortages due to disturbances or uncertainties so as to ensure the overall system demand is achieved. The majority of researchers have focused on exogenous factors or external factors (customer loads, wind speed, PV, and price profile) in considering uncertainty measurements with few works or no work being done considering endogenous factors (types of equipment, and storage). Prodan and Zio proposed a predictive control framework that takes into account uncertainties modeling. The work is focused on including internal (state) dynamics and structural properties of the individual components of RESs (solar and wind, on-site storage) which may change (stochastically) due to degradation, failure, and aging effects. By considering both factors, the operating cost of the system can be reduced [75][16]. Nassouron et al. proposed an MPC approach for an economic dispatch problem considering heterogeneous systems (system with different computational applications) [76][17]. Owning to the fact that several heterogeneous generators and storage elements are used in the approach, the dispatch problem cannot be solved using classical optimization methods due to the differences in characteristics of the generators and storage elements. Two techniques are used to optimally schedule the resources: MPC tracking and Economic MPC (EMPC). The Economic MPC yields a better cost compared to the tracking MPC.3. MPC for Isolated MG Applications
Many utility companies and government-sponsored electric power systems have been implementing or providing incentives or demand-side management opportunities for their customers to establish on-site Distributed Generators (DGs) and energy storage systems to increase the number of isolated MGs in the supply of power. However, these efforts have proven to be quite expensive or not cost-effective at all. Hence, several research efforts have been devoted and are continuously being devoted to achieving the cost-effective operation of the isolated microgrid. Parissio et al. proposed an MPC approach for energy management of multiple residential MGs having DERs, electrical storage systems with both thermal, and electrical loads [92][18]. The objective of the proposed MPC approach is to reduce energy costs and improve customers’ comfort through a demand-side management scheme. An optimal plan is computed to compensate for imbalances affecting the system based on the weather forecast. The demand-side management scheme can help customers to know when to have an affordable cost of uninterruptable power. Most of the works in predictive algorithms have considered favorable conditions (where generation is greater than demand). According to [93][19], a nonlinear MPC algorithm is developed or proposed for an Energy Management System (EMS) of an isolated MG with DERs in which automated load shedding of non-critical loads is done when the system foresees power imbalances that could affect the stability of the MG. This predictive algorithm is proposed to identify upcoming generation problems when MG is operating in an islanded mode. The objective is to predict and manage constraints in states and control signals. Hans et al. proposed a control technique that can give better prediction accuracy while minimizing cost. Comparison is presented between an open-loop minimax approach and closed-loop minimax MPC approach considering the worst-case cost evaluation in trying to get better prediction accuracy and uncertainty handling [94][20]. The open-loop system gives a very conservative solution because it did not implement a feedback mechanism. The closed-loop Minimax MPC strategy however employed the theory of paramterization (choosing parameters) of future inputs on the predicted disturbance leading to accurate predictions and lower cost. This is due to the presence of the MPC strategy that normally uses a predefined input to make accurate future predictions. Gu et al., proposed an MPC technique for Combined Cooling, Heat, and Power microgrid (CCHP) with feedback correction to reduce running cost and handle uncertainties [95][21]. A two-stage optimization approach is executed in this work oof which the first stage is based on forecasting the required load and renewable energies integration. The second stage focuses on compensating for the error in the prediction process. The MPC ensures that forecast is repeated for every time interval to get accurate data to be in line with rapid changes that take place in load and RERs demand. If, however, there is a disturbance in the system due to inaccurate forecasting, a feedback correction is done to eliminate the disturbance. Deterministic unit commitments have proven inappropriate for island MGs because their small scale demands are hard to predict and RERs generation is highly variable. Y. Zhang et al., proposed a Robust Model Predictive Control (RMPC) approach to solve the operating cost of an islanded MG by minimizing cost [57][22]. The work states that of recent times, both chance-constrained and scenario-based stochastic optimization methods have been used to minimize MG cost. It has however, been concluded that these two methods involve high or huge computational burden and uncertain parameters and forecast errors are not accurately accounted for and as a result, have posed a high negative impact on MG cost. However, another method is the robust optimization used to solve an optimal scheduling problem with uncertain parameters. The conservativeness of this approach is a huge concern for cost minimization by MG operators. In this proposed RMPC approach, an MPC is introduced to reduce the conservativeness of the RO due to the rolling up manner and feedback mechanism that it exhibits. Two control strategies are considered in the approach used; a conventional 2-stage RO and RMPC-based optimization. The results for the cost function of RMPC is lower than the conventional two-stage RO since a feedback control action is generated to consider the forecast uncertainties. Sach et al. proposed a stochastic model predictive control approach for a rural isolated microgrid. The main focus or objective of the proposition is the development of an advanced control technique to improve robustness towards predictions error and uncertainties acting on the system. For normal MPC operation, a control technique is implemented for a one-time step and subsequent control actions rely on the dignity of the previous time step [96][23]. This proposed stochastic MPC considers the probability of a constraint violation over several time steps. A probability distribution approach based on the stochasticity of the load and renewables is used to compensate for the disturbances on the system. Jaboulay et al. proposed a controlled algorithm based on MPC with the objective of minimizing operation cost and maintaining power balance in the system [97][24]. The controller takes into account the physical constraints of the system while scheduling the required resources. Instead of making a few decisions as opposed to other control techniques for every time step, the MPC takes multiple decisions for every updated forecast because it can handle multiple inputs and outputs. Scenarios are run in parallel on a semi-physical platform to compensate for uncertainties. According to [10][6], the cost of forecast service and power quality using automation is very high in isolated systems compared to grid-connected systems. Zhang et al. proposed an EMS for multi-isolated MGs connected by a centralized system to minimize the overall cost of the EMS [47][25]. An MPC technique is introduced with the intent of considering or reducing the impacts of forecast errors of the load and RERs, hence reducing overall cost. Berkel et al. proposed a hierarchical MPC for a smart MG to solve the power stability issue. Two (2) levels of management are presented where the first level solves the frequency issue and the second level solves the cost function. The objective of the hierarchical MPC is to make accurate predictions of load and RERs by rejecting disturbances from penetration and to handle constraints to guarantee stability and performance of the smart MG [9][26].References
- Silvente, J.; Kopanos, G.M.; Dua, V.; Papageorgiou, L.G. A rolling horizon approach for optimal management of microgrids under stochastic uncertainty. Chem. Eng. Res. Des. 2018, 131, 293–317, Energy Systems Engineering.
- Farrokhabadi, M.; Cañizares, C.A.; Bhattacharya, K. Unit Commitment for Isolated Microgrids Considering Frequency Control. IEEE Trans. Smart Grid 2018, 9, 3270–3280.
- Zhang, Y.; Fu, L.; Zhu, W.; Bao, X.; Liu, C. Robust model predictive control for optimal energy management of island microgrids with uncertainties. Energy 2018, 164, 1229–1241.
- Kachhap, S.; Mohanta, D.K.; Jha, R.C. Reliabilty evaluation of microgrid scheduling. In Proceedings of the 2017 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 17–18 March 2017; pp. 1–6.
- Hu, W.; Wang, P.; Gooi, H.B. Toward Optimal Energy Management of Microgrids via Robust Two-Stage Optimization. IEEE Trans. Smart Grid 2018, 9, 1161–1174.
- Mazzola, S.; Vergara, C.; Astolfi, M.; Li, V.; Perez-Arriaga, I.; Macchi, E. Assessing the value of forecast-based dispatch in the operation of off-grid rural microgrids. Renew. Energy 2017, 108, 116–125.
- Barrios, L.A.; Valerino, J.B.; Nozal, R.; Escaño, J.M.; Martínez-Ramos, J.L.; Gonzalez-Longatt, F. Stochastic Unit Commitment in Microgrids based on Model Predictive Control. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies (SEST), Seville, Spain, 10–12 September 2018; pp. 1–5.
- Parisio, A.; Rikos, E.; Glielmo, L. A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827.
- Xie, L.; Ilic, M.D. Model predictive dispatch in electric energy systems with intermittent resources. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 42–47.
- Kou, P.; Feng, Y.; Liang, D.; Gao, L. A model predictive control approach for matching uncertain wind generation with PEV charging demand in a microgrid. Int. J. Electr. Power Energy Syst. 2019, 105, 488–499.
- Zhang, Y.; Zhang, T.; Wang, R.; Liu, Y.; Guo, B.; Zhang, T. Dynamic dispatch of isolated neighboring multi-microgrids based on model predictive control. In Proceedings of the 2016 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Chengdu, China, 19–22 October 2016; pp. 50–55.
- Gulin, M.; Matuško, J.; Vašak, M. Stochastic model predictive control for optimal economic operation of a residential DC microgrid. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 505–510.
- Dao, L.A.; Dehghani-Pilehvarani, A.; Markou, A.; Ferrarini, L. A hierarchical distributed predictive control approach for microgrids energy management. Sustain. Cities Soc. 2019, 48, 101536.
- Gambino, G.; Verrilli, F.; Meola, D.; Himanka, M.; Palmieri, G.; Vecchio, C.D.; Glielmo, L. Model predictive control for optimization of combined heat and electric power microgrid. IFAC Proc. Vol. 2014, 47, 2201–2206.
- Bella, A.L.; Bonassi, F.; Farina, M.; Scattolini, R. Two-layer model predictive control of systems with independent dynamics and shared control resources. IFAC-PapersOnLine 2019, 52, 96–101.
- Prodan, I.; Zio, E. A model predictive control framework for reliable microgrid energy management. Int. J. Electr. Power Energy Syst. 2014, 61, 399–409.
- Nassourou, M.; Puig, V.; Blesa, J.; Ocampo-Martinez, C. Economic model predictive control for energy dispatch of a smart micro-grid system. In Proceedings of the 2017 4th International Conference on Control, Decision and Information Technologies (CoDIT), Barcelona, Spain, 5–7 April 2017; pp. 0944–0949.
- Parisio, A.; Wiezorek, C.; Kyntäjä, T.; Elo, J.; Johansson, K.H. An MPC-based Energy Management System for multiple residential microgrids. In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 7–14.
- Minchala-Avila, L.I.; Garza-Castañón, L.; Zhang, Y.; Ferrer, H.J.A. Optimal Energy Management for Stable Operation of an Islanded Microgrid. IEEE Trans. Ind. Inform. 2016, 12, 1361–1370.
- Hans, C.A.; Nenchev, V.; Raisch, J.; Reincke-Collon, C. Approximate closed-loop minimax model predictive operation control of microgrids. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 241–246.
- Gu, W.; Wang, Z.; Wu, Z.; Luo, Z.; Tang, Y.; Wang, J. An Online Optimal Dispatch Schedule for CCHP Microgrids Based on Model Predictive Control. IEEE Trans. Smart Grid 2017, 8, 2332–2342.
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31.
- Sachs, J.; Gienger, A.; Sawodny, O. Combined probabilistic and set-based uncertainties for a stochastic model predictive control of island energy systems. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 6767–6772.
- Jaboulay, P.; Zhu, W.; Niu, X.; Pan, X.; Gao, S. Real-Time Energy Management Optimization Using Model Predictive Control on a Microgrid Demonstrator. In Proceedings of the 2017 IEEE International Conference on Energy Internet (ICEI), Beijing, China, 17–21 April 2017; pp. 226–231.
- Wen, S.; Xiong, W.; Cao, J.; Qiu, J. MPC-based frequency control strategy with a dynamic energy interaction scheme for the grid-connected microgrid system. J. Frankl. Inst. 2020, 357, 2736–2751.
- Berkel, F.; Görges, D.; Liu, S. Load-frequency control, economic dispatch and unit commitment in smart microgrids based on hierarchical model predictive control. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 2326–2333.
More
