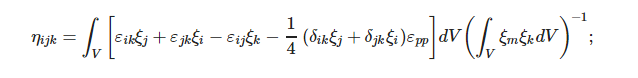SGTs are featured with the introduction of one or more scale lengths in the model used to describe the medium behavior. Among all the SGTs, those that make use of the gradient of the plastic part of the strain are called Strain Gradient Plasticity Theories (SGPT).
- Strain Gradient
- Machining Simulation
- Strain Gradient Plasticity
- Micromorphic medium
Note:All the information in this draft can be edited by authors. And the entry will be online only after authors edit and submit it.
1. Introduction
The topic of Strain Gradient Theories (SGT) experienced a fervent increase of interest from the scientific community in recent years. Although multiple reasons made the SGT one of the hot topics in the field of Continuum Mechanics (CM), the main causes can be identified in the ever-increasing computational power of numerical calculators (thus enabling the implementation of techniques beforehand impossible to use) and in the demand of more sophisticated CM theories which would better predict the medium behavior under specific material deformation conditions. SGTs could be employed whenever the Classical CM framework is not delivering anymore a proper medium behavior description if compared with experimental observations. The features embodied in the SGTs can be of crucial importance in several situations, and in this manuscript we assess the role that they might play for manufacturing process simulations. However, it must be noted that the adoption of such theories increases the computational cost involved in simulating the observed phenomenon.
The most general feature, shared by all the SGTs, is the introduction of one or more scale lengths in the model used to describe the medium behavior. This is done through the definition of additional deformation measures that are meant to capture specific phenomena which cannot be predicted by the classical CM models. In the vast majority of the cases, the magnitude and the influence of these additional deformation measures are negligible if compared with the standard one, i.e., strain. In specific situations, however, the material behavior demonstrates noticeable susceptibility to these supplementary deformation measures, and proper models are required to capture such behaviors through simulations. The gradient of the strain has been widely and unanimously recognized as one of the main feature which needs to be incorporated in the Classical CM theory to predict such behaviors. Among all the SGTs, those that make use of the gradient of the plastic part of the strain are called Strain Gradient Plasticity Theories (SGPT).
2. Reported Applications of SGPTs in Manufacturing Processes Simulation
The implementation of a SGPT in a FEM solver is not an easy task, and the more complex the model, the more difficult is the implementation. Furthermore, if the SGPT has to be applied to machining simulation, this represents an additional element of difficulty due to the additional features that must be taken care of, such as friction, temperature and strain rate influence, large deformation framework and so on.
From the point of view of FE implementation, two groups of SGPT can be delineated: one that only requires to access and enhance the material behavior of the Finite Elements, and another one that requires a deeper level of accessibility. For the latter, a total new Element formulation must be provided. The key feature to differentiate between the two groups is the necessity of defining new degrees of freedom for the element. Whether it is demanded to add another degree of freedom or not, it depends on the nature of the continuum description that must be used: if the strain gradient needs to be evaluated through solution of PDEs, then the variable carrying the strain gradient measure requires to be treated as an additional degree of freedom, otherwise, the strain gradient will be treated as a solution-dependent variable. In the latter case, the strain gradient depends on the displacement field on a similar way the classical strain measure does, and the classical structure of the continuum description is unaltered.
Among the SGT previously presented, the CMSGT is the only one that does not require modifications of the element formulation. This traduces in a easier implementation of the theory, and this represent an advantage that should not be superficially neglected, especially if combined with the already mentioned difficulties characterizing machining simulations. Nonetheless, on a similar low-order theory developed by Acharya and Bassani [109][1] and Bassani [110][2], doubts have been raised on the physicality of the obtained response and on the well-posedness of the boundary value problem.
2.1. Scalar SGPT Applied to Flat Punch Molding
The first example of applications of SGPT in manufacturing operations is the one provided by Guha et al. [111][3]. They implemented the Fleck1997 SGPT as revisited by Fleck and Hutching in 2001 (ref. Section 3.4) in a viscoplastic isothermal large deformation framework to simulate flat punch molding. This manufacturing process is similar to the indentation test in case the size of the surface of the punch is comparable to the material grain size, thus achieving similar deformation fields to the ones developed during an indentation test. This test is of particular interest for manufacturing processes acting at macroscale (≈μm).
2.2. SGPT Used to Model Rolling at Small Scale
The employment of the full gradient of plastic strain for manufacturing operations is reported in a recent contribution by Nielsen et al. [113][4]. They used the SGPT described by Gudmunson [81][5] first, and Fleck and Willis [114] [6] later, to simulate rolling processes of metal sheets of up to 5 μm of thickness in 2D. Simulations were performed under steady-state condition, integrations were done with forward Euler scheme, and the continuum was enhanced with nine additional degrees of freedom, being the components of the plastic strain tensor. Gaussian integration schemes were used for integration over the element. The contact between the plate and the roll was modeled through a sticking-sliding model. The material hardening was set to be dependent on the strain gradient.
Rolling simulations were carried out using different ratios of the characteristic length over the sheet thickness, and the results replicated the experimental values accurately. The simulated rolling force demonstrated sensitivity over the size-effect, similarly to what was experienced experimentally. The authors outlined that large size-effects were measured when the characteristic length over thickness ratio was 0.25.
2.3. MSGT Applied to Orthogonal Cutting
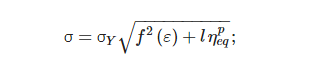 (2)
(2)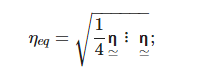
The first line of research here reported is the one originated from Liu et al. [8,115,116][7][8][9]. They implemented the Mix-Gao MSGT, thereby adopting a non-local Taylor-derived material hardening description as in Equation (341), where the equivalent measure of the strain gradient was evaluated as in Equation (332), and they used a non-local volume integral to evaluate the strain gradient at every integration point as proposed by Gao and Huang [117][10]:
where ξi is the i-th local coordinate over which integration is performed. In this framework, the classical continuum mechanics description stays the same, and the strain gradient effects only the plastic flow, acting as an additional source of hardening (this is after all the reasoning behind the MSTG). The flow stress they used is the one in Equation (34), and they used the Johnson–Cook evolution of the flow stress to replace f [118]. The characteristic length was identified with:
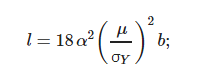
They implemented this model in a Finite Element Procedure, using ABAQUS® Implicit through a UMAT FORTRAN subroutine, and they used this model to study the effect of the radius of the cutting tool during orthogonal micro-cutting [8][7], and to verify the increments in material hardening and cutting energy by using the SGPT [116][9]. They used a sticking-sliding friction model as the one developed by Zorev [70][12]. The thermal fields during simulations have been solved through the classical heat equation. Heat was assumed to generate at the tool-workpiece contact location due to friction and at the plastic zones due to plastic work; the Taylor–Quinney constant was set to 0.9 (90% of the plastic work would transform into heat) [119][13]. An adaptive remeshing algorithm was used to obtain chip separation. The minimum mesh size they used measured 0.06 μm in the cutting zone, with a chip thickness of 0.5 μm.
The work of Liu et al. represents a big contribution toward the application of SGPTs for machining simulation, both in terms of progress toward the objective and in terms of proof of the fact that SGPT are necessary to achieve it. However, the disadvantages of using a MSGT are that the system of PDE describing the continuum behavior have not been rigorously derived and thermodynamical consistency of the model has not been proved, therefore, for future development, a more complete and rigorous SGPT would be ideally used, or a thermodynamically-consistent MSGT would have be provided.
2.4. Micromorphic Media Applied to Forming
The discussed Micromorphic theory is enhancing the medium by nine additional degrees of freedom, this being an equivalent deformation tensor of the microstructure defined at each point of the continuum. It has also been said that the Micropolar and the Microstrain theories are nothing but a constrained version of the Micromorphic theory. Due to the physics that Eringen described with the Micromorphic theory, this terminology associates to the introduction of additional degrees of freedom in the system that are connected with the microstructure. Through the years, many theories that enhance the continuum with additional degrees of freedom have been semantically linked with the Micromorphic theory, although the physics they described was not related to microstructure. However, in the literature, this became an established nomenclature for continuum mechanics theories enhancing the media with additional degrees of freedom.
The additional degree of freedom can be used for different purposes, it can be used for carrying an equivalent measure of the cumulative plastic strain [62,106,107,108] [14][15][16][17] or for an equivalent damage variable [59,64][18][19]. In any case, the equation governing the angular momentum (that for classical continuum mechanics ensures the symmetry of the Cauchy stress tensor) transforms into a balance equation for the additional degrees of freedom and it is referred to as generalized balance equation. In case these additional variables are meant to replace already existing variables, the generalized balance equation transforms into a coupling equation between additional and already existing variables.
3. Conclusions
For the simulation of machining operations that involve the development of high temperatures, regardless of the choice between higher order or higher degree, it is require the adoption of a theory incorporating a thermodynamical description that would ensures a proper thermodynamically-consistent description. The suggested approach would be to define the dissipation potential and the Helmholtz free energy from which the constitutive behavior of the medium would directly follow. If higher temperatures are foreseen, the dissipation potential assumes a fundamental role in determining the material response, thereby a proper calibration of the potential at operational conditions is required. If extremely high temperature develops, e.g., through the friction stir welding technique, melting temperature is likely to occur, and the solid description of the medium is not adequate anymore, since the continuum behaves as liquid rather than solid, therefore a mixed Lagrangian-Eulerian formulation is required to performed the simulation.
One of the main drawback of the majority of the higher order theories is that, since the plastic strain is an additional variable of the system, the boundary conditions in terms of plastic strain must be applied at the moving elasto-plastic boundary, so another additional step is required to identify this boundary inside the original domain. Furthermore, if the simulated manufacturing technique involves the development of plastic strain at the domain boundaries, e.g., orthogonal cutting, then the choice related to the type of boundary conditions (in terms of plastic strain) that must be applied at this boundary is very important. If, however, the process that must be simulated does not involve the production of plastic strain at the boundary, then this question does not need to be posed, and the choice of using this type of continuum theory is not unfavorable. Two simulations of orthogonal cutting using SGPTs were reported, and both of them are using MSGT. In light of the previous discussion, the choice of the MSGT is a smart solution, since it has already been mentioned that this type of SGPT does not require the plastic strain field to be solved through PDEs, therefore it is not characterized by this type of problem.
To conclude, the choice of the SGPT to be adopted for simulations of manufacturing operations must be taken while looking at several characteristic of the observed phenomena occurring during the process:
-
The forces/moments used to shear/shape the continuum localize in areas that are comparable to the grain size of the metal; in this case a further hardening due to the dislocations movement must be properly captured by adopting a SGPT;
-
The velocity with which the continuum is deformed might induce material to behave viscously, and this must be covered by a proper design of the material behavior;
-
The temperature developed during the process might be relatively high, and this imposes to considerate the thermal behavior (often adiabatic) that are taken into account by the definition of a thermodynamically-consistent description of the continuum;
-
Implementation-wise if the plastic deformation is expected to occur at the boundaries, a higher degree theory is favorable.
References
- Acharya, A.; Bassani, J.L. On Non-Local Flow Theories that Preserve the Classical Structure of Incremental Boundary Value Problems. In IUTAM Symposium on Micromechanics of Plasticity and Damage of Multiphase Materials. Solid Mechanics and its Applications; Springer: Dordrecht, The Netherlands, 1996.
- Bassani, J.L. Incompatibility and a simple gradient theory of plasticity. J. Mech. Phys. Solids 2001, 49, 1983–1996.
- Guha, S.; Sangal, S.; Basu, S. Numerical investigations of flat punch molding using a higher order strain gradient plasticity theory. Int. J. Mater. Form. 2014, 7, 459–467.
- Nielsen, K.L.; Niordson, C.F.; Hutchinson, J.W. Rolling at small scales. J. Manuf. Sci. Eng. Trans. ASME 2016, 138, 1–10.
- Gudmundson, P. A unified treatment of strain gradient plasticity. J. Mech. Phys. Solids 2004, 52, 1379–1406.
- Fleck, N.A.; Willis, J.R. A mathematical basis for strain-gradient plasticity theory. Part II: Tensorial plastic multiplier. J. Mech. Phys. Solids 2009, 57, 1045–1057.
- Liu, K.; Melkote, S.N. Finite element analysis of the influence of tool edge radius on size effect in orthogonal micro-cutting process. Int. J. Mech. Sci. 2007, 49, 650–660.
- Liu, K. Process Modeling of Micro-Cutting Including Strain Gradient Effects. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, December 2005.
- Liu, K.; Melkote, S.N. Material strengthening mechanisms and their contribution to size effect in micro-cutting. J. Manuf. Sci. Eng. Trans. ASME 2006, 128, 730–738.
- Gao, H.; Huang, Y. Taylor-based nonlocal theory of plasticity. Int. J. Solids Struct. 2001, 38, 2615–2637.
- Johnson, G.R.; Cook, W.H. A constitutive model and data from metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547.
- Zorev, N. Inter-relationship between shear processes occurring along tool face and shear plane in metal cutting. Int. Res. Prod. Eng. 1963, 49, 143–152.
- Taylor, G.I.; Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. A Math. Eng. Sci. 1934, 143, 307–326.
- Mazière, M.; Forest, S. Strain gradient plasticity modeling and finite element simulation of Lüders band formation and propagation. Contin. Mech. Thermodyn. 2013, 27, 83–104.
- Anand, L.; Aslan, O.; Chester, S.A. A large-deformation gradient theory for elastic-plastic materials: Strain softening and regularization of shear bands. Int. J. Plast. 2012, 30–31, 116–143.
- Poh, L.H.; Peerlings, R.H.J.; Geers, M.G.D.; Swaddiwudhipong, S. An implicit tensorial gradient plasticity model - Formulation and comparison with a scalar gradient model. Int. J. Solids Struct. 2011, 48, 2595–2604.
- Peerlings, R.H.J. On the role of moving elastic-plastic boundaries in strain gradient plasticity. Model. Simul. Mater. Sci. Eng. 2007, 15.
- Saanouni, K.; Hamed, M. Micromorphic approach for finite gradient-elastoplasticity fully coupled with ductile damage: Formulation and computational aspects. Int. J. Solids Struct. 2013, 50, 2289–2309.
- Forest, S. Micromorphic Approach for Gradient Elasticity, Viscoplasticity, and Damage. J. Eng. Mech. 2009, 135, 117–131.